Orthogonal frequency division multiplexing (OFDM) is a predominant transmission technology for ubiquitous wireless broadband networks because it can mitigate severe effects of frequency selective fading and provide good spectrum efficiency [1-4]. There have been many attempts to apply the multiple-input multiple-output (MIMO) technology to OFDM transmission systems, such as [5,6].
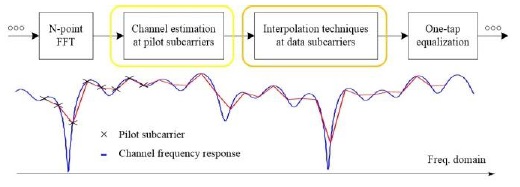
For coherent detection of the received data symbols in OFDM transmission, channel frequency responses (CFRs) must be estimated and equalized. One of the OFDM channel estimation methods is pilot-aided channel estimation (PACE) where pilot symbols are assigned to pilot subcarriers, which are multiplexed with data subcarriers, and channel estimation for data symbols is performed by interpolation techniques. There are three basic factors affecting the performance of the PACE method. These are pilot patterns, estimation methods, and signal detection. The choice of these factors depends on OFDM system specifications and wireless channel conditions.
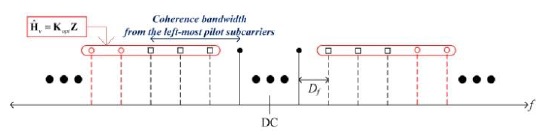
In PACE, CFRs at pilot subcarriers are estimated using least squares (LS) or minimum mean square error (MMSE) estimators, and then, interpolation techniques are performed in order to estimate CFRs at data subcarriers by using the estimated CFRs at pilot subcarriers, as shown in Fig. 1. As an interpolation technique of PACE methods, discrete Fourier transform (DFT)-based interpolation is often used. However, it may have the leakage problem caused by virtual carriers in an OFDM symbol. In order to deal with the leakage problem, some suppression methods were proposed in [7-11]. In particular, optimal and suboptimal linear estimators were proposed to estimate the equally spaced virtual carriers in [11], but whose performances are very sensitive to the coherence bandwidth of wireless channels. Therefore, in this study, optimal and suboptimal linear estimators are reviewed and theoretically analyzed in terms of coherence bandwidth.
The rest of this paper is organized as follows: in Section II, DFT-based channel estimation and its leakage problem are described. Section III reviews optimal and suboptimal linear estimators and analyzes the effect of coherence bandwidth on them. In Section IV, numerical results are presented to show the performance degradation due to the effect of coherence bandwidth. Conclusions are presented in Section V.
>
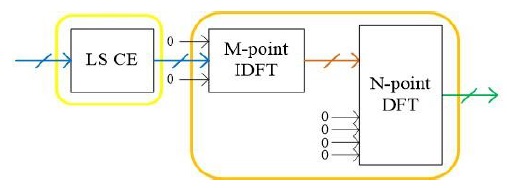
A. DFT-Based Channel Estimation
DFT-based interpolation is an efficient interpolation technique because of its good performance and low complexity [8,9]. The PACE method using DFT-based interpolation is called DFT-based channel estimation, as shown in Fig. 2, where an inverse DFT (IDFT) operation is executed first to obtain the estimated channel impulse responses (CIRs) by using the LS-estimated CFRs at pilot subcarriers, and then, the estimated CIRs are transformed back into the frequency domain by the DFT operation to obtain the final CFRs at data subcarriers.
>
B. Virtual Carriers and Leakage Problem
In most commercialized OFDM systems, virtual carriers are exploited to ease the implementation of spectral masking filters and ensure guard bands to avoid interferences between adjacent systems [10].
However, these virtual carriers have a bad influence on the performance of DFT-based channel estimation. In other words, they may cause leakage effects. Virtual carriers correspond to rectangular windowing in the frequency domain, which results in the convolution of CIRs with the sinc function in the time domain. Hence, the channel taps of CIRs are leaked to one another. Further, time-domain windowing is performed to reduce the noise and interference, which causes spectral leakage or Gibbs phenomenon, as shown in Fig. 3.
In order to review the performance of DFT-based channel estimation and the leakage problem from virtual carriers, the normalized mean square error (NMSE) is represented as follows: Let the number of total subcarriers be
where
where
where
The received pilot vector with entries
where X is a diagonal matrix with
where 0 ≤
where the noise vector is statistically equivalent to W since
where is an
where = −
Then, the DFT operation transforms into the estimated CFR vector in (10)
where =
where −
where U = F
where
where the first term denotes the noise effects and the second term denotes the leakage effects.
III. EFFECT OF COHERENCE BANDWIDTH ON LEAKAGE SUPPRESSION METHODS
>
A. Review of Leakage Suppression Methods
In order to minimize the NMSE in (14), optimal and suboptimal linear estimators were proposed in [11]. They can be expressed as
Then, optimal or suboptimal linear estimators are used to estimate = K
where V
Finally, their NMSEs are given by
From (21) and (22), we find that the NMSE performance improvement depends on the second terms V
>
B. Effect of Coherence Bandwidth
Although optimal and suboptimal linear estimators provide good performance with moderate complexity, their performance may decrease according to wireless channel conditions such as coherence bandwidth.
Coherence bandwidth is a statistical measurement of the range of frequencies over which the channel can be considered flat [12]. The coherence bandwidth can be approximately defined as
where
where we assume
Therefore, if optimal and suboptimal linear estimators try to estimate CFRs outside the range of the coherence bandwidth, they may experience a decrease in their performance.
Computer simulations have been run to analyze leakage suppression methods such as optimal and suboptimal linear estimators in terms of the coherence bandwidth of wireless channels. We consider the OFDM system using QPSK modulation in the 1.25-MHz bandwidth at 2.3 GHz with
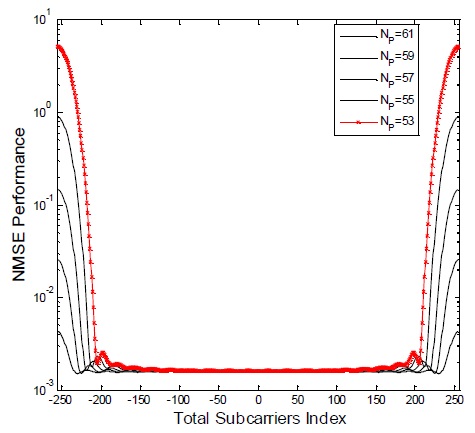
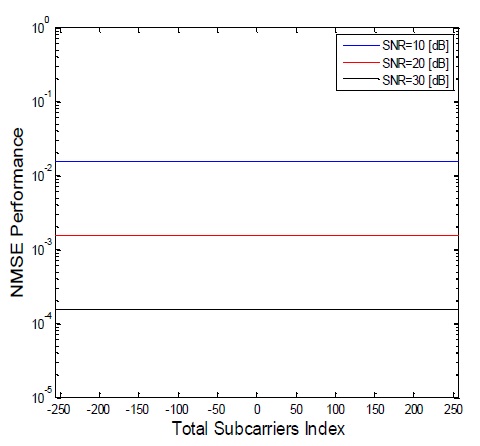
Fig. 5 shows the NMSE performance of DFT-based channel estimation in the case of no virtual carriers. It has constant values determined by the noise variance or the signal-to-noise power ratio (SNR). In contrast, Fig. 6 shows the NMSE performance in the case of virtual carriers (namely, conventional DFT-based channel estimators), which is theoretically plotted according to the total subcarriers index by using (14). The first term in (14) strongly depends on the noise variance, whereas the second term leads to the leakage. In addition, the second term is the dominant factor in performance degradation, particularly at edge subcarriers.
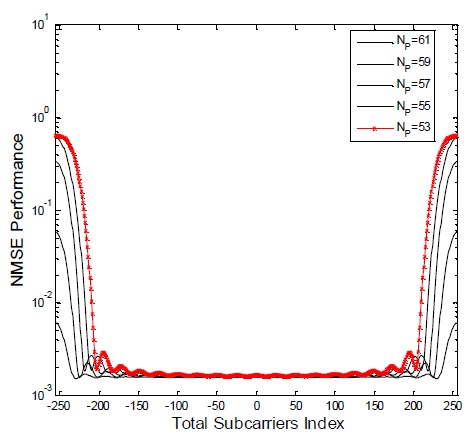
Fig. 7 shows the performance improvement resulting from the suboptimal linear estimator by using
Fig. 8 illustrates the NMSE performance of the suboptimal linear estimator with
These results denote the cases in which the
In this study, the effect of the coherence bandwidth of wireless channels on leakage suppression methods such as the optimal and suboptimal linear estimators for OFDM channel estimation was analyzed. The NMSE performances of these methods were very sensitive to the coherence bandwidth of wireless channels. If some of the estimated CFRs were placed out of the range of the coherence bandwidth, a severe channel estimation error occurred at edge subcarriers and the entire NMSE performance decreased. Further, the SNR mismatch of the suboptimal linear estimators was more critical in these cases.
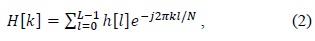
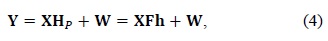
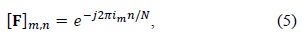
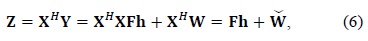
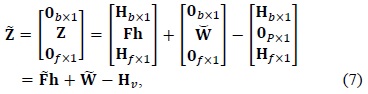
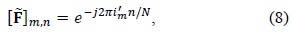
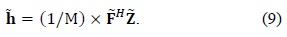
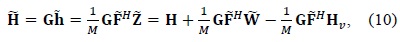
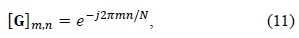
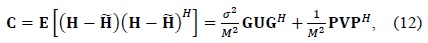
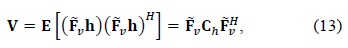
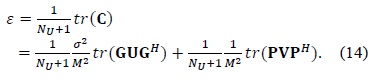
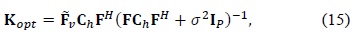
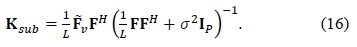
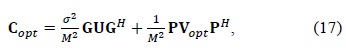
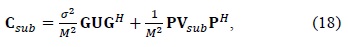
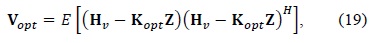
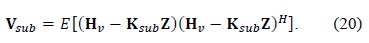
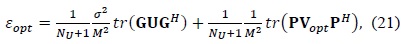
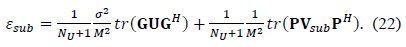

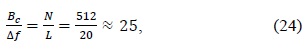
![Normalized mean square error (NMSE) performance of the conventional method (signal-to-noise ratio [SNR] = 20 dB).](http://oak.go.kr/repository/journal/16906/E1ICAW_2014_v12n4_221_f006.jpg)
![Normalized mean square error (NMSE) performance of the suboptimal method (signal-to-noise ratio [SNR] = 20 dB).](http://oak.go.kr/repository/journal/16906/E1ICAW_2014_v12n4_221_f007.jpg)