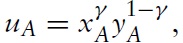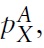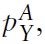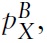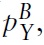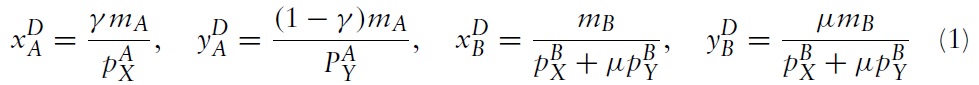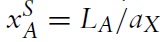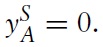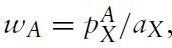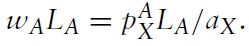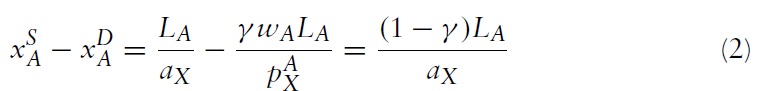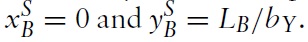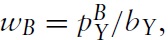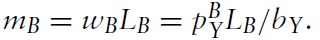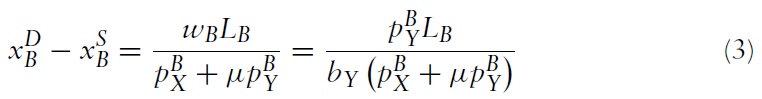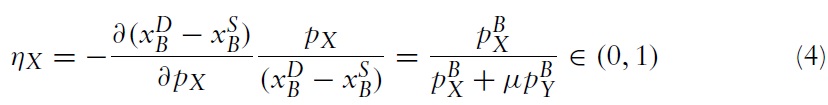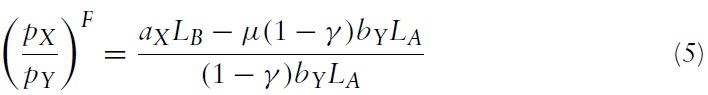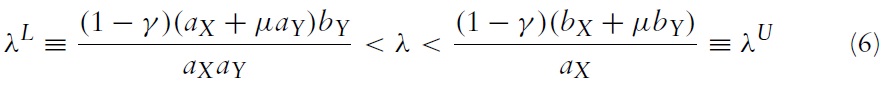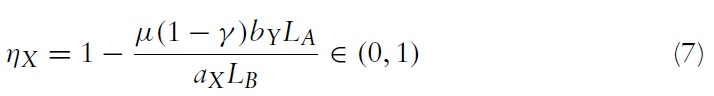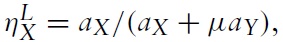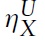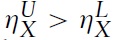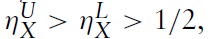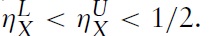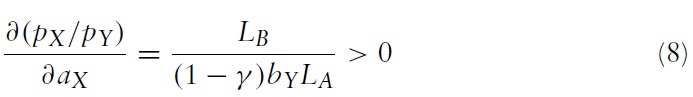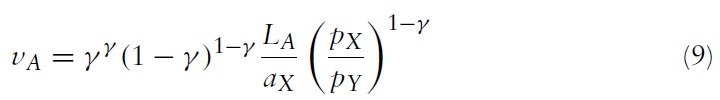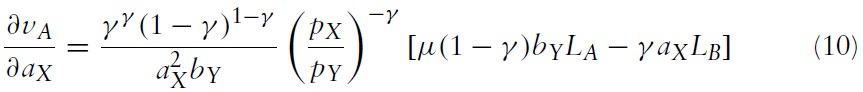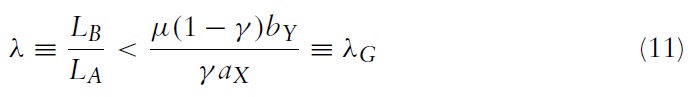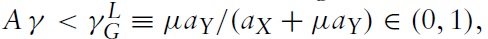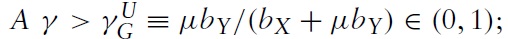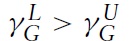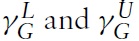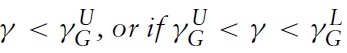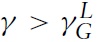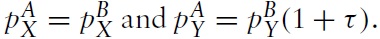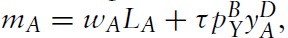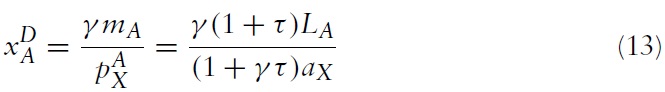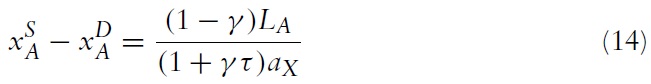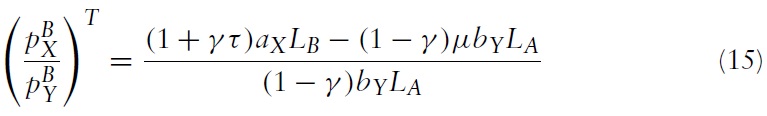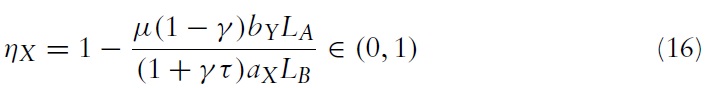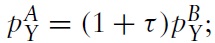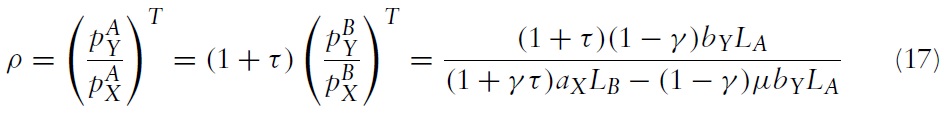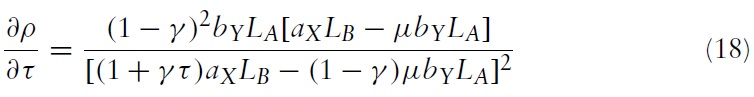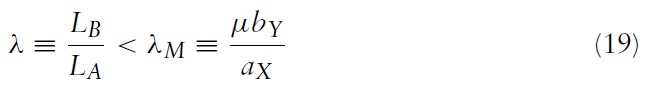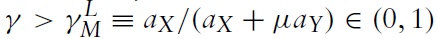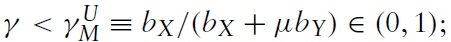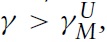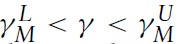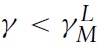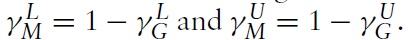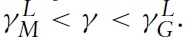Although it is 60 years since the publication of Metzler (1949a, b), the Metzler paradox still seems to be a counterintuitive result to scholars of international trade.1 The possibility that the domestic relative price of the importable good may fall when a country imposes an import tariff arises if the offer curve of the foreign country is sufficiently inelastic so that the foreign import demand elasticity is lower than the marginal propensity to consume the exportable good. Then, the improvement in the terms of trade is so large that the domestic relative price of the importable good will fall as a result of the import tariff. This paradoxical result was even doubted by Södersten and Vind (1968, 1969), but confirmed by Jones (1969). Recently, Endoh and Hamada (2005) have derived conditions that preclude the occurrence of the Metzler paradox and that require similarity of the Slutsky matrix for both countries. For import quotas, Falvey (1975) showed that the Metzler paradox will not occur, since if the Metzler paradox occurs then imports increase with a tariff and this cannot occur with an import quota, but the Metzler paradox can occur with export quotas. Results similar to the Metzler paradox have been obtained in models of international trade under imperfect competition, such as Ishikawa and Mukunoki (2008).
Another paradoxical result that may arisewhen the foreign offer curve is inelastic is immiserizing growth, and the conditions for the occurrence of immiserizing growth were derived by Bhagwati (1958). Immiserizing growth occurs when technological change (or an increase in factor endowments) shifts the production possibility frontier of a country outwards, but the primary benefit from economic growth is outweighed by the secondary loss due to the worsening of the terms of trade. Recently, Opp et al. (2009) have shown that factor growth is always immiserizing in the Heckscher-Ohlin model when the ‘Reverse Rybczynski’ effect occurs. Although many economists regard immiserizing growth as a theoretical curiosity, an empirical evaluation by Sawada (2009) claimed to have found 26 episodes of immiserizing growth. According to Jones (1985), both immiserizing growth and the Metzler paradox are best understood by looking at income effects, and both paradoxes are most likely when the income effects dominate the substitution effects.
This paper will analyse the conditions for the occurrence of immiserizing growth and the Metzler paradox in the Ricardian model using specific functional forms. A necessary condition for both paradoxes in the Ricardian model is that the foreign offer curve is inelastic, and this can be achieved by assuming that the products are perfect complements in the foreign country, whereas preferences in the home country can be represented by a Cobb-Douglas utility function. By using specific functional forms, the conditions for the occurrence of the two paradoxes will be defined in terms of the exogenous parameters of the model (demand, technology and factor endowment parameters) rather than in terms of endogenous variables such as the foreign import demand elasticity that arises in the conditions derived by Bhagwati (1958) and Metzler (1949a, b). Finally, it will also be shown that both paradoxes will occur simultaneously for some parameter values.
1The idea is actually more than seventy years old since, as Metzler (1949a, p. 17) noted, the possibility that the domestic relative price of the importable good might fall had already been discussed by Lerner (1936, pp. 310–311).
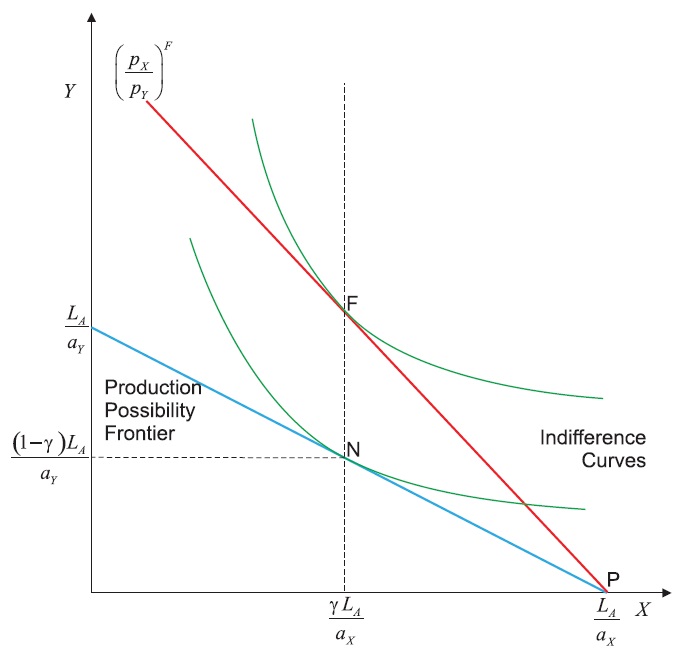
The familiar Ricardian model of international trade has two countries, the home country labelled A and the foreign country labelled B, with a labour endowment of LA in country A and LB in country B. Labour can be used to produce two goods, X and Y, using constant-returns to scale technology. The unit labour input requirements for the two goods are aX and aY in country A and bX and bY in country B, where the reciprocals of the unit labour input requirements are the marginal physical products of labour. The production possibility frontier of country A is linear and given by yA = LA/aY − (aX/aY)xA, where aX/aY is the opportunity cost of good X. Similarly, the production possibility frontier of country B is linear and given by: yB = LB/bY − (bX/bY)xB, where bX/bY is the opportunity cost of good X. Without any loss of generality, assume aX/aY < bX/bY so that country A has a comparative advantage in the production of good X.
In country A, it will be assumed that the preferences of the representative consumer are given by a Cobb-Douglas utility function:
where γ ∈ (0, 1) is the expenditure share of good X. In country B, so that its offer curve is inelastic, it will be assumed that the preferences of the representative consumer are given by a Leontief utility function: uB = Min{μxB, yB}, where μ > 0, so the products are perfect complements in country B.2 Obviously, both utility functions are homogeneous of degree one, which means that preferences are homothetic, so both goods are normal in both countries. Hence, the occurrence of the two paradoxes will not be dependent upon any of the goods being inferior goods or even Giffen goods. In country A, the price of good X is
the price of good Y is
and the wage is wA. In country B, the price of good X is
the price of good Y is
and the wage is wB. The income of the representative consumer is mA in country A and mB in country B. Given the utility functions, it is straightforward to show that the demands for the two goods in the two countries are:
Consider the free trade equilibrium, assuming complete specialisation so that the free trade relative price of good X is between the opportunity costs (autarky relative prices) of the two countries: aX/aY < pX/pY < bX/bY. Then, country A will completely specialise in the production of good X supplying
and
Its wage will be given by the marginal productivity of labour in its X industry:
so the income of the representative consumer is: mA =
Hence, the supply of exports of good X from country A is:
The free trade equilibrium in country A is shown in Figure 1 where production is at P and consumption is at F (the autarky equilibrium production and consumption is at N).
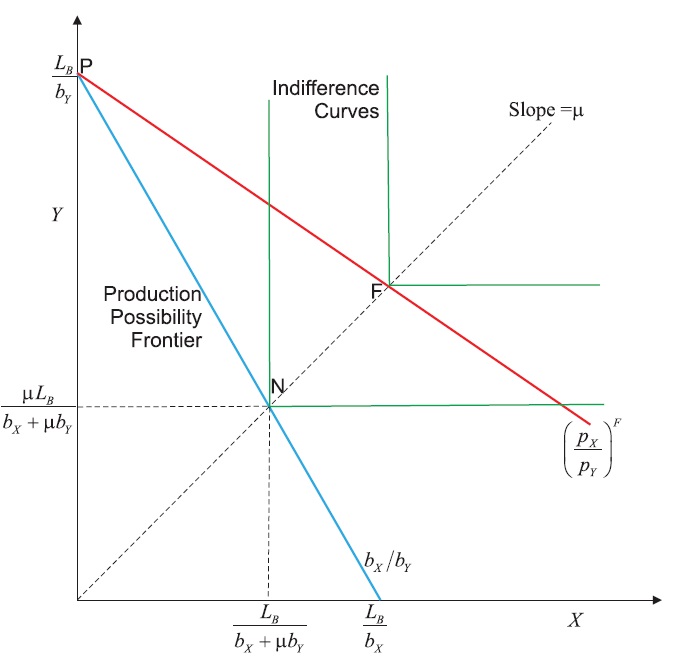
Under free trade, country B will completely specialise in the production of good Y supplying
Its wage will be given by the marginal productivity of labour in its Y industry:
so the income of the representative consumer is:
The demand for imports of good X by country B (or the demand for the exports of good X from country A) is:
The free trade equilibrium in country B is shown in Figure 2 where production is at P and consumption is at F (the autarky equilibrium production and consumption is at N).
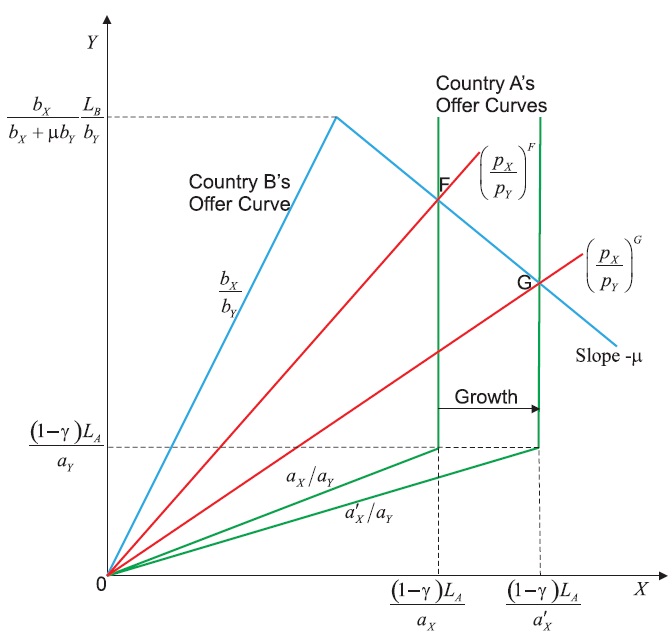
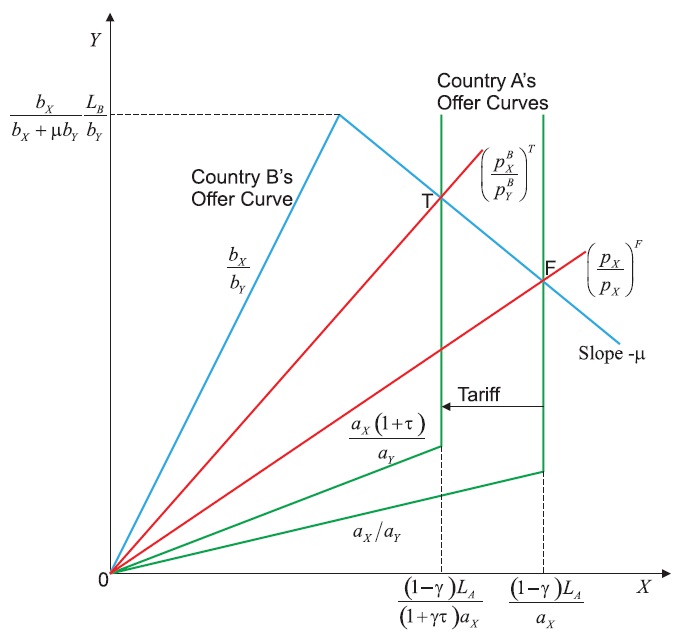
The offer curves of the two countries are shown in Figure 3, and the import demand elasticity of country B (or the elasticity of demand for exports facing country A) can be derived from equation (3):
Hence, since the import demand elasticity of country B is less than one, the offer curve of country B is inelastic so a worsening of its terms of trade will reduce its demand for imports, but increase its supply of exports. This is because the products are perfect complements in country B so the effect of the terms of trade on consumption is entirely due to the income effect as there is no substitution effect. From equation (2), the elasticity of supply of exports in country A is εX = 0 so the offer curve of country A is vertical in Figure 3, which is a feature of the Cobb-Douglas utility function, where a fraction γ of income is spent on good X, in the Ricardian model.
Under free trade, with no barriers to trade, relative prices will be the same in both countries so
Equating equations (2) and (3) yields the free trade equilibrium relative price:
The free trade equilibrium is given by the intersection of the two offer curves in Figure 3 at F where the terms of trade are pX/pY)F. The assumption of complete specialisation will be valid if aX/aY < pX/pY < bX/bY, and this will be the case if the relative labour endowments of the two countries, λ ≡ LB/LA, are between a lower and an upper bound:
It will be assumed that the labour endowments are such that this inequality is satisfied. Having derived the equilibrium terms of trade, the import demand elasticity of country B can nowbe expressed as a function of the exogenous parameters of the model by substituting equation (5) into equation (4), which yields:
The import demand elasticity of country B is an endogenous variable that is a function of the demand parameters, the technology parameters and the labour endowments. When the relative labour endowment is λ = λL, the import demand elasticity of country B is
and when λ = λU,
= bX/(bX + μbY), where it can be shown that
since aX/aY < bX/bY. The import demand elasticity of country B is decreasing in the demand parameter μ, and it can be shown that when μ < aX/aY then the import demand elasticity is always greater than one-half since
whereas when μ > bX/bY then the import demand elasticity is always less than one-half since
2The use of the Leontief utility function is a restrictive assumption, but Opp et al. (2009) also use the Leontief utility assumption. Since the products are perfect complements, there will be no substitution effect in response to a price change but only an income effect. Hence, the Leontief utility function provides a tractable way to demonstrate paradoxes that occur when the income effect dominates the substitution effect.
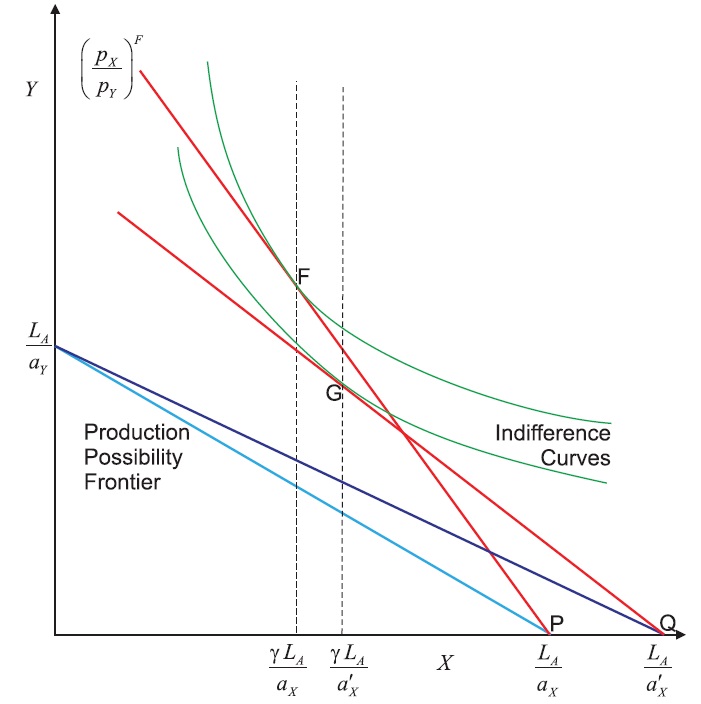
Now consider the effects of economic growth in country A in the form of technological change in the X industry that reduces the unit labour input requirement, aX. This will expand the X industry in country A and lead to a worsening of the terms of trade and the possibility of immiserizing growth first identified by Bhagwati (1958). Differentiating equation (5) yields the effect on the terms of trade:
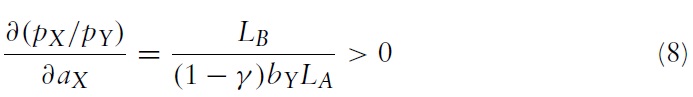
Therefore, a reduction in the unit labour input requirement will worsen the terms of trade for country A. This is shownin Figure 3 where the offer curve of country A shifts outwards as a result of the reduction in the unit labour input requirement from aX to a’X, and the equilibrium shifts from F to G with the terms of trade falling from (pX/pY)F to (pX/pY)G. The possibility of immiserizing growth is shown in Figure 4. There is an outward shift of the production possibility frontier that is biased towards the production of good X as a result of the reduction in the unit labour input requirement from aX to a’X. This shifts production from P to Q. This increase in production is more than offset by the worsening of the terms of trade, and hence the consumption of the representative consumer shifts from F to G, which is on a lower indifference curve.3
Given the Cobb-Douglas utility function, the welfare of the representative consumer in country A is given by the indirect utility function: vA = mA(pX/γ)−γ (pY/1 − γ)γ−1. Substituting the income and wage into the indirect utility function yields the welfare of the representative consumer under free trade:
To see the effect of technological change on welfare, differentiate equation (9) and use equation (8), which yields:
A reduction in the unit labour input requirement will lead to immiserizing growth if this is positive, and this will be the case if the term in square brackets is positive since all the other terms are unambiguously positive. Hence, there will be immiserizing growth if the relative labour endowment is less than the critical value:
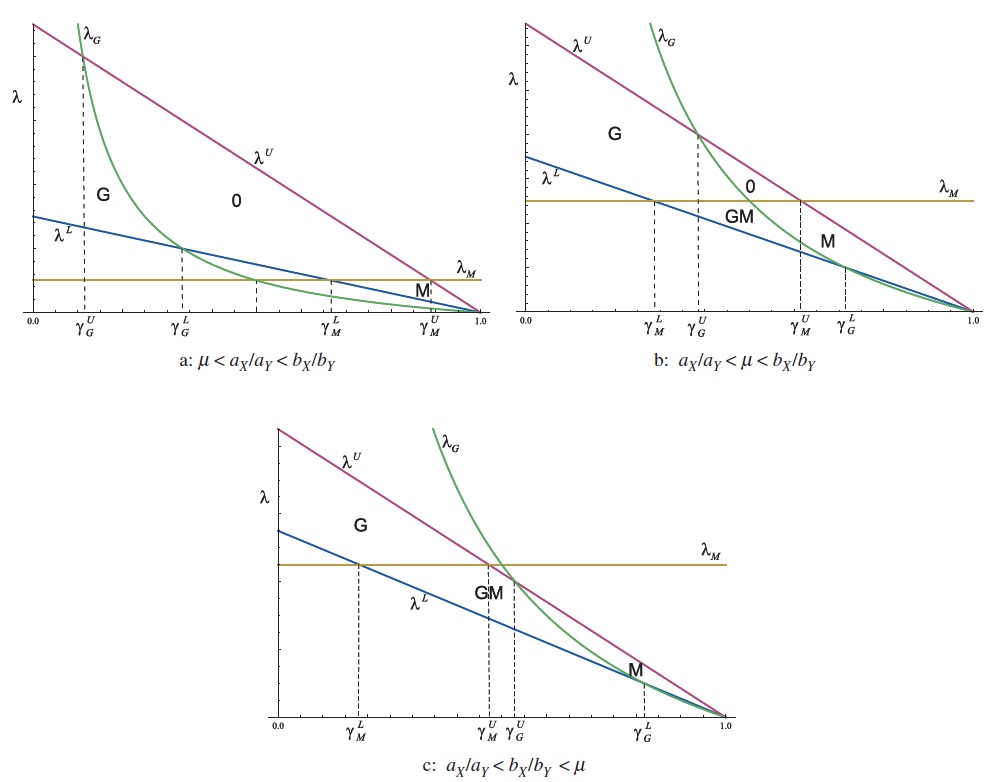
Therefore, immiserizing growth will occur if country B is sufficiently small relative to country A. The critical value is plotted in Figure 5 as a function of the expenditure share of good X in country A, γ, for three possible values of the demand parameter μ: a low value such that μ < aX/aY in Figure 5(a); a medium value such that aX/aY < μ < bX/bY in Figure 5(b); and a high value such that μ > bX/bY in Figure 5(c). There will be complete specialisation if the relative labour endowment is between the lower and upper bounds, λL and λU. It can be seen that λG > λL if the expenditure share of good X in country
and that λG < λU if the expenditure share of good X in country
where
since aX/aY < bX/bY. Immiserizing growth will occur in the regions labelled G in Figure 5. The likelihood of immiserizing growth is greatest, the lower is the expenditure share of good X in country A, γ , and the higher is the demand parameter in country B, μ, since
are both increasing in μ. This leads to the following proposition.
Proposition 1 There will be immiserizing growth if
and λ < λG, but if
then there is no possibility of immiserizing growth.
Proposition 1 provides conditions for the occurrence of immiserizing growth in terms of the exogenous parameters of the Ricardian model (the relative labour endowments, λ; the technology parameters, bY/aX; and the demand parameters, γ and μ) rather than in terms of endogenous variables, such as the foreign import demand elasticity, in the well-known condition derived by Bhagwati (1958).4 The inquisitive reader might wonder about the relationship between these results. In the case of the Ricardian model, consumption of the importable good Y is equal to imports, there is no domestic production of the importable good Y, and, with Cobb-Douglas preferences, the compensated elasticity of demand for the importable good Y is γ. Then, the condition for immiserizing growth in equation (8) of Bhagwati (1958) reduces to: ηX < 1 − γ. Using equation (7), it can be shown that this yields equation (11) so the results are consistent as one would expect.
3Immiserizing growth only occurs because the country is not pursuing its optimal trade policy, which in the case of a large country would be the use of the optimum tariff to improve its terms of trade. 4The criterion for immiserizing growth is given by equation (7) of Bhagwati (1958), which in the notation of this paper can be written as: where ε is the compensated own-price elasticity of demand for the importable good and σ is the elasticity of supply of the importable good.
Now consider the effect of country A imposing an ad valorem import tariff τ on imports of good Y. The tariff would be expected to improve the terms of trade and increase the domestic relative price of the importable good. However, Metzler (1949a, b) showed that when the foreign offer curve was inelastic then the improvement in the terms of trade may be so large that there is a decrease in the domestic relative price of the importable good. With an import tariff on good Y, the prices in country A will be
As a result of the import tariff, the income of the representative consumer in the country A is:
which depends upon the quantity of imports. Therefore, before determining the equilibrium terms of trade, it is necessary to obtain the quantity of imports as a function of the terms of trade. Substituting the prices and income into equation (1) and solving for the demand for imports of good Y in country A:
Substituting the prices and income into equation (1) and using equation (12), yields the demand for good X in country A:
The import tariff increases demand for good X in country A and, since production will not change as a result of the tariff, there will be a reduction in the supply of exports from country A. Therefore, with the import tariff, the supply of exports of good X from country A is:
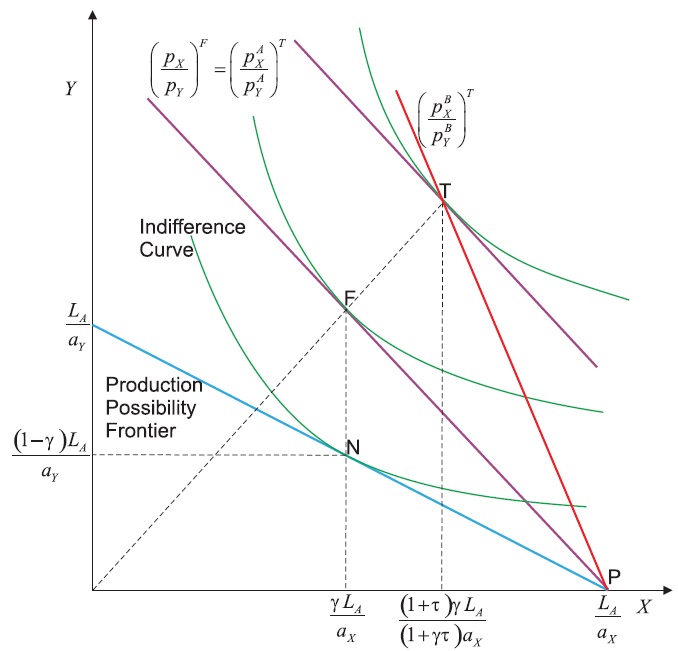
The reduction in the supply of exports is shown in Figure 6 where there is an inward shift of the offer curve of country A that shifts the equilibrium from F to T, which improves the terms of trade of country A. The equilibrium terms of trade with the tariff can be obtained by equating the supply of exports (equation (14)) with the demand for exports (equation (3)), which yields:
As expected, an import tariff will clearly improve the terms of trade of country A. Note that the import tariff will affect the import demand elasticity of country B, since substituting equation (15) into equation (4) yields:
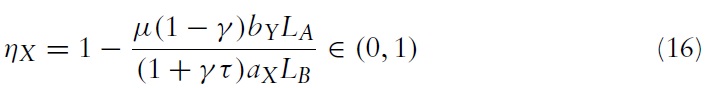
If the improvement in the terms of trade as a result of the import tariff is sufficiently large, then there may be a fall in the domestic relative price of the importable good Y in country A. Figure 7 shows the equilibrium in country A with an import tariff for the case where the improvement in the terms of trade is such that the domestic relative price of the importable good Y does not change as a result of the tariff. As shown in equation (14), the import tariff reduces exports so consumption with the tariff T must be on the dashed vertical line where exports are (1 + τ)γLA/(1 + γτ)aX. Since preferences are homothetic and the domestic prices are unchanged, consumption with the tariff T must be on the dashed ray from the origin that passes through F, which represents consumption under free trade. If the improvement in the terms of trade is greater than that shown in Figure 7 then the domestic price of the importable good Y will fall as a result of the tariff and the Metzler paradox will occur. Clearly, the tariff has increased consumption of both goods so the utility of the representative consumer has increased.
The domestic price of the importable good Y is:
hence, using equation (15), the relative domestic price of the importable good Y in country A is:
Differentiating equation (17) yields the effect of an import tariff on the relative domestic price of the importable good in country A:
Clearly, the Metzler paradox will occur if the domestic price of the importable good falls as a result of the tariff and this will be the case if the term in square brackets in the numerator is negative. Thus, the Metzler paradox will occur if the relative labour endowment is less than the critical value:
Hence, the Metzler paradox will occur if country B is sufficiently small relative to country A. The critical value is plotted in Figure 5 as a function of the expenditure share of good X in country A, γ, for three possible values of the demand parameter in country B, μ, where it can be seen that the critical value, λM, is independent of γ. It can be seen that λM > λL if the expenditure share of good X
and that λM < λU if the expenditure share of good X
where
since aX/aY < bX/bY. The Metzler paradox will occur in the regions labelled M in Figure 5. The likelihood of the Metzler paradox is greatest, the higher is the expenditure share of good X in country A, γ, and the higher is the demand parameter in country B, μ, since
are both decreasing in μ. This leads to the following proposition.
Proposition 2 There will be a decrease in the domestic relative price of the importable good as a result of an import tariff (the Metzler paradox) if
or if
and λ < λM, but if
then there is no possibility of the Metzler paradox.
Proposition 2 provides conditions for the occurrence of the Metzler paradox in terms of the exogenous parameters of the Ricardian model rather than in terms of endogenous variables, such as the foreign import demand elasticity, in the well-known condition derived by Metzler (1949a). Assuming the initial tariff rate is zero, Metzler (1949a) showed that the domestic relative price of the importable good will fall if the foreign import demand elasticity is less than the marginal propensity to consume the exportable good. With the Cobb-Douglas utility function in country A, the marginal propensity to consume the exportable good X is γ, so the condition from Metzler (1949a) reduces to ηX < γ. Using equation (7), it can be shown that this yields equation (19) so again the results are consistent even though equation (19) does not depend upon the demand parameter γ. Equation (12) of Metzler (1949b) provides a general condition for the Metzler paradox when the tariff is non-zero and the tariff revenue is redistributed to the consumer in a lump-sum manner,which again can be shownto be consistent with Proposition 2.
Finally, having derived the conditions for immiserizing growth and the Metzler paradox, it is interesting to compare these two conditions and to consider the possibility of the simultaneous occurrence of both paradoxes in a country. Comparing the critical values of the expenditure share of good X in country A, γ, for the Metzler paradox with the analogous values for immiserizing growth, it can be shown that
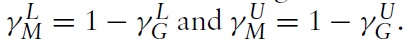
In addition, recall that the condition for immiserizing growth in terms of the foreign import demand elasticitywas that ηX < 1 − γ whereas the condition for the Metzler paradoxwas that ηX < γ. Therefore, and as shown in Figure 5, immiserizing growth is most likely to occur for low values of γ whereas the Metzler paradox is most likely to occur for high values of γ, and when γ = 1/2, the two critical values are equal, λG = λM. The occurrence of both paradoxes is possible for some parameter values as can be seen from Figure 5 depending upon the value of the demand parameter in country B, μ. For low values, when μ < aX/aY as shown in Figure 5(a), where the foreign import demand elasticity is always greater than a half, ηX > 1/2, the two paradoxes do not occur for the same parameter values, and there is a region, labelled 0, where there are no paradoxes. For medium values, when aX/aY < μ < bX/bY shown in Figure 5(b), the paradoxes both occur in the region labelled GM, and there are no paradoxes in the region labelled 0. For high values, when μ > bX/bY shown in Figure 5(c), where the foreign import demand elasticity is always less than a half, ηX < 1/2, the paradoxes both occur in the region labelled GM, and, in this case, one or both of the paradoxes always occurs. These results lead to the following proposition.
Proposition 3 If μ > aX/aY then both immiserizing growth and the Metzler paradox occur for the same parameter values when λ < λG and λ < λM, which will only be the case for
The occurrence of both paradoxes will occur if the foreign import demand elasticity is sufficiently low and, since the import demand elasticity of demand is decreasing in the demand parameter in country B, μ, both paradoxes will occur when μ is sufficiently large.
The conditions for the occurrence of immiserizing growth and the Metzler paradox have been derived in the Ricardian model. Rather than derive general conditions, as in Bhagwati (1958) and Metzler (1949a,b), which are expressed in terms of endogenous variables such as the foreign import demand elasticity, specific functional forms have been used to derive conditions in terms of the exogenous parameters of the model. In the Ricardian model, a necessary condition for both paradoxes is that the foreign offer curve is inelastic. Therefore, it was assumed that the products were perfect complements in country B, which yields an inelastic offer curve since there are only income effects from changes in the terms of trade and no substitution effects.5 Although an inelastic foreign offer curve is a necessary condition for both paradoxes, it is not a sufficient condition for either of the paradoxes. Conditions for both paradoxes were derived in terms of the demand parameters, the technology parameters and the labour endowments. By using specific functional forms it was possible to characterise the occurrence of both paradoxes for the entire parameter space. Immiserizing growth was shown to occur when the expenditure share of the exportable good was sufficiently low, whereas the Metzler paradox was shown to occur when the expenditure share of the exportable good was sufficiently high. Finally, it was shown that both paradoxes may occur for some parameter values, particularly when the foreign import demand elasticity was sufficiently low, which would be the case when the demand parameter μ was sufficiently large.
5The importance of income effects for the explanation of many paradoxes in international trade has been stressed by Jones (1985).