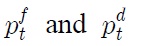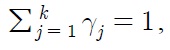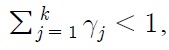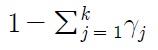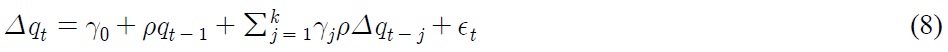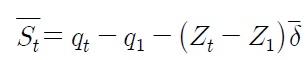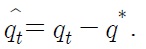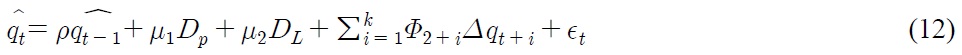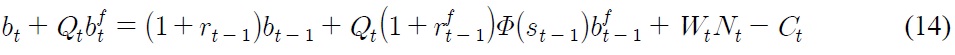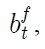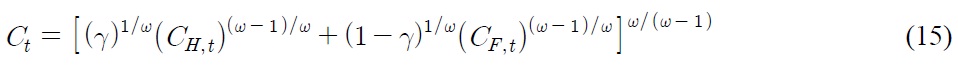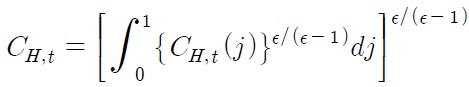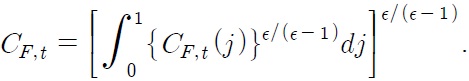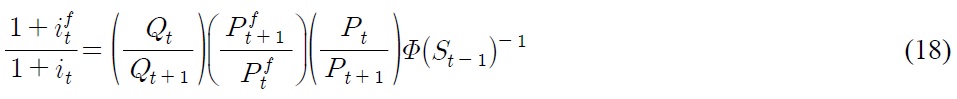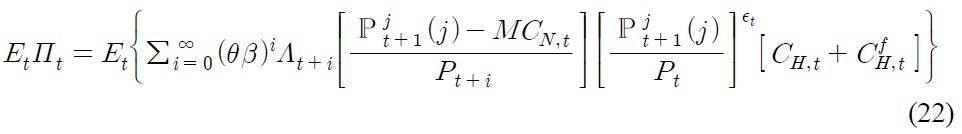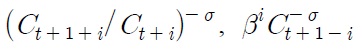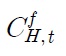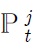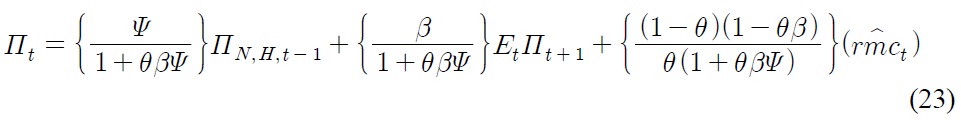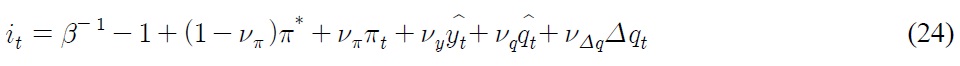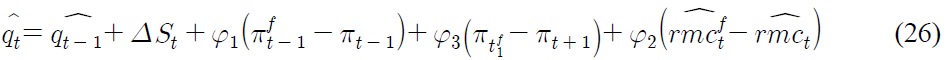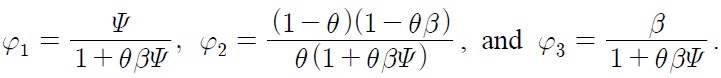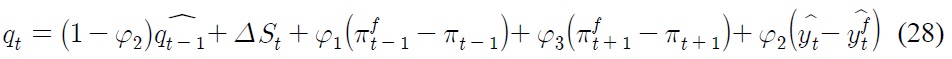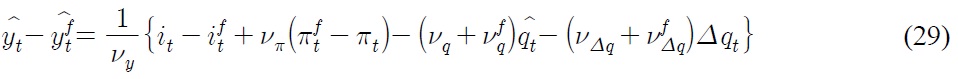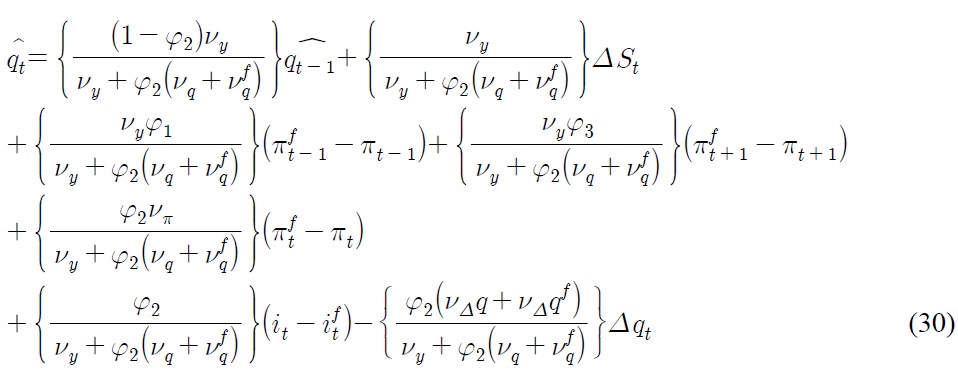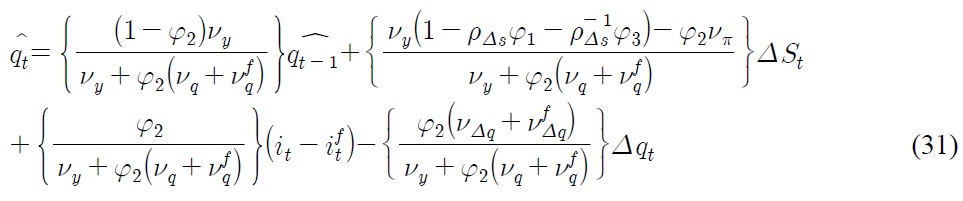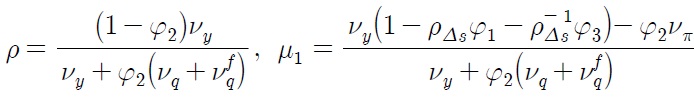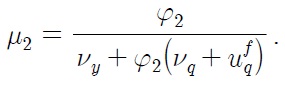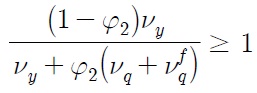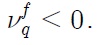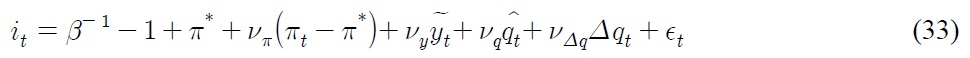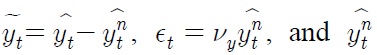Purchasing power parity (PPP) as an exchange-rate determination model seems to strike back recently after going through the dark ages of voluminous disastrous empirical testing on its validity
The allowance for structural breaks in testing for PPP is not entirely new. Of late, the empirical testing of the unit-root null with structural breaks in searching for strong evidence of PPP has shed its lights on the East and Southeast Asian currencies, which evidently fulfill the treatment of structural breaks, especially in the aftermath of the currency crash in 1997/98. For instance, Wu
Although there is mounting evidence of stationary real exchange rates, the evidences remain indecisive due to the potential pitfall of arbitrary predetermining the threshold value and time period of a structural break out of the data-generating-process, as in the tradition of Perron (1998). In previous studies, Zivot and Andrew (1992) caution that a simple inspection of the breakpoint based on data observation can be misleading as sudden changes in data can be mistakenly interpreted as realization from the tail of distribution of the underlying data generating process. One should call this exogeneity into question for a very basic concern: how likely it is to overlook other breaks not observably as apparent as a nose-diving currency crash, yet significant in reverting the real exchange rates to the parity?
Subsequently, Zivot and Andrew (1992), Perron (1997), Vogelsang and Perron (1998), to name a few among many others, propose a unit root testing procedure with break points that are not known
Consistent with this line of thought, the objective of this paper is to revisit the test of the unit-root null in the presence of structural breaks in two directions. First, at the empirical front, this paper attempts to expand the literature by allowing for more than one endogenously determined structural break in unit root testing. Ben-David
Second, at the theoretical front, the idea of a structural break captured by means of econometrics without justifying the structural properties seems to be theoretically ill-defined. This paper contributes to the literature by laying out an open-economy New Keynesian model to more systematically characterize the sources of structural breaks and mechanism of a unit root in the real exchange rate. Most interestingly, the model attributes nonstationarity in real exchange rates to the optimally conducted monetary policy for inflation targeters like Korea in conjunction with an endogenous currency risk premium.
The subsequent discussion is organized as follows. Section 2 reviews the idea of PPP, elaborates on the inappropriateness of existing testing procedures, and illustrates our modeling strategy. We discuss the main results in Section 3. It is then followed by a formalization of structural breaks in Section 4. Section 5 concludes.
1The classic Rogoff (1996), based on the numerous disappointing results of the empirical validation of PPP, reached a rather gloomy assessment that PPP theory is ‘something of an embarrassment’. A more recent Taylor and Taylor (2004), however, conclude that long-run PPP may hold in the sense that there is significant mean reversion in the real exchange rates, despite the fact that short-run PPP does not hold. To see the flow of development over the years in finding PPP, one can refer to Froot and Rogoff (1995), Sarno and Taylor (2002) , and Taylor (2006). 2See Taylor (2006) for a non-exhaustive list of recent works. It includes Holmes (2010), which allows for Markov switching between a non-stationary and stationary regime, and between stationary regimes with different degrees of persistence. Also included are Baharumshah et al. (2010) who emphasize the nonlinearity in a mean-reverting process of real exchange rates, Ho et al. (2009) who couple real exchange rate stationarity to geographical factors and variability in inflation and nominal exchange rates, and Kocenda (2005) who allows for a single endogenous break in real exchanges. 3Nonlinearity in a mean reversion process of real exchange rates has been another competitive candidate. One can see, for instance, Taylor and Taylor (2004), Taylor (2006), Baharumshah et al. (2010) for the pros of the nonlinearity approach. 4One of the most fascinating advantages of the LM test over other unit-root tests with structural breaks is that it has a test statistic that is invariant to the breakpoint nuisance parameter and thus does not require the assumption of no break(s) under the null to ensure that the test statistic is invariant to breakpoint nuisance parameters, as other tests did.
Ⅱ. Testing for Real Exchange Rate Stationarity
The purchasing power parity (PPP) hypothesizes that exchange rates between two currencies adjust to reflect domestic and foreign price levels (in logarithm):
where
correspondingly refer to the foreign and domestic price levels, and
where
where
The real exchange rate
The coefficient
where
That said, we consider the following data generating process with a
where the error term
If
the process that drives
shock to the real exchange rate vanishes in the long run at the rate of
per time period. We reparameterize Eq. (6) to produce the following empirical equation
The most commonly used test is the augmented Dickey-Fuller (ADF) test proposed by Dickey and Fuller (1981) under the unit root null hypothesis of ρ = 0. Rejection of the null suggests little tendency for deviations from PPP.
One limitation of the conventional ADF unit root test is the inability to recognize PPP when it actually holds outside the structural shift. Montanes and Clemente (1999), Aggarwal
Lee and Strazicich (2001) further argue that the ADF-type endogenous break test tends to incorrectly select the break point, and more so should the magnitude of the break increase. At this misspecified break point, the persistence is biasedly maximized, resulting in a spurious rejection of the unit root null. Accordingly, Lee and Strazicich (2003) propose a one-break LM unit root test as an alternative to Zivot-Andrews test, and a two-break LM unit root test for Lumsdaine-Papell test. Contrary to the ADF-type test, the size properties of the LM unit root test are fool proof to the presence of breaks under the unit root null. As such, the LM unit root test, which allows for structural breaks under both unit root null and stationary alternative, is able to obviate the invalid estimation of break points and spurious rejection. For this reason, this paper adopts Lee and Strazicich (2003)’s LM unit root test with two breaks.
1. LM Unit Root with Two Endogenous Structural Breaks
Consider Lee and Strazicich (2003)’s procedure that corresponds to Perron (1989)’s Model C that allows for two changes in both level
where Δ is the difference operator. The vector of exogenous variables,
is a detrended series such that
for t = 2, ...
denotes coefficients in the regression of Δ
The unit root null hypothesis
The critical values for the two-break minimum LM unit root test statistics are tabulated in Lee and Strazicich (2003).
5We do not consider Model B as it is commonly believed that most economic time series can be adequately accommodated by Model A and C. Sen (2003) suggests that Model C yields more reliable estimates as compared to Model A, and the former is thus preferred to the latter when a break point is endogenously determined (see, also, Shively, 2000 and Narayan, 2005). For this reason, we consider only Model C.
In this section, we examine the real exchange rates of six East Asian economies, namely Indonesia, Korea, Malaysia, Philippines, Singapore, and Thailand over the time period January 1993 to July 2010. Here, we treat the U.S dollar as the numeraire since the U.S has long been Asia’s major trading partner, particularly as the final destination for regional production, not to speak of its role as the dominant vehicle currency in international trade (Goldberg and Tille, 2008)
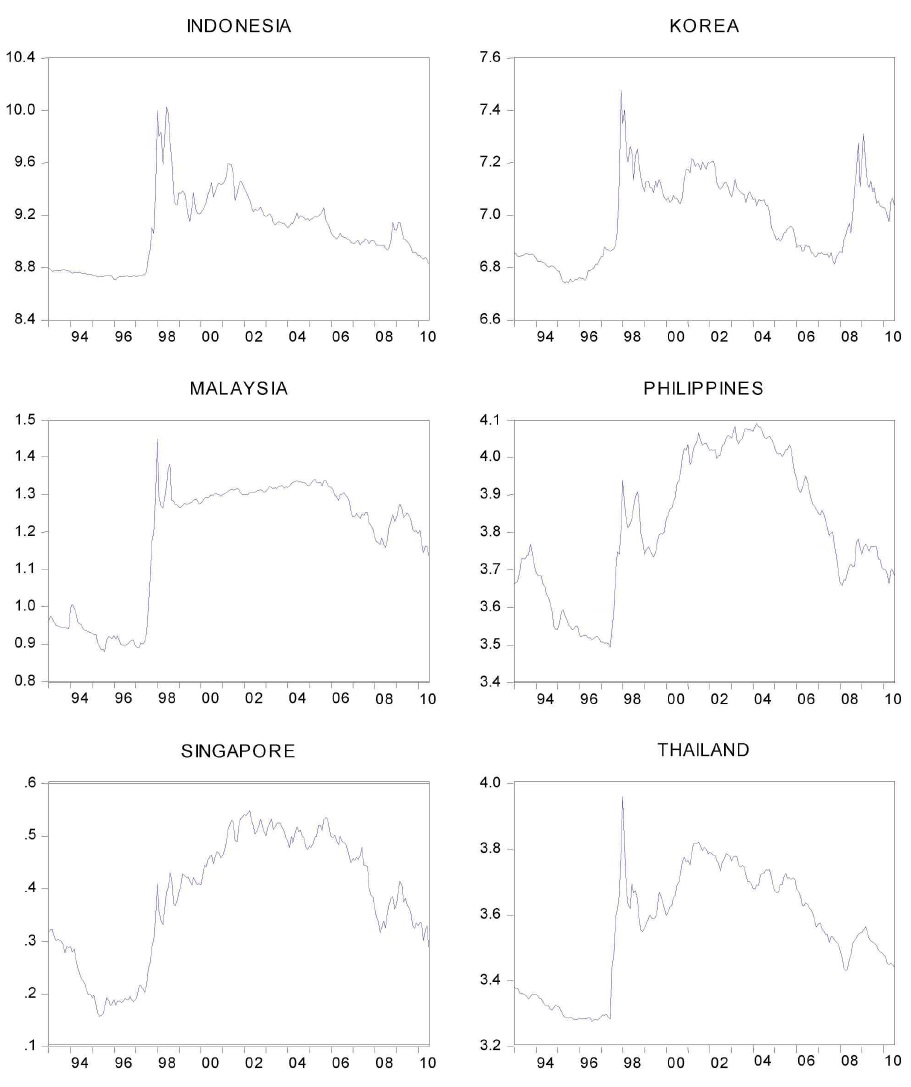
Figure 1 illustrates the variability of real exchange rates for six Asian economies throughout the years of 1993 and 2010. The sudden and drastic upsurge in real exchange rates during the Asian crisis apparently dominates the scene, suggesting a potential structural shift in the mean and trend of the data after 1997. It is thus interesting to know whether Asian real exchange rates are characterized by unit roots or is indeed trend-stationary that is just subject to structural breaks. Equally fascinating is the fact that, to find another break without hesitation through an informal eyeballing of Figure 1, is barely possible. This difficulty suggests that allowing the breaks to be endogenously determined is a sensible implementation.
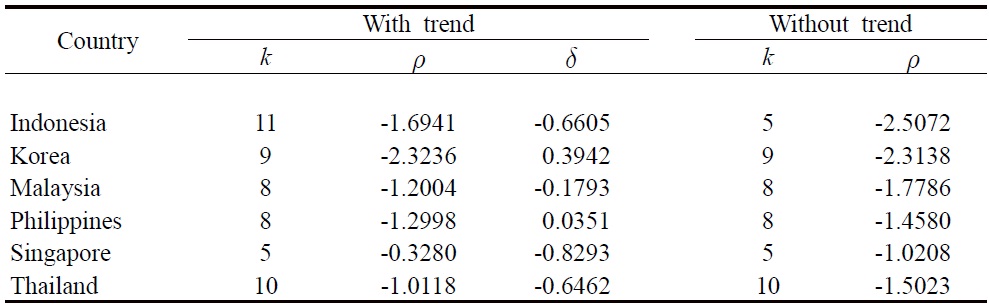
We begin the empirical analysis with the ADF test that serves as a benchmark for comparison. The test includes a deterministic trend to accommodate the potential time trends in the relative consumer prices driven by Balassa- Samuelson effect. Using the ‘general-to-specific’ recursive

ADF Test Results
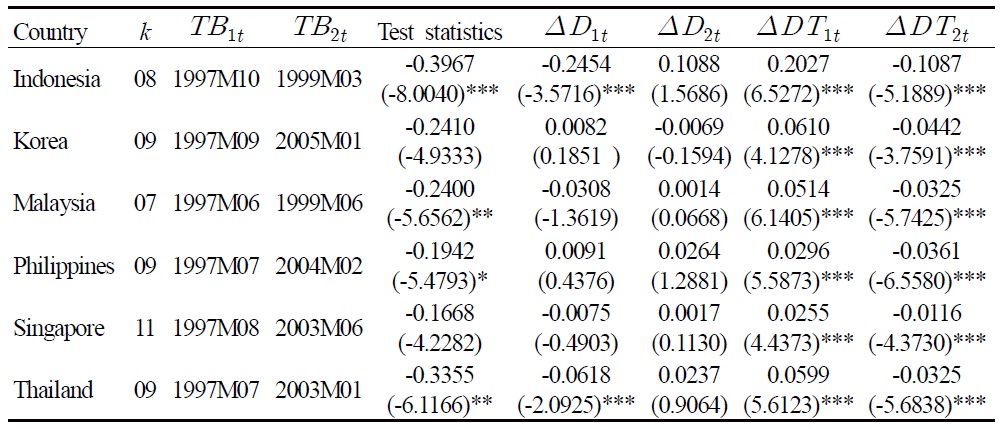
As expected, the unit root null cannot be rejected. One typical response to such findings is to fault the tests for their lack of power. But as noted previously, the failure to incorporate structural changes in testing the unit root of a time series is too often biased toward finding nonstationarity (see Rappoport and Reichlin, 1989). In view of the potential instability of the PPP relationship associated with exceptional events like the onset of Asian currency crisis, unit root tests that permit level and trend breaks are naturally sensible for analyzing the long run behavior of the real exchange rates. Indeed, by applying the LM unit root test with two endogenous breaks, we find evidence in favor of the PPP hypothesis. The results of the two-break LM unit root test are presented in Table 2.
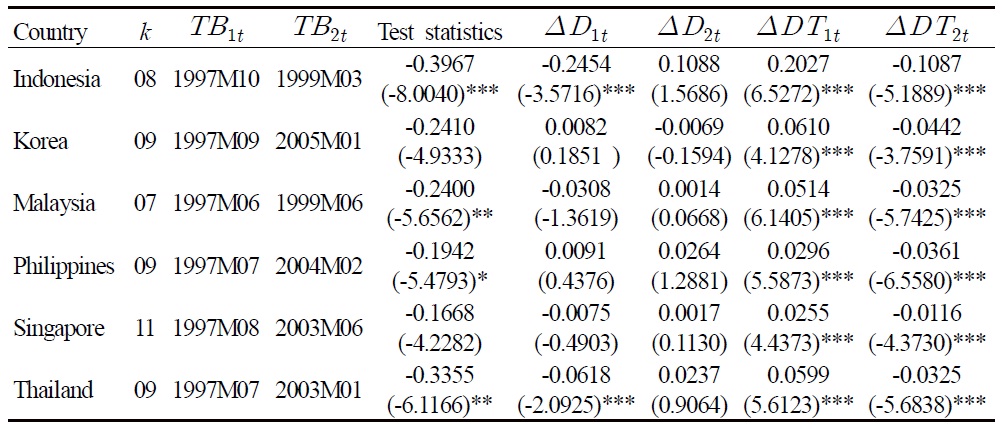
Two-break LM Tests
Table 2 reveals that the unit root null can be rejected in favor of the trend-break stationary alternative for four of the six real exchange rates (Korea and Singapore are the exceptions), out of which three are at least at a 5% significant level. As the minimum LM tests assume breaks under the null, rejection of the unit root null profoundly confirms that the real exchange rates of these Asian countries are trend-stationary and are subject to structural change. Interestingly, the results also indicate that a trend break is statistically more critical than a level-break in accounting for real exchange rate stationarity.
Because the minimum LM test endogenizes the determination of break points, the outcome is foolproof to the criticism of arbitrarily imposed break dates (Christiano, 1992). The first estimated break points collectively appear within June and October of 1997. This finding is certainly consistent with the onset of the Asian currency and financial crises since July 1997. More puzzling is the heterogeneous second estimated break points that fall unsystematically in between 2003 and 2005. Unlike the first estimated break points, these second estimated breaks are not cursorily observable in the figure, which of course substantiates the importance of endogeneity in break determination. Of further interest is whether a mechanism that is able to consistently account for this variety of break points can be found.
6Baharumshah et al. (2007) showed that mean reversion of real exchange rates in the framework of a panel unit root test without break for a set of countries exactly identical to ours appears to be invariant to the choice of the numeraire currency. Nusair (2008) also concludes that base currency is not critical to the finding of long-run PPP.
Ⅳ. An Interpretation of Structural Breaks in the New Keynesian Model
Conceptually, the path of real exchange rates (in logarithm) can be described as
where
We can augment Eq. (11) to conceptually resemble Perron (1989)’s Model C of structural break (ignoring time trend and constant):
where
Consider an economy with working households endowed with one-period state-contingent bonds. Human and non-human incomes finance non-storable consumption and purchase of assets. Household’s problem, therefore, can be written as to maximize the discounted future streams of utility,
subject to the budget constraint
where
is the real exchange rate,
On top of that,
respectively, denote real domestic and foreign bonds that pay real yields.
where
and
Derived from the first-order conditions, the marginal rate of substitution between consumption and hours worked is given by
Besides, the consumer’s optimality condition with respect to intertemporal consumption allocation can be derived as
where
and the definition of real exchange rate, we can get
Consider now a simple production function of firm
By denoting the shadow price of the Lagrangian problem as real marginal cost (
Firm
in order to maximize the expected discounted profits (
where
denotes the discounted factor in the interest of households.
is home export. Eq. (22) assumes producer currency pricing in exporting, and the pricing decision is symmetrical for all firm
In a Calvo price setting, firms that receive signals at probability 1 –
derived from Eq. (22). Those that have not received the signal at probability
To close the model, we assume the following monetary policy function:
The sum of the first two items on the right hand side amounts to the targeted nominal interest rate. The coefficients
2. Deriving the sources of unit root and structural breaks
Consider the definition of real exchange rate. The log deviation of real exchange rates can be written as
The inflation differentials in Eq. (25) can be substituted by the difference between the New Keynesian Philips curve of foreign and home economy, which simplifies to
where
Next, Pareto efficient allocation ensures that
Together with the foreign counterpart of Eq. (27) and Eq. (19), Eq. (26) can be further simplified to
The last resolution is to put monetary policy into Eq. (28). Rearrange the home monetary policy function of Eq. (24) and identical foreign monetary policy function in such a way that
Substitute Eq. (29) into Eq. (28), we get
where further simplification gives us
Eq. (31) resembles Eq. (12) in that
and
According to Eq. (30), interest rate differentials
due to asymmetry in the conduct of monetary policy, constitute the break in the level of real exchange rate, whereas nominal depreciation rate and inflation differentials contribute to the break in steepness of the trend of real exchange rate. The magnitude of each source of break depends on the degree of price stickiness, which influences the value of
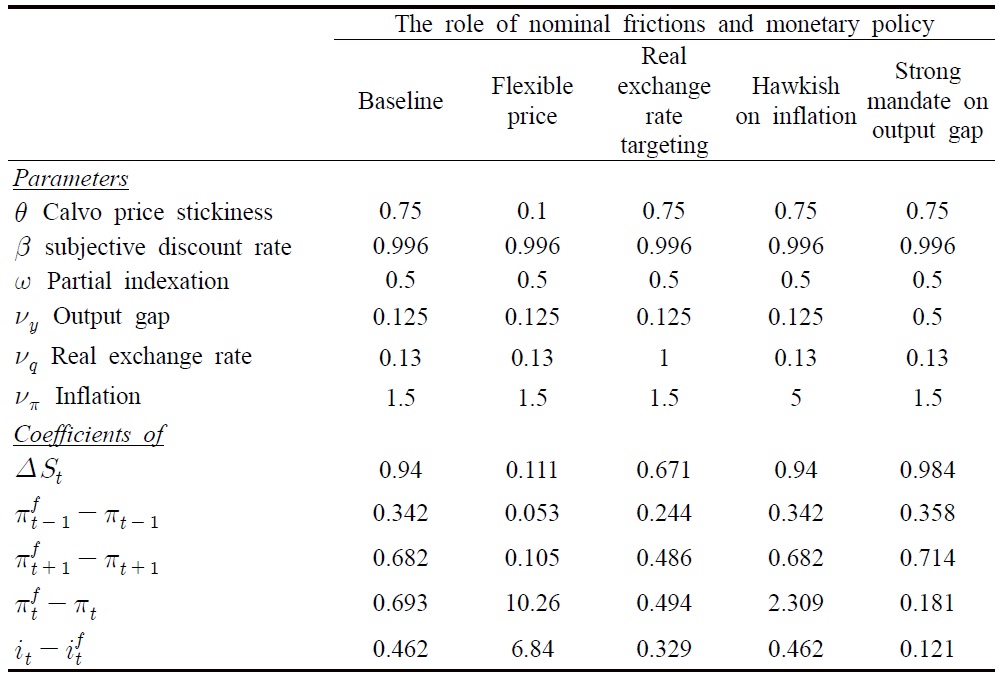
In particular, results contained in Table 3 show that:
[Table 3] Effects of Nominal Rigidities and Monetary Policy in Generating Structural Breaks
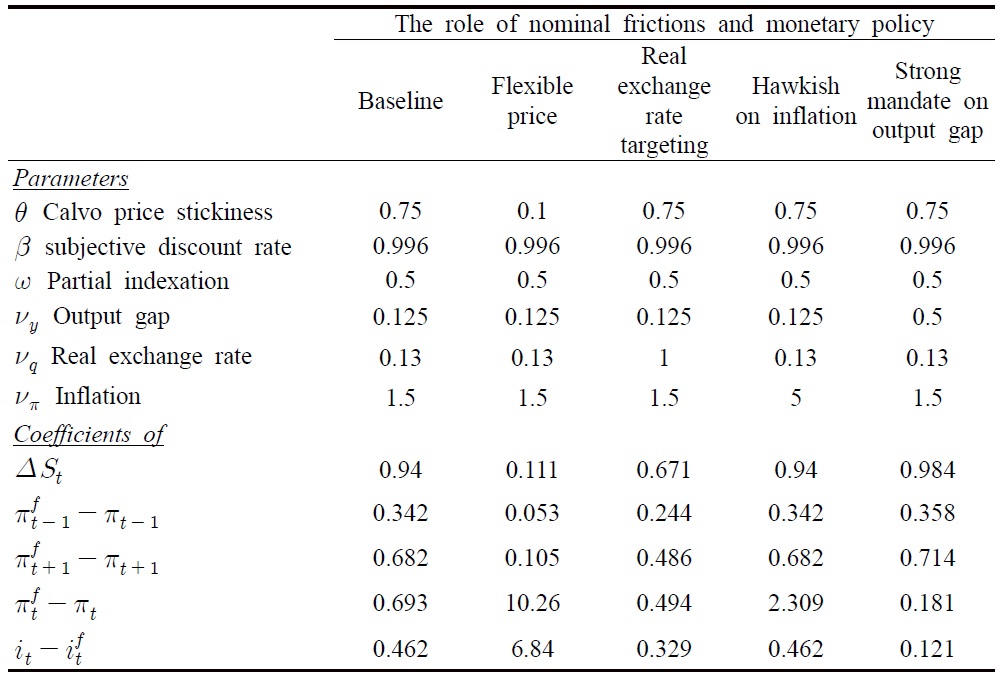
Effects of Nominal Rigidities and Monetary Policy in Generating Structural Breaks
4. Explaining nonstationary real exchange rate
Can our model explain why the unit root null hypothesis for the case of Korea, for instance, cannot be rejected even when breaks are accounted for? The answer lies in Eq. (30). As real exchange rate is described as a unit-root process if
which simplifies to
Sanchez (2009) has interestingly found that the Bank of Korea places negligible emphasis on both output and the exchange rates. This implies
And what matters the most is
The intuition is straightforward, particularly for inflation targeters like Korea. Let us rewrite Eq. (24) in terms of output gap
where
denotes the log deviation of natural output from its steady state. Suppose there is a productivity progress that increases the natural output over the steady state, and the variance of the productivity shock
On the other hand, as price tends to fall in the aftermath of a favorable productivity shock, the optimal monetary response for inflation targeters like Korea requires a contemporaneous fall in interest rate to accommodate the rise in natural output. Put in our context, a fall in nominal and thus real interest rate below a long-run average, given the sticky-price environment, causes a level-break in real exchange rates. Because real depreciation is expansionary and facilitates a central bank’s task to close the output gap in order to stabilize the inflation, inflation targeters can be tolerant of real depreciation such that
This paper reconsiders real exchange rate stationarity in the framework of the minimum Lagrangian Multiplier unit root test that can account for two endogenously determined structural breaks. Allowing for endogenous break determination and explicit consideration of breaks under the unit root null have been the two main pillars that make this procedure the most appropriate one in testing for real exchange rate stationarity. Our results are mixed. Some exhibit trend-stationary real exchange rates, while some others did not. This motivates us to address two important questions: What constitutes structural breaks? And what drives the unit root process?
By shedding lights on a simple New Keynesian model, we conjecture that an interest rate differential is the source of a level-break, whereas the rate of nominal depreciation and inflation differentials can instigate a mean-break. The magnitude of each factor is largely influenced by the degree of price stickiness and the central bank’s preference toward inflation, output and real exchange rate stabilization. We further show that the conduct of monetary policy that places negligible emphasis on real exchange rate moderation can result in nonstationary real exchange rates, particularly when the currency risk premium is increasing in the level of nominal exchange rates.
What is particularly important, but is out of the scope of this paper and thus is of interest for future study, is certainly the quantitative evaluation of the model of real exchange rate nonstationarity based on individual country experience. Because persistent deviation of real exchange rates from the long-run average can end with crisis-provoking resource misallocation, probing into the relationship between optimal monetary policy and real exchange rate nonstationarity shall be a promising venue for future study.