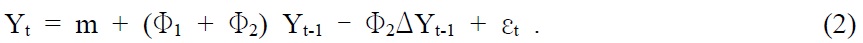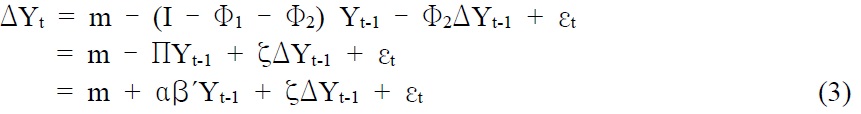This paper examines the interactions among immigrants, inbound FDI, and imports in the U.S. In testing the patterns of international movements of factors of production, most existing analyses have omitted the role of international trade. On the other hand, research on the relationship between FDI and international trade has neglected the importance of international labor movements. This study uses a vector error correction model to consider all three variables. Using U.S. annual data from 1969 to 2000, we find that labor and FDI move in the same direction and labor movements cause FDI movements. In addition, it is also found that inbound FDI and imports are substitutes.
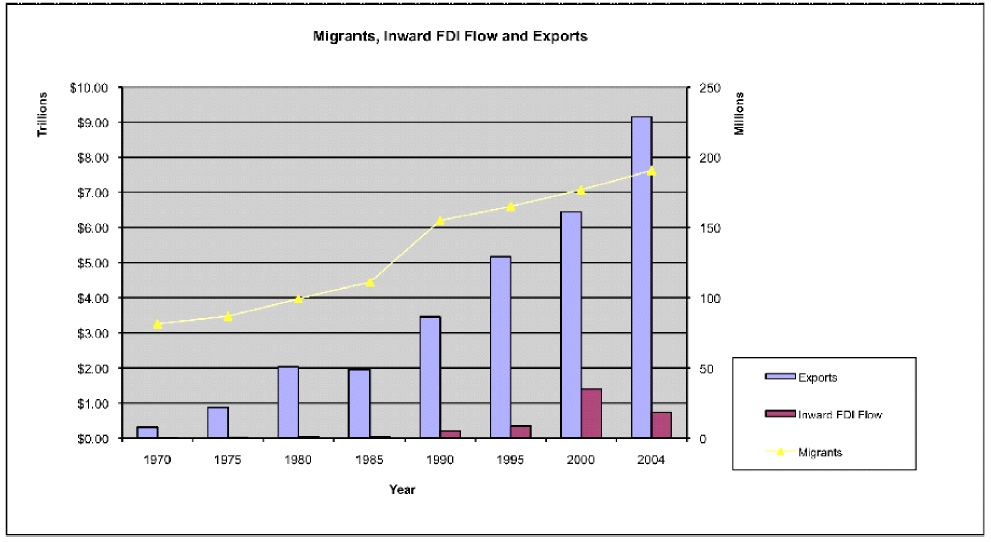
Our world is getting smaller every day with the astonishing pace of economic globalization. During the last three decades, international trade volumes have outgrown production. In the case of foreign direct investment (FDI), FDI stocks reached over $8.1 trillion and accounted for about 23 percent of the world gross domestic product (GDP) in 2003.1 International labor movements (immigration) have also grown rapidly. The UN estimates a total of between 185 million and 192 million migrants in 2005.2 According to
As a result, understanding the connections between the flow of goods, capital, and labor has been an important focus for economists and policymakers. However, previous academic research invariably examines only two of these three flows.
For example, there are an extensive number of studies examining the linkages between international trade and FDI. Theoretical models predict both the substitution and complementarity effects of FDI on international trade. In particular, theories predict that FDI substitutes for international trade when FDI is performed by horizontal multinational firms with multiple plants around world, producing identical or very similar products in each plant, while vertical FDI models, where firms use low-wage countries for assembly before shipping products back to the home country, predict complementarity. Most empirical studies, however, have shown the complementarity relationship between international trade and FDI. Even though horizontal multinational firms dominate FDI activities, there is no empirical finding supporting a substitution effect of FDI on international trade at the aggregate country level.3
Likewise, there have been many empirical and theoretical efforts inquiring into the international movements of capital and labor. The simple neoclassical trade and growth model – two countries, two factors of production, and two goods – predicts that capital and labor move where they can get the highest return. Therefore, capital should move from the capital-abundant country to the capital-poor country that has a higher marginal product of capital. Thus, in a two-factor model, capital and labor should move opposite of each other. Empirically, however, the neoclassical prediction has not been supported by the available evidence. In contrast with the neoclassical prediction, capital flows to other capital-abundant countries. In his 1990 paper, Lucas shows the possibility that poor countries’ marginal product of capital is actually not high enough to attract foreign capital inflow. Lucas suggests that rich countries are more productive than poor countries because rich countries have more human capital.
An issue with all of these two-variable studies is the possibility that ignoring the third variable leads to incorrect inferences due to endogeneity bias. For example, without considering international trade of goods and services, the empirical results on international movements of factors of production could be biased or misspecified. International factor movements clearly affect the domestic capital-labor ratio, so that domestic production of goods and services could be changed in accordance with international factor movements. Therefore, the international flow of goods and services can be affected by international movements of factors of production, and these trade changes will cause another international movement of factors of production as a consequence. Therefore, ignoring international trade variables could bring not only specification problems, but also an endogeneity problem.
The main contribution of this study is to provide the first empirical analysis of which we are aware that includes all three major international variables – immigrants, FDI, and trade – in a vector error correction model to estimate how these variables are correlated with each other. We examine a model with three variables in which immigrants, inbound FDI, and imports interact simultaneously. We also estimate models with two variables in order to compare our results with previous empirical findings. Using bilateral data on U.S. annual immigrants, inbound FDI, and imports from 1969 to 2000, we find that labor and capital move in the same direction and labor movements (immigration) bring about capital flows. In addition, we also find that inbound FDI and imports are substitutes, which is the first empirical finding supporting a substitution effect of FDI on international trade at the aggregate country level. According with the theoretical prediction, our three-variable VECMs show a robust substitution relationship between inbound FDI and imports, while the two-variable models do not.
This paper is organized as follows. The previous literature will be discussed briefly in section II. In section III, we will discuss the empirical model. Section IV describes the data and provides data analysis for the VECM. In section V, empirical results will be presented. Finally, section VI concludes.
1UNCTAD, World Investment Report 2004; www.unctad.org/fdistatistics 2IOM, World Migration 2005: Costs and Benefits of International Migration; www.iom.int 3Using product-level trade and FDI data, Blonigen (2001) finds that Japanese exports and Japanese production in the U.S. are substitutes. He identifies substitution effects from the vertical production relationship and points out the magnitude of the aggregation bias problem.
The theoretical connection between labor and capital movements has been studied in many papers. According to the simple classical two countries and two factors of production model, labor and capital will move where they can get the highest return under the assumption of the law of one price and identical technologies across different economic regions. In other words, capital moves from where the marginal product of capital is low to the place in which the marginal product of capital is high, while labor moves into the region where the marginal product of labor is high until the capital-labor ratio is equalized between two countries. Therefore, if the factors of production can move freely among the countries, they should move opposite to each other at the same time.
Such flows of factors in response to different factor prices, however, have not been supported by the empirical literature. On the one hand, international labor movements or immigration, seem to be consistent with theory if we ignore the political motives.4 A higher wage is seen as the main reason why people move across countries. However, there has been no strong evidence that capital moves opposite to labor simultaneously. In his 1990 paper, Lucas explains this empirical puzzle through human capital, labor quality, and capital market imperfection. Rich countries have more human capital than poor countries, and this immobile human capital makes rich countries more productive than poor countries. Therefore, capital moves into rich countries where productivity is high.
Groznik (2003) finds evidence against the classical equalization theorem that capital and labor should move opposite to each other. In addition, using aggregate data on U.S. annual net foreign direct investment flows and net migration flows from 1950 to 1997, he finds not only that labor and capital move in the same direction, but also that labor leads capital if capital is defined as FDI. In short, international labor movement is a forecasting indicator of FDI flows.
In addition to the classical trade theory literature, a recent literature on the importance of networks for international transactions is relevant for examining the relationships among trade, FDI, and immigrants. This literature suggests and finds evidence that interactions between people in the same ethnic groups in different countries can impact the international flow of economic variables. From a business perspective, ethnic networks strengthen the business link among the same ethnic people around the world. For example, Min (1990) finds a strong positive relationship between Korean immigrants to the U.S. and Korean exports to the U.S. market. Rauch and Trindade (1999) also find a significant positive effect of Chinese ethnic networks on bilateral trade between China and Southeast Asian countries. Girma and Yu (2000) focus on the relationship between immigration and trade in the case of the United Kingdom. They find that immigrants from former British colonies do not have a substantial impact on exports, while immigrants from other parts of world have a significant positive effect on exports. In his 2004 paper, Dunlevy epitomizes and shows the relationship between immigration and international trade through
In the case of international capital movements, Baker and Benjamin (1997) find no significant link between FDI and the stock of Asia-Pacific immigrants in Canada. In contrast, Gao (2000) shows that there is a significant positive effect of Chinese networks on inbound FDI in China.
However, none of these studies have considered the simultaneous effect of immigrant networks on trade and FDI. Therefore, there is a possibility that previous empirical research efforts on international movements of factors of production could be biased or misspecified owing to an endogeneity problem. Empirical research on international factor movements, including networking literature, has not considered the role of international trade on international factor movements. International factor movements clearly affect the domestic capital-labor ratio, so the domestic production structure could be affected in accordance with international factor movements. Consequently, movements of one factor of production can affect not only the movement of other production factors, but also international trade of goods and services. Furthermore, since factors of production are embodied in goods and services, the new international flow of goods and services could have serious consequences on the future international movements of factors of production.
In the case of empirical studies on the relationship between international trade and FDI, Lipsey and Weiss (1981) find a positive correlation between US outbound FDI and exports and suggest a potential endogeneity problem in their model.5 In their 1984 paper, Lipsey and Weiss use data on intermediate and final goods within firms and again find complementarity between affiliate production and exports of intermediate goods. Grubert and Mutti (1991) find a negative correlation between outbound FDI and export sales using similar data to Lipsey and Weiss (1981), but their findings are not statistically significant. Blonigen (2001) finds that Japanese exports and Japanese production in the U.S. are substitutes. He identifies substitution effects from the vertical production relationship and points out the magnitude of the aggregation bias problem.
However, none of these studies have considered the endogeneity which comes from the lack of information on international labor movements. Therefore, previous empirical findings may suffer from an endogeneity problem, and it could be the main reason why it has been so difficult to find the substitution effects between international trade and FDI.
4Vietnamese refugees and immigrants left Vietnam during the 1970s and early 1980s mainly for the freedom from Communism. There are more than one million Vietnamese living in the United States in 2000. 5The endogeneity comes from the characteristics of the host market.
The most efficient way to include all three endogenous variables – immigrants, inbound FDI, and imports - and examine their interactions is to use a vector autoregression (VAR) model. We consider a column vector of three variables and set a VAR model as our benchmark. We also estimate three different models with two variables representing previous major empirical findings, and then compare their results with three-variable VAR model’s results.6
As we show in the next section, since all three variables are non-stationary, it is necessary to consider cointegration and the error correction mechanisms. If time series are not stationary, then OLS regression could produce inconsistent estimates. However, even though each individual time series is non-stationary, the deviation between or among variables could be stationary. In other words, if variables move together, the level specification will not suffer from an inconsistency problem. In fact, the estimated parameters will be super-consistent, which means that the consistency will be held even though the errors of the regression are correlated serially or correlated with regressors.
The error correction mechanism corrects short run disequilibrium and hence it gives a distinction between short run and long run multipliers. The Granger representation theorem states that if variables are cointegrated with each other, then their relationships can be expressed as an error correction model. In their seminal paper, Engle and Granger (1987) introduce a famous two-step method to build an error correction model: first, run a cointegrating regression and test its residuals for stationarity, second, if the residuals are stationary, then use those residuals as an explanatory variable in the error correction model.
Long-run parameters from the two-step method, however, could be biased if a cointegrating regression is misspecified. This misspecification problem occurs when OLS estimation confronts more than one possible normalization. Johansen (1988, 1991) introduces a maximum likelihood method which overcomes this normalization problem. Johansen’s method can analyze both short run and long run properties efficiently. We follow Johansen’s procedure to find the proper cointegration vector and the equilibrium equation.
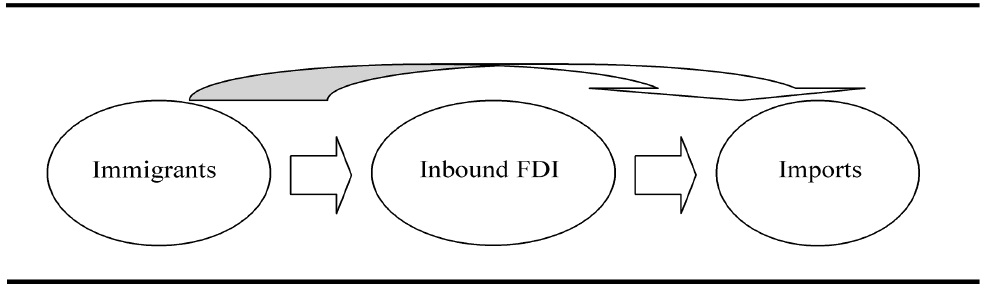
We consider a column vector of three variables – immigrants, inbound FDI, and imports – and set a VAR model. The econometric specification is motivated by existing theories on the international movements of factors of production. Based on research related to networks effects, we assume that immigration (international labor movements) could lead to a change in both international capital flows and international trade. For the econometric specification, the variable representing international labor movements will be treated as the most exogenous variable in the VAR model.
Since capital is defined as FDI, we consider the link between FDI and international trade to decide the order between the two variables. Based on existing FDI literature, we assume that FDI is one of the main factors driving international trade. According to theories on multinational firms, such firms can be classified into two different groups, horizontal and vertical. Horizontal multinational firms can be explained by the concept of economies of scale at the firm level and the desire to avoid trade frictions. A horizontal multinational firm has several plants around world, and produces basically identical or very similar products in each plant. Therefore, theories predict that FDI substitutes for international trade if FDI is performed by the horizontal multinational firm.
Vertical multinational firms, on the other hand, can be understood by classical relative factor endowment differences. Firms who use labor intensively can take advantage of relatively cheap labor costs if they build their plants in the labor abundant country. Multinational firms can separate their facilities by production stage among different countries. For example, multinational firms can build their headquarters or R&D institutions in the capital or human capital abundant country and build their plants in the labor abundant countries. In this vertical FDI case, FDI can generate an international trade flow.
Either horizontal or vertical FDI activities can affect international trade flows, so we assume that inbound FDI is a cause of import flow fluctuation. Therefore, the imports variable is treated as the most endogenous variable in the VAR model. Figure 2 indicates the Choleski order among the three variables in the model.
Our basic VAR(2) model can be written as
and Y´t = [ immt fdit impt ].
Replacing Yt-2 by Yt-1 – ΔYt-1, then equation (1) can be equivalently be written as
Subtracting Yt-1 from both sides of equation (2), then equation (2) can be written as equation (3), which is the error correction representation of the cointegrated system.
where Π = (I – Φ1 – Φ2) = – αβ´, ζ = – Φ2 and β´ is the cointegration vector.
The multiplier matrix is a lower triangular and the Choleski decomposition is used to identify restrictions.
6The three models are immigrants and inbound FDI, immigrants and imports, and inbound FDI and imports.
Ⅳ. Data Description and Analysis
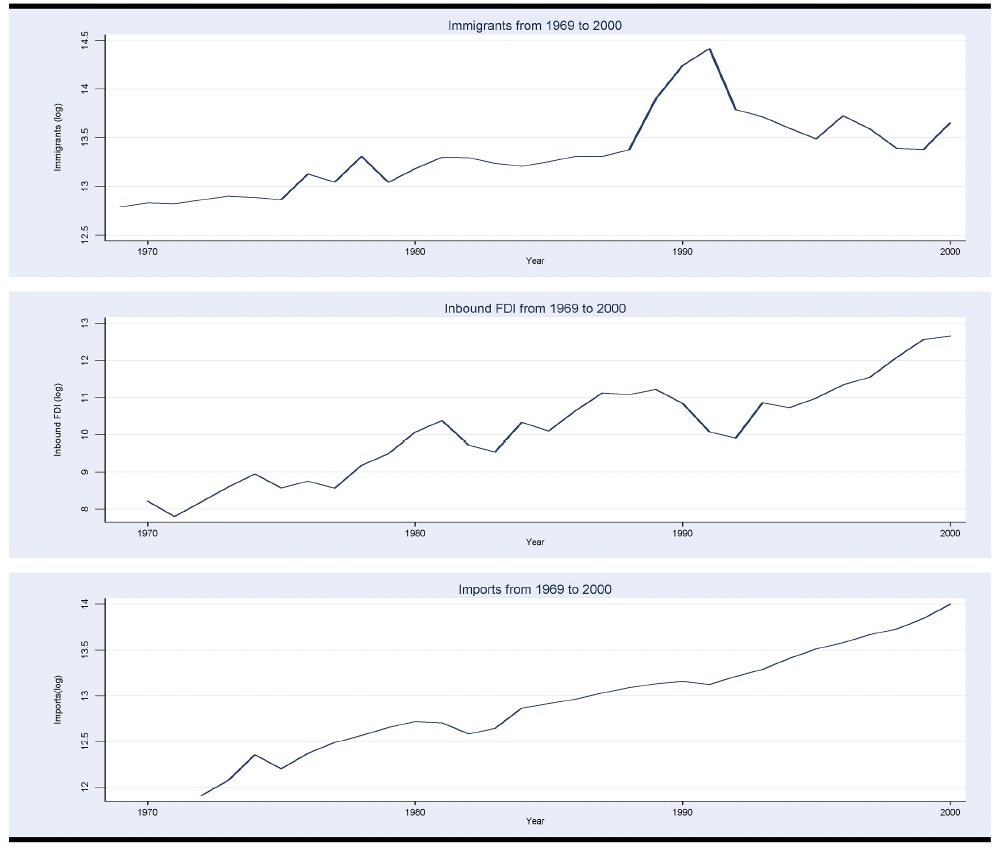
The variables considered in the VECM are immigrants (immt), inbound FDI (fdit), and imports (impt). All estimates presented in this paper are based on annual U.S. data from 1969 to 2000. The immigrant data are the number of immigrants from the foreign countries into the U.S. from 1969 to 2000. These data are a flow variable and available in the ‘Yearbook of Immigration Statistics .’7 We do not consider illegal immigration because there is no source to estimate the number of illegal immigrants sorted by origin countries and years. If we assume that most illegal immigrants are unskilled labor, ignoring illegal immigrants could bias immigrants toward being overly skilled. The import data are the customs value of the U.S. annual imports and available from the NBER database.8 The inbound FDI data used in our VECM are annual FDI inflows from the rest of the world into the U.S. and available in an UNCTAD database.9 Both imports and inbound FDI are measured in 1996 dollars.
Figure 3 shows the movements of each variable from 1969 to 2000. All three variables show upward trends during the period, which is strong evidence for the existence of non-stationarity in the variables.
Table 1 presents test statistics from the augmented Dickey-Fuller test for unit roots. It clearly indicates that we cannot reject the null hypothesis of a unit root for all three variables even at the 10 percent level of significance. Since all three variables are non-stationary, we consider cointegration and the associated error correction model.
[Table 1] Augmented Dickey-Fuller Test for Unit Root

Augmented Dickey-Fuller Test for Unit Root
Cointegration and VECMs
To test whether variables are cointegrated or not, we perform the Johansen cointegration test. To carry out the Johansen cointegration test, we assume that the trend term is restricted to appear only in the cointegration equation. Table 2 shows that the trace statistic indicates that one cointegrating relation exists at the 5 percent level of significance.
[Table 2] Johansen Tests for Cointegration

Johansen Tests for Cointegration
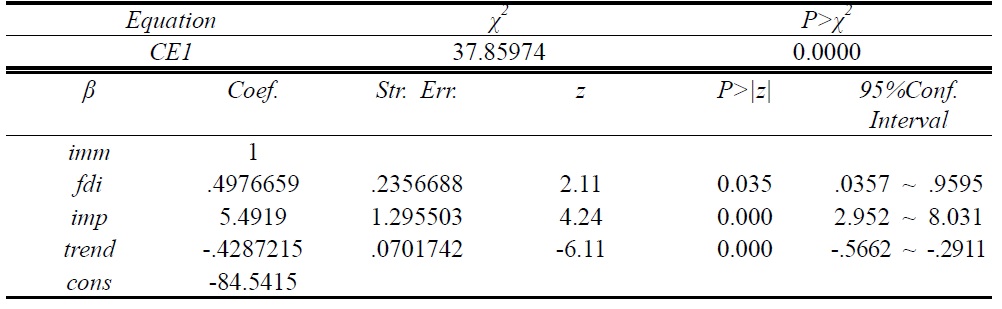
To avoid the normalization problem, we follow Johansen’s maximum likelihood method to get a proper cointegration vector and an equilibrium equation. Table 3 presents a cointegration vector and an equilibrium equation.
[Table 3] Cointegration Equations
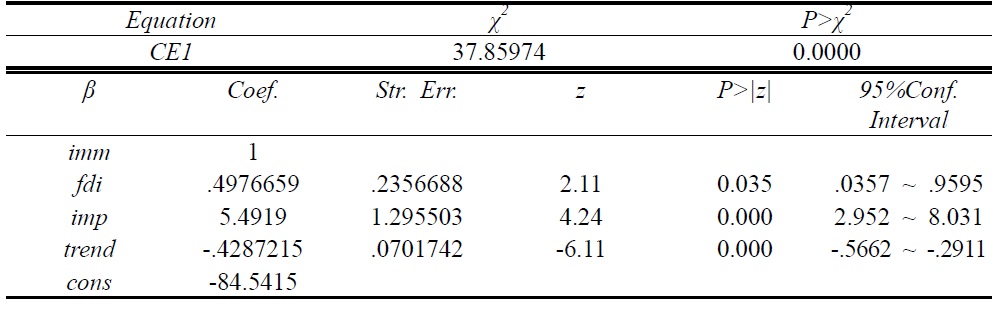
Cointegration Equations
7Formerly, before the 2002 edition, this data source was entitled Statistical Yearbook of the Immigration and Naturalization Service. The first edition was published in 1978 and it covers immigration data from 1969 to 1978. 8International Trade Data, U.S. Imports by TSUSA, HS, SITC, 1972-2001; http://www.nber.org/data 9UNCTAD´s Division on Investment, Technology and Enterprise Development; http://www.unctad.org
VECM with three variables: Immigrants, Inbound FDI, and Imports: Y´t = [ immt fdit impt ]
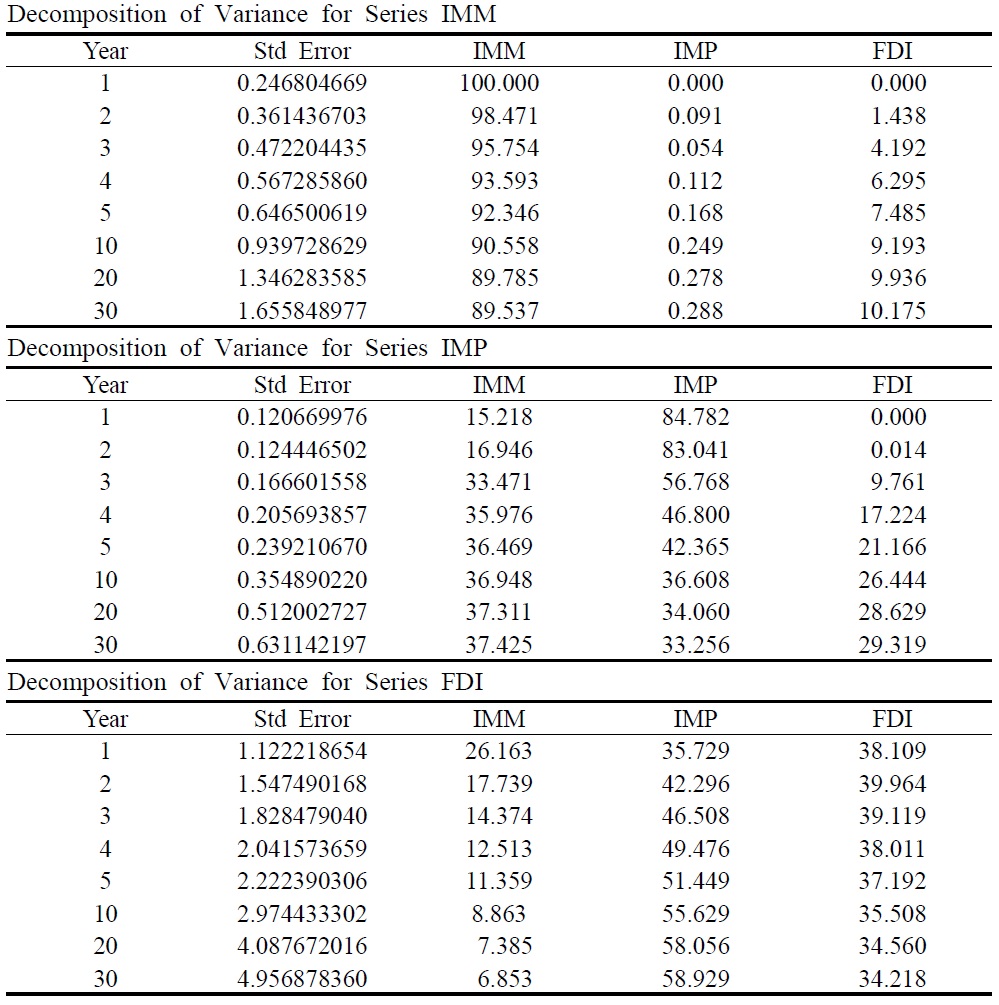
We estimate a vector error correction model in equation (3) using two lags of the variables with a constant and an error correction term. First of all, we use variance decompositions to identify the causal relation among the three variables. In addition, impulse response functions display the response of three variables to shocks in each variable. Results from both variance decompositions and impulse response functions jointly determine the relationship between inbound FDI and imports.
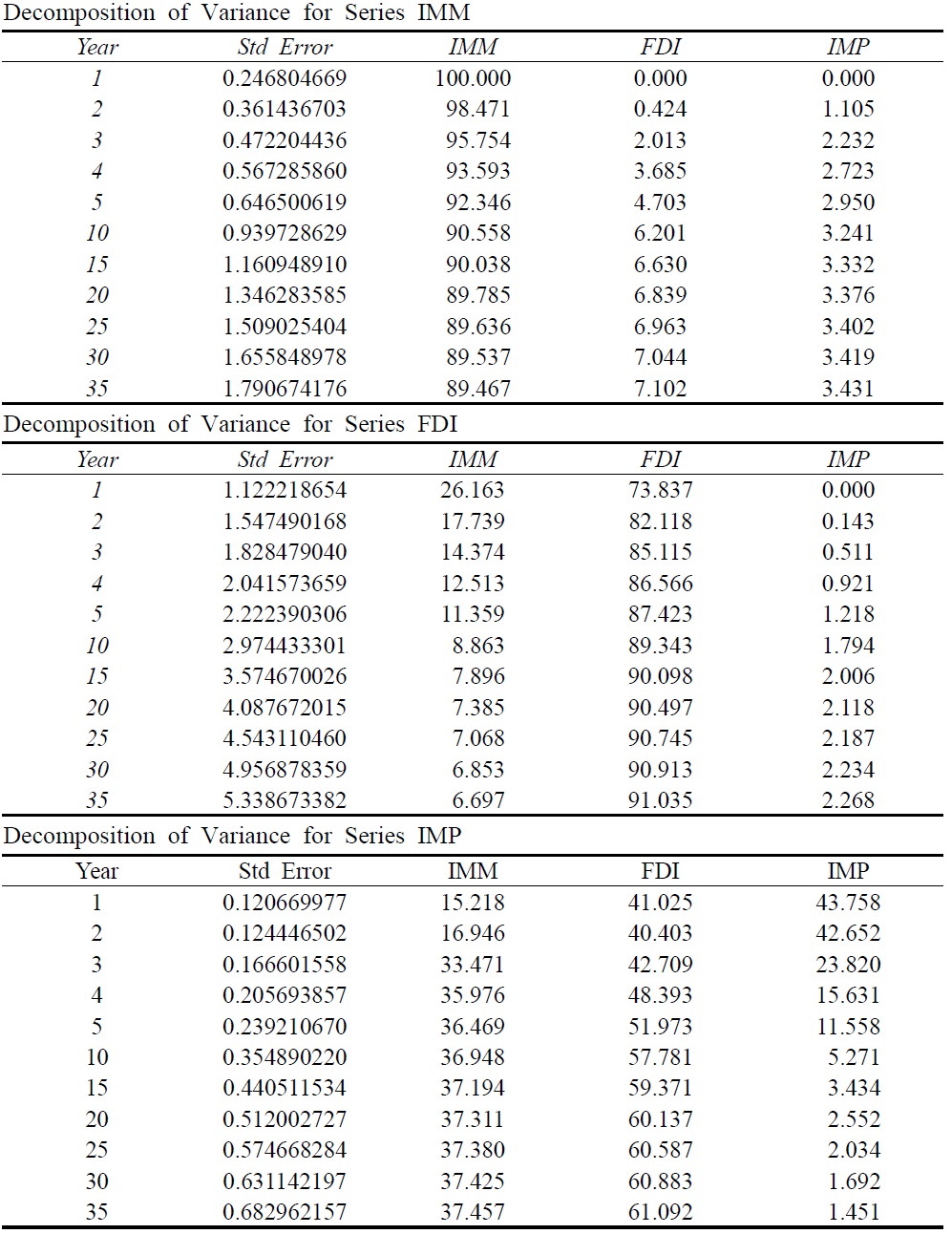
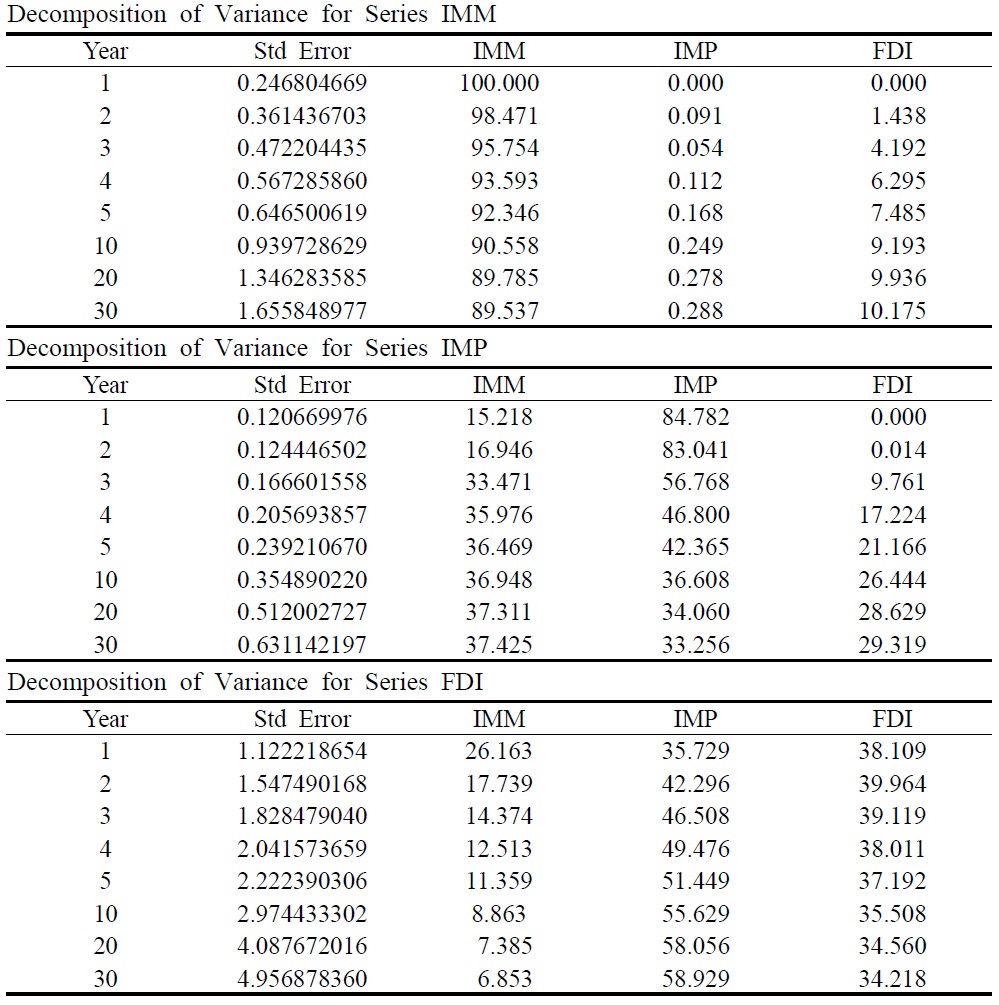
Table 4 contains the variance decompositions for each variable. The table shows the fraction of the variance of the forecast error for each of the variables. For the immigration variable, the main factor which drives immigration is its own past, not only in the short run, but also in the long run. The inbound FDI variable has some explanatory power for the fluctuation of immigrants, but it is hard to say that FDI has a substantial effect on immigration because the magnitude of the effect is quite small. Imports do not have any explanatory power for immigration over the time period.
In the case of FDI, the inbound FDI variable is the main source of its own fluctuations. Immigration explains 26 percent of the variability in the first year and maintains its substantial explanatory power for 5 years. Even after 10 years, immigration explains 9 percent of the variability. Therefore, immigrants can be considered a factor causing inbound FDI in the short run. Imports do not have any substantial explanatory power for FDI variation.
For the imports variable, the main factor driving imports is its own past for the first two years. After 2 years, FDI becomes the principal mover and sustains its explanatory power for imports in the long run. Immigration also has a substantial explanatory power over the time period. After 5 years, both immigrants and inbound FDI explain at least 95 percent of the variability of imports, hence, both immigrants and inbound FDI can be considered as causal factors for imports.
In short, the variance decompositions suggest the following. First, immigrants have a substantial explanatory power for both imports and inbound FDI. Second, inbound FDI is the principal mover of imports after 2 years. Third, imports have a negligible explanatory power for both inbound FDI and immigrants.
[Table 4] Decomposition of Variance
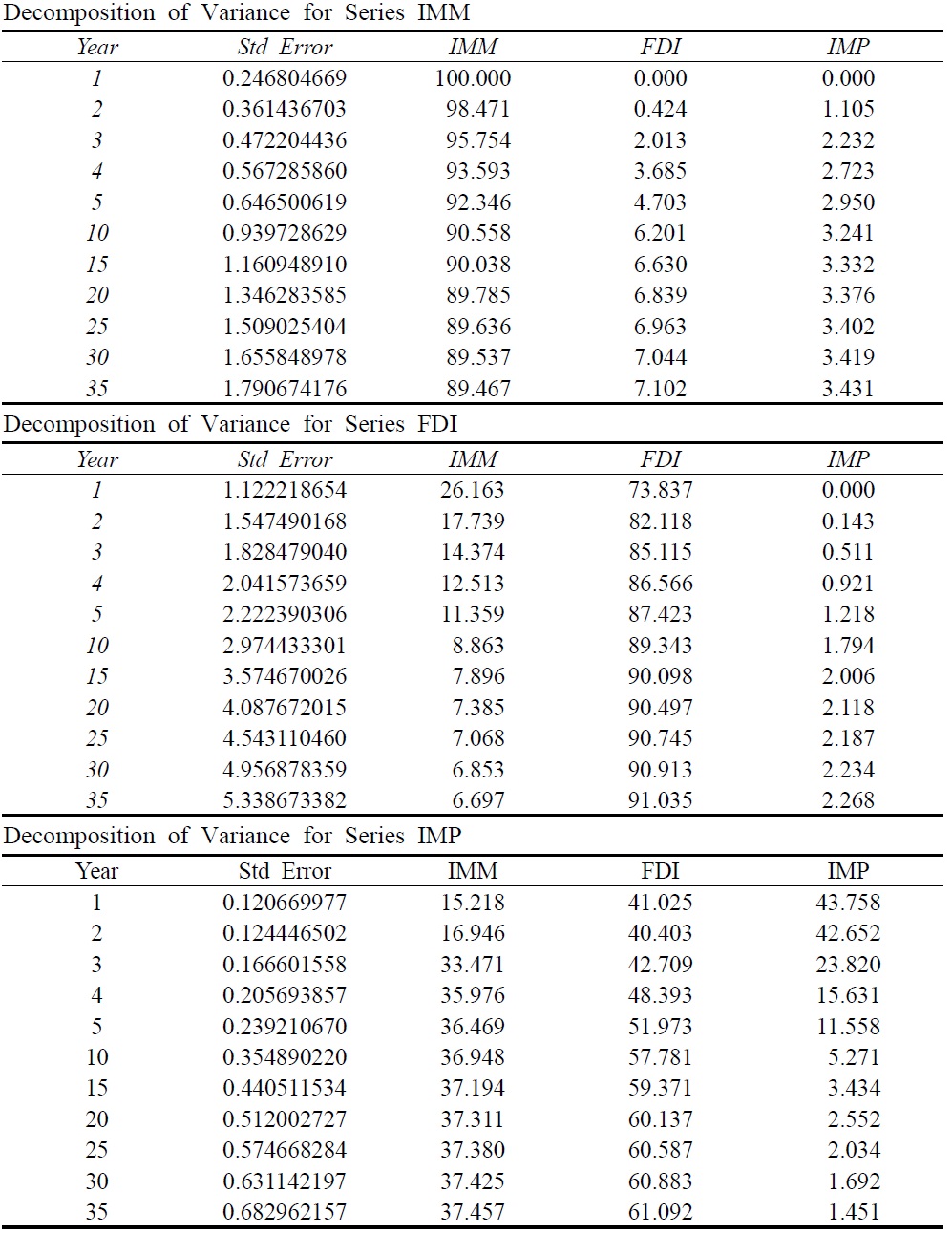
Decomposition of Variance
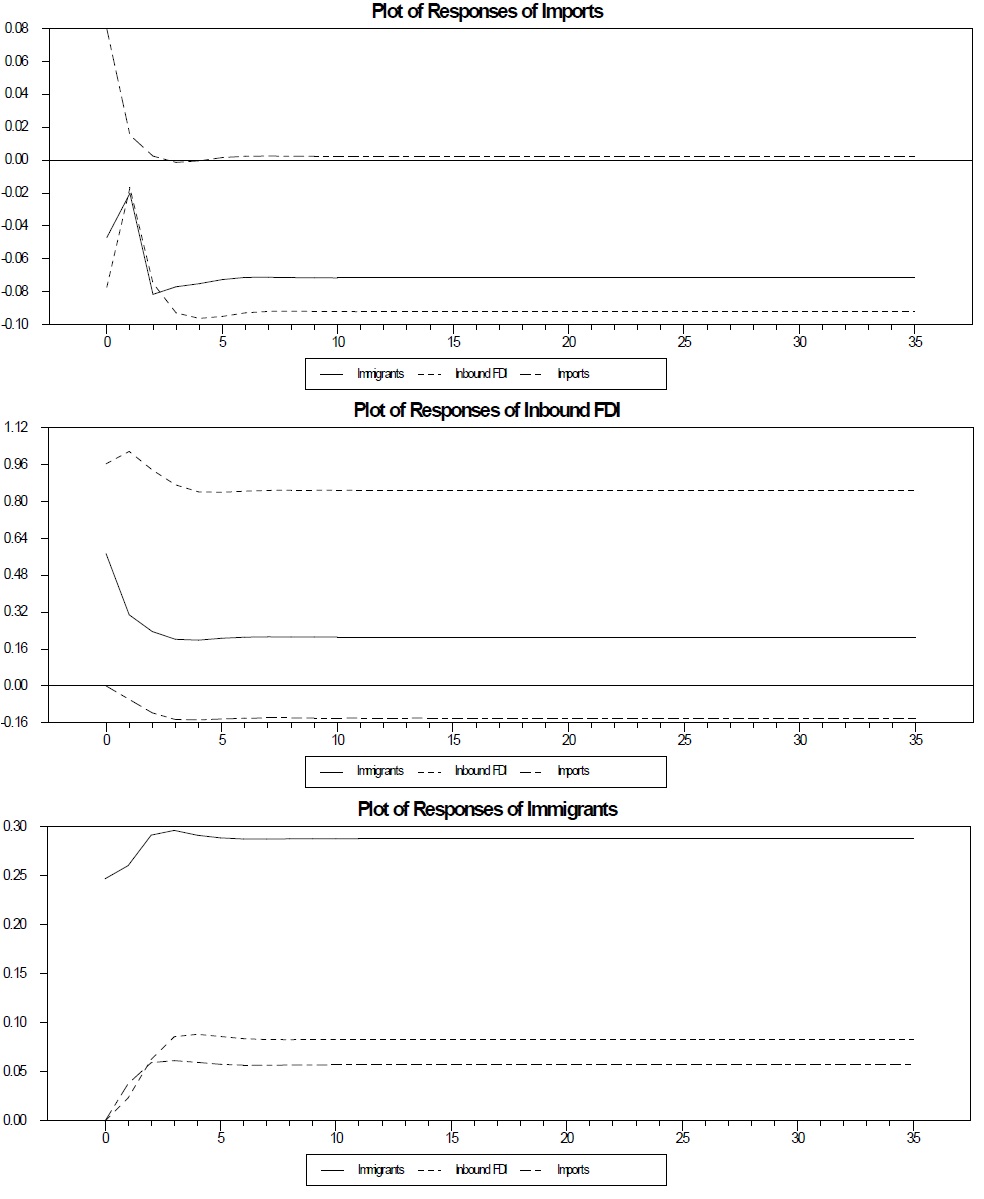
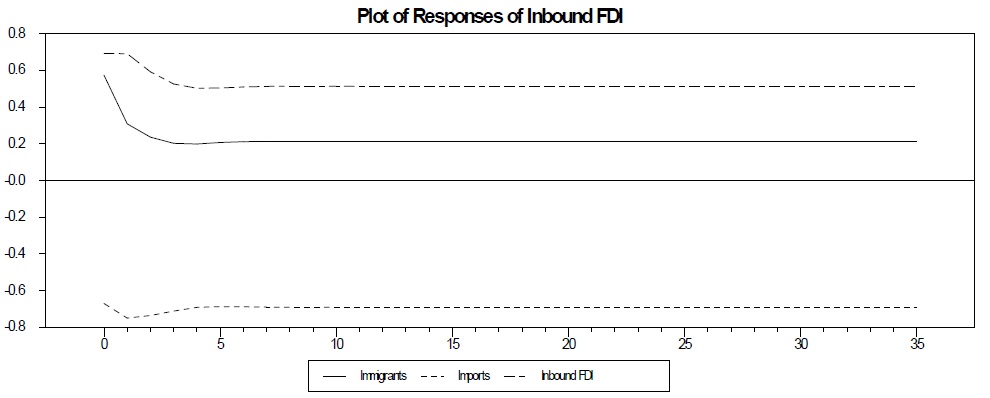
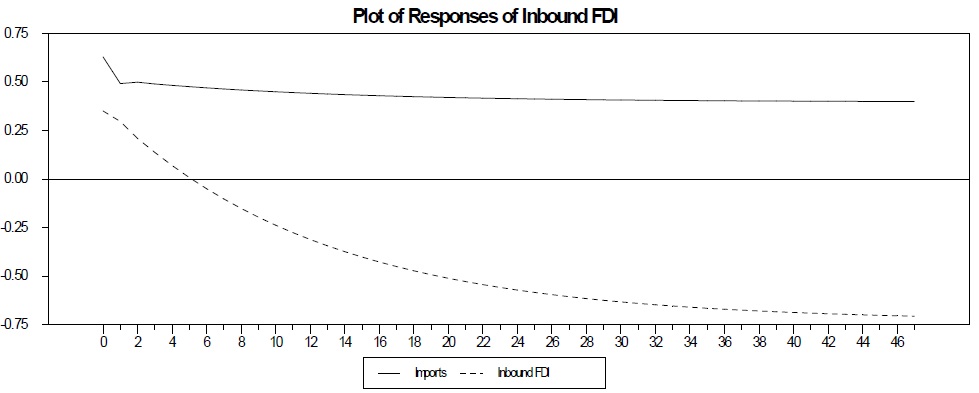
Figure 4 displays the response of the logs of immigrants, inbound FDI, and imports to shocks in each variable. These graphs show the differences between the two-variable and three-variable VECM. In the first graph, regarding the dynamic response of imports to a shock to each endogenous variable, imports respond negatively to a shock in inbound FDI and there is a level effect. This finding clearly suggests a substitution relationship between inbound FDI and imports. Since most of inbound FDI for the U.S. is carried out by horizontal multinational firms, these substitution effects accord with the theoretical prediction.
The second graph, showing the plot of responses of inbound FDI, clearly reveals that immigrants and inbound FDI are complements. Inbound FDI responds positively to a shock in immigrants and there is a level effect as well. Therefore, results from the variance decompositions and impulse response functions imply that immigrants lead inbound FDI for the U.S. and these variables are complements to each other.
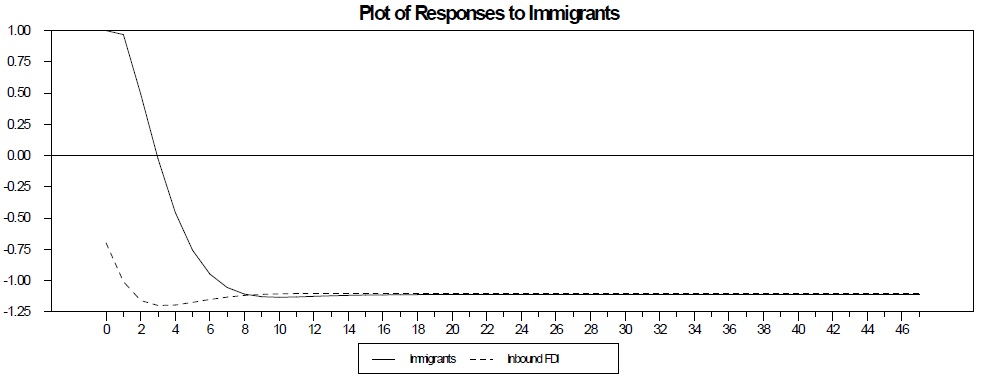
The last graph, displaying the responses of immigrants to shocks, indicates that immigrants respond positively to a shock to itself in that immigrants today will increase immigrants tomorrow. In the case of the two-variable model, as we show in the next section, the positive effect of a shock to immigrants on itself disappears after 3 years. Furthermore, immigrants have a negative level effect on itself in the long run, which is not supported by the fact that immigrants have increased during the last three decades.
Does Ordering Matter? : Y´t = [ immt impt fdit ]
To test the robustness of our findings, we consider an alternative ordering between inbound FDI and Imports. We assume now that imports lead inbound FDI in the three-variable model. Figure 5 and Table 5 show that our main results remain unchanged except for the fact that imports now have explanatory power for the fluctuation in inbound FDI.
Immigrants lead both inbound FDI and imports. Immigrants and inbound FDI are complements, while imports and inbound FDI are substitutes. The alternative ordering between inbound FDI and imports does not alter the correlation among the three variables.
VECMs with two variables
To compare previous findings with our VECM analysis, we now consider three different two-variable VECMs representing major previous empirical research: Y´t = [ immt fdit ], Y´t = [ fdit impt ], and Y´t = [ impt fdit ]. We follow similar methodologies and variable orderings for these two-variable VECMs.
[Table 5] Decomposition of Variance
Decomposition of Variance
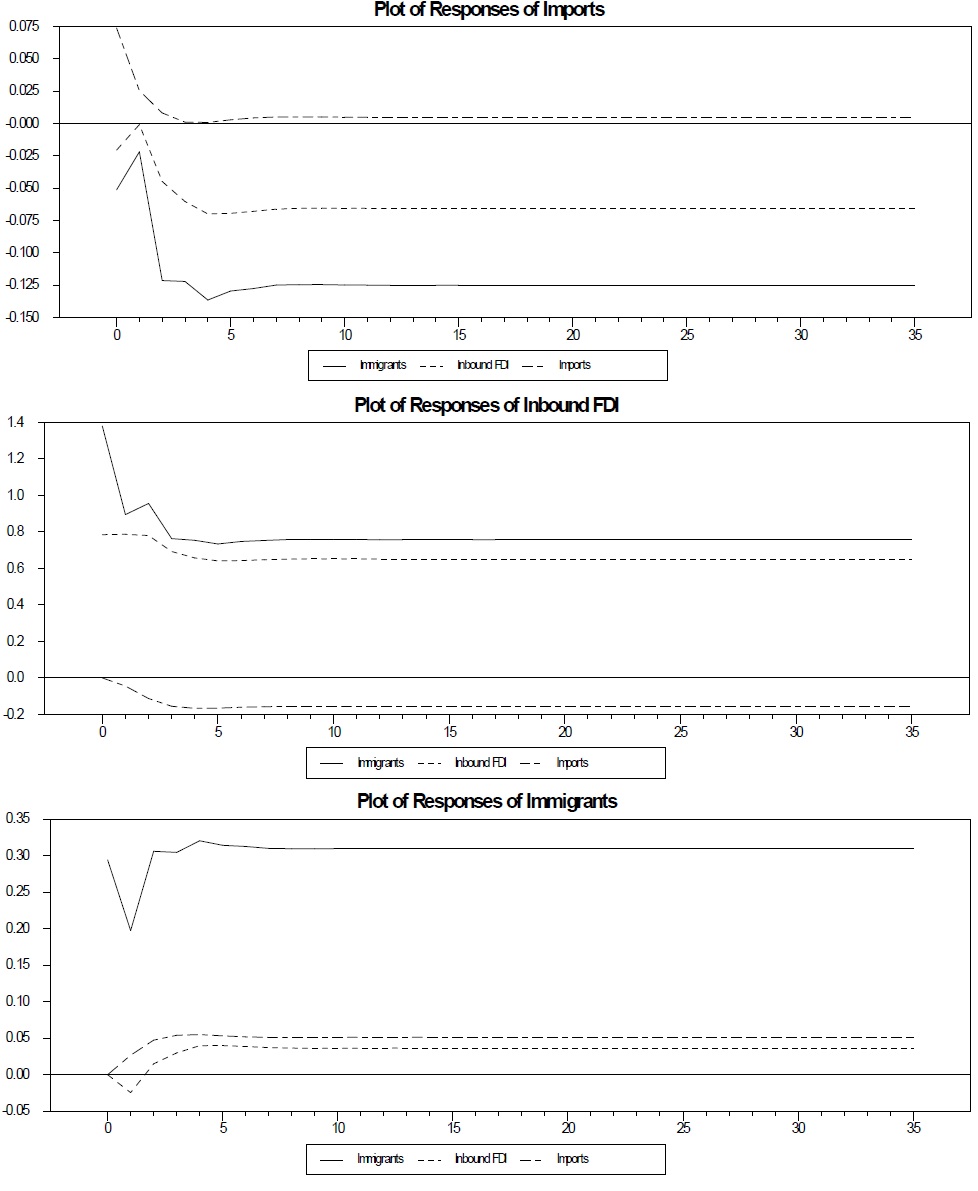
For brevity, we only discuss two main differences between the results of these two-variable VECMs and the three-variable VECM presented above. First, Figure 6 shows the two-variable immigrants-inbound FDI VECM and suggests that immigrants are substitutes for inbound FDI, which coincides with the prediction of neoclassical trade and growth theories. However, this is contrary to the prediction of the networks effect literature and our findings with the full three-variable VECM. This highlights the bias from not considering all three variables simultaneously.
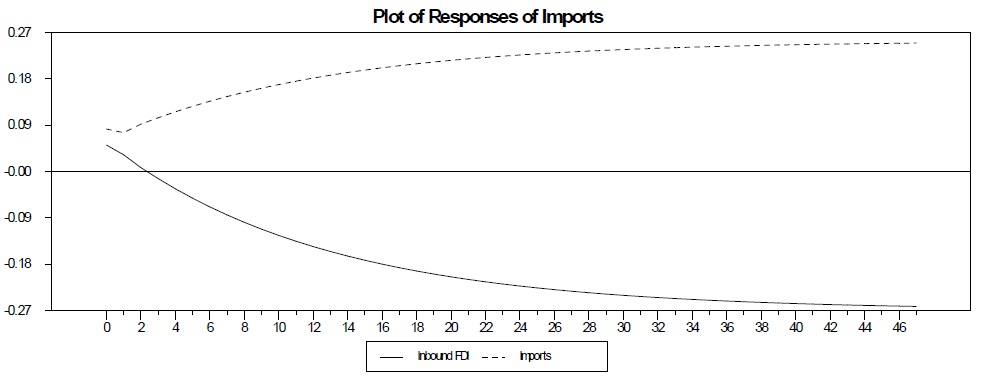
Second, ignoring international labor movements leads to ambiguous results in the relationship between FDI and international trade. Figure 7 and 8 show a clear example of the omitted variable problem. Without considering the immigrants variable, Figure 7 displays the response of the imports to shocks in both inbound FDI and imports from the model assuming that inbound FDI generates imports. This graph shows that imports respond negatively to a shock in inbound FDI and there is a level effect. This finding suggests a substitution relationship between inbound FDI and imports, which is similar to our findings with the full three-variable VECM.
On the other hand, the model assuming that imports cause inbound FDI without considering the immigrants variable shows a complementarity relationship between imports and inbound FDI. Figure 8 clearly indicates that inbound FDI responds positively to a shock in imports, and is similar to those of other previous existing analyses. Therefore, the ordering between inbound FDI and imports in a two-variable VECM matters for the direction of the response. This sensitivity of empirical results in the case of a two-variable VECM could come from the omission of the immigrants variable.
Analysis without Mexican data
We do not consider illegal immigrants because there is no source to estimate the number of illegal immigrants sorted by origin countries and years. Ignoring illegal immigrants, however, could bias the impact of immigrants on both inbound FDI and imports. To test the robustness of our findings, we present a VECM without Mexican data.
Figure 9 displays the response of the logs of immigrants, inbound FDI, and imports to shocks in each variable. Compared to the main findings with Mexican data, the results basically remain the same and confirm that imports and inbound FDI are substitutes. The alternative specification does not alter the correlation among the three variables.
This is the first study to simultaneously consider interactions of three major international variables: immigrants, inbound FDI, and imports. In testing the patterns of international movements of factors of production, most existing research has omitted the role of international trade. On the other hand, research on the relationship between FDI and international trade has neglected the importance of international labor movements. In this study, we use a vector error correction model to include all three major international variables in a model. Using the U.S. annual data from 1969 to 2000, we find that labor and capital move in the same direction and labor causes capital.
In addition, we also find that inbound FDI and imports are substitutes. This substitution relationship between inbound FDI and imports is predicted by theory, but has not been supported by empirical work, especially in the case of country level data. In the case of cointegration, estimated parameters are super-consistent, which means that the consistency will be held even though the errors of the regression are correlated serially or correlated with regressors, hence there is no endogeneity problem in a vector error correction model. Therefore, it is possible that previous empirical research analyses, which have found complementarity relationships, could have suffered from the endogeneity problem because their empirical results are not based on the error correction model.
To identify the impact of immigration on imports and inbound FDI, we simplify our empirical model and consider only three major endogenous variables. This simplification motivates an obvious extension to examine the other variables being left out of analysis. In particular, the lack of some core macroeconomic variables, such as foreign exchange rate and interest rates, could also be a source of misspecification problem. This extension requires a new structural model to induce the reduced form equations. Therefore, it is necessary to consider the dynamics between the new macroeconomic variables and existing three endogenous international variables, which is a subject for further study.