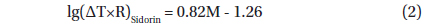Questions about earthquake precursors are becoming increasingly important due to increasing seismic activity in different regions of the Earth. Many earthquake precursors involving significant deviations in parameters of various geophysical fields in the lithosphere, lower atmosphere, and ionosphere have so far been identified (Zubkov & Migunov 1975; Sidorin 1979; 1992; Liperovsky et al. 1992; Gufeld & Gusev 1998; Korsunova & Khegai 2006, 2008). Moreover, in recent years anomalies of the total electron content (TEC) in different seismically active areas have been extensively examined with the aid of satellites (Sarkar et al. 2007; Saroso et al. 2008).

Regularities of the appearance of precursors for earthquakes with different energetic characteristics have been studied. The time of precursor occurrences has been shown to depend on the magnitude of a forthcoming earthquake and on the distance from the epicenter (Sidorin 1979; Zubkov 1987; Korsunova & Khegai 2008). Ionospheric precursors can be identified only with some degree of probability owing to the strong variability of the ionosphere because a considerable portion of ionospheric anomalies is not followed by earthquakes, even under quiet geomagnetic conditions (Perrone et al. 2010; Kwak et al. 2014; Kil 2015). To assess the reliability and significance of probable earthquake precursors discovered in the ionosphere, the authors of Chen et al. (2004) have proposed to evaluate the effectiveness of the existing method for identifying ionospheric precursors by variations in the critical frequency of the F2 layer (foF2). The existing method appears sufficiently effective for strong earthquakes with M > 5.5, but ineffective for weaker earthquakes since, in these cases, the foF2 variations rarely exceed the amount of random deviations.

We have put forward another method for detecting ionospheric earthquake precursors, taking into account several key parameters of the sporadic E layer (h'Es, fEs) and an additional parameter of foF2 (Korsunova & Khegai 2006, 2008). This method allowed us to identify ionospheric precursors for weaker earthquakes at a considerable distance from the epicenter. However, we have not evaluated the effectiveness of this method in such cases. This question is discussed in this paper based on earthquake data from NEIC USA (http://www.earthquake.usgs.gov) and on vertical sounding ionospheric measurements made in PetropavlovskKamchatsky, which were taken from NGDC USA (http://www. ngdc.noaa.gov).

The proposed method for identifying possible ionospheric earthquake precursors is based on the correspondence between anomalous changes in a number of ionospheric parameters and a particular set of morphological characteristics of ionospheric behavior, which were revealed by long-term studies during preparation of earthquakes of different magnitudes in diverse seismically active areas. Under this method, ionospheric earthquake precursors are characterized by the following:

- the appearance of abnormally high sporadic E layer (Es) exceeding background values of virtual heights (h'Es) in quiet geophysical conditions at a specific time of day over values of not less than 10 km for 1-3 hr; - an increase in Es characteristic frequencies by no less than 20 % accompanied by a rise in foF2 over the same duration within a daily time interval of ±12 hrs relative to the appearance of the abnormally high Es.

Notice that the scope of the method is naturally limited by the latitudes, which quite often exhibit the midlatitude sporadic E layer obeying the already well-known diurnal and seasonal patterns (Chavdarov et al. 1975). For Petropavlovsk-Kamchatsky (geographical coordinates of the ionosonde φ = 53.02 ºN; λ = 158.65 ºE), this occurs mainly during the summer months. Therefore, we processed ionospheric data for August 1998, June-August 1999, July 2000, May-June and August-September 2001, and April-May 2002. Possible ionospheric earthquakes precursors were selected as follows:

- we calculated deviations of current values of Es virtual heights (∆h'Es), Es blanketing frequencies (∆fbEs), and critical frequencies of the F2 layer (∆foF2) from the average values of these parameters during geomagnetically quiet days (Ap ≤ 10-15 nT); - we determined days during which deviations in all the three parameters met the criteria for selection of ionospheric precursors, i.e. ∆h'Es ≥ 10 km, ∆fbEs/(fbEs)averages ≥ 20 % and ∆foF2/(foF2)average ≥ 10 % for t = 1-3 hrs.

In 38 cases, for the selected months, we discovered anomalies in the Es and F2 layers, which fulfill the criteria for selection of ionospheric earthquake precursors. In 29 cases, with different delay time (∆T), these anomalies were followed by M = 4.6-6.0 earthquakes, which occurred at epicentral distances (R) of 100-400 km from the observation point. During the observation period (323 days) considered, there occurred 34 earthquakes with the indicated magnitudes; at the same time, in 9 cases, under quiet geomagnetic conditions, there were anomalies in Es, which were not followed by earthquakes in the above range of magnitudes; therefore, these cases were classified as "false alarms".

For all the chosen ionospheric anomalies, there is a tendency for the earthquake precursor lead-time to vary depending on earthquake magnitude and epicentral distance to an observation point. The higher the magnitude, the earlier the precursor appears for the same R, i.e. the longer the earthquake precursor lead-time ∆T. At increasing R and equal M, the earthquake precursor appears later. Such behavior is typical of medium- and long-term earthquake precursors and implies disturbance propagation from an epicenter to the boundaries of an earthquake preparation zone (Gufeld & Gusev 1998).

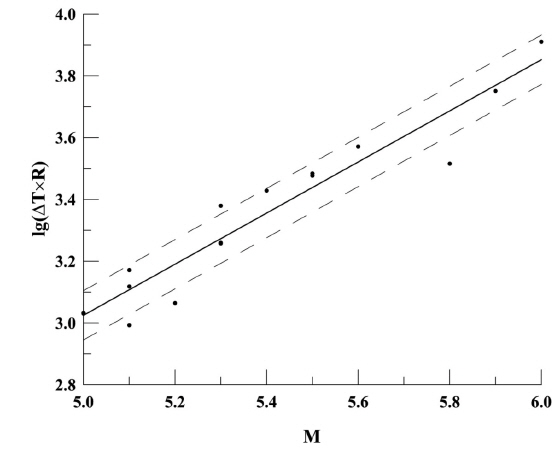
For 16 earthquakes (with M = 5.0-6.0), Fig. 1 illustrates variations in the lead-time for earthquakes (∆T) distinguished by possible ionospheric precursors (dark circles) depending on the magnitude of subsequent earthquakes and epicentral distance. The linear regression,

obtained with the least square method, is indicated by the solid line in Fig. 1 with corresponding standard deviations (dashed lines).

The standard regression error is S_lg(∆T×R) = 0.08. The correlation coefficient for the 5 % level of significance according to the Student's t test for the selected 16 cases is ρ= 0.96 with a confidence interval of 0.92-0.99. Both the regression coefficients are statistically significant; the standard deviation of the coefficient determining the slope of the regression line is 0.07, and the standard deviation of the free term is 0.35. Our analysis shows that despite the limited number of selected cases, the estimated correlation coefficients suggest a sufficiently high degree of reliability of the obtained relationships between the earthquake precursor lead-time and earthquake magnitude for specific epicentral distances.

A similar dependence has been found in Sidorin (1979) from measurements of different physical parameters in the earth's crust, which were made in the same seismicallyactive area but in other years (geodetic measurements, electrotelluric field, groundwater level, slopes of the earth's surface, deformations, seismic-wave velocities):

The numerical coefficients in Formula (2) fall into the range of coefficients of Formula (1) in accordance with their standard deviations. This indicates an increase in the reliability of the identification of ionospheric precursors of earthquakes by the above procedure.

The fundamental difference of the method we use (Korsunova & Khegai 2008) is that it considers several parameters characterizing the state of the lower and upper ionosphere. This improves the reliability of identification of pre-earthquake ionospheric anomalies just as earthquake precursors, but does not rule out errors associated with the occurrence of false precursors ("false alarms"), which are not followed by earthquakes. Such cases have been found before by similar studies performed in Italy (Perrone et al. 2010) and in the Kamchatka region (see above, Section 2). Thus, a need arises to evaluate the effectiveness of the method for identifying ionospheric earthquake precursors.

Chen et al. (2004) proposed several ways of determining the effectiveness of a particular method for identifying earthquake precursors from empirical data in back calculations. Yet a contingency table is compiled for a chosen observation interval; days are put in a 2×2 matrix according to their characteristics, and then some assessment of quality of identification of possible earthquake precursors is used as if the prediction was made based on their occurrence.

One of these assessments (Chen et al. 2004) is the socalled Hanssen-Kuipers Score (True Skill Statistic, Pierce Skill Score, Rscore), which in our consideration, is the difference between the probability of detecting a true earthquake precursor and the probability of detecting a false precursor. Its value may range from -1 to 1 where the latter means 100% probability of detecting a true precursor without false alarms. This assessment is given by the following expression:

where "a" is the number of days with alarms followed by earthquakes (correct prediction, "hit the mark", an earthquake occurs), "c" is the number of days with earthquakes without alarms ("miss the mark"), "b" is the number of days with alarms that were not followed by earthquakes ("false alarms"), and "d" is the number of days without alarms and earthquakes (correct prediction that the "mark" (earthquake) will not occur). In this study, we have analyzed 323 days of ionospheric observations, during which 34 earthquakes with M = 4.6-6.0 occurred. For the time intervals considered, it appears that a = 29, b = 9, c = 5, and d = 280. Then from (3), it follows that Rscore = 0.82. This suggests that our method for identifying ionospheric earthquake precursors by simultaneous measurements of several parameters of the Es and F2 ionospheric layers is sufficiently effective.

The investigation of ionospheric effects followed by M= 4.6-6.0 earthquakes determined from Es and F2 parameters, measured using the vertical sounding ionosonde in Kamchatka with an interval of 1 hr, leads to the following conclusions.

1. The logarithmic dependence connecting earthquake magnitude, earthquake precursor lead-time, and distance from the observation point to the epicenter, which was obtained from ionospheric data, corresponds to the analogous dependence for earthquake precursors, which was derived from measurements of different ground geophysical parameters at the same seismically active area.

2. The method for identifying ionospheric precursors of earthquakes, which relies on the analysis of deviations of the virtual height of the sporadic E layer, Es blanketing frequency, and the critical frequency of the regular F2 layer, is characterized by sufficiently high effectiveness.