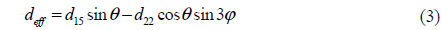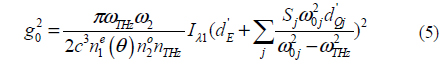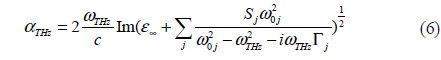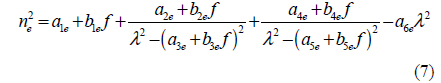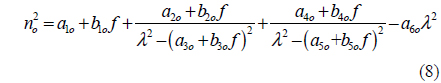In the study of modern terahertz (THz) optoelectronics, monochromatic THz sources play an important role in high resolution THz applications, such as environmental gas monitoring and high-density and high-speed wireless communications [1-4]. Difference frequency generation (DFG) with two closely spaced laser frequencies ω₁ and ω₂ in second-order nonlinear optics crystals is one of the promising processes for efficient monochromatic THz wave output in the wide frequency tuning range and for room temperature operation [5, 6]. Recently, high-efficiency THz wave generation based on DFG employing Cherenkov phase matching has been intensively researched [7-9]. THz wave generation with Cherenkov phase matching is an attractive scheme because strong THz absorption originated from lattice vibration modes of the nonlinear optical crystal can be overcome. Unfortunately, the maximum frequencies generated by DFG with a Cherenkov phase matching scheme are limited to 7.2 THz [10]. Moreover, the output power of the THz wave within the high-frequency band is extremely low. Such limitations on output frequencies and power are caused by the dramatically increased absorption of the nonlinear materials in the vicinity of polariton resonances. However, at the same time, polariton resonances can induce giant second order nonlinearities [11-13]. The giant second order nonlinearities in the vicinity of polariton resonances can be exploited to extend the output frequencies and enhance the output power of the THz wave. In this paper, we explore THz wave generation based on DFG in the vicinity of polariton resonances with a Cherenkov phase matching scheme. A surface-emitted configuration is employed to overcome the strong absorption problem in the vicinity of polariton resonances. The nonlinear crystals utilized in this paper are bulk and periodically poled LiTaO₃ (PPLT). To the best of our knowledge, THz wave generation based on DFG utilizing bulk LiTaO₃ and PPLT with a Cherenkov phase matching scheme has not been investigated. The advantage of utilizing LiTaO₃ over LiNbO₃ lies in the fact that LiTaO₃ has a significantly reduced rate of optically-induced index change damage due to the photorefractive effect [14]. According to Ref. [14], the optically induced index-change damage increases at rates of 2.8×10⁻³ cm²/μW and 4.9×10⁻⁴ cm²/μW in LiNbO₃ and LiTaO₃, respectively. The second advantage is that the poling electric field required for LiTaO₃ is one order of magnitude lower than that for LiNbO₃ [15]. The coercive fields are 1.7 kV/mm and 21 kV/mm for stoichiometric LiTaO₃ and congruent LiNbO₃, respectively [15]. In this paper, a Cherenkov phase matching scheme is realized by using the crystal birefringence of bulk LiTaO₃ and a grating vector of PPLT. We numerically simulate the frequency tuning characteristics via varying pump wavelengths, phase matching angle, poling period of PPLT and working temperature. Parametric gain coefficient in the low-loss limit of the THz wave during the DFG process in the vicinity of polariton resonances is numerically analyzed.

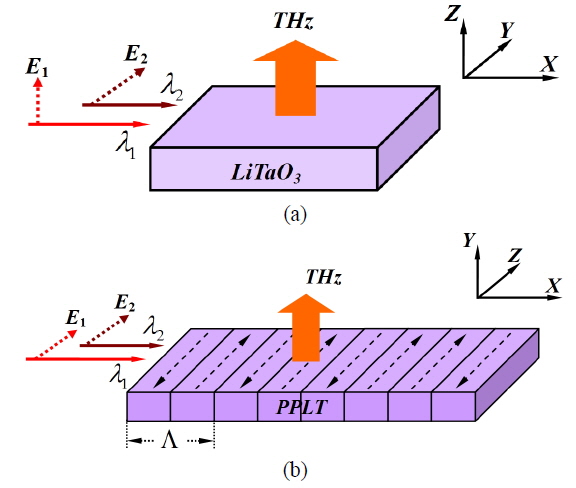
The schematic drawing of surface-emitted DFG in bulk LiTaO₃ and PPLT is presented in Fig. 1. As shown in Fig. 1(a), two input optical waves, λ₁ and λ₂, at the frequencies of ω₁ and ω₂ in the infrared (IR) domain are propagating collinearly along the X axis in a bulk LiTaO₃ crystal and are polarized along the Z and Y axes, respectively. The two optical waves are located close to the lateral surface (XY) of the crystal. A THz wave is emitted due to the oscillating nonlinear polarization at the difference frequency between the two input waves. The radiation angle α between directions of the optical and THz wave propagation is determined by the refractive index of input optical waves in the crystal, and the refractive index of the THz wave,

where K_THz =ω_THzn_THz/c is the wave vector, n_THz is the refractive index at ω_THz frequency; K_IR = n₁^e(θ)ω₁/c - n₂^oω₂/c, n₁^e(θ) and n₂^o are the extraordinary and ordinary refractive indices of optical waves λ₁ and λ₂ at ω₁ and ω₂ frequencies, respectively. θ is the angle between the directions of the optical wave propagation and the optical axis of LiTaO₃. For the THz wave generation based on DFG, the energy conservation condition has to be fulfilled

where λ_THz is the wavelength of the THz wave. From Eq. (1), it follows that the THz wave is emitted perpendicular to the directions of the optical wave propagation if K_IR=0. The effective nonlinear coefficient d_eff in the DFG process is given by

where d₁₅ and d₂₂ are the nonlinear coefficients, the angle φ is an azimuthal angle of the optical wave vector with respect to the X-axis.

As shown in Fig. 1(b), two input optical waves, λ₁ and λ₂, at the frequencies of ω₁ and ω₂ in the infrared (IR) domain are propagating collinearly along the X axis in the PPLT crystal. Both λ₁ and λ₂ are polarized along the Z axis. The two optical waves are located close to the lateral surface (XZ) of the crystal. The optical axis of the LiTaO₃ crystal parallels the Z axis. A THz wave can be generated in a direction perpendicular to the optical wave propagation if poling period Λ of the PPLT satisfies

The parametric gain coefficient g₀ in the low-loss limit during DFG processes in cgs units can be determined by the following expression [16]:

where ω_THz is the absorption coefficient in the THz region, ω_0j, S_j and Γ_j denote eigenfrequency, oscillator strength of the polariton modes and the bandwidth of the jth A₁-symmetry phonon mode in the LiTaO₃ crystal, respectively. I_λ1 is the power density of the optical wave λ₁. d'_E and d'_Q are nonlinear coefficients related to pure parametric (second-order) and Raman (third-order) scattering processes, respectively. In this letter, the data for LiTaO₃ is taken from reference [17].

The theoretical values of the optical wavelengths are calculated using a wavelength- and temperature-independent Sellmeier equation for 0.5% MgO-doped stoichiometric LiTaO₃ (MgO: LiTaO₃)in the IR [18]. The Sellmeier equation for MgO:LiTaO₃ of Dolev et al. [18] in the IR range in a temperature range from room temperature to 200℃ can be written as

where a_1e = 4.5615, a_2e = 0.08488, a_3e= 0.1927, a_4e = 5.5832, a_5e = 8.3067, a_6e = 0.021696, b_1e = 4.782×10⁻⁷, b_2e = 3.0913 ×10⁻⁸, b_3e = 2.7326×10⁻⁸, b_4e = 1.4837×10⁻⁵, b_5e = 1.3647×10⁻⁷, a₁₀ = 4.5082, a₂₀ = 0.084888, a₃₀ = 0.19552, a₄₀ = 1.1570, a₅₀ = 8.2517, a₆₀ = 0.0237, b₁₀ = 2.0704×10⁻⁸, b₂₀ = 1.4449 ×10⁻⁸, b₃₀ = 1.5978×10⁻⁸, b₄₀ = 4.7686×10⁻⁶, b₅₀ = 1.1127×10⁻⁵ and f = (T−24.5)×(T+570.82), T is the crystal temperature in ℃. All the figures in this work were numerically simulated according to the Eqs (1-8) using MATLAB software.

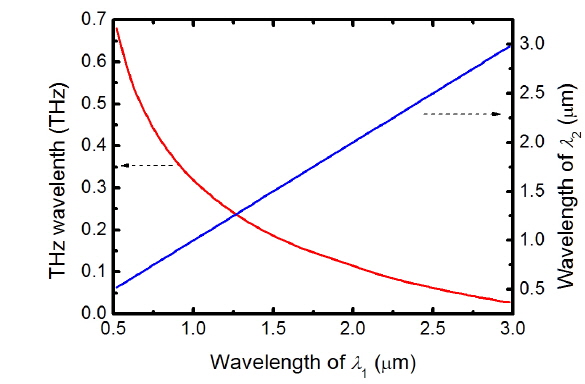
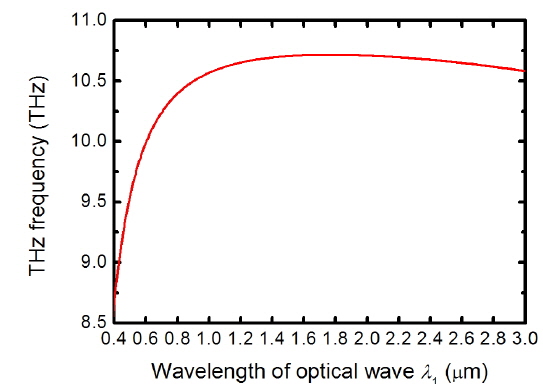
DFG processes are more versatile because of their wide tuning properties. According to Eq. (1-2), the frequencies of the THz wave can be tuned by varying phase-matching angle θ , wavelength of optical waves λ₁ and λ₂ and working temperature T. Figure 2 shows the tuning characteristics versus optical wavelength λ₁. From the figure we find that as λ₁ changes from 0.5 to 3 μm, a THz wave with frequency varying from 0.68 to 0.027 THz can be attained. The frequency of the THz wave is insensitive to the wavelength λ₁ because the refractive index difference between n₁^e(θ) of optical wave λ₁ and n₂^o of optical wave λ₂ changes relatively little with optical wavelength in the infrared range.

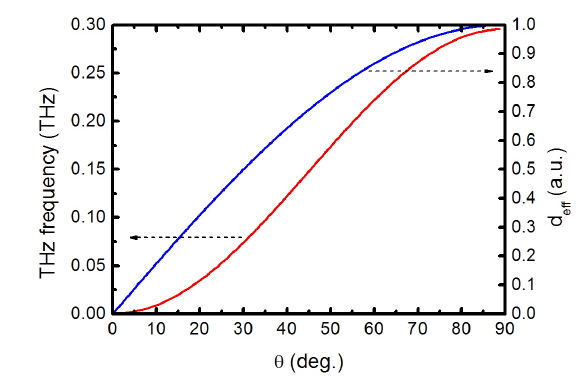
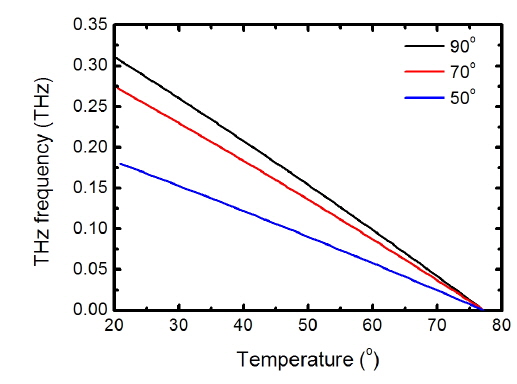
The frequency tuning can be realized by using the dependence of crystal birefringence on angle θ between the directions of the optical wave propagation and optical axis. Figure 3 shows the tuning characteristics versus angle θ . From the figure we find that as θ changes from 0° to 90°, THz wave frequency varying from 0 to 0.3 THz can be attained. The frequency of the THz wave is insensitive to angle θ . As θ changes from 0° to 90°, the effective nonlinear coefficient d_eff gradually increases. When θ equals 90°, the d_eff reaches the maximum value.

Figure 4 shows the tuning characteristics versus working temperature T. As working temperature T varies from 20℃ to 77℃, THz wave frequency changes are relatively small. The tuning range is relatively limited because the difference between n₁^e(θ) of optical wave λ₁ and n₂^o of optical wave λ₂ in the infrared range changes relatively little with working temperature T. According to Eq. (6), with the increase of working temperature T the absorption coefficient α_THz intensively increases due to the increase of the linewidth Γ_j of the A₁-symmetry phonon modes.

According to Eq. (4), the frequencies of the THz wave can be tuned by varying poling period Λ, wavelength of optical wave λ₁ and λ₂, and working temperature T. Figure 5 shows the tuning characteristics versus optical wavelength λ₁ when the poling period Λ equals 13 μm. From the figure we find that as λ₁ changes from 0.4 to 3 μm, frequencies of the THz wave varying from 8.5 to 10.7 THz can be attained. The frequency of the THz wave can be rapidly tuned by varying the wavelength λ₁ when the wavelength λ₁ is less than 1μm. Different from THz wave generation with bulk LiTaO₃ where the frequencies of the generated THz wave are under 1 THz, the frequencies of THz wave generated from PPLT approach the polariton resonances of the LiTaO₃ crystal.

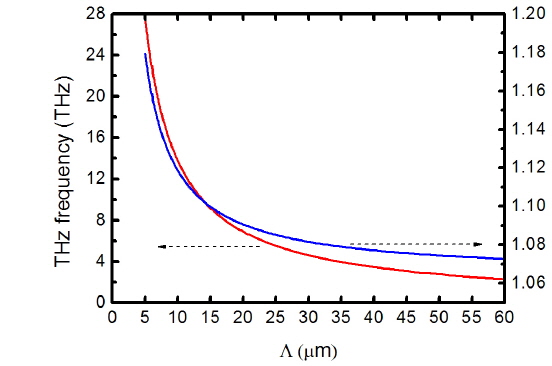
As λ₁ equals to 1.064 μm, the frequencies of THz wave versus the poling period Λ of PPLT are depicted in Fig. 6. From the figure we find that as Λ varies from 5 to 60 μm, a THz wave covering a tuning of 2.3 to 27.6 THz can be realized. The tuning range can cover the entire polariton resonances of the LiTaO₃ crystal. The frequency of THz wave can be rapidly tuned by varying the poling period Λ for Λ less than 20 μm.

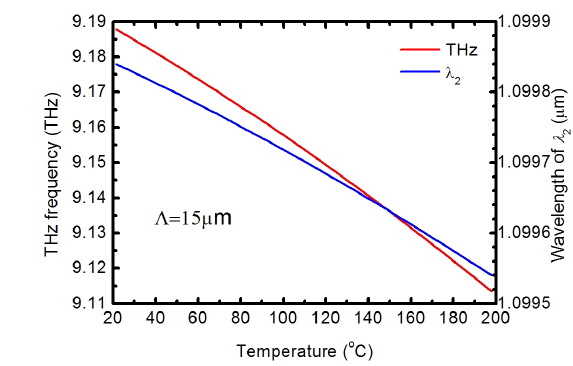
Figure 7 shows the tuning characteristics versus working temperature T. As working temperature T varies from 20℃ to 200℃, THz wave frequency changes relatively little. The rapid tuning of a THz wave cannot be realized by varying working temperature.

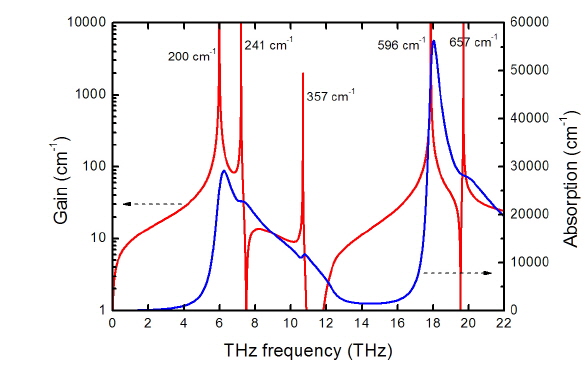
LiTaO₃ crystal has five infrared- and Raman-active transverse optical (TO) phonon modes at the frequencies of 200 cm⁻¹, 241 cm⁻¹, 357 cm⁻¹, 596 cm⁻¹, 657 cm⁻¹, which are called A₁-symmetry modes. The five phonon modes which correspond to the THz wave frequencies of 6 THz, 7.23 THz, 10.71 THz, 17.88 THz and 19.71 THz, are useful for efficient THz wave generation because of the largest parametric gain in the vicinity of phonon polariton resonances, as shown in Fig. 8. From the figure we find that as the THz wave approaches polariton resonances, the parametric gain coefficient g₀ reaches sharply a maximum value and the absorption coefficient α_THz increases intensively to a great value. Such dramatic enhancements of parametric gain coefficients can be exploited for improving the output powers and extending the frequency bands of THz waves if a surface-emitted configuration is employed to minimize the propagation path of the THz wave within the crystal.

Compared with other works in which THz wave generations are far from polariton resonances to avoid intensive absorption, the theoretical model proposed in this letter can exploit dramatic enhancement of parametric gain in the vicinity of polariton resonances with a surface-emitted configuration. The theoretical model proposed in this letter is useful to other materials with crystal birefringence properties, such as LiNbO₃, KTA, in which polaritons are both infrared-active and Raman-active. The theoretical model is also useful to semiconductor optical waveguides with modal birefringence properties. By utilizing modal birefringence of fundamental TE and TM modes in a planar waveguide, the absorption at polariton resonances can be efficiently reduced [19].

THz wave generation at polariton resonance of LiTaO₃ by DFG processes is investigated. It is shown that by using crystal birefringence of bulk LiTaO₃ and grating vector of PPLT, a THz wave can be efficiently generated by DFG in the vicinity of polariton resonances with a Cherenkov phase matching scheme. In the case of bulk LiTaO₃, the frequency of the THz wave is insensitive to the wavelength λ₁, phase matching angle and working temperature. In the case of PPLT, the tuning range of a THz wave is widened by varying the poling period Λ. Dramatic enhancement of parametric gain coefficients in the vicinity of polariton resonances can be exploited for improving the output power and extending the frequency bands of a THz wave by using a surface-emitted configuration to minimize the propagation path of a THz wave within the crystal.