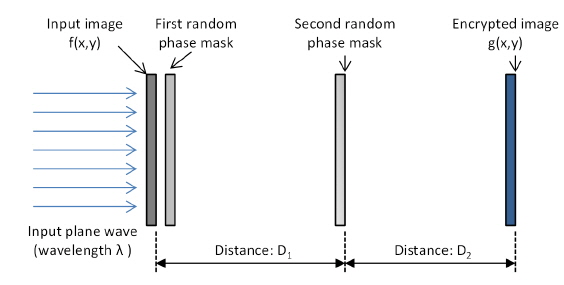
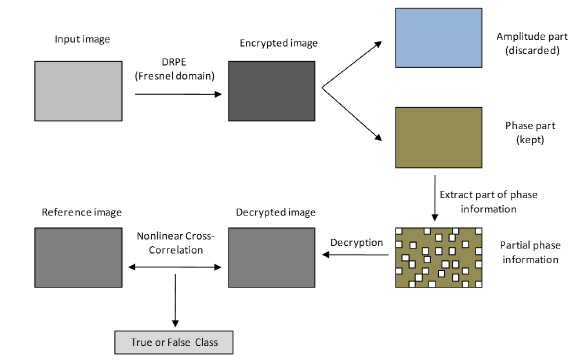
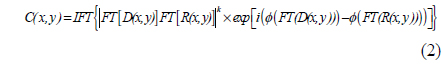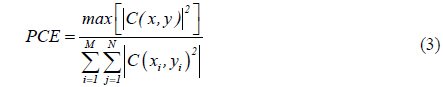The double-random phase encryption (DRPE) algorithm is a robust technique for image encryption, due to its high speed and encoding a primary image to stationary white noise. Recently it was reported that DRPE in the Fresnel domain can achieve a better avalanche effect than that in Fourier domain, which means DRPE in the Fresnel domain is much safer, to some extent. Consequently, a method based on DRPE in the Fresnel domain would be a good choice. In this paper we present an image-authentication method which uses only partial phase information from a double-random-phase-encrypted image in the Fresnel domain. In this method, only part of the phase information of an image encrypted with DRPE in the Fresnel domain needs to be kept, while other information like amplitude values can be eliminated. Then, with the correct phase keys (we do not consider wavelength and distance as keys here) and a nonlinear correlation algorithm, the encrypted image can be authenticated. Experimental results demonstrate that the encrypted images can be successfully authenticated with this partial phase plus nonlinear correlation technique.
Since the double-random phase encryption (DRPE) algorithm was proposed by Refregier and Javidi in 1995 [1], it has been widely used in the fields of image authentication, hiding, encryption, and watermarking [2-17]. This algorithm can be implemented quickly due to its parallel property. Also, the encrypted image from DRPE is stationary white noise, which cannot be predicted by using part of its information. At first the DRPE scheme was only implemented in the Fourier domain, but later algorithms based on DRPE with a Fresnel transform and a fractional Fourier transform were also presented [18-19].
Even though the DRPE technique has achieved good performance in the field of image security, it was also reported that DRPE is not completely robust to chosen-cipher text attacks [20, 21]. To make up for the deficiency of DRPE in the Fourier domain, many new methods were proposed [12-14, 22-26]. In [26], W. Chen and X. Chen used only phase information of an encrypted image resulting from DRPE in the Fourier domain to enhance the security of DRPE. It was also demonstrated that this algorithm is beneficial to data transmission, and can thwart several attack algorithms. In [12, 13], Pérez-Cabré
In [27], I. Moon
This paper is organized as follows: In Section II we describe double-random phase encryption in the Fresnel domain. In Section III we give the procedures for our proposed algorithm, in Section IV we present simulation results based on our method, and we conclude the paper in Section V.
II. DOUBLE-RANDOM PHASE ENCRYPTION
The DRPE encryption technique has been widely used in image security, hiding, and watermarking since it was proposed by Refregier and Javidi [1] in 1995. For DRPE in the Fourier domain [1], the primary image is encoded into a stationary-white-noise image using two random phase masks. All of the points in the stationary-white-noise image are statistically independent and thus cannot be predicted using information from any part of the image. In [18] Situ and Zhang proposed the DRPE method in the Fresnel domain and demonstrated that much higher security is achieved for DRPE in the Fresnel domain than that in the Fourier domain. In [27], I. Moon
For a DRPE system in the Fresnel domain, the input image
where
III. PROCEDURES OF THE PROPOSED AUTHENTICATION METHOD
In our proposed method, the input image is first encrypted with a double-random-phase-encryption technique in the Fresnel domain. Usually the entire encrypted image resulting from DRPE is kept for decryption, the decrypted image being used for further processes such as image authentication and display. However, the encrypted data burden transmission, because all of the encrypted images from DRPE are complex data consisting of amplitude and phase information. Here we discard all of the amplitude data in the encrypted image and keep only the phase information of the encrypted image. To improve the security of the system, only part of the phase information, not all of it, is used. By using partial phase information, the decrypted image is not visually recognizable, which can enhance security [12, 13]. Even though an image decrypted from partial phase information cannot be authenticated visually by comparison to a reference, it is indeed recognized with a nonlinear cross-correlation algorithm. This nonlinear cross correlation is described by the following equation [27, 28].
where
where
One “true class” image and one “false class” image, shown in Fig. 3, are used to illustrate our proposed authentication method. Both are grayscale images of size 250×250 pixels.
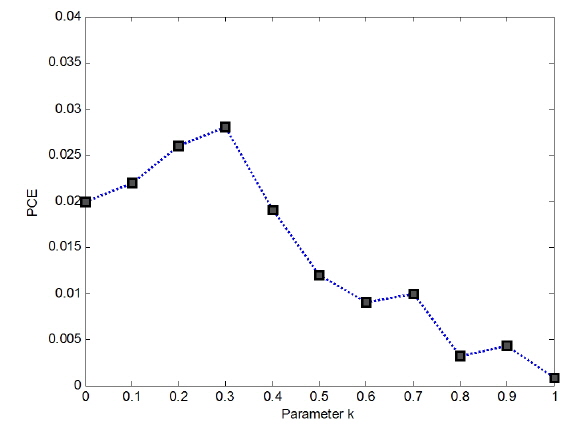
Before conducting image authentication with this proposed algorithm, the parameter
Next the encrypted true class image following DRPE in the Fresnel domain is given in Fig. 5, in which both amplitude and phase information are shown. However, for the image authentication in our proposed algorithm, only part of the phase information is preserved. In this study we randomly choose the phase information that should be kept from the double-random-phase-encrypted image, and a percentage is used to describe the amount of preserved phase information in the encrypted image. A pixel's grayscale value is set to zero for any location with discarded phase information. In Fig. 6 two encrypted images with respectively 20% and 50% phase information preserved are presented.
There is no doubt that the nonlinear cross-correlation values would be different for different preservation fractions of phase information in the original encrypted image. It is necessary to check the minimum percentage of phase information that may be kept while still achieving successful image authentication. Consequently, we varied the percentage of retained phase information in the encrypted image from 9% to 100%, with an interval of 10% (after the value of 10%). In Fig. 7 some of the images decrypted with correct keys in the Fresnel domain are illustrated. Figs. 7(a), (c), (e), and (g) show the true class images decrypted from encrypted images with respectively 20%, 50%, 70%, and 100% preserved phase information. It is noted from these four figures that the silhouette of the decrypted true class images cannot be recognized visually, even when the complete phase information from the encrypted image (see Fig. 7(e)) is preserved, without a priori knowledge of the image. On the contrary, decrypted true class images from encrypted images with both partial amplitude and phase information preserved can be recognized with the naked eye even if only 20% of phase and amplitude information is preserved. Figs. 7(b), (d), (f), and (h) are the decrypted true class images decoded from encrypted images with respectively 20%, 50%, 70%, and 100% phase and amplitude information preserved. The comparisons also show that our proposed image authentication method with only partial phase information preserved in the encrypted image can enhance the security of system, because the decrypted image cannot be easily recognized with the naked eye. Moreover, the encrypted image with partial phase information is beneficial to data transmission, because it requires less bandwidth.
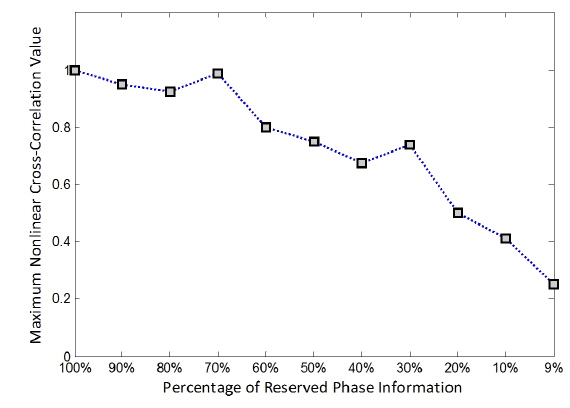
On the other hand, the maximum nonlinear cross-correlation values for true class images are given in Fig. 8. It is noted that the maximum nonlinear cross-correlation values decrease as phase information preserved in the encrypted image decreases. From Fig. 8, it is not easy to visually determine the threshold in terms of percentage that should be preserved from the encrypted image for successful image authentication. Thus it is better to show the maximum nonlinear cross-correlation values using false class images.
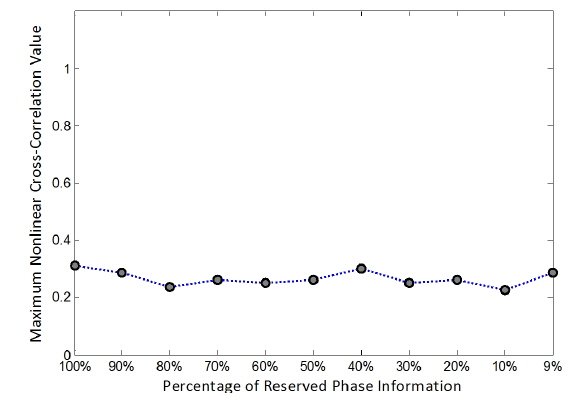
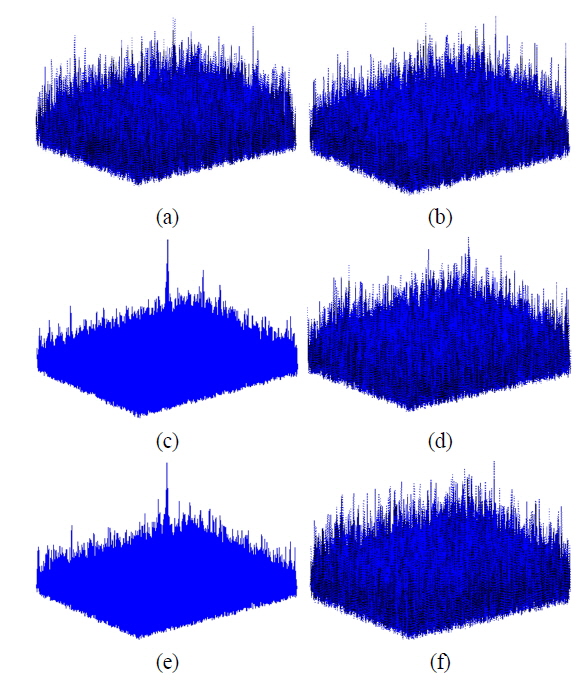
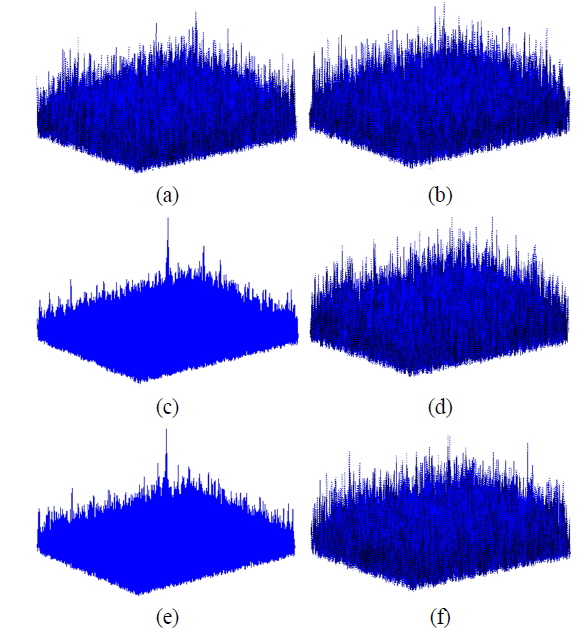
In Fig. 9 the maximum nonlinear cross-correlation values obtained using the same method with a false class image are illustrated. Comparing the results shown in Figs. 8 and Fig. 9, it is found that images can be authenticated when the percentage of preserved phase information is greater than 10%, since the maximum nonlinear cross-correlation values below 10% on the x axis in Fig. 8 are much bigger than the corresponding values in Fig. 9, which means that the true and false class images can be distinguished. However, the true and false class images cannot be distinguished when the preserved phase information in the encrypted image is less than 10%, as the corresponding maximum nonlinear cross-correlation values are very similar. For our system 10% phase information may be the threshold for successful image authentication. In other words, at least 10% of the phase information should be retained in the encrypted image to tell the difference between true and false class images. For a clear illustration concerning the percentage of preserved phase information in an encrypted image, the nonlinear cross-correlation planes are given in Fig. 10 for 9%, 10%, and 20% phase preservation, respectively.
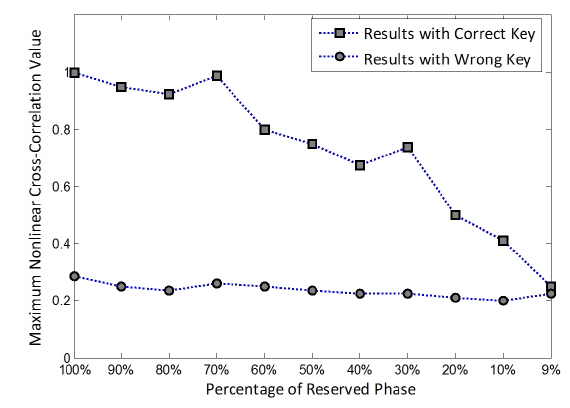
Figure 10 demonstrates that the proposed authentication method can be used to tell true class images from false ones when the percentage of preserved phase information in encrypted images is greater than or equal to 10%. However, an authentication algorithm should satisfy the condition that an image cannot be recognized as true class when an incorrect key is given. In Fig. 11 the maximum nonlinear cross-correlation values between correct and incorrect keys (phase keys) are given for a true class image. It is noted from Fig. 11 that the images cannot be authenticated when the key is wrong, as all of the resulting maximum nonlinear cross-correlation values are very small and similar to those for a false image (see Fig. 9).
In addition, in Fig. 12 the nonlinear cross-correlation planes are given for 9%, 10%, and 20% preserved phases using a true class image, after right and wrong keys have been applied. These results also show that the images cannot be authenticated when the wrong keys for DRPE are used. Moreover, it is seen in Fig. 12 that the percentage of preserved phase information should be at least 10% for successful image authentication.
In this paper we have proposed an image-authentication method based on a double-random-phase-encryption technique in the Fresnel domain. Numerical simulations showed that the decrypted image based on partial phase information in the encrypted image cannot be visually recognized, which can enhance the security of the system. On the other hand, the unrecognizable decrypted image can be authenticated with a nonlinear cross-correlation technique. We have demonstrated the feasibility of this proposed authentication system using both true and false class images. In addition, the image cannot be authenticated if an incorrect key is given. This image-authentication system can achieve superior bandwidth reduction, since only partial phase information from an encrypted image is preserved. Moreover, it is shown that a true class image can be successfully authenticated even when only a small percentage of phase information from the encrypted image is preserved.