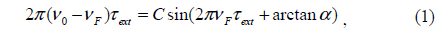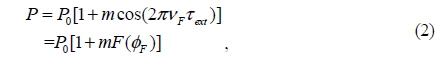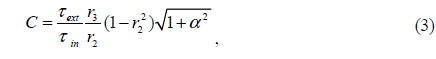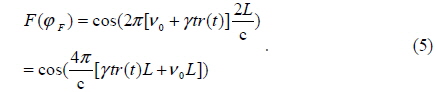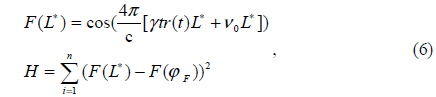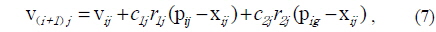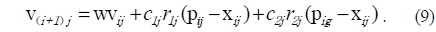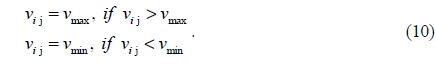Laser ranging techniques are widely used for both industrial and scientific application in contactless measurement as nondestructive testing, in contrast to other measuring technologies that have to contact the target surface [1]. Laser ranging techniques have the potential to improve the productivity of manufacturers and the quality of manufactured products due to their swiftness and high precision.

Heretofore, conventional optical distance measurement methods can technically be put into three categories: interferometry, time-of-flight and triangulation methods [2]. It is undeniable that these traditional methods can exhibit high accuracy, but the applications are limited due to their short unambiguity range determined by the wavelength used [3] or to their complicated experimental setups. Thus, these methods are inappropriate when the measurement is carried out in a narrow space. For example, in consideration of their dimensions, there is not enough space to install devices based on conventional methods for cylinders with inner diameters of less than 10 centimeters.

Fortunately, this shortcoming can be overcome by a very interesting coherent technique called self-mixing interferometry (SMI) [4]. The SMI system is simpler than conventional interferometers because many optical elements, such as the beam splitter, reference mirror, and external photodetector, are not required [5]. The self-mixing phenomenon occurs when the laser beam is partially reflected by a target in an external cavity and mixed with the light inside the laser cavity, which results in variation in emitted power and lasing frequency [6]. Information about the motion of the target can be deduced by an integrated phototransistor through analyzing the variation.

The inquiry into distance measurement based on SMI has attracted much attention during the past few decades due to its simplicity, compactness, and low cost [7]. Many methods have been presented which use the linear relation between beat frequency and distance [8-13], such as counting the number of mode hops [8] or utilizing the interpolated FFT [13]. Most signal-processing work has focused on spectrum estimation algorithms until recently, and resultant measurement resolution has been promoted to 0.1 mm [13]. However, in terms of signal-processing theory, inherent drawbacks of the spectrum estimation algorithms such as spectrum leakage will influence the measurement of beat frequency and degrade the accuracy of distance measurement. Moreover, further post processing such as adjustment is often required to extract the accurate frequency [14], which makes the measurement complex.

In order to avoid the shortcomings of spectrum estimation algorithms, we propose the use of optimization algorithms to estimate the distance information, which eschews spectrum estimation and searches for the minimum of a fitness function. The fitness function is established based on the SMI signal that contains the distance information. The function is a multimodal function and obtains the sole global minimum that corresponds to the actual distance. Because of this, we can estimate distance by means of searching for this global minimum.

Traditional optimization methods such as Newton’s method and some intelligence algorithms such as the genetic algorithm (GA) [15] and the PSO algorithm [16] can extract absolute distance from the self-mixing signal. Newton’s method is widely used among local searching algorithms due to its fast convergence ability. This method can be utilized if we initialize a certain number of points searching local optima simultaneously in the predicted area, and then find the minimum of all local optimal solutions, thus preventing trapping into local optima. However, the performance of this method depends largely on initialization of points and searching step size, which are difficult to adjust in practical measurements. What is more, the elapsed time of Newton’s method is higher than other optimization methods due to the large number of points. As to intelligence algorithms, we take GA and PSO under consideration, as they have versatility and ability to optimize various kinds of multimodal functions. However, the process of coding should be implemented before calculation, and there are some other complex operations in the genetic algorithm during the calculation, such as crossover and mutation. More parameters should be taken into consideration in comparison with PSO. As a result, we choose PSO to estimate the distance.

The paper is organized as follows: Section II presents the detailed theoretical analysis about self-mixing interferometry and the particle swarm optimization algorithm. Experimental results and comparison with interpolated FFT are discussed in Section III. In Section IV, the influence of different external feedback strength parameter C and an optimal selection of inertia weights are presented. Conclusions are drawn in Section V.

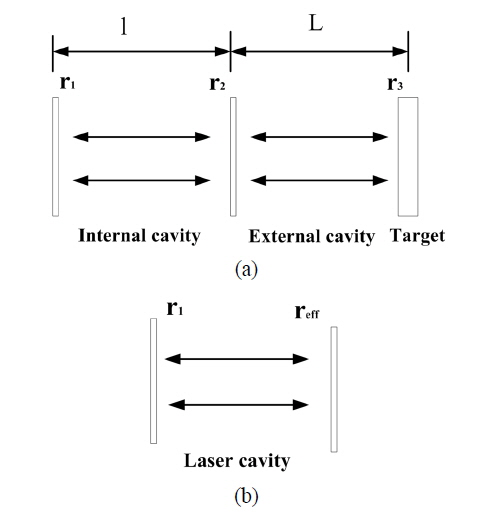
A schematic arrangement for a solitary single-mode laser diode (LD) under external feedback can be represented by a three-facet Fabry-Perot cavity and simplified by a two-facet Fabry-Perot cavity, as shown in Fig. 1.

Here r₁ and r₂ are the amplitude reflection coefficients of the LD facets, r₃ is the amplitude reflectivity of the external target, l is the length of the laser cavity and L is the length of the external cavity. Neglecting the multiple reflections within the external cavity and for weak feedback level when the reflection coefficient r₃ of the target is far less than r₂, the frequency of the equivalent cavity and the emitted optical power P can be expressed as:

ν₀ and ν_F are the optical frequency of LD without feedback and under optical feedback, respectively, P₀ is the optical power without light feedback, α is the linewidth enhancement factor, and m is the modulation coefficient. τ_ext is the roundtrip time of the light beam in the external cavity [8]. The external feedback strength parameter C is defined by

here τ_in denotes the roundtrip time in the laser internal cavity. The parameter C is an important parameter affecting the dynamics of LD as well as its output power. Weak feedback level (C<1) gives a single solution of ν in Eq. (1) and makes ν_F approximate ν₀ [17]. We will discuss the influence of this parameter in Section 4.1.

When the sawtooth current is injected into the laser, ν_F can be expressed as

here γ means the relation between lasing frequency and modulation current with a unit Hz/mA. F(φ_F) can be expressed as：

The distance L is contained in F(φ_F) and we can estimate this information by PSO. For the purpose of application, a fitness function H is established as Eq. (6).

L^* is the estimated distance and F(L^* ) is the established function with the variable L^* , n is the number of sampling points of the SMI signal. L^* is the approximate absolute distance when the fitness function H obtains the minimum. A simulation in the range from 10 to 16 cm with the actual distance 13 cm was performed and the function is proved to be a multimodal function owning only one global minimum. The actual distance is obtained when the fitness function reaches the minimum as shown in Fig. 2.

The particle swarm optimization is a parallel evolutionary computation technique based on the social behavior metaphor. The PSO algorithm is initialized with a population of random candidate solutions in a predicted area, conceptualized as particles [18]. Each particle is treated as a point to represent an estimated distance and the particles are updated at each iteration. The ith iteration of particles can be represented as X_i=(x_i1,x_i2,…,x_in), and n is the number of particles. The best previous position that gives the best fitness value of each particle is recorded and represented as P_i=(p_i1,p_i2,…p_in). The best particle among all the particles is denoted by P_ig. Each particle is assigned a randomized velocity which adds to its position in order to change its previous position iteratively. The velocity is represented as V_i=(v_i1,v_i2,…v_in). [19]

The velocity of each particle is updated according to its current position. The difference between the best position of each particle and the individual’s current position is stochastically added to the current velocity, causing the trajectory to oscillate around the best position of each particle. Simultaneously, the difference between the best position of all particles and the individual’s current position is also stochastically added to the current velocity. Thus, the particle is adjusted to search around the two best positions and all particles get close to global best position [20]. With a sufficient number of iterations, the global best position approximates the actual distance where the fitness function obtains the minimum.

In summary, the jth particle (j=1,2,…n) is updated with the following equations [21]

here c_1j and c_2j are two positive constants called the cognitive and social parameters, respectively. r_1j and r_2j are two random functions in the range [0,1].

The first part of the Eq. (7) is the previous velocity of the particle. The second part represents the private thinking of the particle itself and the third part represents the collaboration among the particles [22]. Thus the new velocity of each particle can be calculated with the contribution of its previous velocity and the distances of its current position from its own best experience (position) and the group’s best experience. Eq. (7) exhibits local search ability without the first part and more likely global search ability by adding the first part. In order to balance the two abilities, an inertia factor w is brought into the Eq. (7) as shown in Eq. (9) [23].

The factor w plays the role of balancing the global search and local search. It can be a positive constant or even a positive linear or nonlinear function of time. The selection of this factor is discussed in Section 4.2.

In addition, the velocities of the particles are confined within [v_min, v_max] as in Eq. (10) to guarantee that the particles are confined to searching in forecasted space [24].

PSO has the ability to search global minima working on a population of potential solutions. However, this algorithm has the drawback of time complexity. In practical measurements, the actual distance is unknown and we have to estimate the range of measurement. Because of this, there is large amount of calculation with searching into such a wide range.

In order to decrease the time consumed, we implemented a way to shrink the exploration range [15] before the implement of PSO to accelerate the speed of measurement. During the accelerating, the range of all points will be updated according to the performance of the last iteration of particles. The maximum and the minimum of a fraction of particles ranked in the front to get the best fitness function value will be selected to establish the new range. The particles that give the maximum and the minimum should also be added to the next iteration to avoid the neglect of the actual distance. Because of this, the range will be shrunk to a small range around the actual distance after several iterations of update. After the accelerating, the PSO can find out the global minima within several tens of iterations, which can significantly decrease the time consumed.

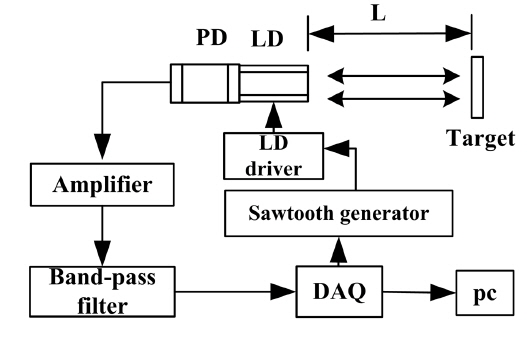
We implemented some experiments to confirm the validity of the PSO algorithm, and the experimental setup is exhibited in Fig. 3.

The VCSEL HVS6003-001 with an integrated phototransistor and a threshold current of 2 mA was utilized in the experiment. It emits a polarized beam with a central wavelength of 850 nm. The VCSEL is driven by a modulated sawtooth current with amplitude 1 mA and frequency 50 Hz, biased at 7 mA. The current is generated by a digital to analogue output channel of NI’s DAQ card.

SMI signal occurs when the laser beam is partially reflected by the diffusive target and mixed with the light inside the laser cavity. The SMI signal can be detected by the built-in phototransistor and transformed into light current and then into voltage signal by a sampling resistance. The voltage signal is digitized and sampled by a DAQ card with sampling rate of 100 kHz after the process of an amplifier and a band-pass filter. A PC running the PSO algorithm was utilized to process the samples. The parameters of the algorithm are exhibited as follows. A recommended choice for constant c₁ and c₂ is integer 2 since it on average makes the weights for “social” and “cognition” parts to be 1 [16]. The population size is 60; the maximum number of iterations is 20; the maximum velocity is set as 0.002; inertia weight w is 0.4. Each particle is initialized in the range from 1 cm to 25 cm, which can be forecasted before the implementation of the algorithm. During the accelerating, 15 particles ranked in the front to get the best fitness function value are selected to establish the new range, and accelerating iteration is set to 5.

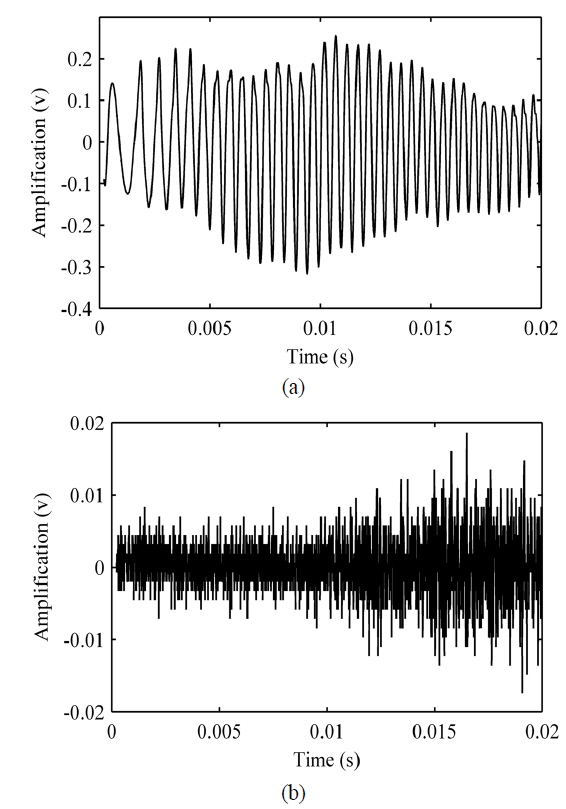
The SMI signal during a modulation period is shown in Fig. 4 (a), the corresponding noise without feedback is shown in Fig. 4 (b). The sinusoidal waveform in Fig. 4 (a) shows that the device works under weak feedback regime (C<1) [25]. After calculating the effective value, we can obtain the SNR of experimental data, which is about 30 dB.

The target is fixed on a mechanical translator with precision 3 µm. A series of absolute distance measurements was made to acquire the resolution of the algorithm. The target was moved 1 cm a step in the range from 3 cm to 20 cm. The error and STD values evaluated from 30 samples by PSO are presented in Fig. 5 (a). To compare the performance of PSO with interpolated FFT based on spectrum estimation algorithm, we utilized the interpolated FFT to process the same experimental data. The error and STD values are presented in Fig. 5 (b).

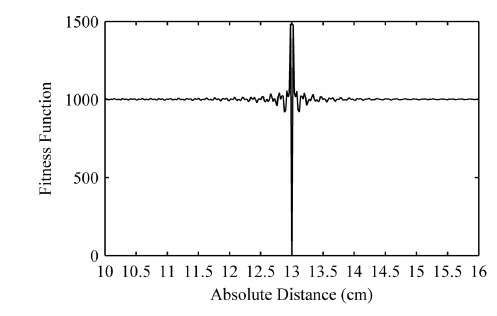
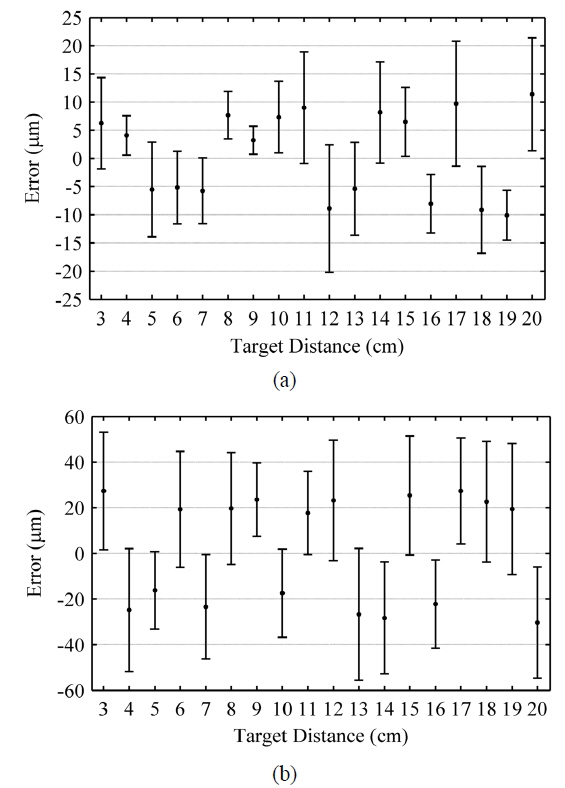
A resolution better than 25 μm in the range from 3 to 20 cm can be seen from Fig. 5 (a) to demonstrate the performance of PSO in processing of the SMI signal. In addition, the results from Fig. 5 illustrate that the PSO algorithm has superiority to interpolated FFT in resolution and stability. This result may be explained by the following reasons. Interpolated FFT suffers from inherent drawbacks such as spectrum leakage, which will influence the measurement of beat frequency and degrade the accuracy of distance measurement. What is more, inapplicability in the condition with dense frequency spectrum will further worsen the measurement. Whereas, the PSO depends on the fitness function that is established from the self-mixing signal. For this matter, PSO is appropriate to realize high resolution and stability in the absolute distance estimation eschewing the difficulty in frequency analysis.

However, PSO performs well at the expense of being time consuming. We processed the same data in MATLAB environment on the PC with dual-core 2.8 GHz CPU and 2 GB RAM. The elapsed time of PSO is nearly 10 s while the elapsed time of interpolated FFT is less than 1 s due to the fast calculation algorithm. Because of the application of accelerating, the elapsed time of PSO has decreased from more than 80 s to nearly 10 s at the same resolution level. Further optimization should be investigated to accelerate the calculation. For example, a simpler fitness function will reduce the amount of calculations, and high seed devices such as FPGA have the potential ability to decrease the time consumed.

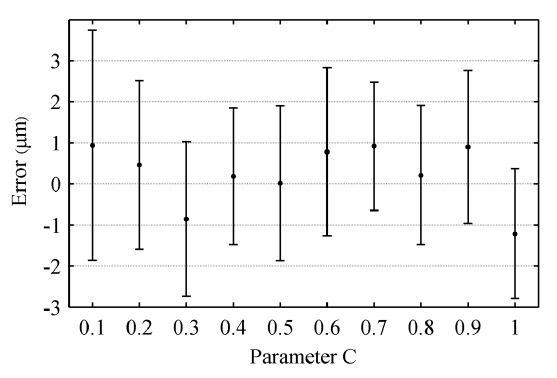
A single solution for v in Eq. (1) is obtained in the case of weak feedback level corresponding to C less than 1, and the waveform shows that our experiment was conducted under this condition. The change of feedback strength parameter influences the SMI signal which contains the information of distance, and may influence the accuracy of measurement. It is necessary to assess the extent of the effect. However, the parameter C cannot be adjusted freely and quantitatively in experiment, some simulations on MATLAB were performed. Theoretical calculation of function F(φ_F) for different parameters is presented in Fig. 6.

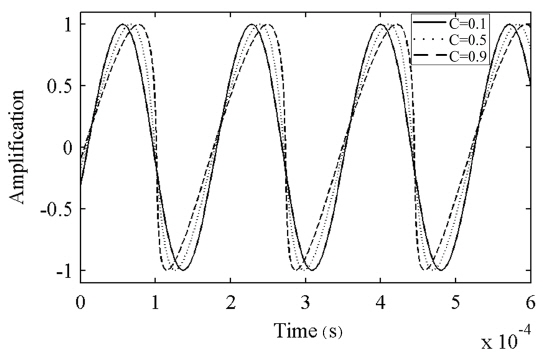
For a very weak optical feedback level when C is equal to 0.1, the function F(φ_F) is nearly sinusoidal. With the increase of C, F(φ_F) exhibits a slight distortion. In order to evaluate the influence which the parameter C has on the PSO performance, some simulations were performed. The simulations deploy the same parameters as in the experiment. The parameter C changes linearly from 0.1 to 0.9 at a distance of 5 cm and the corresponding simulation error and STD values on the condition of SNR 30 dB are shown in Fig. 7.

As we can see from Fig. 7, the change of parameter C in the weak feedback level has little influence on the results. In light of this, there is not much reason to regulate this parameter when the setup works in the case of weak feedback. The simulation results are better than experimental results in Fig. 5, as there are other sources of error that limit the resolution of this device. Firstly, a variation to the beat frequency occurs, since optical frequency is not strictly linear to the current modulation [26]. As a result, the resolution of distance measurement is limited. To improve the accuracy of our device, a reshaped modulation current may be needed to suppress the nonlinearity. Secondly, measurement resolution can also be affected by the fluctuations in temperature which may lead to instability of the laser frequency. The SMI signal will deviate from the ideal waveform and then the deviation can degrade the accuracy of the result. A temperature controller should be added to adjust the stability of temperature.

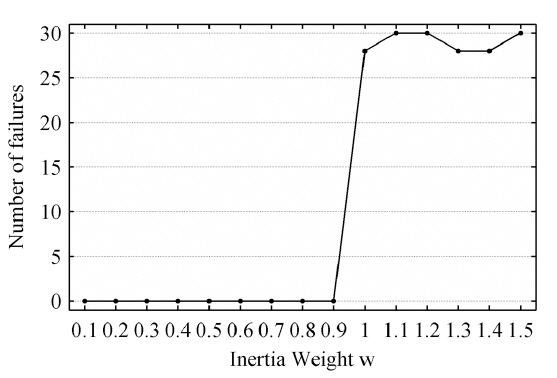
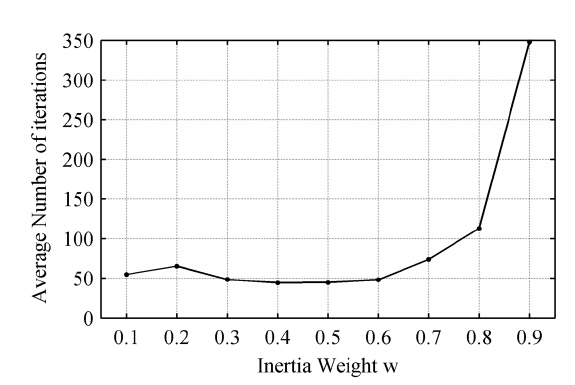
The inertia weight w is important to balance global search ability and local search ability. A larger inertia weight tends to facilitate global exploration while a smaller one tends to facilitate local exploration. There is a tradeoff between the global and local search which requires fewer iterations on average to find the optimum [20]. Some simulations on MATLAB were performed to select the optimal parameter. These simulations were conducted without accelerating to eliminate the stochastic influence of it. The maximum number of iterations is 2000 and the parameter w changes from 0.1 to 1.5 at a distance of 5 cm. For each selected w, thirty runs are performed and the required iterations for finding the acceptable solution with an error less than 1μm are recorded. If the algorithm cannot find the acceptable solution within 2000 iterations, it is claimed that the algorithm fails to find the global optimum in this run. The number of failures versus inertia weights is shown in Fig. 8. It is easy to see most runs fail to find the acceptable solution when w is greater than 1, and the others perform well. The average number of iterations versus inertia weights when w is less than 1 is presented in Fig. 9.

It is observed that there is no distinct difference in the number of iterations when w is less than 1 and the minimum occurs when w is equal to 0.4, thus we adopted this value in the experiment. The inertia weight also can be a positive linear or nonlinear function of time [27]. Further research has to be carried out to find the optimal function and suitable range of inertia weight.

In this paper, an approach of SMI based on particle swarm optimization for absolute distance estimation is proposed. The PSO algorithm with an inertia weight was utilized to find the optimal solution of the multimodal fitness function and then to estimate the actual distance value. Some experiments were implemented to demonstrate the validity of this algorithm and the superiority to interpolated FFT in process of SMI signal, and the absolute distance was estimated with a resolution superior to 25 μm in the range from 3 to 20 centimeters. Some simulations with different external feedback strength parameter C were performed and the results show there is little difference on the condition of weak optical feedback level. An inertia weight (w=0.4) was adopted in the algorithm after the comparison of the number of iterations acquired to find the acceptable solution. Further investigation about simpler fitness functions and application of high speed devices is necessary to decrease the time consumed. Also, future analysis about nonlinearity in optical frequency with current tuning and parameters selection in the algorithm have the potential ability to improve the accuracy of SMI distance estimation.