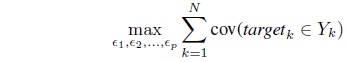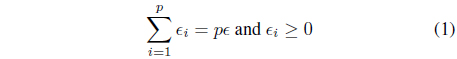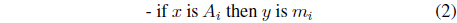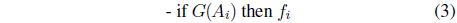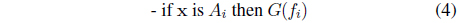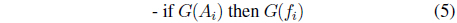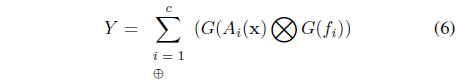It is apparent that there are no ideal models. Numerical data are not ideally captured (i.e., captured without any error) by any model, irrespective of the model’s complexity. Informed by the principle of Ockahm’s razor, we strive to build simple models and establish a balance between the requirements of accuracy and simplicity. In spite of the diversity of the architecture of models (especially those emerging in the realm of computational intelligence), many challenges remain. An interesting, innovative, and promising direction is to conceptualize and build models at a higher level of abstraction; in this manner, the models become capable of better coping with the system to be modeled. These models can be constructed in terms of information granules; in what follows, these are referred to as granular models. Information granules are formalized in various settings such as sets (intervals), fuzzy sets, and rough sets. Depending on the nature of the model, we can talk about granular neural networks, granular regression models, etc.

The objective of this study is to conceptualize information granularity as an essential design asset in system modeling, which, when used properly, can make the model match the complexity of the problem (system) and gives rise to a hierarchy of granular models (models of type-1, type-2, etc.) to cope with the complexity of the system under discussion.

The remainder of this paper is organized as follows. To make the material self-contained, we start with a brief summary of granular computing (Section 2). In Sections 3 and 4, we develop a characterization of information granules, discussing their two important characterizations, namely, coverage abilities (related to the generalization facet of information granules) and specificity description. We also identify their complementary nature, which must be dealt with at the modeling level. The concept of granular models is studied in Section 5; here, we consider the idea of creating granular parameters of the original numeric model, demonstrating how they give rise to granular results. The detailed protocols for determining the granular parameters of the models are covered in Section 6. Then, a detailed example of rule-based architectures is considered to demonstrate how the parameters of the model are realized in the form of information granules (Section 7). Section 8 is devoted to the realization of the hierarchy of granular models, resulting in type-2 granular models and (in general) type-n granular models. Conclusions are presented in Section 9.

To provide a better idea of this study and to make it self-contained, we present a concise introduction to granular computing, which is a formal conceptual framework for data analysis and modeling tasks.

Information granules are intuitively appealing constructs that play a pivotal role in human cognition and decision-making. We perceive complex phenomena by reconciling existing knowledge with available experimental evidence and structuring them in the form of meaningful, semantically sound entities; these entities are central to all ensuing processes for describing the world, reasoning about the environment, and supporting decision-making. The term information granularity has emerged in different contexts and has numerous areas of application, and therefore, carries various meanings. In artificial intelligence, information granularity is central to problem solving through problem decomposition, in which various subtasks are formed and solved individually. In general, an information granule is a collection of elements drawn together by their closeness (resemblance, proximity, functionality, etc.), articulated in terms of some useful spatial, temporal, or functional relationship. Granular computing considers representing, constructing, and processing such information granules.

We can refer here to some areas that offer compelling evidence as to the nature of underlying processing and interpretation in which information granules play a pivotal role:

image processing, processing and interpretation of time series, granulation of time, and design of software systems. Information granules are abstractions. As such, they naturally give rise to hierarchical structures: the same problem or system can be examined at different levels of specificity (detail) depending on the complexity of the problem, available computing resources, and particular goals to be addressed. The hierarchy of information granules is inherently visible when processing information granules. The level of detail (which is represented by the size of information granules) becomes an essential part of the hierarchical processing of information, where different levels of the hierarchy are indexed by the size of information granules.

Even the commonly encountered simple examples presented above indicate that (a) information granules are a key component of knowledge representation and processing; (b) the level of granularity of information granules (their size) becomes crucial to the problem description and the overall problem-solving strategy; (c) the hierarchy of information granules is an important aspect of the perception of phenomena and offers a tangible method of dealing with complexity, namely, by focusing on the most essential facets of the problem; and (d) there is no universal level of granularity for information; essentially, the size of granules becomes problem-oriented and user-dependent.

There are several well-known formal settings in which information granules can be defined and processed.

Sets (intervals) realize a concept of abstraction by introducing the notion of a dichotomy: an element belongs to a given information granule or not. In addition to set theory, we have the well-developed discipline of interval analysis. Alternatively to an enumeration of elements belonging to a given set, sets are described by characteristic functions taking on values in {0, 1}.

Fuzzy sets [16, 17] provide an important conceptual and algorithmic generalization of sets. By allowing partial membership of an element in a given information granule, we increase realism. This phenomenon helps in cases in which the principle of dichotomy is neither justified nor advantageous. The description of a fuzzy set is given in terms of membership functions taking on values in the unit interval. Formally, a fuzzy set A is described by a membership function mapping the elements of a universe X to the unit interval [0, 1].

Shadowed sets [10] offer an interesting description of information granules by distinguishing among elements that either fully belong to the concept, are excluded from it, or whose belongingness is unknown. Formally, these information granules are described by the mapping X : X → {1, 0, [0, 1]}, where the elements with a membership quantified as the entire [0, 1] interval are used to describe the shadow of the construct. Given the nature of the mapping here, shadowed sets can be considered a granular description of fuzzy sets, where the shadow is used to determine unknown membership values, which, in fuzzy sets, are distributed over the entire universe of discourse. Note that the shadow produces non-numeric descriptors of membership grades.

Probability-oriented information granules are expressed in the form of probability density functions or (simple) probability functions; they capture a collection of elements resulting from an experiment. Based on the concept of probability, the granularity of information becomes a manifestation of the occurrence of different elements. For instance, each element in a set has a probability density function truncated to [0,1], which quantifies the degree of membership to the information granule.

Rough sets emphasize the roughness of the description of a given concept X when realized in terms of the indiscernibility relation that is provided in advance. The roughness of the description of X is given by its lower and upper approximations of a certain rough set. One can refer to a plethora of applications.

From the perspective of this study, there are two important and directly applicable characterizations of information granules, namely coverage and specificity [9-11].

Coverage The concept of coverage of information granule, cov(.) is discussed with regard to some experimental data existing in Rⁿ, that is {x₁, x₂, . . . , x_N} and as the name stipulates, is concerned with its ability to represent (cover) these data. In general, the larger number of data is being “covered”, the higher the coverage measure. Formally, the coverage is a non-decreasing function of the number of data that are represented by the given information granule A. Depending upon the nature of information granule, the definition of cov(A) can be properly expressed. For instance, when dealing with a multidimensional interval (hypercube) A, cov(A) in its normalized form is related with the cardinality of the data belonging to A, . For fuzzy sets the coverage is realized as a s-count of A, where we summed up the degrees of membership of x_k to A, .

Specificity Intuitively, the specificity relates to a level of abstraction conveyed by the information granules. The higher the specificity, the lower the level of abstraction. The monotonicity property holds: if for the two information granules A and B one has

A ⊂ B (when the inclusion relationship is articulated according to the formalism in which A and B are expressed) then specificity, sp(.) [14] satisfies the following inequality: sp(A) ≥ sp(B). Furthermore for a degenerated information granule comprising a single element x₀ we have a boundary condition sp({x₀})= 1. In case of a one-dimensional interval information granules, one can contemplate expressing specificity on a basis of the length of the interval, say sp(A)= exp(−length(A)); obviously the boundary condition specified above holds here. If the range range of the data is available (it could be easily determined), say, then sp(A)= 1 − |b − a|range where A = [a, b], range= [min_k x_k, max_k x_k].

The realizations of the definitions can be augmented by some parameters that contributes to their flexibility. It is also intuitively apparent that these two characteristics are associated: the increase in one of then implies a decrease in another: an information granule that “covers” a lot of data cannot be overly specific and vice versa.

By information granules of higher type (2 ^nd type and n^th type, in general) we mean granules in the description of whose we use information granules rather than numeric entities. For instance, in case of type-2 fuzzy sets we are concerned with information granules- fuzzy sets whose membership functions are granular. As a result, we can talk about interval-valued fuzzy sets, fuzzy fuzzy sets (or fuzzy² sets, for brief), probabilistic sets and alike. The grade of belongingness are then intervals in [0,1], fuzzy sets with support in [0, 1], probability functions truncated to [0,1[, etc. In case of type -2 intervals we have intervals whose bounds are not numbers but information granules and as such can be expressed in the form of intervals themselves, fuzzy sets, rough sets or probability density functions. Information granules of higher order are those whose description is realized over a universe of discourse whose elements are information granules. In some sense rough sets could be sought as information granules of order-2. Information granules have been encountered in numerous studies reported in the literature; in particular stemming from the area of fuzzy clustering [4][12] in which fuzzy clusters of type-2 have been investigated [5] or they are used to better characterize a structure in the data and could be based upon the existing clusters [13].

The concept of the granular models form a generalization of numeric models no matter what their architecture and a way of their construction are. In this sense, the conceptualization offered here are of general nature. They also hold for any formalism of information granules. A numeric model M₀ constructed on a basis of a collection of training data (x_k, target_k), x_k ∈Rⁿ and target_k∈R comes with a collection of its parameters a_opt where a∈R^p. Quite commonly, the estimation of the parameters is realized by minimizing a certain performance index Q (say, a sum of squared error between target_k and M₀(x_k)), namely a_opt= arg Min_a Q(a). To compensate for inevitable errors of the model (as the values of the index Q are never equal identically to zero), we make the parameters of the model information granules, resulting in a vector of information granules A = [A₁ A₂. . . A_p] built around original numeric values of the parameters a. The elements of the vector a are generalized, the model becomes granular and subsequently the results produced by them are information granules. Formally speaking, we have

- granulation of parameters of the model A = G(a) where G stands for the mechanisms of forming information granules, viz. building an information granule around the numeric parameter - result of the granular model for any x producing the corresponding information granule Y, Y= M1(x, A) = G(M0(x))= M0(x, G(a)).

Information granulation is regarded as an essential design asset. By making the results of the model granular (and more abstract in this manner), we realize a better alignment of G(M₀) with the data. Intuitively, we envision that the output of the granular model “covers” the corresponding target. Formally, let cov(target, Y) denote a certain coverage predicate (either Boolean or multivalued) quantifying an extent to which target is included (covered) in Y.

The design asset is supplied in the form of a certain allowable level of information granularity e which is a certain non-negative parameter being provided in advance. We allocate (distribute) the design asset across the parameters of the model so that the coverage measure is maximized while the overall level of information granularity serves as a constraint to be satisfied when allocating information granularity across the model, namely . The constraint-based optimization problem reads as follows

subject to

The solution to the problem can be produced by invoking one of the protocols outlined in Section 6.

The monotonicity property of the coverage measure is apparent: the higher the values of e, the higher the resulting coverage. Hence the coverage is a non-decreasing function of e.

Along with the coverage criterion, one can also consider the specificity of the produced information granules. It is a non-increasing function of e. The more general form of the optimization problem can be established by engaging the two criteria leading to the two-objective optimization problem

- determine optimal allocation of information granularity [ϵ1, ϵ2, . . . , ϵp]so that the coverage and specificity criteria become maximized.

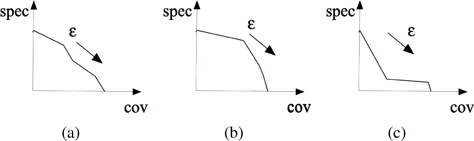
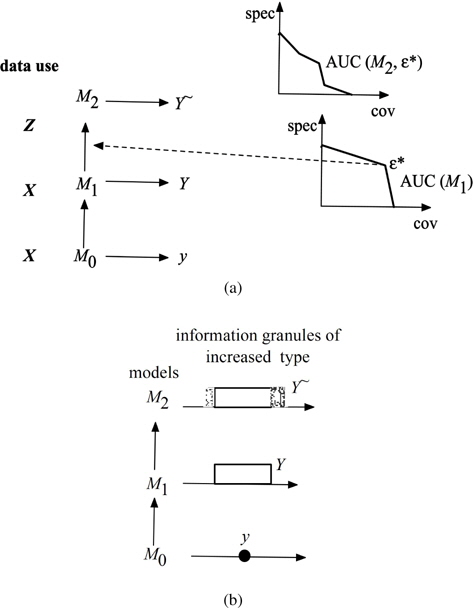
Plotting these two characteristics in the coverage –specificity coordinates offers a useful visual display of the nature of the granular model and possible behavior of the behavior of the granular model as well as the original model. Several illustrative plots shown in Figure 1 illustrate typical changes in the specificity/coverage when changing the values of information granularity e. One can consider those coming as a result of the maximization of coverage while reporting also the obtained values of the specificity. There are different patterns of the changes between coverage and specificity. The curve may exhibit a monotonic change with regard to the changes in e and could be approximated by some linear function. There might be some regions of some slow changes of the specificity with the increase of coverage with some points at which there is a substantial drop of the specificity values. A careful inspection of these characteristics helps determine a suitable value of e – any further increase beyond this limit might not be beneficial as no significant gain of coverage is observed however the drop in the specificity compromises the quality of the granular model. Furthermore Figure 1 highlights an identification of suitable values of the level of information granularity. The global behavior of the granular model can be assessed in a global fashion by computing an area under curve (AUC) of the coverage-specificity curve present in Figure 1. Obviously, the higher the AUC value, the better the granular model. The AUC value can be treated as an indicator of the global performance of the original numeric model produced when assessing granular constructs built on their basis. For instance, the quality of the original numeric models M₀ and M′₀ could differ quite marginally but the corresponding values of their AUC could vary quite substantially by telling apart the models. For instance, two neural networks of quite similar topology may exhibit similar performance however when forming their granular generalizations, those could differ quite substantially in terms of the resulting values of the AUC.

As to the allocation of information granularity, the maximized coverage can be realized with regard to various alternatives as far as the data are concerned: (a) the use of the same training data as originally used in the construction of the model, (b) use the testing data, and (c) usage of some auxiliary data.

The numeric parameters of the model are to be made granular. In what follows, to illustrate the idea, we consider interval information granules spanned over the numeric values. The allocation of information granularity can be realized in many different ways by engaging various levels of sophistication. The series of protocols presented below is organized with the increasing level of flexibility each of them supporting a better usage of information granularity:

P₁: uniform allocation of information granularity. This protocol is the simplest one. It does not invoke any optimization mechanism. All numeric values of the parameters are treated in the same way and become replaced by intervals of the same length. Furthermore the intervals are distributed symmetrically around the original values of the parameters.

P₂: uniform allocation of information granularity with asymmetric position of intervals around the numeric parameter. Here we encounter some level of flexibility: even though the intervals are of the same length, their asymmetric localization brings a certain level of flexibility, which could be taken advantage of during the optimization process. More specifically, we allocate the intervals of lengths ϵ_γ and ϵ(1 − γ) to the left and to the right from the numeric parameter where γ ∈ [0, 1] controls asymmetry of localization of the interval whose overall length is e. Another variant of the method increases an available level of flexibility by allowing for different asymmetric localizations of the intervals that can vary from one parameter to another. Instead of a single parameter of asymmetry (γ) we admit individual γ_i for various numeric parameters.

P₃: non-uniform allocation of information granularity with symmetrically distributed intervals of information granules. Each parameter of the model is endowed with the individual level of information granularity ϵ_i.

P₄: non-uniform allocation of information granularity with asymmetrically distributed intervals of information granules. Among all the protocols discussed so far, this one exhibits the highest level of flexibility.

P₅: An interesting point of reference, which is helpful in assessing a relative performance of the above methods, is to consider a random allocation of granularity. By doing this, one can quantify how the optimized and carefully thought out process of granularity allocation is superior over a purely random allocation process.

While the allocation of information granularity realized above through a collection of protocols offers several main strategies, some of the implementation details are dependent on the nature of the model. For instance if all parameters of the model are in the same range, say [0,1] (as encountered in fuzzy neural networks operating logic operators) then the intervals around the numeric parameter a_i are formed as shown above, namely

P₁ [a_i − ϵ/2, a_i + ϵ/2]

P₂ [a_i − ϵγ, a_i + ϵ(1 − γ)] or [a_i − ϵγ□, a_i + ϵ(1 − γ□)]

P₃ [a_i − ϵ/2, a_i + ϵ□/2]

In case the parameters of the model are localized in different ranges, the realization of the intervals involves the magnitude of the parameters, say for P₁

[a_i(1−ϵ/2), a_i(1+ϵ/2)] if a_i ≠ 0 and [a_i − ϵ/2, a_i+ϵ/2] if a_i ≠ 0

These functional rules (Takagi-Sugeno format of the conditional statements) link any input space with the corresponding local model whose relevance is confided to the region of the input space determined by the fuzzy set standing in the input space (A_i). The local character of the conclusion makes an overall development of the fuzzy model well justified: we fully adhere to the modular modeling of complex relationships. The local models (conclusions) could vary in their diversity; in particular local models in the form of constant functions (m_i) are of interest

These models are then equivalent to those produced by the Mamdani-like rules with a weighted scheme of decoding (defuzzification). There hs been a plethora of design approaches to the construction of rule-based models, cf. [1-3, 6-8, 18, 19].

Information granularity emerges in fuzzy models in several ways by being present in the condition parts of the rules, their conclusion parts and both. In a concise way, we can describe this in the following way (below the symbol G(.) underlines the granular expansion of the fuzzy set construct abstracted from their detailed numeric realization or a granular expansion of the numeric mapping).

(i) Information granularity associated with the conditions of the rules. We consider the rules coming in the format

where G(A_i) is the information granule forming the condition part of the i-th rule. An example of the rule coming in this format is the one where the condition is described in terms of a certain interval-valued fuzzy set or type-2 fuzzy set, G(A_i).

(ii) Information granularity associated with the conclusion part of the rules. Here the rules take on the following form

with G(f_i) being the granular local function. The numeric mapping f_i is made more abstract by admitting granular parameters. For instance instead of mi we consider G(m_i) where G(m_i) is an interval or a linear function whose parameters are fuzzy numbers.

(iii) Information granularity associated with the condition and conclusion parts of the rules. This forms a general version of the granular model and subsumes the two situations listed above. The rules read now as follows

The augmented expression for the computations of the output of the model generalizes the expression used in the description of the fuzzy models (3). We have

where the algebraic operations shown in circles ⨂ and ⊕ reflect that the arguments are information granules instead of numbers (say, fuzzy numbers). The detailed calculations depend upon the formalism of information granules being considered. Let us stress that Y is an information granule. Obviously, the aggregation given by (6) applies to (i) and (ii) as well; here we have some simplifications of the above stated formula. The two commonly used formalisms already reported in the literature are interval-valued fuzzy sets and type 2 fuzzy sets [15].

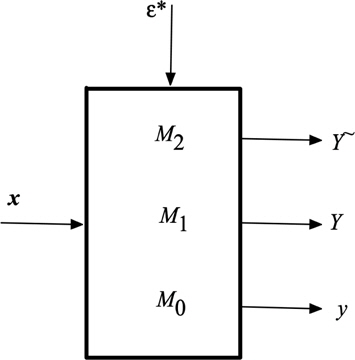
The construction of the granular model can be expanded to form additional layer of the granular constructs and granular models. In essence, we develop a models whose granular parameters are made information granules of higher type, say those of type-2.

We proceed with a construction of the granular model of type-2 by forming their granular parameters on a basis of the initially available parameters of the numeric model M₀. Let us recall that the granular parameters A₁, A₂, . . . , A_p have been formed on a basis of the data X. Considering a certain value of the level of information granularity e (whose selection was made on a basis of the analysis of the coverage –specificity characteristics, refer to Figure 2) has been selected, say e₀, there are still some data remaining that are not “covered” by this granular model. Denote by Z these residual data not covered by the granular model produced at the first level of the hierarchy. They can be referred to as type-1 (granular) outliers. Now the parameters A_i are made information granules of higher type with anticipation that this could help cover the data present in Z. In brief, we form an information granule of type-2 . The construction of is completed in such a way so that the data in X are “covered” by the model with type-2 information granules. Here one can envision a certain tradeoff between coverage and specificity offered by different values of e. The hierarchy of the models is visualized in Figure 2. Here we highlight a way in which the granular parameters are built and an emergence of the construct of higher type.

Proceeding with the specific realization of information granules, in case of interval-valued parameters, we observe an emergence of the visible hierarchy of information granules of higher type (granular intervals). Originally, the model M₀ produces numeric results (sought of information granules of type-0). The model formed at the next layer of the hierarchy (M₁) generates intervals Y whereas moving to the next layer of the hierarchy (model M₂) the results are in the form of granular intervals (whose bounds are apparently information granules themselves). The nature of the results is visualized in Figure 2 (a).

In parallel, we show a series of hierarchically structured models, Figure 2 (b) where the successive layers of the model are invoked depending upon the predefined levels of information granularity e and e*. For any input x they produce a numeric output, granular output (Y) and granular output of type-2 Y^~. The formation of the granular model of type-2 is implied by the predefined level of e*. Again the detailed design of the parameters of the models in the form of type-2 information granules is realized in the similar way as discussed in case of granular parameters (resulting in type-1 granular models). We allocate information granularity to the bounds of the intervals of A₁, A₂, . . . , A_p so that the coverage of data X is maximized. As before one can monitor the behavior of the granular model formed in this way by inspecting the values of coverage and specificity.

There are two boundary situations worth emphasizing:

(a) selecting the values of e* for which the highest coverage is attained. In this situation, we are left with a small set of data Z to be dealt with at the next level of the hierarchy, in particular Z could be empty

(b) selecting e* such that the highest specificity is attained. Now the data to be processed by M₂ is almost the same as X, Z≈X.

One could solve a certain optimization problem formulated as follows. We choose such ϵ∗ for which AUC(M₂, ϵ∗) attains its maximal value, viz. ϵ∗_opt = arg Max AUC(M₂, ϵ∗). This makes the type-2 granular model optimized with regard to the level of information granules specified at the lower conceptual level.

If the information granules are realized as fuzzy sets, following this scheme, we produce type-2 or interval –valued fuzzy sets of results, see Figure 3. Again as before, in the optimal allocation of information granularity we engage methods of evolutionary optimization in the realization of the protocols outlined in Section 6.

The above construction can carried out at the higher levels of hierarchy leading to granular models of type-3, 4, etc. In this case the successive data being used in the resulting constructions could be sought as outliers of type-1, type-2, etc.

With regard to the hierarchy outlined above, we may draw a certain analogy with some well known linear regression models. It is obvious that in the models of this class, for any x one easily determines the numeric output (y) or augment it in the form of the confidence interval – this corresponds to the two levels of the above hierarchy where the models M₀ and M₁ have been established.

This study proposed a new direction for granular modeling of constructs of higher types. Successive granular system modeling can lead to the formation of granular parameters of type-1, type-2, etc. and to the production of models of type M₁, M₂, . . . , M_n. The containment relationship holds in the design of the series of models; starting from M₀, they are developed to enhance the functionality of the successively constructed models by engaging information granules of higher types. Along with the realization of the models, one can also identify potential outliers, which, depending on the level of modeling at which they arise, can be labeled type-0, type-1, or type-2 (granular) outliers. The increasing number of types of information granules is beneficial; however, one must be aware that unless there are some legitimate reasons not to, confining the system to type-2 information granules (and related models) is a sound choice.