A submerged body moving near the free surface needs to maintain its attitude and position to accomplish missions. It is necessary to validate the performance of a designed controller before a sea trial. The hydrodynamic coefficients of maneuvering are generally obtained by experiments or computational fluid dynamics, but these coefficients have uncertainty. Environmental loads such as the wave exciting force and suction force act on the submerged body when it moves near the free surface. Thus, a controller for the submerged body should be robust to parameter uncertainty and environmental loads. In this paper, the six-degree-of-freedom equations of motions for the submerged body are constructed. The suction force is calculated using the double Rankine body method. An adaptive control method based on an artificial neural network and proportional-integral-derivative control are used for the depth controller. Simulations are performed under various depth and speed conditions, and the results show the effectiveness of the designed controller.
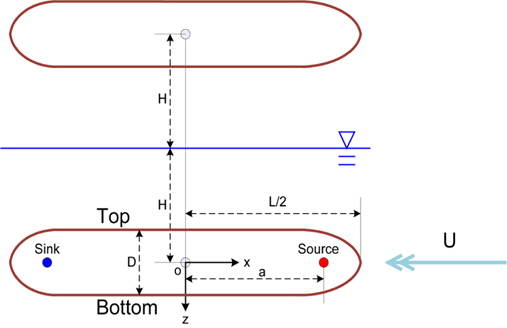
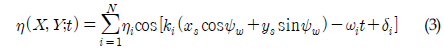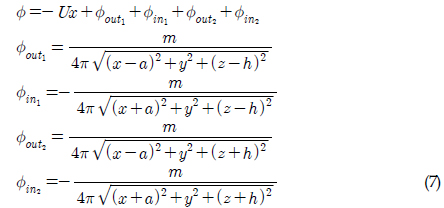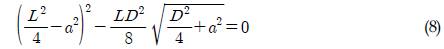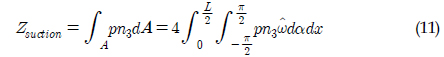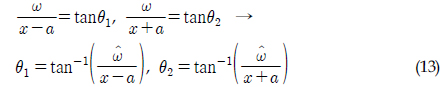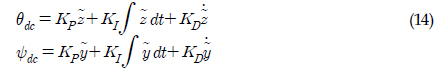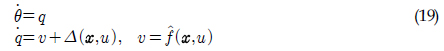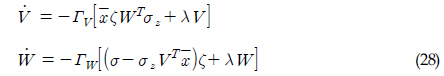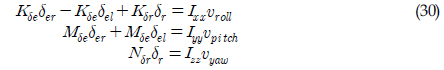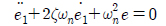몰수체는 주로 깊은 수중에서 운항하지만 임무에 따라 수면 근처에서 운항하는 경우가 있다. 잠수함의 경우 수상표적을 탐색하거나 잠망경 심도에서 운항을 하게 되며, 디젤 잠수함의 경우 축전지의 충전을 위해 주기적으로 스노클 항해를 한다. 무인잠수정은 Global positioning system (GPS) 신호를 수신하거나 외부와 통신을 할 필요가 있는 경우 수면 근처에서 운항을 한다. 수면근처에서 운항하는 경우 몰수체에 작용할 수 있는 환경하중으로는 파랑력, 수면과의 간섭효과로 인한 흡인력, 조류력이 있다. 이러한 환경하중하에서 몰수체가 심도를 유지하며 임무를 수행하기 위해서는 자세 및 심도 제어기 설계가 필요하고 설계된 제어기의 효과를 해상시험 전에 시뮬레이션을 통하여 검증해 보는 작업은 필수적이다.
시뮬레이션에 사용되는 동역학 모델링은 주로 모형시험이나 전산유체역학을 통하여 수행되는데 이러한 방식에는 모델링 오차를 수반하게 된다. 따라서 몰수체의 수면근처 심도제어를 위해 모델링의 오차 및 환경하중과 같은 외란에 강건한 제어기법을 통한 제어기 설계가 요구된다.
몰수체에 대한 운동방정식 구성과 유체력 미계수를 확보하기 위한 연구는 1960년대부터 활발히 연구되었다. Gertler and Hagen(1967)은 몰수체에 작용하는 유체동역학적 힘을 여러 개의 비선형계수들의 조합으로 분해하여 몰수체의 6자유도 운동방정식을 제안하였다. Feldman(1979)은 급격한 운동시에 몰수체 길이에 걸쳐 다르게 작용하는 비선형힘 및 연성힘을 선체길이에 따라 적분하여 구하는 방법을 통하여 급격한 운동 시 증가하는 비선형 효과를 잘 반영할 수 있는 운동방정식을 구성하였다. Dumlu and Istefanopulos(1995)는 잠수함의 보조탱크를 고려한 운동방정식을 정립하였으며, 확률론적인 이론을 도입한 제어기를 설계하였다. Prestero(2001)는 REMUS AUV의 시뮬레이터를 개발하기 위하여 구속모형 실험 및 자유항주를 통한 유체력 미계수 확보하였고 이를 기반으로 제어기를 설계하였다. 수면근처에서 운항하는 몰수체의 심도 제어에 관한 연구는 proportional-integral-derivative (PID), Linear quadratic regulator (LQR), Fuzzy 등을 이용한 제어기 설계가 주를 이루었다(Richards and Stoten, 1982; Hao et al., 2004; Choi et al., 2006; Choi et al., 2008; Kim et al., 2009; Shao et al., 2012). Hao et al.(2004)는 Fuzzy 이론을 이용하여 잠수함의 파 중 제어기를 설계하였다. Choi et al.(2006)과 Choi et al.(2008)는 3차원 패널 방법을 이용하여 불규칙 파 중에서의 파 강제력 수학 모형을 제안하고 PID 제어기법을 이용하여 잠수함의 심도 유지 시뮬레이션을 수행하였다. Kim et al.(2009)은 몰수체의 심도 제어에 있어 PID 제어의 한계를 분석한 후 LQR 제어기법을 이용하여 연직면 운동 시스템의 제어를 수행하였다. Shao et al.(2012)는 Richards and Stoten(1982)의 운동방정식을 토대로 실린더 형상의 소형 몰수체에 대한 심도제어기를 설계하였다. 위에서 언급한 수면근처에서 운항하는 몰수체의 심도 제어에 관한 연구들의 한계는 다음과 같다. 첫째로 선행 연구들은 3자유도 연직 운동만을 고려하여 제어기를 설계하였기 때문에 6자유도 운동을 하는 실제 몰수체의 운동에 적용하기 어려울 수 있다는 점이다. 특히 횡파로 인해 횡동요가 일어나는 경우 물체고정좌표계 기준 상하방향이 지구고정좌표계 기준 상하방향과 일치하지 않기 때문에 횡동요 제어를 하지 않으면 심도의 오차가 커질 수 있다. 두 번째로 수면 근처 운항에서 몰수체에 작용할 수 있는 흡인력을 고려하여 제어기 설계를 한 연구가 없다는 점이다. 흡인력에 대한 모델링 연구는 수행된 바 있지만(Yoon and Trung, 2009) 이를 고려하여 몰수체의 심도 제어기 설계를 수행한 연구는 문헌에 보고된 바 없다. 세 번째로 선행연구에서 사용한 제어기법이 모델링 불확실성에 강건하지 않은 점이다. 선행 연구에서 사용된 PID-LQR-fuzzy와 같은 제어기는 일정 운항조건에서는 효과적일 수 있으나 다양한 운용 조건에서도 좋은 성능을 발휘한다고 보장할 수 없다.
선행연구들의 단점을 보완하기 위하여 본 연구에서는 조류는 없다고 가정하고, 파랑력과 흡인력을 고려하여 수면근처에서 운항하는 몰수체의 심도 제어기를 설계하였다. International towing tank conference (ITTC)에서 제시한 파랑 스펙트럼으로 규칙파의 파 진폭을 도출하고 선형 이론을 통하여 불규칙파를 구현하였고 계산된 파 강제력을 시뮬레이션에 적용하였다. 흡인력의 경우, Rankine 물체를 수면을 기준으로 상하에 위치시킨 후 아래 Rankine 물체에 작용하는 수직방향 압력을 적분하여 계산하였다. 이 결과를 여러 속도와 심도에 대해 미리 계산한 뒤 곡선 맞춤하여 시뮬레이션의 흡인력으로 고려하였다. 조종운동을 모사하기 위하여 6자유도 운동방정식을 사용하였고 횡동요-종동요-선수동요 방향 제어기를 설계하였다. 제어기는 외부루프와 내부루프로 구성하였다. 외부루프 제어기는 위치를 피드백하여 몰수체가 추종해야 할 자세를 출력해주고 내부루프에서는 외부루프에서 출력된 자세를 추종할 수 있도록 하였다. 외부루프는 PID 제어기법을 사용하였으며 몰수체의 동역학과 관련된 내부루프는 불확실성에 강건하도록 인공신경망을 이용한 적응제어기법을 통하여 제어기를 설계하였다. 설계된 제어기의 성능을 검증하기 위하여 여러 가지 운항 속도와 심도에 대하여 제어 시뮬레이션을 수행하였다.
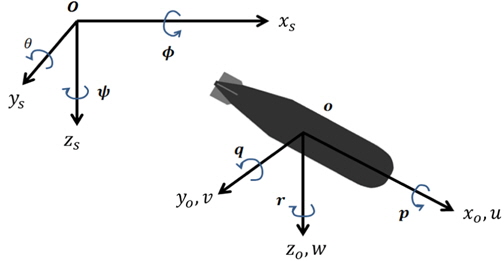
운동 방정식을 구성하기 위하여 지구고정좌표계와 물체고정 좌표계를 설정하였다. 지구고정좌표계
본 연구의 대상은 길이 대 직경비가 12.17이고 상하 및 좌우 대칭형인 몰수체이다. 선수 제어판은 없으며 선미에 십자형으로 된 제어판을 장착하고 있다. 대상 몰수체의 경우 침로변경시 편류각이 적고 직진성이 좋은 특성을 갖고 있기 때문에 선형 운동방정식으로 동적 특성을 표현할 수 있다. 대상 몰수체의 6자유도 선형 운동방정식은 식 (1)과 같이 표현할 수 있다.
여기서
파랑력을 구하기 위하여 우선 불규칙파를 구현하였다. 불규칙파는 다음의 ITTC에서 제시한 Bretschneider 형태의 스펙트럼으로 다음과 같이 표현한다.
파랑 스펙트럼이 주어지면 이것을 구분하여 선형 이론을 이용하여 규칙파의 합으로 불규칙파를 재현한다.
파랑력의 경우 선형이론에 의하여 방사력, 산란파, Froude-Krylov힘의 중첩으로 표현할 수 있다. Sea state 4에서 모달 주기는 8.8초이고 분산관계식에 의하여 파장은 120.9m인데 대상 몰수체의 길이는 파장에 비하여 매우 작아서 산란력 및 방사력은 무시 가능하다고 가정하였다. 이번 연구에서는 Froude-Krylov에 의한 파 강제력을 Newman(1977)을 참고하여 1차항만 고려하였고 유도된 식을 정리하면 식 (4)와 같다.
여기서 ∇는 배수용적,
여기서, 은 이고 는 지구고정좌표계에서 물체고정좌표계로의 오일러 좌표변환 행렬이다. Froude- Krylov힘에 의한 모멘트는 식 (6)과 같이 물체고정좌표계에 대하여 기술된 Froude-Krylov 힘 벡터에 의하여 나타낼 수 있다. 여기서,
계산된 파 강제력은 선형운동방정식 (1)의 우변에 더해져 시뮬레이션에 고려된다.
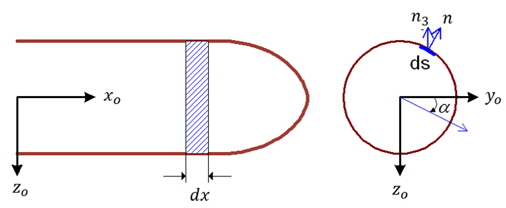
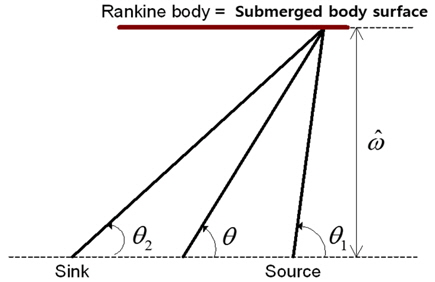
몰수체가 수면근처에서 항주하면 몰수체를 중심으로 상하의 유동이 비대칭이 되어 수직방향으로 힘이 작용하는데 이를 흡인력으로 정의한다. 몰수체에 작용하는 흡인력은 Rankine 물체를 수면을 기준으로 상하에 위치시킨 후, 아래 Rankine 물체에 작용하는 수직방향 압력을 적분하여 구하였다.
이중 Rankine 물체의 속도 포텐셜은 수면을 기준으로 상하부에 소스, 싱크(Streeter, 1948)를 배치하면 된다. 여기서, 하부 소스는
여기서,
몰수체의 길이
Rankine 물체 표면에서의 압력은 Bernoulli 방정식에 의하여 다음과 같이 유동 속도를 이용하여 나타낼 수 있다.
여기서,
위식에서 을 알기 위해서는
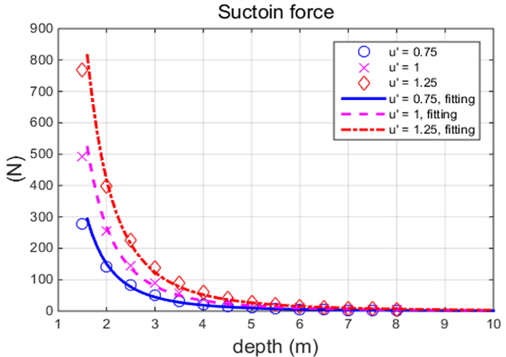
소스의 위치를 구할 때와 마찬가지로 Newton 방법으로 를 구하였다. 소스의 위치, Rankine 물체의 높이를 정하는데 시행 착오법(Iteration)을 사용하므로 실제 시뮬레이션 프로그램에 위의 계산식을 그대로 적용하는 데는 문제가 있다. 따라서 속도 및 심도별로 사전에 계산을 해놓고 계산값을 곡선 맞춤하여 시뮬레이션에 적용하였다. 흡인력 계산은 수심범위 1.5~8.0m, 전진방향 속도를 기준속도로 무차원화 시킨
계산 결과 속도가 빠를수록 그리고 수면 근처에 있을수록 흡인력이 몰수체에 크게 작용하는 것을 알 수 있다. 계산된 흡인력은 지구고정좌표계 기준이므로 몰수체가 수면 근처를 항주하는 중에 횡동요가 발생한 경우에는 회전변환을 이용하여 흡인력을 물체고정좌표계로 변환시켜 준다.
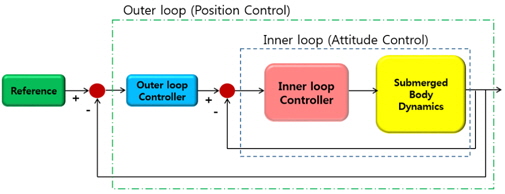
대상 몰수체의 경우 선수 제어판이 없고 선미 제어판만 있기 때문에 자세의 변화 없이 위치를 제어하는 것은 불가능 하다. 따라서 종동요 각과 선수동요 각의 변화를 통하여 심도 및 좌우방향 위치를 제어하는 것이 현실적이다. 본 연구에서는 제어 알고리즘을 이중루프로 구성하였다. 외부루프 제어기는 위치의 오차를 피드백하여 몰수체가 추종해야 할 오일러 각을 출력해준다. 내부루프 제어기는 외부루프 제어기의 출력된 오일러 각과 몰수체가 추종하기 위한 제어력을 계산한다. 원하는 위치에 도달할 수 있도록 오일러 각을 출력해 주는 외부루프는 몰수체의 동역학과 관련이 없기 때문에 제어이득 조정이 용이한 PID를 사용하였다. 내부루프는 몰수체의 동역학과 관련이 있기 때문에 모델링 불확실성에 강건한 제어기법인 인공신경망을 사용하여 제어기를 설계하였다. 설계된 제어 알고리즘을 블록선도로 표현하면 Fig. 7과 같다.
외부루프 제어기는 PID 제어기법을 이용하여 설계하였다. 심도는 종동요 각을 이용하여 제어하고 좌우방향 변위는 선수동요 각을 이용하여 제어한다. 외부루프에서 출력되는 명령 종동요 각 및 명령 선수동요 각을 수식으로 표현하면 식 (14)와 같다.
여기서, , 는 각각 심도 오차와 좌우변위 오차로서 , 와 같이 표현할 수 있다. 내부루프 제어기 설계부분에서 설명하겠지만, 내부루프 제어기 부분에서는 명령 종동요 각과 명령 선수동요 각 뿐만 아니라 명령 종동요 각속도와 각가속도 그리고 명령 선수동요 각속도와 각가속도가 필요하다. 각속도와 각가속도를 매 시간마다 출력되는 명령 각과 Time step을 가지고 미분하여 구하면 수중운동체에 장착된 센서 노이즈에 의해서 원치 않는 값이 출력 될 수도 있고 심지어 각속도와 각가속도의 부호가 바뀌는 상황이 발생할 수도 있다. 따라서 외부루프의 기준모델을 도입해서 내부루프의 입력값이 되는 기준각, 기준 각속도, 기준 각가속도를 출력하도록 하였다. 외부루프 기준모델을 식 (15)와 같이 2차 선형 시스템으로 설정하였다.
식 (15)의 2차 선형 시스템의 해를 수치적으로 구하여 내부루프의 입력값인 를 도출한다. 횡동요는 항상 0이 되어야 하므로 으로 설정하였다.
내부루프 제어기의 경우 몰수체의 자세를 제어한다. 시뮬레이션에 사용되는 몰수체의 동역학은 모델링 오차를 포함한다. 오차를 포함하는 모델링을 바탕으로 제어기를 설계하면 실제 몰수체의 운용에서는 불안정한 운동이 야기될 수 있기 때문에 모델링 오차에 강건한 적응제어기법을 이용하여 내부루프 제어기를 설계하였다. 인공신경망을 이용한 적응제어 기법은 몰수체 동역학을 모델링 된 항과 모델링 되지 않은 항으로 분리하고 모델링된 항을 역변환을 통하여 피드백 선형화 한다. 적응제어법칙을 통해 모델링 되지 않은 항을 추정하여 보상하고 남은 항을 PD제어기법을 통하여 제어한다. 종동요-횡동요-선수동요 각 모두 인공신경망을 통하여 제어기를 설계하였다. 인공신경망 적응제어기 설계과정의 예로 종동요 각 제어기 설계 방법을 기술하였다. 종동요 운동방정식은 다음과 같이 일반적인 비선형 함수로 표현할 수 있다.
여기서,
비선형 시스템에서 모델링이 되지 못한 부분을 모델링의 불확실성으로 간주할 수 있으며, 이 부분 역시 상태와 제어입력의 함수이다. 식 (17)에서 비선형함수
식 (18)에서 모델링이 된 부분 을 의사제어
만약 정확한 모델링이 가능하다면 시스템이 선형화되므로, 일반적인 선형제어기법을 적용할 수 있다. 의사제어
식 (21)과 같이 추종오차를 정의하고, 선형제어기로써 PD제어기를 선택하여 추종오차 방정식을 구성하면 식 (22)와 같다.
위의 식 (22)에서 오차들을 하나의 상태벡터로 두고 전체 식을 행렬형태로 표현하면 다음과 같다.
여기서, , ,
식 (23)에서 제어게인
종동요 운동방정식에서 어느 부분까지를 모델링할 것인지는 설계자의 선택이며, 정확하지 않은 모델링은 제어 성능에 악영향을 미칠 수 있다. 간단한 설계를 위해 식 (25)와 같이 승강타에 관련된 항만을 모델링된 부분으로 설정하였다.
모델링 불확실성을 보상할 수 있는 인공신경망 적응제어기의 구조 및 설계과정에 대해 기술한다. 인공신경망은 구조를 전혀 알 수 없는 함수를 주어진 입력변수들을 이용하여 근사하는 역할을 한다. 본 논문에서는 Single hidden layer를 사용하였다. 구조를 알 수 없는 모델링 불확실성이 어떤 변수들의 함수가 될지를 고려하여 적절한 상태변수들을 입력변수로 결정하여야 한다. 결정된 상태변수들에 입력 Bias항
인공신경망 뉴런의 개수와 각 뉴런에 대응되는 Activation potential의 값은 설계자에 의해 결정된다. 인공신경망 뉴런의 개수가 많아질수록 더 정확한 근사화가 이루어지지만, 계산시간이 증가하므로 적절한 개수의 선택이 중요하다. 본 논문에서는 시뮬레이션을 결과를 이용하여 뉴런의 개수를 6개로 구성하였고 Activation potential 값들을 결정하여 주었다. 마지막으로 Hidden layer를 거친 변수들이 출력가중변수
입력가중변수
여기서,
위의 업데이트 식은
정리하자면 인공신경망에서의 출력값은 적응제어신호
내부루프에서 계산된 의사제어를 승강타와 타에 할당시켜 줘야 한다. 이는 수식 (24)에 표현되어 있는 의사제어의 역변환에 해당한다. 승강타와 타에 의한 모멘트와 제어력 간의 관계식을 통하여 제어판 각을 결정한다. 의사제어와 제어판 각의 관계식은 식 (30)과 같이 표현할 수 있다.
여기서
대상 몰수체의 제어판 각의 한계는 20deg로 설정하였고 제어판 회전 각속도의 한계는 100deg/s로 설정하였다.
제어이득을 결정하기 위하여 우선 내부루프의 제어기의 이득을 결정한다. 내부루프의 PD제어이득인
감쇠비
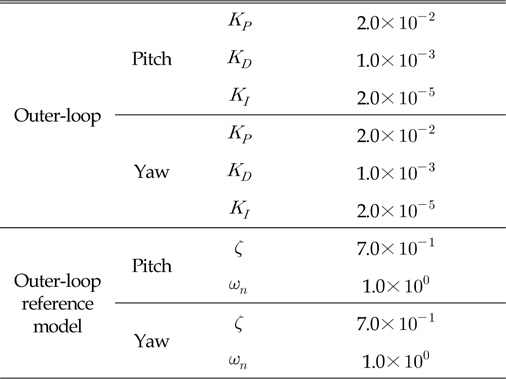
[Table 1] Control gains of inner-loop
Control gains of inner-loop
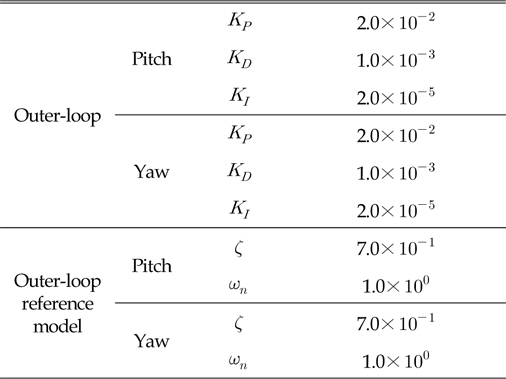
내부루프에서 결정된 제어이득으로 명령각을 잘 추종하고 적응제어신호가 모델링 불확실성을 잘 보상하는 결과를 얻은 후 외부루프의 제어이득을 결정한다. 환경 하중이 없는 상태에서 임의의 심도와 좌우방향 변위의 명령을 입력할 때 만족할 만한 성능을 얻을 때 까지 시행착오법을 통하여 외부루프의 제어이득을 조정한다. 구해진 외부루프의 제어이득은 Table 2에 수록하였다.
[Table 2] Control gains of outer-loop
Control gains of outer-loop
적응제어법칙을 통하여 갱신되는 입력가중변수
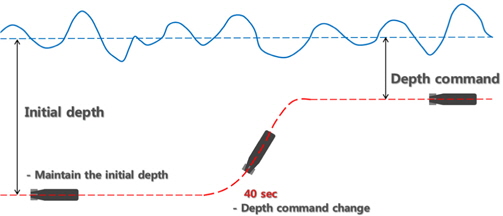
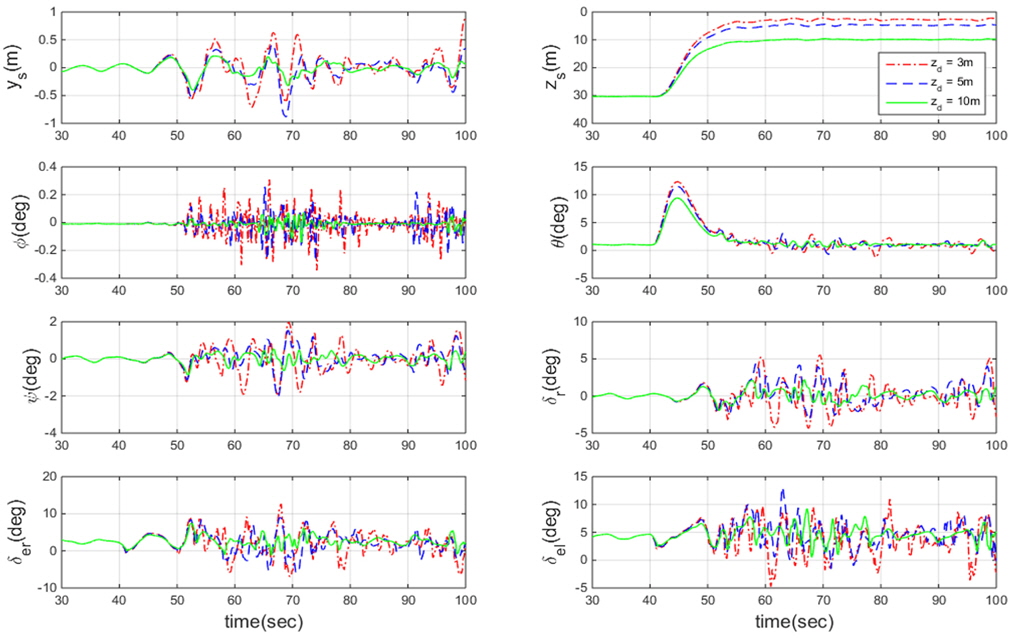
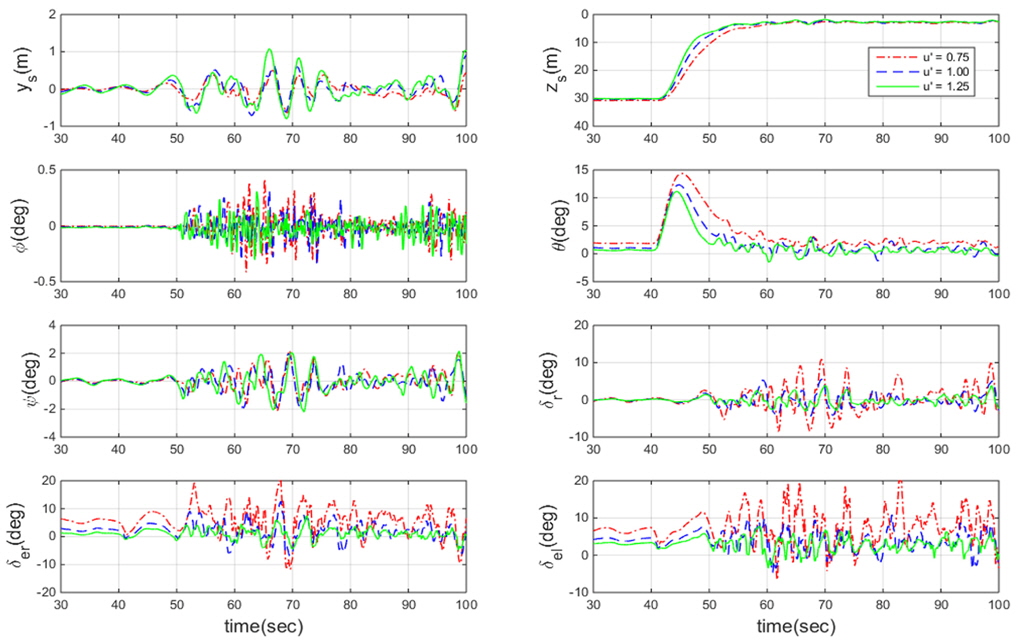
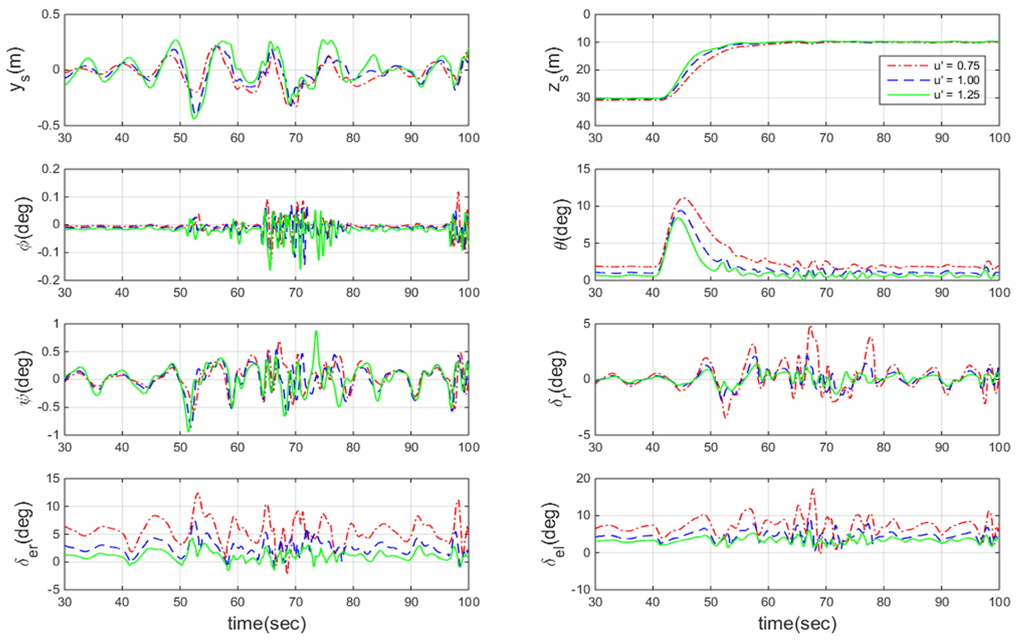
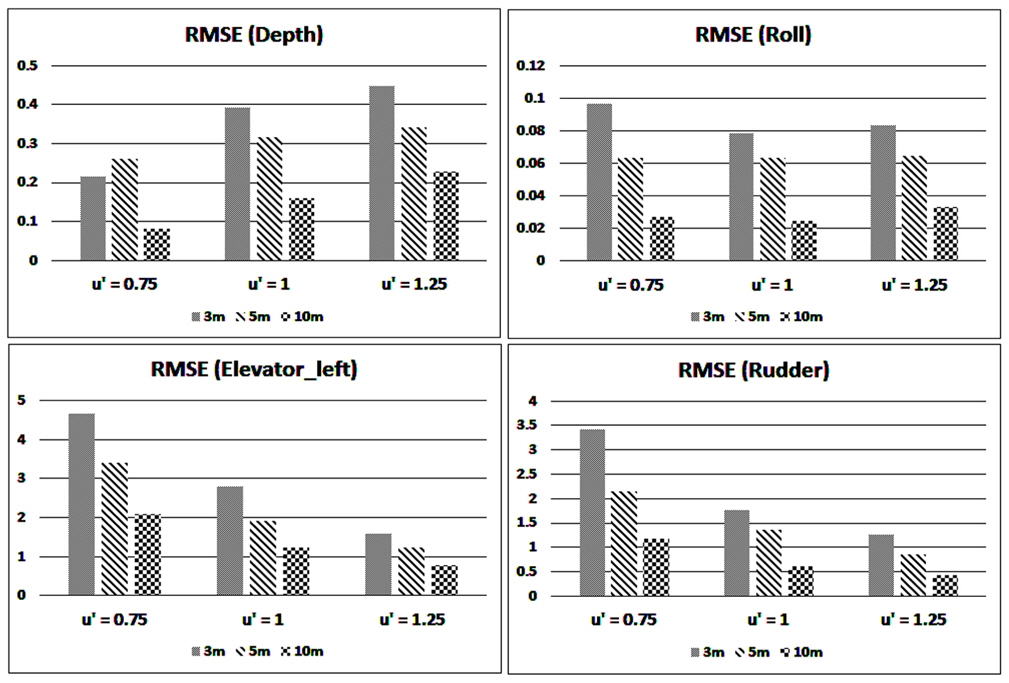
설계된 제어기의 성능을 검증하기 위하여 시뮬레이션을 수행하였다. 시뮬레이션은 30m의 초기심도에서 시작하여 초기심도를 유지하도록 제어하다가 40초 후에 명령심도를 변화시킨다. 해상상태는 Sea state 4이고 파 향은 횡파로 설정하였다. 변화시키는 명령심도는 3m, 5m, 10m 3가지로 설정하였고 운항속도는 3가지 무차원화된 속도조건
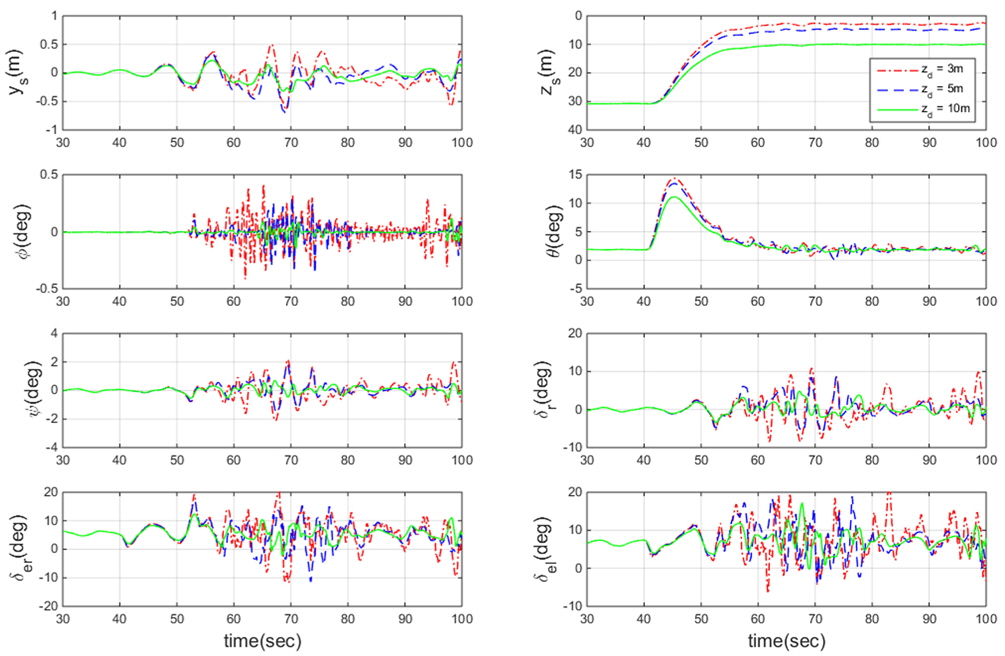
속도 별, 명령심도 별 제어 성능을 비교하기 위한 시뮬레이션 결과를 Fig. 9 ~ Fig 14에 수록하였다. Fig. 9 ~ Fig. 11에는 고정된 속도조건에서 서로 다른 명령 심도를 주었을 때의 제어 시뮬레이션 결과를 한 그래프에 수록하였다. Fig. 12 ~ Fig. 14에는 고정된 명령심도 조건에서 다른 속도로 운항 할 때의 제어 시뮬레이션 결과를 수록하였다. 심도 근처에서의 제어결과 비교가 용이하도록 그림을 30초 이후부터 도시하였다.
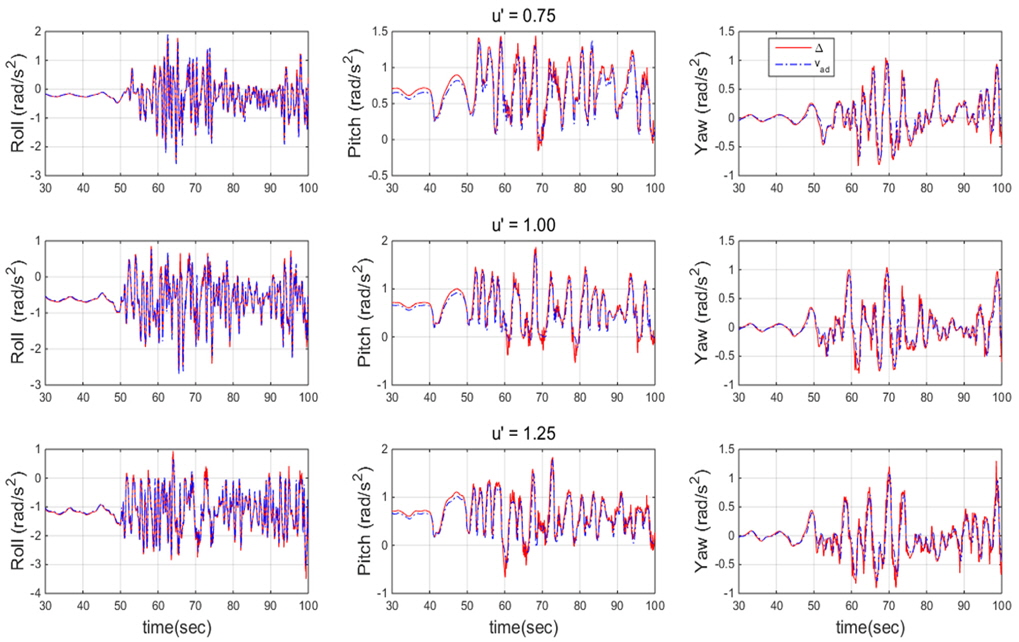
시뮬레이션 결과를 검토해 보면 40초 이후 수면 근처로 이동하면서 증가하는 외란으로 인해 자세를 제어하기 위한 제어판의 조작이 초기심도를 제어할 때 보다 상대적으로 크게 작용하는 것을 알 수 있다. Fig. 9 ~ Fig. 11을 검토해 보면 명령심도가 수면 근처일수록 외란이 커지기 때문에 좌우방향 운동과 횡동요 운동이 증가하는 것을 알 수 있다. 명령심도가 수면 근처일수록 증가하는 운동을 제어하기 위하여 제어판의 조작 또한 증가하는 것을 확인하였다. Fig. 12 ~ Fig. 14를 검토해 보면 몰수체의 운항 속도가 빠를수록 목표 심도에 도달하는 시간이 더 빠른 것을 확인할 수 있다. 속도가 빠를수록 제어판에 걸리는 양력이 증가하기 때문에 속도가 느릴 때 보다 상대적으로 제어판을 덜 조작하며 효율적으로 심도를 제어하는 것을 알 수 있다. 서로 다른 속도조건에서의 종동요 각과 제어판 각의 초기 조건이 다른 것처럼 보이는 이유는 각 속도별 트림이 다르기 때문이다. 시뮬레이션 결과를 종합해 보았을 때 제어기가 속도와 명령심도 조건에 무관하게 좋은 제어성능을 보인다. 수면에 가까울수록 환경하중이 증가하므로 모델링의 불확실성이 가장 큰 조건인 심도 3m일 때 3가지 속도 조건에 대하여 적응제어신호와 모델링 불확실성을 비교하여, 설계된 제어기의 적응제어신호가 모델링의 불확실성을 잘 추정하는지 확인하였다.
Fig. 15는 명령심도가 3m일 때 속도 별 횡동요-종동요-선수동요 방향 적응제어신호와 모델링 불확실성을 의미한다. 결과에서 알 수 있듯 3가지 속도 조건에서 적응제어신호
심도가 깊을수록 파 강제력과 흡입력이 작아지기 때문에 심도오차와 횡동요 오차가 대체적으로 줄어드는 것을 확인할 수 있고 제어판도 적게 작동하는 것을 확인할 수 있다. 운항속도가 클수록 제어력이 커지므로 제어판의 조작이 상대적으로 줄어드는 것을 알 수 있다.
본 논문에서는 수면근처에서 운항하는 몰수체의 심도 제어기 설계를 위하여 파 강제력과 흡인력을 모델링 하였다. 규칙파로 인해 몰수체에 작용하는 파 강제력을 유도하고 선형 이론을 통하여 불규칙파에 의한 힘을 시뮬레이션에 적용하였다. 흡인력을 이중 Rankine 물체를 이용하여 3가지 속도와 다양한 심도에 대하여 계산하였다. 계산 결과 속도가 클수록, 심도가 수면 근처일수록 흡인력이 크게 작용하는 것을 확인하였다. 제어판을 이용하여 위치를 직접적으로 제어할 수 없는 대상 몰수체의 특성을 고려하여 이중루프로 제어기를 구성하였다. 외부루프는 PID제어기법을 이용하였고 몰수체의 동역학과 관련된 내부루프의 경우는 인공신경망을 이용한 적응제어기법을 사용하여 불확실성과 외란에 강건하도록 설계하였다. Sea state 4의 횡파가 작용할 때 3개의 속도와 3개의 명령심도에서 제어 시뮬레이션을 수행하였다. 시뮬레이션 수행 결과 명령 심도가 깊을수록 심도와 횡 방향 오차가 대체적으로 줄어드는 것을 확인하였다. 운항속도가 클수록 제어판에 작용하는 양력이 커지므로 제어판을 적게 조작하며 효율적으로 제어를 하는 것을 확인할 수 있었다.
