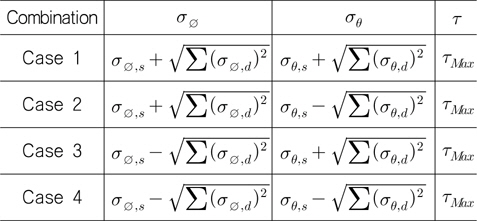Spherical type(구형) LNG 운반선의 구형 탱크는 IMO 가스코드(IGC)에서 독립형 탱크 Type B 방식으로 분류된다.

구형 탱크의 형상은 기하학적으로 가장 안전한 내압력 용기이며 선체와 탱크가 분리되어 있어 충돌이나 좌초 시 가장 안전한 구조이다. Choe, et al. (2001)은 LNG 운반선의 충돌 강도 비교 연구를 통해 구형 LNG 운반선이 멤브레인형 LNG 운반선에 비해 더 많은 충돌에너지를 흡수할 수 있다고 발표한 바도 있다. 또한 화물창에 대한 슬로싱 문제가 없어 파이프 타워 해석에서만 부분적재(partial filling)에 대한 슬로싱 해석을 수행하면 된다 (Noh, 2005). 탱크 내에는 보강재가 없어 균열(crack) 발생을 최소화 할 수 있는 등 많은 장점을 갖고 있으나, 가격이 비싸다는 단점을 가지고 있다.

가격이 비싸기 때문에 초기 견적 시 정도 높은 물량 계산이 필수적이다. 하지만, 매번 유한요소해석을 통한 구조해석을 수행하기에는 많은 시간과 노력이 소요되므로 정도 높은 간이해석법을 정립할 필요가 있다.

구형 탱크의 구조강도 관련 연구는 피로강도 (Nho, et al., 1993), 균열진전 (Nho, et al., 1993), 열 및 저온 (Kim, et al., 1993; Lee, et al., 1998; Nam, et al., 1993) 등의 연구가 비교적 활발히 수행되어 왔으나, 탱크의 초기 설계 및 물량 산출과 관련된 연구는 미진한 편이다. 구형 탱크의 초기 설계를 위한 연구 (Kim, 2000)가 수행된 바 있으나, 하중 조건이 모두 고려되지 못하였고, 유한요소해석으로 수행된 경계조건도 실제 조건과 많이 다르며, 해석 결과와 설계 제작 모델과의 두께 차가 크게 나타났다.

구의 형상은 이론적인 해를 구하기가 용이한 특징이 있어 실제 구조해석 결과와 차이가 적을 것이라고 판단된다. 따라서, 본 연구에서는 이론적인 접근 방법을 기반으로 DNV와 LR 등의 선급 자료를 참고하여 간이해석법 정립을 시도하였다. 또한, 실제 구조해석에서 적용하는 정적 하중 및 동적 하중을 모두 처리할 수 있도록 구성한 것이 특징이며, 정립된 해석법의 결과를 실적선 구형 탱크의 두께 및 중량과 비교하여 그 유용성을 검증하였다.

구형 탱크 내 적용하는 하중 조건은 다음과 같이 크게 네 가지로 구분할 수 있다.

- 만재적하 항해조건(full load seagoing condition) - 비상배출조건(emergency discharge condition) - 탱크시험조건(tank test condition) - 부분적재 항해조건(seagoing condition with partial filling)

가장 대표적이며 복잡한 하중 조건이다. 정적 하중과 동적 하중으로 구성되며, 각 하중의 상세 내용을 Table 1에 나타내었다.

두 가지 조건 즉, 100% 적재(filling) 시와 50% 적재 시로 구분되며, 상세 내용을 Table 2에 나타내었다.

Table 2에서 과압(overpressure)은 탱크 내부에 추가로 가해지는 압력이며, 이 압력은 탱크의 높이(h)에 의존한다. 여기서, ρ는 화물의 밀도, g는 중력가속도를 의미한다. 마진(margin)을 zero로 가정하면, 탱크 바닥에 가해지는 액체 화물을 포함한 압력은 100% 적재 시와 50% 적재 시 모두 같을 것이다. 하지만, 탱크 꼭대기 부위의 압력은 50% 적재 시가 100% 적재 시보다 2배 더 크게 나타남을 알 수 있다.

Table 3에 나타낸 바와 같이 두 가지 조건으로 구분되며, 일반적으로 두 조건 중 물을 50% 채우는 조건이 탱크 바닥에서는 압력이 더 크지만, 탱크의 상부에서는 압력이 더 작다.

이 조건은 탱크의 중하부 영역이 좌굴에 취약하여 중하부 영역의 두께를 결정하기 위해 사용되며, 하중 조건을 Table 4에 나타내었다.

응력 조합의 목적은 최대등가응력을 구하는 것이다. 최대등가응력을 구하기 위해서 자오선방향 응력(σ_∅), 원주방향 응력(σ_θ ), 전단응력(τ)을 정적 응력과 동적 응력 항으로 구분하고, 정적 응력 항과 동적 응력 항을 모두 조합하여 최대값을 찾아낸다.

경우의 수는 모두 8가지이나, 등가응력(σ_e)을 구하는 식 (1)에서 보면 전단응력 항은 부호에 상관없이 최대값을 선택하고, 4가지 경우를 조합해도 최대등가응력을 구할 수 있다. 최대등가응력을 구하기 위한 응력조합을 Table 5에 상세히 나타내었다.

앞에서 언급한 바와 같이 전단응력의 경우, 두 합성 응력 과 중 절대값이 큰 값을 τ_Max라 하면 Table 5와 같이 네 가지의 응력 조합을 계산할 때, 전단응력 항은 항상 τ_Max를 대입하면 되며, 그 이유는 식 (1)의 형태에 기인한다. σ_∅,s와 σ_θ,s는 정적 응력 항을 의미하며, σ_∅,d와 σ_θ,d는 동적 응력 항을 의미한다.

구형 탱크는 일반적으로 8개의 영역으로 구분되며, Fig. 1과 같이 상부 및 하부가 각각 4개의 영역으로 구성된다.

8개의 영역은 지배적인 하중 형태에 따라 4개의 그룹으로 분류할 수 있다. 하부(Zone 1, Zone 2), 중하부(Zone 3, Zone 4L), 중상부(Zone 4U, Zone 5) 및 상부(Zone 6, Zone 7)로 구분되는데, 각 영역의 지배 하중 조건을 Table 6에 나타내었다.

상부(Zone 6, Zone 7)의 경우를 보면 탱크의 높이에 따라 비상배출조건과 탱크시험조건 중 지배적인 하중 조건이 결정되지만, 하부(Zone 1, Zone 2)의 경우는 만재적하 항해조건과도 비교해 보아야 한다. 비상배출조건과 탱크시험조건은 가속도와 무관한 조건이지만, 만재적하 항해조건은 가속도에 따라 탱크에 큰 응력을 발생시킬 수 있기 때문이다. 특히, 1번 탱크(선수 쪽 첫 번째 탱크)의 경우는 위치상 가속도의 크기가 상당히 크다.

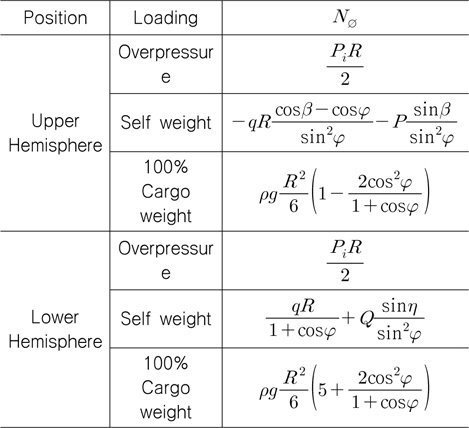
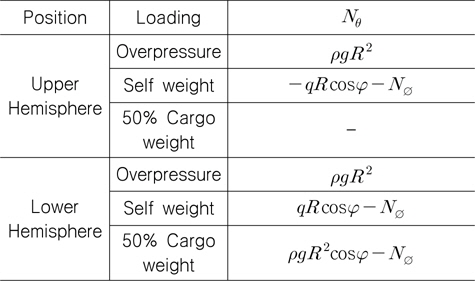
구형 탱크에 발생하는 힘은 이론적으로 표현하기 용이하며, 2장에 서술한 하중 조건들에 의해 발생하는 힘을 이용하면 허용 응력을 넘지 않는 최소의 탱크 두께를 계산할 수 있다. 탱크에 발생하는 힘(N/mm)인 자오선방향 힘(N_∅), 원주방향 힘(N_θ ), 전 단력(N_∅θ)을 Fig. 2에 정의된 기호를 통해 나타내고자 한다.

Fig. 2에서 P는 돔(dome)과 파이프 타워에 의한 단위길이당 힘을, Q는 파이프 타워에 의한 단위길이당 힘을 의미한다.

만재적하 항해조건의 경우 탱크에 작용하는 정적인 힘 중 과압, 자중, 화물 중량은 이론적인 수식으로 표현하기 용이하다. 본 연구에서는 과압과 자중에 대해서만 수식의 유도과정을 설명하고자 한다.

먼저, 일정한 내압(P_i)을 받는 구에서의 자오선방향 힘을 Fig. 3과 같은 상반구에서의 힘의 평형방정식으로 유도해 보면 다음과 같다.

내압의 수직방향 합력은 와 같고, 자오선방향 힘의 수직 방향 합력은 2πr₀sinφN_∅라 할 수 있다. 따라서, 힘의 평형 방정식을 식 (2)와 같이 나타낼 수 있다.

식 (2)에서 양변을 πr₀로 나누고, r₀ = Rsinφ를 대입하면, 식 (3)과 같은 내압에 대한 자오선방향 힘을 수식으로 나타낼 수 있다.

또한, Timoshenko and Woinowsky-Krieger (1959)는 축대칭 하중을 받고 회전체 형상을 갖는 외판(shell)에서의 자오선방향 힘과 원주방향 힘의 평형방정식을 자오선상 임의의 한 점에서의 자오선 곡률 반경(r₁), 그 점과 자오선의 수직선이 회전축과 만나는 점까지의 거리(r₂), 자오선에 수직인 단위 면적당 외력(F_z)에 대한 관계로 식 (4)와 같이 유도하였다.

식 (3)을 식 (4)에 대입하면, 원주방향의 힘을 구할 수 있다. 구의 균일 내압 문제에서 r₁ = r₂ = R이고, f_z = −P_i이므로 식 (4)는 식 (5)와 같이 되어, 원주방향의 힘은 자오선 방향의 힘과 같음을 확인할 수 있다.

하반구에서의 두 힘의 유도 과정도 같은 결과를 얻게 되며, 식 (3)과 (5)를 통해 일정한 내압을 받는 구에서의 자오선방향 힘과 원주방향 힘은 구의 어느 위치에서나 그 크기가 같음을 알 수 있다.

다음은 자중에 대한 상반구에서의 힘의 계산식 유도 과정을 설명하고자 한다. Fig. 4는 상반구에서 자중(W)에 대한 자오선 방향 힘을 유도하기 위해 나타낸 그림이다.

자중과 같은 방향의 단위길이당 자오선방향 힘은 N_∅sinφ이며, 전체적인 힘은 2πr₀N_∅sinφ이다. 또한, 돔과 파이프 타워에 의한 단위길이당 힘 P에 의한 전체적인 힘은 2πPRsinβ이다.

식 (6)에 r₀ = Rsinφ를 대입하면 식 (7)과 같이 나타낼 수 있다.

자중은 단위면적당 중량 q를 이용하여 기술하면 식 (8)과 같이 나타낼 수 있다.

식 (7)에 식 (8)을 대입하여 양변을 2πRsin²φ로 나누면 식 (9)와 같이 자오선방향의 힘을 구할 수 있다.

이 문제에서는 f_z = qcosφ이므로 이를 식 (4)에 대입하면 식 (10)과 같은 원주방향 힘을 구할 수 있다.

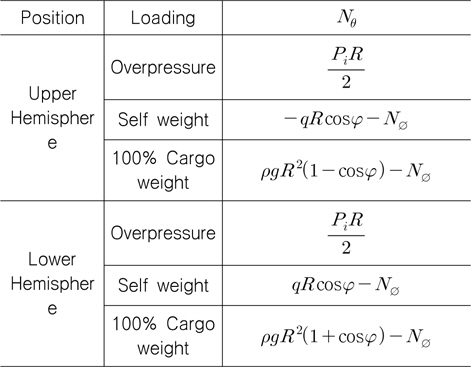
화물 중량에 대한 자오선방향 힘과 원주방향 힘의 유도과정은 생략하고 결과만을 Table 7과 8에 나타내었다.

정적 힘은 Z축에 대해 축대칭(axisymmetric) 형태를 유지하지만, 동적 힘은 수평방향의 가속도에 의해 Z축이 아닌 경사축에 대한 축대칭을 형성한다.

액체 화물의 횡가속도(α_H)에 의해 발생하는 압력 P_H를 유도하면 식 (11)과 같이 나타낼 수 있다.

식(11)을 두 항으로 분리하면 위치에 따라 일정한 압력 P₁과 위치에 따라 변하는 압력 P₂로 각각 식 (12), 식 (13)과 같이 나타낼 수 있다. 전자는 Fig. 5의 왼쪽 그림, 후자는 오른쪽 그림과 같다.

중요한 사실은 최대 동적 힘이 작용하는 위치라고 할 수 있다. 일반적으로 선체 길이 방향인 X방향의 가속도보다 선체 폭 방향인 Y방향의 가속도가 훨씬 크기 때문에 Fig. 6에 나타낸 바와 같이 선체의 중심선(center line)에서 90° 위치한 지점에서 최대 힘이 작용한다.

최대 힘이 작용하는 위치에서는 X방향의 가속도에 의해서 발생하는 압력 중 위치에 따라 변하는 압력 항은 N_∅와 N_θ에 영향을 주지 않고, N_∅θ만 발생시킨다. 또한, Y방향의 가속도에 의해서 발생하는 압력 중 위치에 따라 변하는 항은 N_∅와 N_θ에 영향을 주지만, N_∅θ에는 아무런 영향도 주지 않는다. 최대 힘이 작용하는 위치에서의 동적인 힘을 Table 9에 상세히 나타내었다. a_xc와 a_yc는 식 (12)의 괄호 속의 형태를 의미한다. 예를 들어,

선체와 탱크의 상호작용력(interaction force)은 이론적인 수식으로 표현하기 어려워 과거 구조해석을 통해 얻은 데이터 값들을 적용하였다.

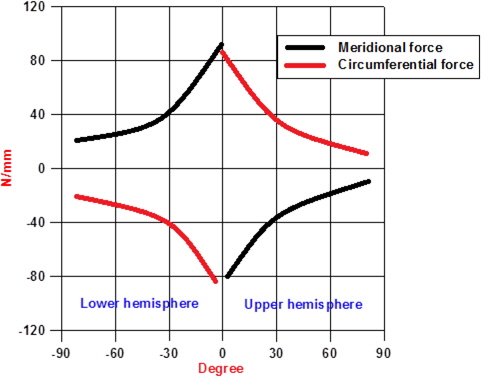
Fig. 7은 상호작용력의 전형적인 그래프로서 구형 탱크의 적도(equator) 부에서 큰 값을 나타내고 상부와 하부로 가면서 점점 그 값들이 줄어드는 경향을 보이고 있다.

파랑중 굽힘모멘트에 의한 상호작용력 역시 같은 경향을 나타내고, 값의 크기는 정수중 굽힘모멘트에 의한 값보다 약 2배 정도 크게 나타난다.

상호작용에 의한 자오선방향 힘과 원주방향 힘은 부호가 반대이며 크기는 거의 비슷함을 알 수 있다.

비상배출조건의 경우는 일반적으로 50% 적재의 경우가 100% 적재의 경우보다 탱크 내부 전체에 더 큰 압력을 가하고 있어, 더 보수적인 조건인 50% 적재의 경우만 고려하였다.

비상배출조건에서는 동적 조건을 고려하지 않으므로, 상호작용력을 제외하면 탱크에 작용하는 정적인 힘은 Z축에 대한 축대칭 형태를 유지한다.

만재적하 항해조건의 경우와 마찬가지로 탱크에 작용하는 정적인 힘 중 과압, 자중, 화물 중량은 이론적인 수식으로 표현하기 용이하며, 이를 Table 10과 11에 나타내었다.

선체와 탱크의 상호작용력은 만재적하 항해조건의 경우와 마찬가지로 이론적인 수식으로 표현하기 어려워 과거 구조해석을 통해 얻은 데이터 값들을 적용하였다. 다른 점은 비상배출조건에서는 정수중 굽힘모멘트에 의한 상호작용력만 고려하면 된다.

탱크시험조건의 경우, 일반적으로 탱크의 상부에서는 탱크를 비우는 조건이 더 보수적이고, 탱크 바닥에서는 물을 50% 채우는 조건이 더 보수적이다. 따라서, Zone 1과 Zone 2의 두께 계산 시는 물을 50% 채우는 조건을, Zone 6과 Zone 7의 두께 계산 시는 탱크를 비우는 조건을 적용하였다.

탱크시험조건에서도 동적 조건을 고려하지 않으므로, 상호작용력을 제외하면 탱크에 작용하는 정적인 힘은 Z축에 대한 축대칭 형태를 유지한다.

탱크에 작용하는 정적인 힘 중 과압, 자중, 화물 중량은 이론적인 수식으로 표현하기 용이하며, 이를 Table 12와 13에 나타내었다.

탱크시험은 조선소 내 정수 중에서만 수행되므로 선체와 탱크 상호작용력은 비상배출조건에서와 같이 정수중 굽힘모멘트에 의한 상호작용력만 고려한다.

액체 화물의 부분 적재로 탱크에 작용하는 최대 압축력을 얻기 위해 스큐각(skew angle, ω)을 0°에서 시작하여 1°씩 증가시켜 최대 압축력을 주는 스큐각을 결정한다. 스큐각이 증가할수록 겉보기 횡가속도(apparent transverse acceleration, )는 점점 감소하게 되지만, 원주방향 힘(N_θ)은 적하율(filling ratio)이 증가하여 점점 증가하게 된다.

압축력은 로 나타낼 수 있고, α_R은 합가속도(resulting acceleration)를 의미한다. 합가속도는 겉보기 횡가속도와의 관계를 이용해 구할 수 있다.

두 가속도의 관계는 Fig. 8에 나타낸 타원으로 정의된 가속도 타원(acceleration ellipse)의 관계에서 구할 수 있다. 용이한 이해를 위해 모든 가속도 성분을 중력가속도 g로 나눈 무차원 값을 적용하면 타원의 식은 식 (14)와 같이 나타낼 수 있고, x, y를 삼각함수로 표현하면 식 (15)가 된다.

식 (15)를 정리하면, 식 (16)과 같은 α_R에 대한 2차 방정식으로 나타낼 수 있다.

결국, 합가속도는 식 (17)과 같이 근의 공식으로 쉽게 계산할 수 있다.

스큐각의 범위는 합가속도가 점점 증가하여 중근을 가질 때가 최대값이 되므로 식 (18)을 만족하는 ω를 구하면 된다. 중근을 갖는 경우인 식 (15)을 정리하면 식 (19)가 되고, 식 (19)의 양변을 로 나누어서 정리하면 식 (20)이 된다.

따라서, 스큐각의 범위는 식 (21)과 같이 나타낼 수 있다.

압축력()은 스큐각이 커질수록 점점 증가하다가 어느 각도를 넘어가면 다시 감소한다. 최대가 되는 순간의 값을 구하고, 그 때의과 N_∅α_R을 각각 N_θ1과 N_∅1으로 정의한다.

또한, 추가 되는 압축력인 상호작용력과 0.05bar의 외압도 고려해야 한다. 좌굴 계산 영역인 Zone 3과 4L은 Fig. 5에서 알 수 있듯이 상호작용에 의한 원주방향 힘이 압축력으로 작용하고 있으며, 자오선 방향의 힘은 인장력으로 작용하고 있다.

최대 설계 압축력(N_θ0)과 최대 설계 인장력(N_∅0)은 식 (22)와 (23)처럼 나타낼 수 있다.

하중 계수(load factor) 및 좌굴 표준(buckling criterion)은 Det Norske Veritas (1997) 자료 내용을 그대로 적용하였다.

간이해석법을 검증하기 위해 적용한 실적선은 탱크 직경이 40.46m인 137K 구형 LNG 운반선으로 주요 제원 및 특성을 Table 14에 나타내었고, 실제 구조해석에 사용된 설계 가속도는 Table 15에 나타내었다. 각 탱크마다 위치가 달라서 설계 가속도가 모두 다르게 나타나지만, 제작상의 이유로 가장 가속도가 큰 탱크인 1번 탱크는 별도로 설계하고, 2~4번 탱크는 서로 가속도를 비교하여 제일 큰 값을 설계 가속도로 선정하여 동일하게 설계한다

실적선 구형 탱크의 각 영역은 Fig. 9에서와 같이 상반구와 하반구가 적도부를 중심으로 정확히 대칭이며, 각 영역의 시작과 끝을 파이프 타워의 중심선에서의 각도로 표시하였다.

동일한 비교를 위해 실적선의 두께 결정에 적용된 규정을 그대로 적용하였다. 두께 결정 규정은 다음과 같다.

(1) 모든 두께는 선급에서 규정하는 탱크 최소두께 (R/750) 이상으로 규정한다. (2) 인접 지역의 두께 비(두꺼운 두께/얇은 두께)는 1.4 이하로 규정한다. (3) 제작상의 편의성을 고려하여 동일한 형상의 적도부 제작을 위해 Zone 4L과 Zone 4U의 두께는 가장 두꺼운 1번 탱크의 두께를 적용한다.

3번째 항목에서 언급한 적도부 형상을 Fig. 10에 나타내었다. 적도부는 상부는 Zone 4U와 하부는 Zone 4L과 Skirt와 연결되며 적도부의 두께(t_eq)는 Zone 4L과 Skirt 부의 두께에 영향을 받으며, 일반적으로 150mm가 넘는 상당히 두꺼운 구조이다.

간이해석법을 통해 각 탱크의 요구 두께(required thickness)를 계산한 결과를 Table 16과 17에 나타내었다.

동적 가속도를 고려하는 만재적하 항해조건을 지배 하중 조건으로 갖는 영역에서 1번 탱크의 두께 요구치가 다른 탱크에 비해 4~6mm 크게 나타나며, 비상배출조건과 탱크시험조건은 동적 가속도를 고려하지 않으므로 모든 탱크에서 두께 요구치가 같게 나타난다. 좌굴에 취약한 Zone 3과 4L 영역은 1번 탱크의 두께가 다른 탱크에 비해 1mm 증가하였다.

Zone 6의 두께는 모든 탱크가 29mm로 나타나지만, 두께 결정 규정 2번째 항목에 의해 1번 탱크에서는 31mm로 설계 되어야 두께비가 1.4이하가 된다. 또한, 두께 결정 규정 3번째 항목에 의해 Zone 4L과 Zone 4U의 두께는 1번 탱크의 두께와 다른 탱크의 두께를 같은 값으로 적용하였다.

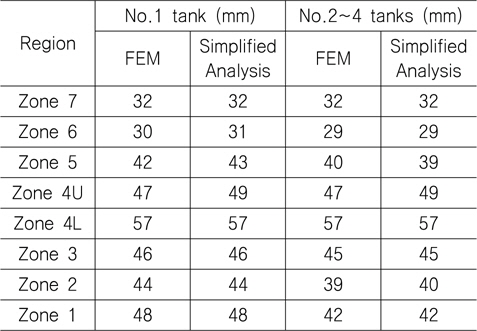
Table 18은 실적선의 탱크 두께와 본 연구의 간이해석법의 결과를 비교한 것이다. 모든 탱크의 각 영역 두께가 실선과 거의 일치함을 알 수 있다

가장 복잡한 하중 조건인 만재적하 항해조건을 지배 하중 조건으로 갖는 Zone 4U와 5 영역이 유한요소해석과 가장 큰 차이를 보이고 있으나, 그 차이도 최대 2mm 정도이다

두께 계산 결과로 정립된 해석법의 정도가 높다고 판단되어 물량 계산을 통해 유한요소해석과의 오차율을 계산해 보았다.

Table 19는 실적선의 탱크 중량과 본 연구의 간이해석법으로 구한 중량을 비교한 것이다. 1번 탱크의 중량은 약 7ton의 차이를 보이며, 다른 탱크는 약 1ton의 차이를 보인다. 총중량 계산 결과 및 오차율은 다음과 같다.

총중량 비교 FEM: 576 + (585×3)=2331ton Simplified analysis: 583 + (586×3)=2341ton 오차율 계산 Error rate(%) = 10/2331×100 = 0.4%

1번 탱크의 중량차이가 가장 크게 나타나지만, 그 오차율도 1.2% 에 불과하며, 총중량에 대한 오차율은 0.4%로 나타나 간이해석법이 매우 유용한 방법임을 확인할 수 있었다.

본 연구는 실제 구조해석에서 적용하는 정적 하중 및 동적 하중을 모두 처리할 수 있도록 이론식에 기초한 간이해석법을 정립한 바 다음과 같은 결론을 얻었다.

실적선인 137K 구형 LNG 운반선의 탱크 설계에 적용한 결과, 모든 탱크의 각 영역 두께가 상호간에 거의 일치함을 확인할 수 있었으며, 총중량도 거의 일치함을 확인하였다.

초기 견적 시 간이해석법을 적용하면, 많은 시간을 소요하는 구조해석 없이 정도 높은 탱크 물량을 산출할 수 있을 것으로 사료된다.