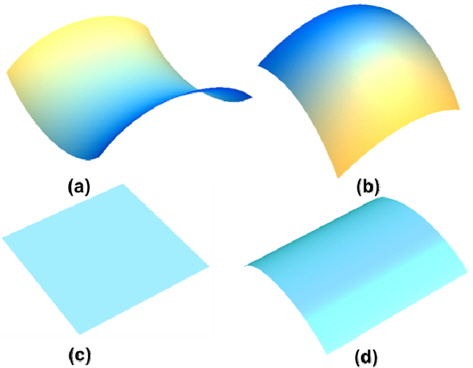
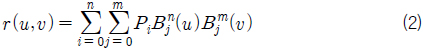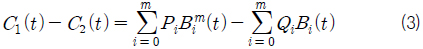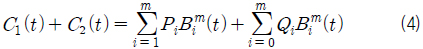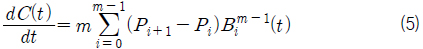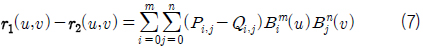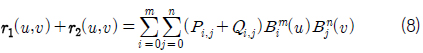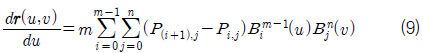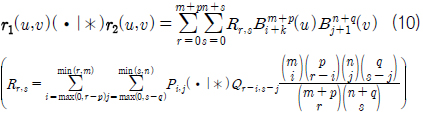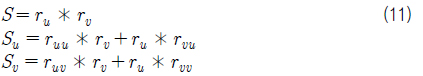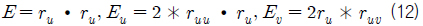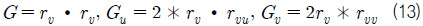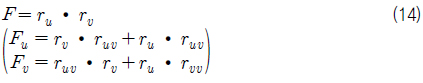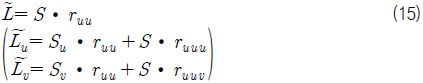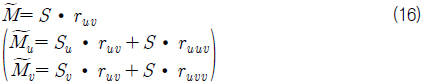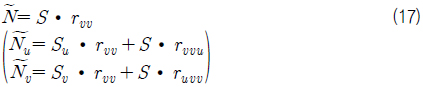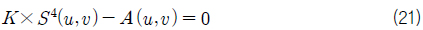선체의 선수와 선미를 이루는 선체 외판 곡면은 여러 가지 형태의 곡면으로 구성된다. 이러한 선체 외판을 구성하는 곡면을 분류해 보면 전형적인 형태(안장형, 볼록형, 실린더형, 평면형)와 복합적인 형태로 나눌 수 있다. 외판 곡면의 효율적인 생산을 위해서 곡판의 형태에 맞는 효율적인 가공방법의 적용이 필요하다.

Kim, et al. (2006)는 선박 건조 비용 측면에서의 곡면 형상에 따른 가공비 산정에 의한 경제성 평가를 위한 사전 연구로서 신경망을 이용한 학습적 곡판 분류 기법에 대한 연구를 수행했다. 곡판 분류를 위해 가우스 곡률을 이용해서 1차, 2차, 3차 곡판을 분류하였다. 1차는 평면형, 2차는 실린더형, 3차는 여러 형태가 혼합된 형태이다. 분류방법으로는 신경망을 이용하여 입력으로 선체외판에서 분할된 사각형 곡판을 출력으로 1차, 2차, 3차 곡판을 사용했다. 그리고 신경망의 학습을 위해 곡면을 몇 개의 절점으로 샘플링하고 각 절점에서 가우스 곡률의 분포 비율을 이용했다.

Noh and Shin (2009)는 곡가공 프로세스를 고려한 곡판 분류에 관한 연구를 수행했다. 곡가공 프로세스를 시스템 엔지니어링 측면에서 분석하고 곡판의 형태와 맞는 곡가공 프로세스를 결정했다. 곡판을 사각형 곡면으로 모델링하여 표준형상(안장형, 볼록형, 실린더형, 평면형)의 분포비율을 이용해 곡판의 생산에 필요한 가공공정을 분류했다.

절점곡률이나 표준형상의 분포를 이용하여 곡판을 분류하는 과정에서는 곡면을 분할하여 그 요소의 절점이나 중앙점에서의 곡률을 통해 곡판의 가공공정을 분류한다. 분류할 곡면을 동일한 크기의 요소로 분할한다면 큰 문제가 없지만 동일한 크기의 요소로 분할되지 않은 상태에서 곡률의 분포는 실제 곡면을 반영하지 못하게 된다. 그런데 현실적으로 곡면을 동일한 크기의 요소로 분할하는 것은 어려운 부분이다. 그렇기 때문에 앞의 방법은 정량적인 분류 방법이라 하기에 부족하다. 또 같은 이유로 분류의 대상인 곡면이 분할정도(해상도)에 따라 곡판의 분류결과가 달라질 수 있다. 그러나 절점곡률이나 표준형상을 이용한 Kim, et al. (2006) 과 Noh and Shin (2009)는 요소의 크기와 분할해상도에 변화가 분류결과에 미치는 영향에 관한 논의는 없었다.

본 연구는 기존연구의 한계점을 해결하기 위해 특징영역을 구분하는 등곡률선(isocurvature line, 곡률이 동일한 값을 갖는 곡면상의 곡선)을 직접 계산하는 방법에 대해 논의한다.

등곡률선을 찾는 방법에 대한 기존의 연구는 금형의 가공과 관련하여 활발히 진행되었다. 공작기계의 가공순서를 계획하기 위해서 가우스 곡률의 부호가 변화하는 지점을 정확하게 찾아야 하기 때문이다. 또한 금형가공을 하는 중에 발생할 수 있는 Over-Cut (Meakawa & Patrikalakis, 1994)을 방지하기 위해 가우스 곡률이 0이 되는 지점에서 툴을 교체해야 하는데, 이 때도 등곡률선을 계산할 필요가 있다.

등곡률선을 계산하는 과정은 크게 두 가지 과정으로 나누어 볼 수 있는데, 곡률곡면을 계산하는 과정과 실제로 등곡률선을 찾는 과정 이다.

Elber (1992)는 상징연산(symbolic operation)을 응용하여 곡선/곡면과 관련한 다양한 기하문제를 수치적 방법을 대체하는 새로운 방법을 제안했다. 그 응용 사례로 곡면의 곡률곡면(곡률값이 메게변수 곡면의 도메인 상의 점으로 표현된 곡면)을 상징연산을 통해 직접 얻었고, 곡률곡면에서 등곡률선을 분할 방법을 통해 계산했다. 계산된 등곡률선을 활용해 5축 공작기계에 최적화된 툴 경로를 계산했다.

Meakawa and Patrikalakis (1994)는 상징연산을 이용하여 생산을 위한 곡선/곡면의 형상질의(shape interrogation)에 관한 연구를 수행했다. 가우스 곡률의 등곡률선을 찾기 위해 상징연산으로 곡면의 곡률곡면을 계산하고 Interval Projected Polyhedron (Sherbrooke & Patrikalakis, 1993)를 이용해 시작점을 계산 한 다음, 상미분방정식(runge-kutta)을 이용해 등곡률선을 계산했다.

Nam (2003)은 곡면의 형상질의 대한 연구로 가우스 곡률을 계산하여 계산된 값을 곡면으로 보간하여 곡률곡면을 얻었고 평면과 곡률곡면의 교차계산으로 등곡률선을 계산했다. 교차를 통해 얻어진 등곡률선의 품질은 곡률곡면을 얼마나 정확히 계산하느냐에 달려있다. 따라서 곡률의 분포가 단순한 곡면의 경우는 매우 효율적일 수 있으나 곡률의 분포가 복잡한 곡면의 경우 적용하기 어렵고 곡률곡면을 계산하는 과정에서 곡면의 곡률을 제대로 반영하지 못할 수도 있다.

Seong (2005)은 식의 개수보다 변수가 한 개에서 두 개 많은 특수한 형태의 문제를 풀이할 수 있는 방법을 제안했다. 곡률곡면과 등곡률선을 계산한 기존연구와 달리 곡률곡면과 유사한 형태의 식을 계산하는 방법에 관해 연구했다. 그는 식과 도메인(해를 포함하고 있는 구간)이 존재하는 경우 도메인을 분할해 서브 도메인이 해를 포함하는 경우 서브도메인간의 연결관계를 이용해서 해를 계산했다. 이때 서브도메인간의 연결관계는 해의 유일성(주어진 도메인에는 해가 존재하는 성질)을 확인하는 조건이 된다.

본 연구는 가우스 곡률에 대한 등곡률선을 계산하는 것이 목적이며 그에 대한 정확한 계산을 위해 Elber (1992)과 Meakawa and Patrikalakis (1994)가 사용한 상징연산을 통해 곡률곡면을 계산하고, 등곡률선의 강건한 계산을 위해 Seong (2005)이 제안한 방법을 사용한다.

본 논문의 구성은 다음과 같다. 상징연산을 통한 곡률곡면의 계산, 곡률곡면을 이용한 등곡률선의 계산, 등곡률선으로 구분된 곡률 영역의 면적 계산, 적용 결과, 결론 및 향후 연구 과제로 구성된다.

곡선/곡면의 기하학적인 정보를 찾기 위해서는 최소 한 개의 주어진 점을 기준으로 상미분방정식이나 기타의 추적 기법을 통해 찾고자 하는 모든 점을 계산한다. 수치적 추적 기법은 시간에 대한 효율성 측면에서 장점이 있어 다양한 기하문제에 적용된다. 반면 사용자가 지정한 공차에 계산결과가 민감하게 반응하며, 계산 과정 중 발산할 가능성이 있으므로 예외상황에 대한 처리가 필수적으로 요구된다. 기하문제 중에서도 특히 곡면 간의 교선을 추적하는 문제의 경우, 상용 시스템에서 제공하는 기능이 두 곡면이 점으로 접하는 경우나 면으로 접하는 경우에 대해서는 만족할 만한 성능을 보이지 않는다. 따라서 기하문제를 계산하면서 효율성과 강건성을 동시에 만족하는 방법에 대한 연구가 활발히 진행되고 있다 (Ko, 2010).

이러한 수치적 방법의 한계를 해결하기 위한 방법 중 하나로 상징연산이 있다. 상징연산을 이용한 기하계산의 경우 기하문제를 대수적인 문제로 변환하여 계산함으로써 계산결과의 누락이나 에러를 방지할 수 있다. 따라서 근본적으로 강건성이 보장된다고 할 수 있다. 또 Rounded Interval Arithmetic(RIA) (Meakawa & Patrikalakis, 1994)를 적용하게 되면 Floating Point Arithmetic를 사용할 때 유효숫자로 인해 발생하는 문제(round off)를 해결 할 수 있다. 즉, RIA를 사용하면 사용자가 해의 범위를 지정하여 계산 결과가 발산하지 않도록 할 수 있게 된다.

반면 상징연산을 통해 해를 찾는 과정의 대부분은 해가 포함되지 않은 Redundancy Domain을 제거하는 과정으로, 수치적 추적기법에 비해 계산시간의 효율성은 다소 떨어진다. 하지만 컴퓨터 성능의 지속적인 향상과 다양한 계산가속화기법의 연구로 인해 현재는 충분히 다양한 문제에 적용 가능하다고 볼 수 있다.

현재까지 연구된 상징연산은 B-spline, Bezier 곡선/곡면을 대상으로 한다. 상징연산은 곡선/곡면간의 연산이므로 상징연산 후 얻어지는 곡선/곡면은 필연적으로 많은 조정점을 가지게 된다. 그러므로 컴퓨터의 성능이나 저장공간 등을 고려하여 어떤 형태의 곡선/곡면 상징연산에 사용할지 결정해야 한다.

이와 관련해 Sherbrooke and Patrikalakis (1993)는 계산과 저장의 효율성 면에서 대체로 Bezier 곡선/곡면이 더 좋은 것으로 밝히고 있다. 따라서 본 논문에서는 Bezier 곡선/곡면의 상징 연산을 이용한다.

Bezier 곡선/곡면이 도메인을 공유하는 경우 특정연산(미분, +, -, vector product, scalar product)을 하면 새로운 형태의 Bezier곡선/곡면식이 계산된다.

식 (1)의 C(u)과 식 (2)의 r( u, v )는 각각 Bezier곡선/곡면을 나타내는 식으로 P_i과 P_i,j는 곡선/곡면을 표현하는 조정점이고 과 는 Bezier곡선/곡면에서 조정점의 영향도를 조합하여 곡선/곡면상의 점을 계산하는 기저함수이다 (Patrikalakis & Maekawa, 2002).

식 (3)~식 (4) 동일한 도메인과 동일한 차수를 공유하는 두개의 Bezier 곡선 사이에 성립하며 두 곡선의 합과 차를 표현하는 연산이다. 식 (7)~식 (8)도 동일한 도메인과 동일한 차수를 공유하는 두 개의 Bezier 곡면 사이에 성립하며 두 곡면의 합과 차를 표현하는 연산이다. 식 (5)와 식 (9) 곡선/곡면의 미분 연산이다. 식 (6)와 식 (10)은 서로 같은 도메인을 공유하고 서로 다른 차수를 가진 곡선/곡면인 경우 성립하면 곡선/곡면간의 스칼라연산과 벡터연산을 표현한다. 자세한 유도과정의 내용은 Elber (1992)을 참고하기 바란다.

식 (11)는 곡면의 법선벡터 곡면을 표현하는 식이고, 식 (11)에서 사용한 r_u, r_v 은 파라메트릭 곡면식을 각각의 매계변수 방향으로 한번씩 편미분한 식이다. 식 (12), (13), (14)는 곡면의 first fundamental form이고, 식 (15), (16), (17)는 곡면의 second fundamental form이다. 식 (18)은 곡면의 법선 벡터의 크기를 표현하는 식이다. 식 (19)의 A는 second fundamental form의 행렬식(determinant)이다. 식 (20) 가우스 곡률을 나타내는 식이다. 하지만 식 (20)은 상징연산이 지원하지 않는 나누기 연산이 포함된 식이므로 곡률곡면을 계산하기 어렵기 때문에 상징연산을 적용할 수 있는 형태로 바꾸어 식을 사용해야 한다. 따라서 식 (20)은 식 (21)와 같이 변환했다. 이때 식 (20)의 K는 찾고자 하는 가우스 곡률 값이다. 식 (21)를 통해 3차 Bezier 곡면을 가우스 곡률의 곡률곡면으로 바꾸면 u, v의 차수가 각각 20인 Bezier곡면의 형태로 바뀌게 된다. 식 (11) ~ 식 (21)는 Meakawa and Patrikalakis (1994)의 연구에서 참조했다.

메게변수 형태의 곡면이 주어지는 경우 상징연산을 적용하여 가우스 곡률을 나타내는 곡률곡면을 얻을 수 있다. 곡률곡면에서 등곡률선을 찾아야 하는데 이는 식 (21)이 0인 u, v를 찾는 것이다. 곡률곡면에서 동일한 값을 갖는 선을 추적하는 문제(1-manifold)는 식이 한 개 이고 변수가 두 개인 비선형 방정식이다. 식 (21)의 형태를 보면 음 함수의 형태를 띠고 있다. 따라서 기존의 음 함수를 가시화하는 방법을 응용하여 해를 계산할 수 있다.

Seong (2005)은 기하문제를 상징연산을 통해 변환하게 되면 변환된 식의 형태가 음 함수라는 점에 착안하여 음 함수 모델을 가시화 하는 방법인 Matching method와 Dual Contouring을 사용하여 비선형방정식을 계산할 수 있는지 연구했다. 그 결과 도메인(해를 포함하고 있는 구간)의 개수가 3개 이상의 고차원이 존재하는 기하문제에 Dual Contouring을 적용할 수 있음을 밝혔다.

Dual Contouring을 이용해 비선형방정식의 계산에 적용하기 위해 제안한 방법은 변수의 개수와 식의 개수가 특수한 상태일때만 적용되도록 하였다.

1-manifold는 변수의 개수가 식의 개수보다 하나 더 많은 형태 이다. 1-manifold 일 때 해를 찾는 과정은 해가 포함된 초기 도메인을 주어진 크기까지 분할한다. 이후 분할된 하위 도메인의 중앙점을 계산하고 이점을 시작점으로 Newton-Raphson법을 이용해 실제 해를 계산하고 저장한다. 이때 저장된 실제 해와 그를 포함하는 도메인 정보를 이용해 전체 해의 위상학적이 구조를 결정하여 전체 해를 계산한다.

2-manifold는 변수의 개수가 식의 개수보다 두 개 더 많은 형태이다. 해들이 포함된 초기 도메인이 분할된 서브도메인이 주어진 크기에 만족하면 분할을 중단한다. 이후 분할된 하위 도메인의 중앙점을 계산하고 이점을 시작점으로 Newton-Raphson법을 이용해 실제 해를 계산하고 저장한다. 저장된 실제 해와 그를 포함하는 도메인 정보를 이용해 전체 해의 위상학적이 구조를 결정한다.

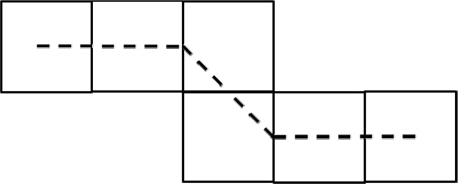
Fig. 1에서 실선으로 그려진 사각형은 해를 포함하는 영역을 나타내고 점선으로 표현된 선은 실제 해를 포함하는 도메인 간의 인접관계를 통해 얻어진 해를 가시화 한 것이다. 해를 포함하는 하위 도메인이 서로 인접하는 경우 도메인의 실제 해를 연결하는 선을 얻을 수 있다. Fig. 2에서 실선으로 표현된 정육면체는 해를 포함하는 영역을 나타내고 점선으로 표현된 삼각형은 Dual Contouring성질에 의해 얻어진 해를 연결한 것이다. 해를 포함하는 하위 도메인이 서로 인접하는 경우 도메인의 실제 해를 연결하는 면(삼각형)을 얻을 수 있다.

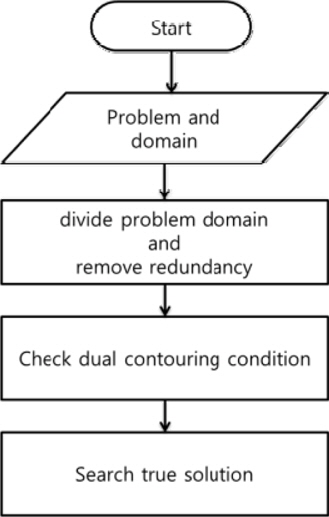
해의 유일성을 갖는 서브도메인을 확인하여 해의 유일성이 확인된 서브도메인에서만 해를 계산하므로 일반적인 수치기법에서 발생할 수 있는 에러는 발생하지 않는다. 또 수치기법의 경우 전체 해를 계산하기 위한 시작점으로 초기점을 요구하지만 Dual Contouring은 해를 포함 하고 있는 하위 도메인간의 위상학적인 관계를 판단하여 전체 해의 연결관계를 계산하기 때문에 초기점이 필요 없다. 자세한 사항은 Seong (2005)을 참고하기 바란다. 그리고 변수의 개수가 3보다 큰 문제(hyper space)에서도 1,2-manifold인 경우에는 동일한 개념으로 계산할 수 있는 장점이 있다. Fig. 3은 Dual Contouring의 과정을 정리한 순서도이다. 먼저, 곡면정보를 상징연산을 이용해 계산하고자 하는 식으로 변환한다. 그 결과 얻어진 Bezier곡면 형태의 식을 분할하고 분할된 Bezier곡면의 조정점을 검사하여 모든 조정점의 부호가 양이나 음이면 해를 포함하지 않는 영역으로 간주하고 제거한다. 이후 해를 포함하고 있는 영역들 간에 서로 이웃하는 정보를 이용해 해를 계산하는 영역을 확정하고 해를 계산한다. 그러나 컴퓨터의 실수연산 시에 발생하는 반올림에러(round error)에 대한 부분은 표현하지 않았다.

주어진 곡면이 B-spline인 경우 본 논문에서 사용하는 Bezier 곡면으로 분할하여 저장한다. 이후 Bezier 곡면의 상징연산을 적용하여 곡면을 곡률곡면으로 변환한다. 변환된 곡률곡면에 Dual Contouring 방법을 사용하여 가우스 곡률이 ‘0’으로 동일한 선을 추적한다. 가우스 곡률이 음인 부분의 면적과 양인 부분의 면적을 나누어 계산을 하려면 등곡률선을 기준으로 곡면을 분할하는 과정이 필요하다. 계산된 등곡률선의 형태는 곡면의 도메인상의 값으로 표현된다. 따라서 등곡률선으로 곡면의 도메인을 분할하고, 분할된 도메인을 저장한다. 분할된 도메인영역을 다시 여러개의 삼각형으로 분할한다. 이후 삼각형의 정점 정보를 이용하여 다시 곡면상에서 삼각형의 좌표를 계산하고 삼각형의 면적을 계산하고 계산된 결과를 합하여 분할된 도메인영역에 해당하는 곡면의 면적을 계산했다.

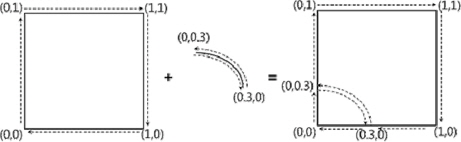
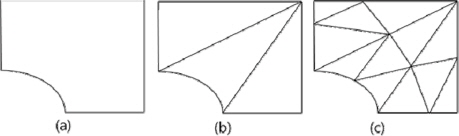
Fig. 4 는 곡면의 도메인을 분할하기 위해 Preusser (1986)가 제안한 방법의 개념을 정리한 것이다. 2차원 평면에서 면을 이루는 점이 화살표 방향으로 정렬되어 있을 때, 두 개의 방향으로 정렬된 점으로 이루어진 곡선이 주어지면 곡선을 이루는 점의 정렬된 방향 중 한쪽 방향으로 점을 저장하면 저장된 점에 의해 새로운 영역을 얻을 수 있다. 동일하게 곡선의 나머지 한쪽 방향을 따라 점을 저장하면 저장된 점에 의해 새로운 영역을 얻을 수 있다. Fig. 5는 분할된 도메인에서의 면적을 계산하기 위해서 분할된 도메인의 내부를 허용오차를 만족하는 크기의 삼각형으로 나누는 과정을 보이고 있다.

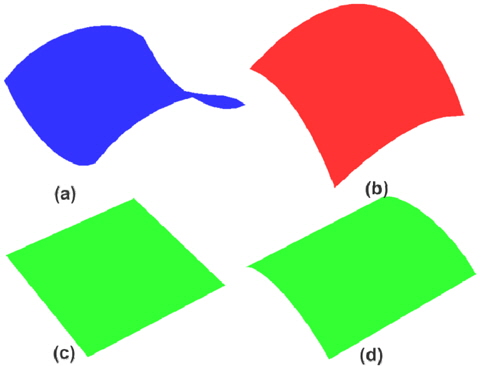
본 논문에서 제안한 방법의 검증을 위해 전형적인 곡면(Fig. 6)에 대한 곡률영역 계산했다. 그 다음 실제 조선 산업에 사용된 선체 외판 곡면 데이터를 활용해 곡률면적을 분석했다. 곡률 영역의 효율적인 비교를 위해 분할된 곡률면적을 다음과 같이 처리했다. 가우스 곡률이 양인 경우는 볼록형 곡면이며 이는 적색으로 표현하였고, ‘0’인 경우(실린더형과 평면형)는 녹색으로 표현 했다. 마지막으로 음인 경우는 안장형 곡면이며 이는 파랑색으로 표현하였다.

Fig. 7은 전형적인 곡면에 대한 곡률영역의 계산결과이다. 계산된 곡률에 해당하는 색을 이용해 음영(shading)모델로 처리했고, 곡면 전체에서 가우스 곡률이 음인 (a): 안장형 곡면에서는 곡면 전체가 청색으로 표현되었고, 곡면 전체에서 가우스 곡률이 양인 (b): 볼록형 곡면에서는 전부 적색으로 표현되었다. (c): 평면형 곡면과 (d): 실린더형 곡면은 곡면 전체에서 가우스 곡률이 ‘0’이므로 전부 녹색으로 표현됨을 확인할 수 있다. 아래는 다양한 곡면에 대한 곡률 영역의 계산 결과이다.

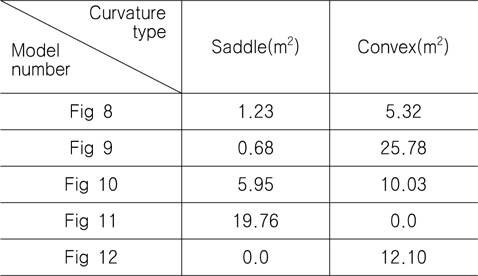
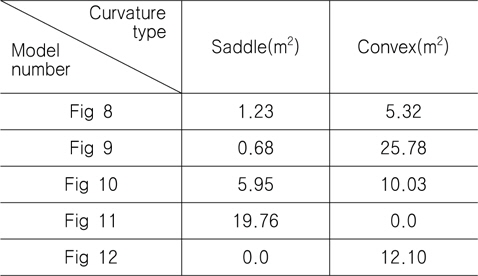
Fig. 8은 곡률이 음인 부분의 면적이 1.23m²이고 곡률이 양인 부분의 면적이 5.32m²이다. Fig. 9은 곡률이 음인 부분의 면적이 0.68m²이고 곡률이 양인 부분의 면적이 25.78m²이다. Fig. 10은 곡률이 음인 부분의 면적이 5.95m²이고 곡률이 양인 부분의 면적이 10.03m²이다. Fig. 11의 경우는 곡면 전체에서 가우스 곡률이 음이며 면적은 19.76m²이다. Fig. 12은 곡면 전체에서 가우스 곡률이 양이며 면적은 12.10m²이다. Table 1은 Fig. 8 ~ Fig. 12의 계산결과를 정리한 표이다.

본 논문에서 기존의 곡판 분류에 사용한 표준형상(점) 기반의 분류방법의 문제점을 지적했다. 그리고 대안으로 곡면의 등곡률선을 직접 계산하여 가우스 곡률이 양인 부분과 음인 부분을 구분하였다. 추적법은 초기 점이 주어진 경우 실제 해를 추적할 방향을 계산하고 계산된 방향으로 사용자가 정의한 크기(Step Size)만 큼 점진적으로 이동하여 전체 해를 계산하는 것이다. 따라서 추적법을 적용하기 전에 계산과정에 발생할 수 있는 예외 경우와 계산 시 사용할 Step Size를 충분히 고려해야 한다. 그러나 계산 전에 고려할 수 있는 예외상황과 Step Size를 벗어난 상황이 발생할 수 있다. 근사법의 경우 계산하고자 하는 해공간 전체를 최소자승법이나 다른 방법을 통해 하나의 곡면으로 재구성하여 재구성된 곡면과 평면간의 교차를 이용하여 원하는 해를 계산하게 된다. 해공간을 근사 하는 과정에서 발생할 수 있는 에러를 제어할 수 있는 방법이 존재하지 않는다. 따라서 정확한 값이 요구되는 작업에는 적합하지 않다.

앞의 방법들이 갖는 문제를 정리해 보면 예외상황에 대한 처리 문제와 수치적인 정확도로 요약된다. Dual Contouring은 해와 그 해를 포함하는 도메인간의 위상학적인 관계를 통해 추적법 사용 시 나타날 수 있는 예외상황에 대한 문제를 해결할 수 있다. 그리고 계산하고자 하는 값을 곡면의 대수적 연산을 적용해 변환함으로써 근사과정에서 나타날 수 있는 오차문제가 해결될 수 있다. 따라서 상징연산과 Dual Contouring 개념을 이용하여 등곡률선을 계산하게 되면 기존의 수치방법들보다 상대적으로 높은 신뢰성을 갖는 계산결과를 얻을 수 있다. 그리고 이를 통해 분할해상도에 관계없이 항상 동일한 분류 결과를 보이는 분류 방법에 대한 가능성을 생각해 볼 수 있다.

향후 연구로는 세 가지가 필요하다. 하나는 본 연구를 통해 정립된 방법을 이용한 곡판분류 방법의 개선이다. 기존연구는 분할 해상도에 의존적인 곡판의 분류결과를 보인다. 따라서 이와 관계 없이 항상 동일한 분류결과를 보이는 방법의 개발이 필요하다.

두 번째로는 본 연구를 통해 얻은 곡면의 영역정보를 이용해서 선체외판의 영역별 최적 가공정보에 대한 연구가 필요하다. 현재까지는 특정 곡면 전체에 선상가열이나 삼각가열 중 한 가지 가열 방법에만 해당하는 가공정보를 계산해 왔다. 이러한 방법은 곡면의 전체가 볼록형 이거나 안장형인 경우는 효율적이지만, 한곡면에 볼록형과 안장형이 섞여 있는 경우에는 현업에서는 두 가지 방법을 동시에 사용한다. 성형방법과 곡판의 영역정보가 완벽히 매칭이 되는 경우도 있지만 가공영역의 주변부 강성의 영향으로 실제 작업자가 생각하는 가열 패턴과 차이가 존재할 수 있다. 따라서 곡판의 영역정보를 이용해 가공방법을 결정하는 방법이 큰 의미를 갖지 않을 수도 있다. 그러나 최적화된 가공방법의 결정을 위한 하나의 대안으로써 고려할 필요성은 있다.

마지막으로 안장형 곡판을 가공하는 경우, 냉간가공과 열간가공을 순차적으로 실시하면서 발생하는 문제를 해결하는 방법에 대한 연구가 필요하다. 열간가공을 하는 과정에서 앞선 냉간가공에 의해 만들어진 형상이 유지되지 못하는 현상이 발생한다. 이는 열을 이용한 가공방법에 특성에 기인하여 발생하는 문제이고 이를 정량적으로 분석하는 일은 어려운 작업이다. 그러므로 단기간에 해결하기 매우 힘든 부분이다. 따라서 본 논문의 결과를 확장하는 향후 연구로 곡판을 구성하는 곡률의 영역에 대한 정량적 정보를 이용해 이 문제에 대한 새로운 접근을 시도하고자 한다.