최근 원유와 천연 가스의 수요가 꾸준하게 증가함에 따라 해양 플랜트에 대한 관심도 함께 증가하고 있다. 그 중에서도 FPSO는 심해에서 석유 및 천연 가스의 생산, 저장, 하역이 가능한 대표적인 해양 플랜트로서 이와 관련하여 많은 연구가 수행되고 있다 (Jung, et al., 2006).
FPSO는 멀고 깊은 바다에서 원유와 천연 가스의 생산부터 하역까지 다양한 작업을 수행하기 때문에 상부 구조(topside)에 많은 수의 모듈(module)과 장비(equipment)가 설치된다. 모듈은 유사한 기능을 가진 장비들을 그룹화한 것으로서 function group이라고도 현업에서 일컬어지며, 장비는 function sub-group으로 불려지기도 한다. 이들을 상부 구조에 배치할 때, 모듈의 수가 늘어날수록 검토해야 하는 배치 안의 개수는 기하 급수적으로 증가하며, 제한된 시간 내에 모든 경우를 고려하는 것은 현실적으로 매우 어렵다. 또한 해양 플랜트의 모듈 및 장비 배치는 육상 플랜트와 달리 제한된 공간에서 수행되기 때문에 다중 갑판(multi-deck) 설계, 자원의 흐름 및 사고 위험도 등 다양하게 고려할 사항들이 있다. 따라서 오래 전 PETRONAS (1990)는 해양 플랜트 상부 구조의 모듈 및 장비 배치의 방법론을 기술 표준(technical standard)을 통하여 제시한 바 있다. 이는 제한 공간내에 배치될 다양한 모듈의 성격을 정의함으로써 최적의 배치가 가능하도록 하는 일반적인 방법론으로서 PETRONAS는 Oil FPSO를 예제로 사용하였지만, 추후 FLNG의 모듈 배치에도 충분히 응용이 가능할 것으로 보인다.
본 연구에서는 기존의 배치 기술 표준에서 제시하는 고려 사항들을 반영하는 동시에 최적화 기법을 이용하여 짧은 시간 내에 많은 배치 안을 효과적으로 검토해 봄으로써 최적해에 가까운 결과를 얻을 가능성을 높이고자 하였다. 우선, 모듈과 장비의 최적 배치 문제를 각각 수학적 모델로 정식화하였으며, 유전 알고리즘(GA; Genetic Algorithm) 기반의 최적화 기법을 이용하여 FPSO 상부 구조의 배치를 수행하였다.
PETRONAS (1990)는 해양 플랜트의 상부 구조 전 단계에 걸친 모듈 및 장비 배치에 대한 기술 표준을 제시하였다. 제안한 방법론의 기본 개념으로서 계층적 접근(hierarchical approach)을 통하여 배치를 수행하였다. 즉, 상부 구조에 배치될 장비들을 유사한 기능별로 그룹화한 뒤에 순차적으로 단계별 배치를 진행하였다. 통계 자료를 기반으로 하여 사고 위험도를 고려하였으며, 공정상 자원의 흐름과 검사관의 이동량을 반영하였다. 배치 모델이 아닌 방법론에 대한 기술 표준으로서 전산 기법을 활용하여 최적화를 수행한 내용은 없으며, 상대적인 위치를 도식화한 다이어그램을 토대로 모듈과 장비의 위치를 할당하는 방식으로 배치를 결정하였다.
Patsiatzis and Papageorgiou (2002)는 다양한 화학 공정 플랜트에 대해 장비의 최적 다층 배치를 수행하였다. 설계 변수로서 층의 개수와 면적, 각 장비의 할당된 층, 위치, 설치 방향을 정의하였으며, 목적 함수로는 배치 비용(layout cost), 즉 층의 면적에 따른 비용, 층의 개수에 따른 비용, 장비들 간의 파이프 설치 및 펌프 사용 비용을 더한 값으로 정의하였다. 이를 통해 정식화한 수학적 모델을 MILP(Mixed Integer Linear Programming)로 풀어 장비의 최적 배치를 결정하였다.
Ku, et al. (2012)은 안전성을 고려하여 다중 갑판인 LNG FPSO의 액화 공정을 위한 장비의 최적 배치를 수행하였다. 설계 변수는 Patsiatzis and Papageorgiou (2002)에서 정의한 변수에서 층의 개수를 고정하여 제외하였고, Penteado and Ciric (1996)과 같이 제약 조건에 장비 사이의 최소 거리를 규정함으로써 안전성을 고려하였다. 목적 함수로는 층의 면적에 따른 비용과 장비들 간의 파이프 설치 비용을 더한 값을 배치 비용으로 정의하였다. 이 때 갑판간의 높이 보다 큰 열교환기(heat exchanger)와 같이 다수의 갑판을 관통하는 장비를 고려한 것이 특징적이다.
PETRONAS (1990)의 해양 플랜트 상부 구조의 배치 방법론에 따르면 장비 배치의 단계에서 장비가 배치될 공간의 제약이 있는 경우, 탄화수소 파이프가 유정(wellhead) 구역을 관통하는 경우, 또는 공정 흐름의 논리에 비추어 더 선호되는 배치 안이 존재하는 경우에 어떤 장비는 기존에 그룹화된 모듈의 범위를 벗어나 재배치(reallocation)가 이루어진다. 따라서 해양 플랜트 상부 구조의 배치를 수행함에 있어서 Patsiatzis and Papageorgiou (2002)나 Ku, et al. (2012)과 같이 장비 배치의 대상을 단일 모듈에 한정하면 실제적인 배치 결과를 얻는 데에 한계가 있다.
따라서 본 연구에서는 해양 플랜트 배치 문제를 모듈 및 장비 두 단계 모두에 대하여 배치를 수행함으로써 계층간의 동시성을 고려하였다. 우선, 모듈 배치의 경우 PETRONAS (1990)와 동일하게 사고 위험도 및 공정상 자원의 흐름과 검사관의 이동량을 고려하였다. 장비 배치의 경우 Patsiatzis and Papageorgiou (2002)와 Ku, et al. (2012)을 참조하여 각 장비의 할당된 층, 위치, 설치 방향을 설계 변수로 배치 비용을 목적 함수로 정의하였다. 또한 장비 사이의 최소 거리를 규정함으로써 안전성을 고려하였다. 앞선 두 연구에서 MILP를 토대로 한 것과 달리 유전 알고리즘을 기반으로 하여 수학적 최적화 모델을 정식화하였기 때문에 설계 변수와 제약 조건의 개수를 크게 줄였다.
위 사항들을 정리하면 Table 1과 같다.

Comparison of the layout model for process modules and equipment between authors’ study and others
앞서 설명하였듯이, FPSO 상부 구조에는 다수의 모듈 또는 function group이 배치되며, 하나의 모듈 내에는 다수의 장비 또는 function sub-group이 배치된다. 따라서 FPSO 상부 구조의 배치 문제는 모듈의 배치 문제와 모듈 내 장비 배치 문제로 구성된다. 본 연구에서는 이들 각각을 최적화 문제로 정식화한 후 순차적으로 풀어 FPSO 상부 구조에 대한 최적 배치를 도출하고자 하였다.
Fig. 1은 본 연구에서 제안한 FPSO 상부 구조의 최적 배치 모델을 나타낸 것이다. Fig. 1에 나타나 있듯이, 모듈의 최적 배치 문제를 수학적으로 정식화한 후(Fig. 1의 ② 참조), 이를 유전 알고리즘을 이용하여 풀어 FPSO 상부 구조 모듈의 최적 배치를 도출하였고(Fig. 1의 ③ 참조), 이후 모듈 배치의 결과를 토대로 각 모듈 내 장비들의 최적 배치 문제를 수학적으로 정식화한 후(Fig. 1의 ⑤ 참조), 이를 유전 알고리즘으로 풀어 모듈 내 장비의 최적 배치를 도출하였다(Fig. 1의 ⑥ 참조).
3장에서는 모듈의 최적 배치 문제를 설명하며, 4장에서는 모듈 내 장비의 최적 다층 배치 문제를 설명하기로 한다.
본 연구에서 FPSO 상부 구조의 모듈 배치 문제는 각 모듈이 배치될 최적 위치를 결정하는 것이다. 목적 함수는 전체 모듈의 배치 비용(layout cost)과 모듈 전체의 무게 중심과 중심선(center line)과의 거리를 최소화하는 것이다. FPSO 모듈 배치시 주어지는 입력 정보는 다음과 같다.
(1) Zone 정보
- 전체 zone의 수(길이 방향, 폭 방향 zone의 수) - 각 zone 번호(ID) - 각 zone의 길이 및 폭 - 각 zone의 중심 좌표
여기서, zone은 모듈이 배치되는 FPSO 상부 구조의 가상 공간을 말한다.
(2) 모듈 정보
- 전체 모듈의 수 - 각 모듈 번호(ID) - 각 모듈의 중량 - 모듈간의 배치 비용 계수(layout cost factor)
(3) 기타 정보
- FPSO 상부 구조의 크기(길이 및 폭)
2.2.1 모듈 배치의 표현 방법
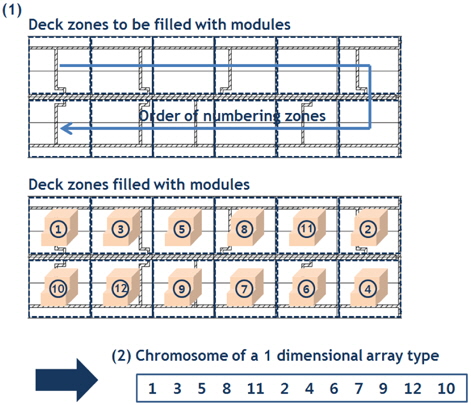
모듈의 배치, 즉 각 모듈이 배치될 위치는 유전 알고리즘의 암호화(encoding) 과정에 의해 염색체(chromosome)로 표현될 수 있다. 그리고 그 염색체는 해독(decoding) 과정에 의해 다시 모듈의 배치로 표현될 수 있다. 본 연구에서는 각 모듈의 배치 결과를 포함하는 1차원 배열 형태의 염색체를 이용하였다. 즉, 염색체 내 유전자(gene)의 개수는 배치의 대상이 될 모듈의 개수와 같다. Fig. 2는 모듈 배치 결과와 이에 대한 염색체 표현의 예를 나타낸다. Fig. 2의 (1)은 FPSO 상부 구조에 모듈이 배치될 수 있는 공간(zone)을 정의하고, 각 zone에 모듈이 배치된 모습을 나타낸다. Fig. 2의 (2)는 이를 염색체로 표현한 것이다. 즉,
2.2.2 모듈의 배치 비용 계산
공장 배치, 공장 내의 장비 배치, 건물 내의 사무실 배치 등과 같은 다양한 분야의 공간 배치 문제(FLP; Facility Layout Problem)에서는 facility의 수, facility간 재화(material)의 유동량 등이 주어졌을 때, facility간 재화의 운반 비용의 합을 최소화하는 것을 목적 함수로 한다 (Kado, 1995; Liggett, 2000).
FPSO의 모듈 배치에서 재화의 유동량 최소라 함은 공정 상의 재화와 작업자(staff)의 이동량을 최소화하는 것으로 생각할 수 있다 (PETRONAS, 1990). 한편, FPSO 상부 구조의 모듈 배치 시 사고 위험성이 최소화되도록 하는 것 또한 중요하다. 따라서 본 연구에서는 모듈간의 인접 관계를 나타낼 특성을 모듈간 적대성 및 친밀성으로 정의하였고 이를 토대로
이때, 모듈간 적대성은 화재나 폭발이 방벽에 의해 보호되지 않을 때 모듈이 임의의 다른 모듈 근처에 안전하게 위치할 수 없는 특성을 말한다. 이 같은 특성은 모듈의 유발성 행동 특성(active behavior characteristics, 주요한 사고를 발생시킬 가능성을 나타내는 특성)과 반응성 행동 특성(reactive behavior characteristics, 다른 모듈에서 발생한 사고를 악화시키는 경향을 나타내는 특성)으로부터 구할 수 있다.
그리고 모듈간 친밀성은 모듈이 다른 어떤 모듈 근처에 위치할 때 유리한 특성을 말한다. FPSO 모듈 배치의 경우 두 가지 관점에서 친밀성을 살펴볼 수 있다. 첫째는 가장 기초적인 공정 논리에 따른 것(engineering affinities)이며, 둘째는 작업자의 플랫폼 주위 이동 거리를 최소화하는 것(manning affinities)이다.
본 연구에서는 앞서 설명한 모듈간 적대성 및 친밀성의 중요도를 동일하게 가정하여 모듈간 배치 비용 계수 행렬을 구성하였다(Jeong, et al., 2013). 행렬의 각 요소는
[Table 2] Example of closeness factors matrix for full function groups

Example of closeness factors matrix for full function groups
Table 2에 나타난 행렬의 원소의 범위는 0에서 8이며, 이 원소에 해당하는 모듈간 배치 비용 계수(
식 (2)에서 전체 배치 비용의 합을 계산할 때, 식 (2)에 포함되어 있는 두 모듈간의 거리(
2.2.3 모듈의 전체 무게 중심 계산
일반적으로 FPSO의 선체는 중심선을 기준으로 좌현과 우현이 대칭이라고 볼 수 있다. 상부 구조에 모듈이 배치됨에 따라 무게 중심이 중심선에서 벗어나게 되면 선체에 횡경사(heel) 또는 종경사(trim)가 발생한다. 따라서 선체와의 연관성(interface)을 고려했을 때, 모듈의 전체 무게 중심 위치가 중심선에 가까울수록 조선 공학적으로 좋은 배치라 할 수 있을 것이다. 다만, 모듈의 길이 방향 무게 중심의 위치는 선체의 무게 중심 위치와 연관되기 때문에 본 연구에서는 문제를 간략히 하기 위해 선체와 관련되어 있는 모듈의 길이 방향 무게 중심의 위치는 고려하지 않고 폭 방향 무게 중심의 위치만 고려하여, 모듈 전체의 무게 중심의 위치가 중심선에 가까운 배치를 좋은 배치라고 가정하였다. 본 연구에서 모듈 전체의 폭 방향 무게 중심 위치는 식 (3)과 같이 간단히 계산하였다.
본 연구에서는 FPSO 모듈 배치 문제의 수학적 정식화를 위해 다음과 같은 변수와 기호를 사용하였다.
N : zone 및 모듈의 총 수 qi,j : i번째 모듈과 j번째 모듈간 배치 비용 계수 di,j : i번째 모듈과 j 번째 모듈간 거리 wi: i 번째 모듈의 중량 xi: i 번째 모듈의 길이(x축) 방향 중심 좌표 yi: i번째 모듈의 폭(x 축) 방향 중심 좌표
이제 2.1절에서 서술된 FPSO 모듈 배치 문제를 수학적으로 정식화하면 다음과 같다.
and
식 (2)는 모듈의 총 배치 비용을 의미하고, 식 (3)은 전체 모듈의 폭 방향 무게 중심과 중심선과의 거리를 의미한다. 즉, 위의 두 목적 함수를 최소화하는 최적화 문제가 된다. 이때 식 (2), (3)으로 표현된 문제는 두 개의 목적 함수(
본 연구에서 모듈 내 장비 배치 문제는 각 장비가 배치될 최적 위치를 결정하는 것이다. 장비의 다층 배치 문제는 2장의 모듈 배치 문제와 달리 비동등 면적 배치 문제(unequal area facility layout problem)로서 장비 배치 시 주어지는 입력 정보는 다음과 같다.
(1) 모듈 정보
- 모듈의 크기(길이 및 폭) - 모듈의 갑판(층) 수
(2) 장비 정보
- 전체 장비의 수 - 각 장비의 치수(가로(li), 세로(bi)) - 장비간 파이프 연결 비용 계수 - 장비간 파이프 내 물질의 수직 이동을 위한 펌프 사용 비용 계수 - 장비간 파이프 내 물질의 수평 이동을 위한 펌프 사용 비용 계수
본 연구에서는 FPSO 모듈 배치 문제의 수학적 정식화를 위해 다음과 같은 변수와 기호를 사용하였다.
i , j : 장비 번호 αi, βi: 장비 i 의 주요 치수 H : 갑판 높이 fi,j : 장비간 유동량이 있다면 1, 그렇지 않다면 0으로 함 : 장비 i 와 장비 j 를 파이프로 연결할 때 필요한 비용 계수 : 장비 i 와 장비 j사이의 파이프 내 물질의 수직 이동을 위한 펌프 사용 비용 계수 : 장비 i 와 장비 j사이의 파이프 내 물질의 수평 이동을 위한 펌프 사용 비용 계수
다음 절에서는 장비의 최적 다층 배치 문제의 설계 변수, 제약 조건, 목적 함수를 상세히 설명하였다.
3.2.1 설계 변수(design variables)
장비의 최적 다층 배치 문제의 수학적 정식화를 위해 다음과 같은 설계 변수들을 선정하였다 (Patsiatzis & Papageorgiou, 2002).
(1) 정수 변수(integer variables)
NF: 갑판(층) 수 Fi: 장비 i가 배치될 갑판(층) 번호
(2) 이진 변수(binary variables)
Oi: 장비의 길이 li가 αi와 같다면(즉, αi가 x축에 평행 할 경우) 1, 그렇지 않다면 0으로 함
(3) 연속 변수(continuous variables)
li: i번째 장비의 길이 bi: i번째 장비의 폭 xi, yi: i번째 장비의 중심 좌표 Xij : 장비 i 와 장비 j의 중심의 길이(x축) 방향 상대적 거리, │xi – xj│ Yij : 장비 i와 장비 j의 중심의 폭(y축) 방향 상대적 거리, │yi – yj│ Zij : 장비 i와 장비 i의 중심의 높이(z축) 방향 상대적 거리, │zi – zj│ TDij : i번째 장비와 j번째 장비간 총 직교 거리(total rectilinear distance) Xmax, Ymax: 모듈의 길이, 모듈의 폭
3.2.2 제약 조건(constraints)
장비의 최적 다층 배치 문제의 제약 조건들로는 다음의 것들을 고려하였다.
(1) 갑판 배치 제약 조건(deck layout constraints)
각 장비는 배치된 갑판 면적을 벗어날 수 없다. 그러므로 원점 좌표에 대해 아래의 식 (4)∼(7)의 부등호 제약 조건을 만족해야 한다. Fig. 4는 축 방향의 갑판 배치 제약 조건이 어떻게 결정되었는지 나타낸다. 큰 직사각형은 장비가 배치될 갑판을 의미한다. 작은 직사각형으로 나타낸 장비는 축 방향을 기준으로 부터의 위치 안에서 배치될 수 있고, 이를 식으로 나타내면 식 (4), (6)과 같다.
또한 장비와 갑판을 이루는 변들 사이의 최소 거리를 반영하고자 한다면 식 (4)∼(7)은 식 (8)∼(11)의 부등호 제약 조건으로 대체할 수 있다.
여기서,
(2) 장비 설치 방향 제약 조건(equipment orientation constraints)
장비의 길이와 폭은 장비의 설치 방향에 따라 결정된다. 따라서 본 제약 조건은 설치 방향을 나타내는 이진 변수 를 이용하여 다음과 같이 등호 제약 조건으로 나타낼 수 있다.
(3) 겹침 방지 제약 조건(non-overlapping constraints)
직사각형 모양의 장비
또한 장비간의 최소 거리를 반영하고자 한다면 식 (16)과 (17)의 부등호 제약 조건으로 대체할 수 있다.
여기서,
이 부등호 제약 조건은 충분히 큰 수
(4) 거리 제약 조건(distance constraints)
장비
3.2.3 목적 함수(objective function)
본 연구에서 장비의 최적 배치 문제는 장비를 배치하는데 필요한 총 배치 비용(layout cost)을 최소화하는 것을 목적 함수로 가정하였다. 장비를 배치하는데 소요되는 비용에는 장비 사이의 총 파이프 길이에 대한 비용, 파이프 내에서 위로 흐르는 물질을 위한 펌프 사용 비용, 파이프 내에서 수평으로 흐르는 물질을 위한 펌프 사용 비용이 있으며 (Patsiatzis & Papageorgiou, 2002), 아래와 같이 이들의 모든 합을 목적 함수로 가정하였다.
3.2.4 장비 다층 배치 문제의 정식화
이 절에서는 앞서 4.2.1절에서 4.2.3절까지 소개한 설계 변수, 제약 조건, 목적 함수를 수학적으로 정식화한다. 이때 유전 알고리즘은 근본적으로 제약 조건이 없는 비제약 최적화 문제를 해결하기 위해 사용되므로 4.2.2절에 표현되는 제약 조건이 있는 최적화 문제를 penalty function 방법을 이용하여 제약 조건이 없는 비제약 최적화 문제로 변환하면 식 (21)과 같다.
여기서,
3.3.1 장비의 최적 배치 알고리즘
Patsiatzis and Papageorgiou (2002)는 다양한 처리 공장의 설비 배치 문제를 MILP 문제로 정식화하여 풀었다. 또한 Ku, et al. (2012)은 Patsiatzis and Papageorgiou (2002)의 연구를 참조하여 LNG FPSO의 액화 공정 내의 장비 배치 문제를 MILP 문제에 적용하였다. 하지만 MILP 문제는 변수의 개수와 제약 조건이 비교적 많기 때문에 낮은 수렴성을 보인다. 따라서 본 연구에서는 기존의 장비 배치 연구를 참조하여 유전 알고리즘을 기반으로 수학적으로 정식화하였다. 그리고 이를 컴퓨터 프로그램으로 구현하였다. 유전 알고리즘의 일반적인 흐름도는 Fig. 2에 나타내었다. 이때 적합성 값의 계산(Fig. 2의 ② 참조)은 장비 배치 문제의 목적 함수인 식 (20)으로부터 구한다.
3.3.2 장비 배치의 표현 방법
장비의 배치, 즉 각 장비가 놓일 위치는 유전 알고리즘의 암호화 과정에 의해 염색체로 표현될 수 있다. 그리고 그 염색체는 해독 과정에 의해 다시 장비의 배치로 표현될 수 있다. 본 연구에서는 Fig. 6과 같이 각 장비의 배치 결과를, 4개의 segment를 갖는 1차원 배열 형태의 염색체로 표현하는 방법을 제안하였다. Fig. 6에서 첫 번째 segment는 장비들의 방향을 나타내는 orientation 변수, 두 번째 segment는 장비들이 설치되는 층수, 세 번째 segment는 장비들의
본 연구에서는 앞서 서술한 것과 같은 모듈의 최적 배치 문제와 장비의 최적 배치 문제를 풀기 위해 각각 유전 알고리즘을 기반으로 한 최적화 모델을 컴퓨터 프로그램으로 구현하였고, 본장에서는 이를 간단한 FPSO 상부 구조의 배치 문제(모듈 배치 문제, 장비 배치 문제)에 적용한 결과를 소개한다.
본 연구에서 제안한 방법의 효용성을 검증하기 위해, 이를 ConocoPhillips의 Belanak FPSO 상부 구조의 모듈 배치 예제에 적용하였고, 그 결과를 비교해 보았다.
본 예제에서 사용한 목적 함수는 2.2절에서 제안한 모듈간 배치 비용을 최소화하는 것(식 (1), 작을수록 좋음)과 모듈 전체의 무게 중심과 상부 구조의 중심선과의 거리를 최소화하는 것(식 (2), 작을수록 좋음)이다. 이때, 모듈 배치 비용을 정의하는 것은 2.2절에서 설명하였듯이 FPSO의 공정 논리를 바탕으로 한다. 본 절에서 다룬 해양 플랜트 상부 구조의 공정을 Fig. 7에 간략히 나타내었다.
Fig. 7에 나타나 있듯이, 상부 구조에 공급된 원유는 oil 성분과 gas 성분으로의 2상 분리 과정을 거친 후 반복적인 압축과 수분 제거 과정을 거쳐 석유 제품으로 생산된다.
이같이 정식화된 다목적 최적화 문제를 지배 순위 기반의 적합도 할당 방법을 적용한 유전 알고리즘을 구현하여 해결하였다.
Belanak FPSO의 주요 치수는 Table 3에 나타내었고, 배치의 대상이 된 모듈은 Table 4에 나타내었다.
[Table 3] Principal dimensions of the Belanak FPSO

Principal dimensions of the Belanak FPSO
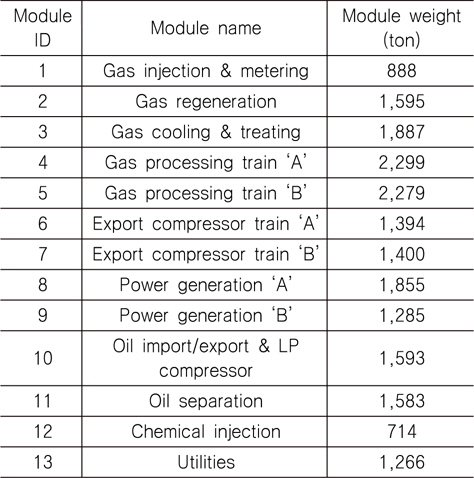
[Table 4] Modules on FPSO topsides to be considered in this study

Modules on FPSO topsides to be considered in this study
우선 기존의 배치 기준의 고려 사항들만을 목적물 함수로 하는 단일 목적 최적화를 수행한 결과를 Fig. 8과 같이 도식화 하였고, 목적 함수 값을 기존의 배치안과 비교한 결과를 Table 5에 나타내었다.

Comparison of the performance results of the existing layout and the optimal layout by the proposed method
이때, Fig. 8의 A, B, C zone은 각각 flare boom, workshop/warehouse, laydown area이 배치될 위치로 제약하였다. Table 5에 나타나 있듯이, 본 연구에 의한 결과(식 (1) 참조)와 실제 FPSO 상부 구조의 배치 결과가 유사함을 할 수 있으며, 약간의 오차는 본 연구에서 정의한 근접도 계수와 실제 FPSO 상부 구조 배치 시에 고려한 특성치의 차이에서 온 오차라고 예상된다.
다음은 같은 예제에 대하여 목적 함수를 추가해 다목적 최적화를 수행하였다. 즉, 선체와의 연관성을 고려할 수 있도록 모듈 전체의 무게 중심과 상부 구조의 중심선과의 거리를 최소화하는 목적 함수(식 (2) 참조)를 추가하였다. 모집단(population)의 개체 수와 최적화의 종료 조건인 세대(generation) 수를 다양하게 바꿔가며 제안된 방법을 반복 실행한 결과, Fig. 9와 같이 모집단 개체들이 수렴하는 것을 확인하였다.
Fig. 9에 나타난 그래프의 가로축은 모듈 전체의 무게 중심과 상부 구조의 중심선과의 거리를 최소화하는 목적 함수 값을 나타내고(식 (2) 참조), 세로축은 모듈 전체의 근접도 함수 값을 나타낸다(식 (1) 참조). 두 개의 목적 함수 모두 작을수록 좋은 해이기 때문에 그래프의 원점에 가까울수록 더 좋은 해라고 할 수 있다. Fig. 9의 ⃝는 10번째 세대에서 개체의 분포를 나타내고, ∗는 300번째 세대에서 개체의 분포를 나타낸다. 즉 세대를 거듭할수록 개체들이 원점에 가까워지며 파레토 프론트(Pareto front)를 형성하는 것을 알 수 있다. 충분한 수의 세대를 거친 후에 얻은 몇 개의 파레토 최적해를 Table 6에 정리하였다.
[Table 6] Pareto points of the multi-objective optimization problem in the example

Pareto points of the multi-objective optimization problem in the example
Table 6에 나타나 있듯이, 임의의 두 점을 비교하였을 때 어떤 한 점도 다른 한 점보다 두 목적 함수 측면에서 모두 더 작은(좋은) 값을 가지는 것은 없다. 즉, 서로 지배하는 해가 없기 때문에 어떤 것도 최적해의 가능성이 있는 파레토 최적해임을 확인할 수 있다. 즉, 설계자는 설계의 관점에 따라 최적해를 선택할 수 있다.
한편, 3장에서 수학적으로 정식화한 장비의 다층 배치 문제를 간단한 장비 배치 예제에 적용해 보았다. Table 7은 하나의 모듈내에 배치되는 장비의 종류와 크기를 나타내고, Table 8은 장비간 연결 관계 및 펌프 사용 비용 계수를 나타낸다.
[Table 7] Dimensions of each equipment in this example

Dimensions of each equipment in this example
[Table 8] Connection and pumping costs between equipment in this example

Connection and pumping costs between equipment in this example
본 연구에서는 이 문제를 유전 알고리즘을 이용하여 풀었으며, 그 결과는 Table 9에 나타나 있고, Fig. 10은 그 결과를 그림으로 도식화한 것이다.
[Table 9] Optimal layout by the proposed method of this example

Optimal layout by the proposed method of this example
본 연구에서는 대표적 부유식 해양 플랜트인 FPSO 상부 구조의 모듈 배치 및 모듈 내 장비의 다층 배치를 수행하였다. 우선 모듈 배치를 위해 최적 배치 알고리즘을 제안하였고, 이를 기반으로 한 프로그램을 개발하였다. 이를 위해, 먼저 모듈간 재화의 유동량과 모듈의 폭 방향 무게 중심의 위치를 고려하여 FPSO 모듈 배치 문제를 다목적 최적화 문제로 정식화하였고, 이를 해결하기 위한 유전 알고리즘 기반의 최적화 알고리즘을 개발하였다. 그리고 나서 모듈 배치 후 수행되어야 하는 모듈 내의 장비 배치 문제를 수학적 최적화 문제로 정식화하였고, 이를 해결하기 위한 유전 알고리즘 기반의 최적화 알고리즘을 개발하였다. 마지막으로 본 연구에서 제안된 알고리즘 및 개발된 프로그램의 효율성과 효용성을 검증하기 위해, 이를 실제 FPSO의 상부 구조 문제에 적용하였고 그 결과를 검토하였다. 그 결과, 본 연구에서 제안된 방법을 이용할 경우, 모듈의 배치 비용과 모듈의 무게 중심과 중심선과의 거리를 감소시킬 수 있는 개선된 배치 안을 도출할 수 있음을 확인하였다. 또한 모듈 내의 장비 배치 문제 역시 기존의 MILP 알고리즘이 아닌 유전 알고리즘으로 수학적 모델을 정식화함으로써 설계 변수와 제약 조건의 개수를 줄이고 효과적으로 문제를 해결할 수 있음을 알 수 있었다. 따라서 제안된 방법을 실제 FPSO 상부 구조의 배치 문제에 적용한다면 충분히 좋은 배치 결과를 얻을 수 있으리라 예상된다.
현재 본 연구에서 모듈 배치 문제와 모듈 내 장비 배치 문제는 독립적으로 수행되고 있는데 이를 연동 및 통합하여 풀 수 있는 환경을 개발할 예정이며(즉, 모듈 배치와 장비 배치간의 상호 영향을 고려), 보다 실제적인 예제에 제안된 방법을 적용해 봄으로써 그 효용성을 더욱 제고시킬 예정이다.