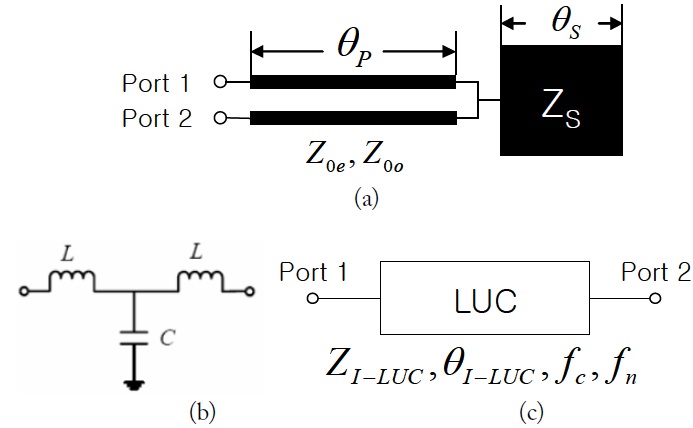
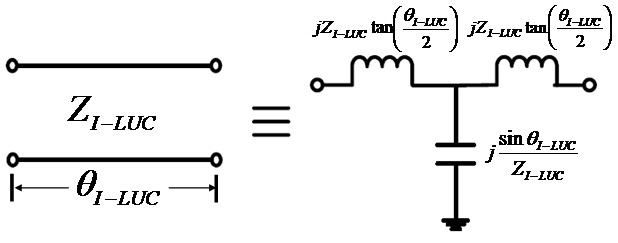
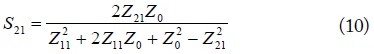Size and Harmonic Reduced Wilkinson Balun Using Parallel Coupled Line with Open Stub

Lee Won-Kyun; Hwang Hee-Yong

doi:10.5515/JKIEES.2014.14.4.387

OA학술지
Journal of electromagnetic engineering and science

Size and Harmonic Reduced Wilkinson Balun Using Parallel Coupled Line with Open Stub

DOI : 10.5515/JKIEES.2014.14.4.387
Author: Lee Won-Kyun, Hwang Hee-Yong
Organization: Department of Electrical and Electronic Engineering, Kangwon National University, Chuncheon, Korea.; Department of Electrical and Electronic Engineering, Kangwon National University, Chuncheon, Korea.
Publish: Journal of electromagnetic engineering and science Volume 14, Issue4, p387~392, Dec 2014

ABSTRACT

In this paper, a size-reduced Wilkinson balun with wide harmonic-suppressed band is presented. An accurate analysis of the parallel coupled line with an open stub (PCL-OS) is carried out. The PCL-OS structure shows excellent low pass filter and harmonicsuppression characteristics, which is useful for designing a low pass filter unit cell (LUC) with a reduced size. The designed Wilkinson balun at a 2.45 GHz center frequency not only shows an excellent harmonic suppression including the 5th harmonics up to 14 GHz over 15 dB, but it also has an area reduced to 48% of the conventional one.

KEYWORD

Harmonic Suppression , Low Pass Filter Unit Cell (LUC) , Parallel Coupled Line with an Open Stub (PCL-OS) , Wilkinson Size Reduction , Balun

본문

Collapse all

I. INTRODUCTION

The parallel coupled line with an open stub (PCL-OS) in Fig. 1(a) has been reported and widely adopted as a building block or low pass filter unit cell (LUC) in designing a compact low pass filter [1], compact wideband bandstop filters [2,3], an harmonic and size reduced ring hybrid [4], and a compact and harmonic suppressed Wilkinson power divider [5]. The PCL-OS demonstrates excellent performances, including its low pass filter with wideband rejection characteristics and sharp skirt response as well as its structural compactness. The equivalent T-network and equivalent LUC block are represented in Fig. 1(b) and (c). The analysis of this PCL-OS was also attempted in [2,4,5].

[Fig. 1.] (a) The structure of the parallel coupled line with an open stub (PCL-OS). (b) The equivalent T-network and (c) equivalent low pass filter unit cell (LUC) block.

However the derived analytical equations for the PCL-OS are approximated as an undefined floating port of the coupled line, which is connected to the open stub, is used as if a defined port in the analysis of the serially connected two-port networks in Fig. 2 of [2], Fig. 3 of [4], and Fig. 1 of [5]. The equivalent capacitance C in Fig. 1 was treated as a simple summation of the equivalent capacitance of the parallel coupled line (CP in [2,4,5]) and the equivalent capacitance of the open stub (CS). An even-odd mode analysis of the structure is also reported [3], which is limited in the transmission zeros with a quarter-wavelength for a bandstop filter design. When we design a microwave component that contains the PCL-OS or LUC using the previous equivalent equations, we have to perform repetitive iteration processes to obtain exact or desired characteristics.

[Fig. 2.] (a) The microstrip version of [6, 7] and (b) the proposed microstrip Wilkinson balun.

[Fig. 3.] (a) Parallel coupled line. (b) Equivalent circuit for Fig. 1(a).

Meanwhile, a simple coplanar waveguide (CPW) balun having the structure of a Wilkinson divider has been recently proposed [6–8]. The balun consists of two 3λ/4 and λ/4 transmission lines with a λ/2 line with Z₀ and a resistor with 2Z₀. Hence, it has serious drawbacks in its size and unwanted harmonics for low frequency applications. The microstrip version of the Wilkinson balun is shown in Fig. 2(a).

In this research, we first derived the exact design equations for the LUC by applying the full even-odd mode analysis to the whole PCL-OS structure.

Second, to demonstrate the validity of the analysis we applied the design equations for the LUC to designing a size and harmonic reduced microstrip Wilkinson balun as shown in Fig. 2(b).

II. ANALYSIS OF PCL-OS

To analyze the PCL-OS structure we assumed that the structure is lossless and the discontinuity effect between the parallel coupled line and the open stub is negligible.

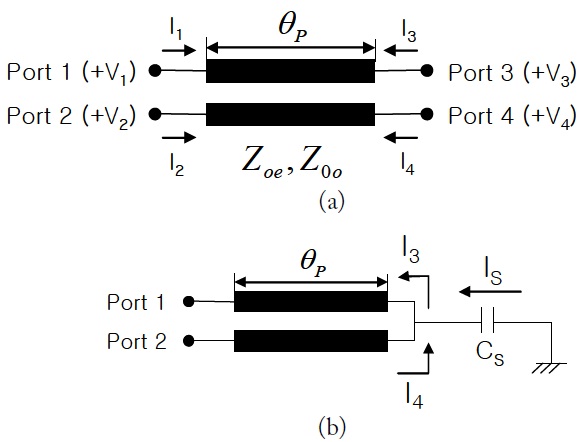
The characteristics of a parallel coupled line as shown in Fig. 3(a) can be expressed as an impedance matrix as follows [9],

where θ_P, Z_{0_e}, and Z_{0_o} are the electrical length, even- and oddmode impedances of the parallel coupled line, respectively.

The open-stub section is modeled as an equivalent capacitor, C_s as shown in Fig. 3(b).

where ω is the angular frequency, and θ_s is the electrical length of the open-stub.

The relations between the node voltages and the branch currents around the connection point in Fig. 3(b) are given as (3a) and (3b) by Kirchhoff’s law.

Using (3a)–(3b) and the well-known port reduction procedure the four-port impedance matrix, (1a)–(1d), can be converted into a two-port impedance matrix, (4a)–(4b).

where,

To design the three-stage low pass filter in Fig. 1(b) with a given specification of ripple and cutoff frequency f_c, we can determine the L and C values from the standard low pass filter design procedure [9]. The impedance matrix of T-type low pass filter can be derived as

where ω₀ is the center angular frequency of the LUC’s calculation and design.

By equating (4) to (5), we can calculate the exact equivalent capacitance, C_S, for the PCL-OS with the characteristics of the low pass prototype filter, as follows.

where D = ω₀CZ_{0_e}, E = ω₀CZ_{0_o}

Now, we can decide the other structural parameters for the PCL-OS in Fig. 1(a), which performs the response for the desired low pass filter in Fig. 1(b), using the equivalent parameters for coupled line part of the PCL-OS from [1] and [9], as follows.

where Z_I and βℓ are the image parameters of the parallel coupled line.

Meanwhile, the designed PCL-OS with low pass filter characteristics can be used to design various devices that have λ/4 transmission-line blocks or λ/4-LUCs. The λ/4-LUC is defined as an equivalent λ/4 line consisting of an LUC and two short transmission lines.

The image parameters of the LUC in Fig. 1(c) can be obtained as (8), equating the T-network in Fig. 1(b) with the T-type equivalent circuit for a transmission line in Fig. 4.

[Fig. 4.] A transmission line and its T-type equivalent circuit.

where θ_I-LUC is the image electrical length and Z_I-LUC is the image impedance. From (2) and (4), the impedance matrix of the PCL-OS or the LUC can be derived as (9).

where

To compare the exactness of derived (4a)–(4b) with those previously reported, (1) of [2] or Z_T of [5], arbitrary parameter values for a PCL-OS in Table 1 are used to calculate and simulate the Z-parameters, and the graphical results are depicted in Fig. 5. Here, the real parts of the impedance parameters are zero for all frequencies and hence do not appear in the figure. The Z-parameter values calculated by the ADS simulator are exactly the same as those by (4a)–(4b) above, while the equations of [2] and [5] provide approximated values.

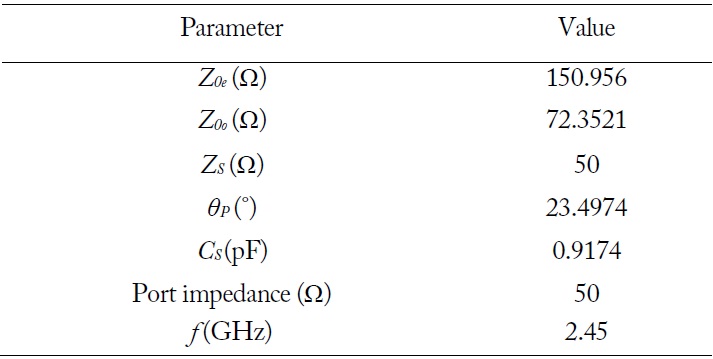
[Table 1.] Arbitrary parameter values for comparison of the parallel coupled line with an open stub (PCL-OS) design equations

Arbitrary parameter values for comparison of the parallel coupled line with an open stub (PCL-OS) design equations

[Fig. 5.] Impedance parameter comparison for ADS, proposed (4a)？(4b), and equations in [2] and [5]. (a) Z11, (b) Z21.

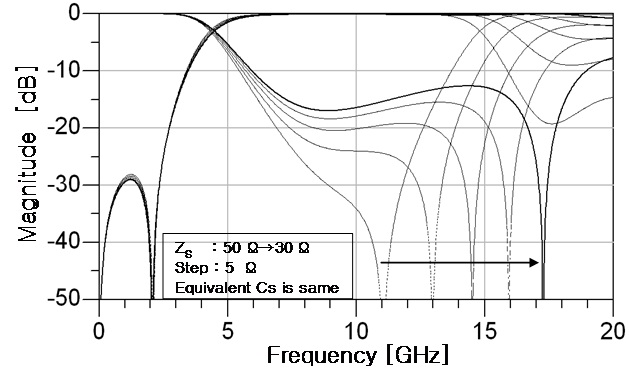
The transmission zero frequency of notch frequency f_n of the LUC is located at the frequency of |S₂₁| = 0.

From the relation [8] between the impedance and scattering matrices, S₂₁ can be obtained as (10)

Then, the notch frequency f_n can be decided by (Z₂₁ = 0) or (Z₂₁≠∞ and Z₁₁ = ∞).

The notch frequency f_n is independently controlled without changing the low pass filter parameters defined above. The open stub has two parameters, Z_S and θ_S, and, hence C_S and f_n can be determined independently. The various f_n examples according to the decreasing Z_S with constant C_S are depicted in Fig. 6.

[Fig. 6.] Notch frequencies according to the decreasing ZS, with constant CS.

III. MICROSTRIP WILKINSON BALUN DESIGN

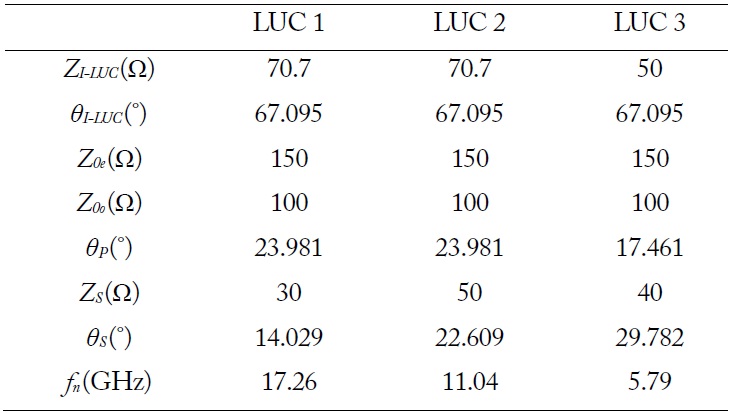
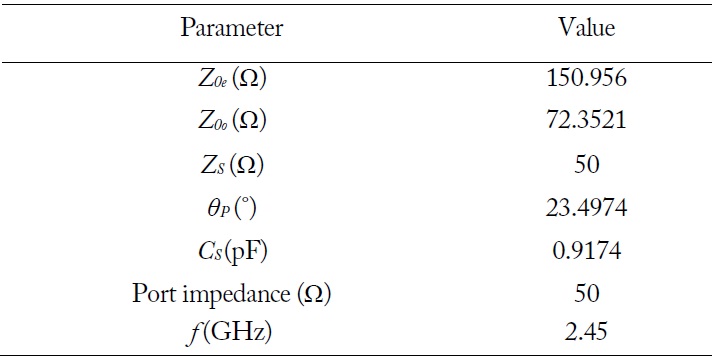
Using the LUC design equations, we designed and fabricated a size and harmonics reduced microstrip Wilkinson balun operating at 2.45 GHz. Fig. 2(b) shows the layout of the proposed Wilkinson balun compared to the CPW-Wilkinson balun [6] of Fig. 2(a). Here, the transmission line sections of the Wilkinson balun are replaced by three LUCs. The LUC 1, 2, and 3 are good for harmonic reduction in S₂₁, S₃₁, and isolation. The LUC’s cutoff frequency f_c must be carefully determined considering the operating frequency band and spurious rejection of the balun. A recommended value is f₀ = f_c +BW/2, where BW is the bandwidth of the balun. For a small pass-band ripple as in Fig. 6, the choice of f₀ = f_c gives also good result.

The LUC is designed using the following procedure:

We designed a T-type Chebyshev low pass filter with a cutoff of 2.45 GHz and a ripple of 0.01 dB. By using the obtained L, and C of the low pass filter, we calculated the LUC parameters shown in Table 2 using the above LUC design procedure for f₀ = 2.45 GHz. For good harmonic suppression, we chose three different f_n values of the LUCs.

[Table 2.] Parameter values of the LUCs for the balun design

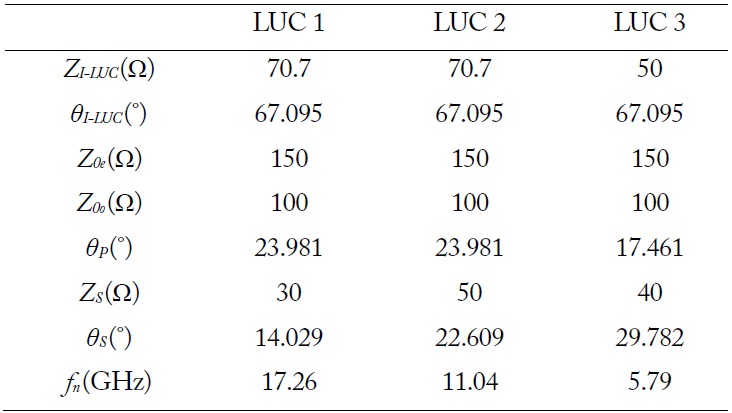
Parameter values of the LUCs for the balun design

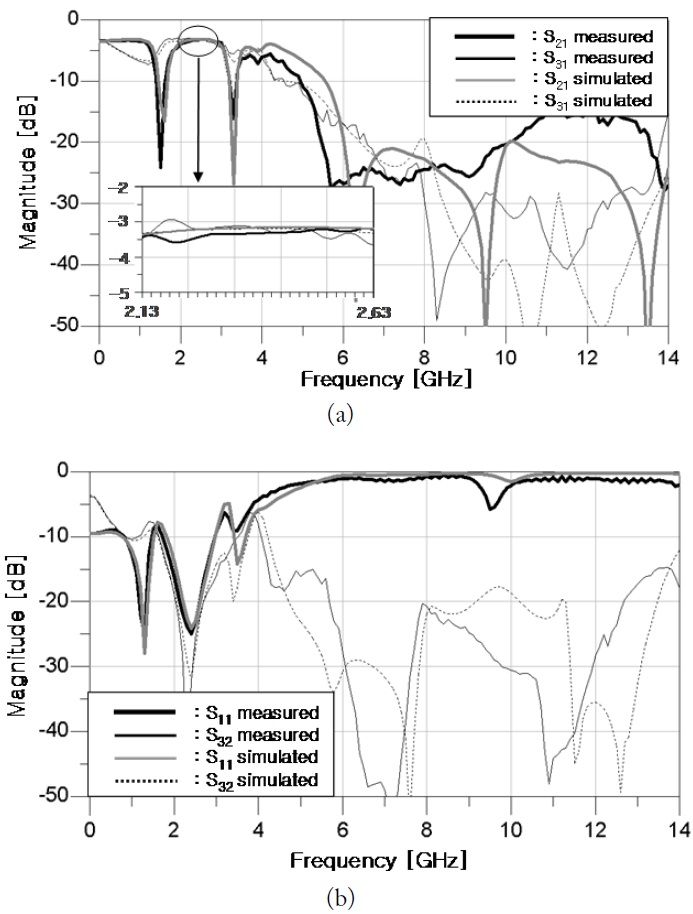
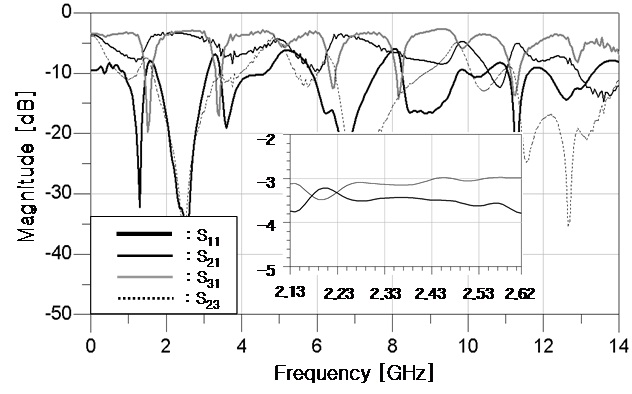
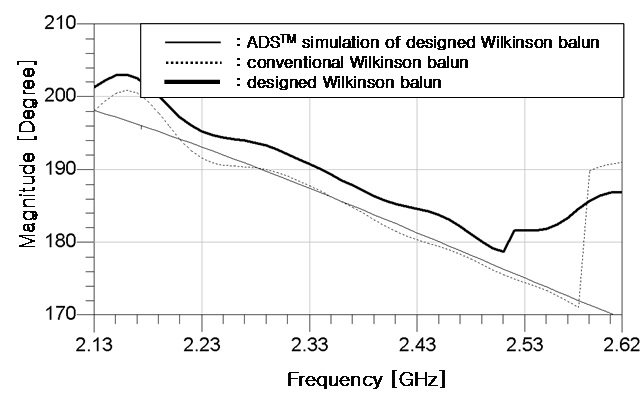
The power division, impedance matching, and isolation properties in a pass-band around 2.45 GHz are as good as a conventional Wilkinson balun. The thickness and relative dielectric constant of the WINUS ISO640-338 substrate used for the simulation and experiment is 0.762 mm and 3.38, respectively. Fig. 7 shows photographs of the proposed and a microstrip version of the conventional CPW-Wilkinson balun [6], which have the center frequency of 2.45 GHz. The area of the proposed microstrip Wilkinson balun is reduced to 48% of the conventional one. The simulated and measured amplitude results are shown in Fig. 8. They agree well with each other on the viewpoints of the power division, the matching, the isolation and the harmonic suppression properties. The measured insertion losses in f₀ (including SMA connectors) are 0.308 dB and 0.307 dB at the two output ports, port 2 and port 3. Furthermore, the harmonics and isolation of the proposed Wilkinson balun are suppressed below -15 dB up to 14 GHz. However, the measured result of the conventional Wilkinson baluns in Fig. 9 shows that the spurious harmonics are repeated in the whole frequency band above the pass-band. Fig. 10 shows the simulated and measured output phase differences of the proposed balun and those of the conventional one. They agreed well with each other.

[Fig. 7.] The comparison of the proposed Wilkinson balun and the conventional Wilkinson balun.

[Fig. 8.] Measured and simulated frequency responses: (a) S21 and S31, (b) S11 and S32.

[Fig. 9.] Measurement results of the conventional Wilkinson balun.

[Fig. 10.] Comparisons of the output phase differences.

IV. CONCLUSIONS

The exact analysis of the PCL-OS and an application of the Wilkinson balun are presented. The designed microstrip Wilkinson balun shows a significantly reduced size and a harmonicsuppressed property simultaneously, without degradation of the pass-band performances.

The proposed design equations and the LUC design procedure could be helpful in designing various microwave devices needing size reduction and harmonic suppression, simultaneously.

참고문헌

1. Li R., Kim D. I. 2005 "A new compact low-pass filter with broad stopband and sharp skirt characteristics," [in Proceedings of the Asia-Pacific Microwave Conference (APMC-2005)] P.1450-1452
2. Li R., Kim D. I., Choi C. M. 2006 "Compact structure with three attenuation poles for improving stopband characteristics," [IEEE Microwave and Wireless Components Letters] Vol.16 P.663-665
3. Hsieh M. Y., Wang S. M. 2005 "Compact and wideband microstrip bandstop filter," [IEEE Microwave and Wireless Components Letters] Vol.15 P.472-474
4. Lee H. S., Choi K., Hwang H. Y. 2007 "A harmonic and size reduced ring hybrid using coupled line," [IEEE Microwave and Wireless Components Letters] Vol.17 P.259-261
5. Zhang J., Li L., Gu J., Sun X. 2007 "Compact and harmonic suppression Wilkinson power divider with short circuit anti-coupled line," [IEEE Microwave and Wireless Components Letters] Vol.17 P.661-663
6. Lim J. S., Yang H. S., Lee Y. T., Kim S., Seo K. S., Nam S. 2004 "E-band Wilkinson balun using CPW MMIC technology," [Electronics Letters] Vol.40 P.879-881
7. Lim J. S., Kim D. J., Jeong Y. C., Ahn D. 2005 "A sizereduced CPW balun using a “X”-crossing structure," [in Proceedings of the 2005 European Microwave Conference] P.521-524
8. Bemani M., Nikmehr S., Takfallah H. 2014 "Dual-band microstrip-to-coplanar stripline Wilkinson balun using composite right- and left-handed transmission lines and its application in feeding dual-band bow-tie antenna," [IET Microwaves, Antennas & Propagation] Vol.8 P.532-540
9. Matthaei G. L., Young L., Jones E. M. T. 1980 Microwave Filter, Impedance Matching Networks, and Coupling Structures.

이미지 / 테이블

[ Fig. 1. ] (a) The structure of the parallel coupled line with an open stub (PCL-OS). (b) The equivalent T-network and (c) equivalent low pass filter unit cell (LUC) block.
[ Fig. 2. ] (a) The microstrip version of [6, 7] and (b) the proposed microstrip Wilkinson balun.
[ Fig. 3. ] (a) Parallel coupled line. (b) Equivalent circuit for Fig. 1(a).
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 4. ] A transmission line and its T-type equivalent circuit.
[ ]
[ ]
[ Table 1. ] Arbitrary parameter values for comparison of the parallel coupled line with an open stub (PCL-OS) design equations
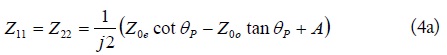
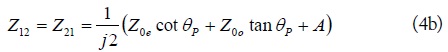
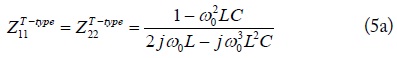
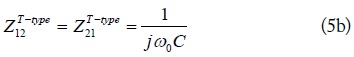
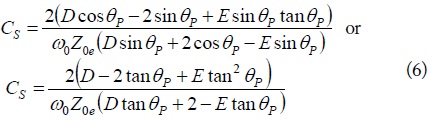
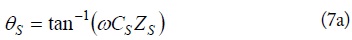
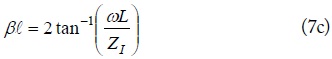
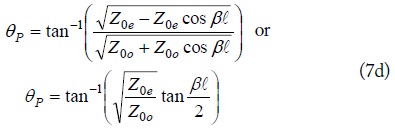
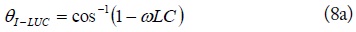
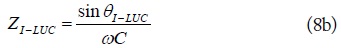
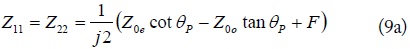
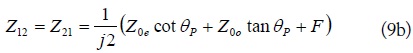
[ Fig. 5. ] Impedance parameter comparison for ADS, proposed (4a)？(4b), and equations in [2] and [5]. (a) Z11, (b) Z21.
[ ]
[ Fig. 6. ] Notch frequencies according to the decreasing ZS, with constant CS.
[ Table 2. ] Parameter values of the LUCs for the balun design
[ Fig. 7. ] The comparison of the proposed Wilkinson balun and the conventional Wilkinson balun.
[ Fig. 8. ] Measured and simulated frequency responses: (a) S21 and S31, (b) S11 and S32.
[ Fig. 9. ] Measurement results of the conventional Wilkinson balun.
[ Fig. 10. ] Comparisons of the output phase differences.