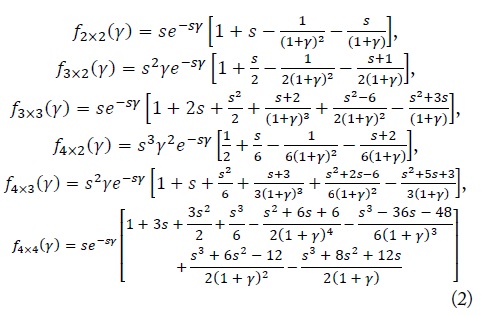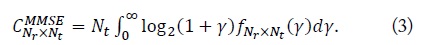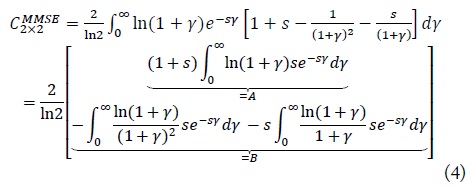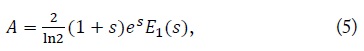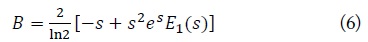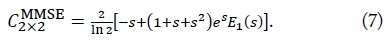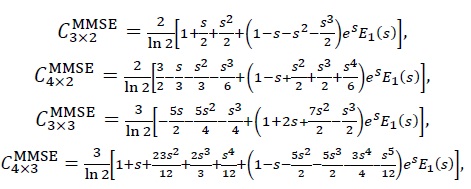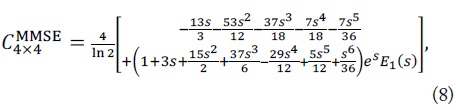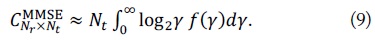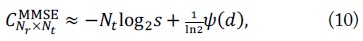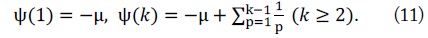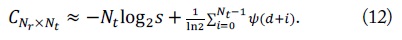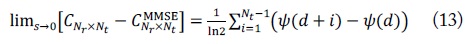The use of multiple antennas at the transmitter and receiver provides a higher capacity than that of a single antenna system [1]. Multiple-input multiple-output (MIMO) communications have been intensively studied over the last few years and are widely considered as suitable for improving performance of modern wireless communications [2].

Maximum-likelihood (ML) detection gives the maximum receive diversity and has high computational complexity. We can apply linear zero-forcing or minimum mean square error (MMSE) detectors to reduce computational complexity. Unfortunately, linear receivers have a smaller diversity order than that of the ML detector.

In [3], the authors derived the achievable instantaneous capacity of a MMSE detector for a given channel matrix H. However, we have introduced the achievable ergodic capacity for an uncorrelated channel matrix H. In this paper, we investigate the analytical measurement associated with MMSE detection. We use the probability density function (PDF) of signal-tointerference plus noise ratio (SINR) [4] to obtain a precise value for the achievable capacity of the MMSE detector. We also derive the achievable ergodic capacity of the MMSE detector at high SNR. Finally, we confirm for a small number of antennas that the difference between the channel capacity and the achievable capacity of the MMSE detector converges to some constant that depends on the number of transmit and receive antennas.

We consider single-user communications and investigate a point-to-point link, where the transmitter is equipped with N_t antennas and the receiver employs N_r(≥N_t) antennas. Suppose that no inter-symbol interference (ISI) exists. Let h_ij be the complex-valued channel coefficient from transmit antenna j to receive antenna i. If the complex modulated signals are transmitted via the N_t antennas, then the received signal at antenna i can be represented as ,where n_i represents additive white Gaussian noise. This relation is easily written in a matrix form as

where denotes the received complex vector, is the transmitted vector with the power is an independent and identically distributed (i.i.d) complex Gaussian fading channel matrix with unit variance, and is an additive white Gaussian noise with zero mean and variance N₀.

Suppose that the transmitter does not know the channel realization. Minimizing the mean squared error (MSE) between the actually transmitted symbol x_i and the output of a linear MMSE detector leads to the filter vector where and h_i is the ith column of H. Applying this filter vector into Eq. (1) yields where and the interference-plus-noise term w is defined as The variance of w is computed as The SINR of a linear MMSE detector on the ith spatial stream can be computed as For the uncorrelated channel, the statistical property of SINR_i is the same for all 1 ≤ i ≤ N_t. Then we omit the subscript i of SINR_i.

We introduce the PDF of SINR at output of linear MMSE detector to calculate the ergodic capacity. We use it for analytical derivation of the ergodic capacity obtained by the MMSE detector. For a high SNR, we will prove that the difference between the channel capacity and the capacity of the MMSE detector converges to the constant that depends only on N_t and d = N_r – N_t + 1.

For small N_r and N_t , we summarize the PDF of SINR [4] as following:

For the uncorrelated MIMO channel, the ergodic capacity achievable by the MMSE detector can be defined as [3]

For example, in N_r 2 and N_t = 2 , we compute the integral directly, as follows:

We can easily check the first term in Eq. (4) by [5, 4.337]:

where and E₁(s) = –Ei(–s) [5]. The second term in Eq. (4) is calculated by integration by parts and [5, 3.352] and then the third one in Eq. (4) is eliminated:

We can obtain the exact ergodic capacity as

In a similar way, can be calculated as the following:

where s = N_t/SNR. Note that is a function of SNR.

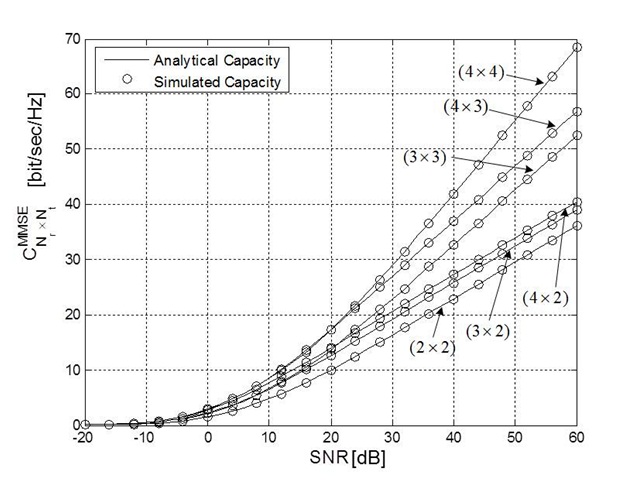
We consider an independent and identically distributed Rayleigh fading channel with N_t. transmit antennas and N_r receive antennas. The simulated capacity performance of the MMSE detector under a typical realization is displayed with respect to SNR. This is validated by the simulation results shown in Fig. 1.

At a high SNR regime, the capacity of the MMSE detector for a MIMO system can be approximated as

Up to N_r = 4 and N_t = 4, by integrating Eq. (9), the approximated ergodic capacities of MMSE detector can be computed easily as

where d = N_r – N_t + 1 and ψ(k) is expressed as [6]

Note that μ is Euler’s constant. In [6], the authors found the approximation for ergodic channel capacity at high SNR as

The difference between the MIMO channel capacity and the capacity of the MMSE detector converges to some constant as

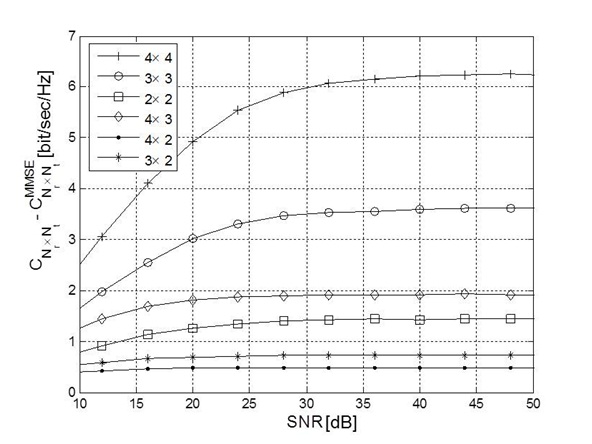
The Eq. (13) shows that the achievable capacity of the MMSE detector has constant capacity degradation. We will validate the capacity degradation by the simulation results shown in Fig. 2.

In this paper, we have studied the achievable ergodic capacity of a MIMO system with a MMSE detector for a small number of antennas. We have also shown that the difference between the channel capacity and achievable capacity of the MMSE detector converges to some constant at high SNR.