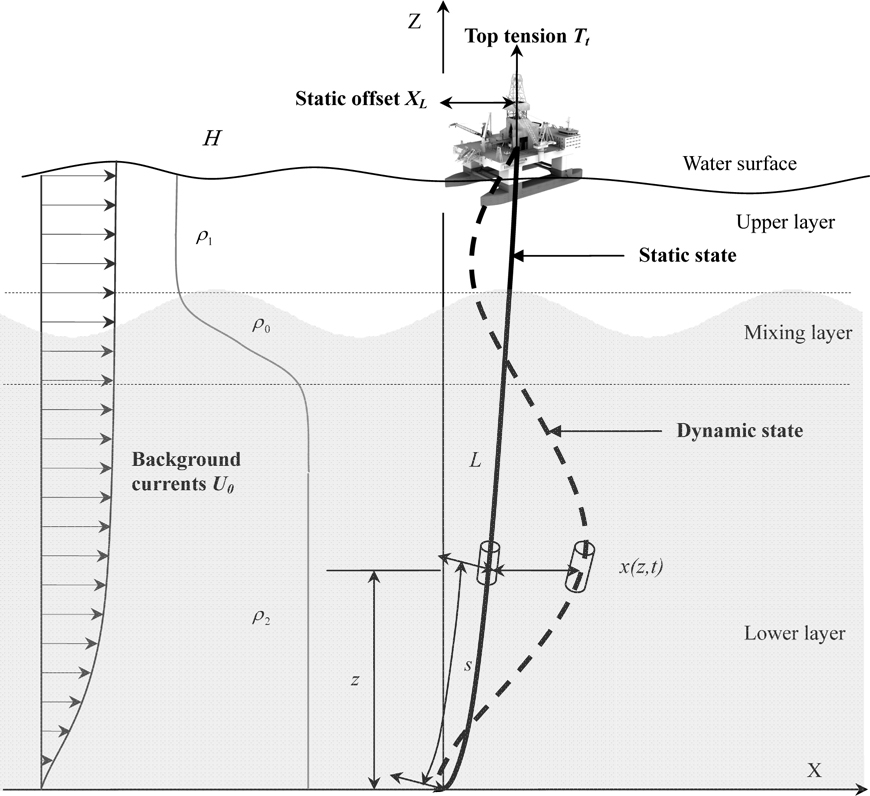
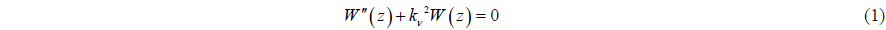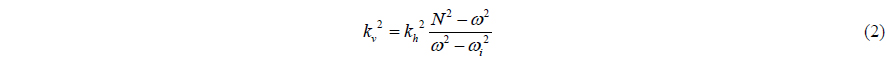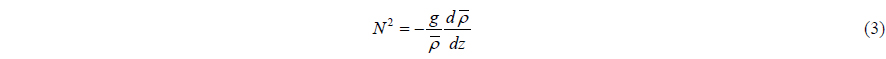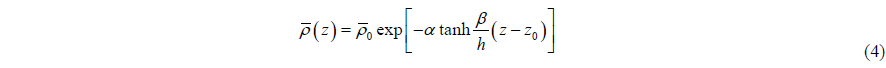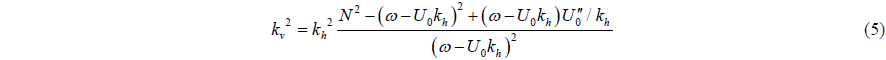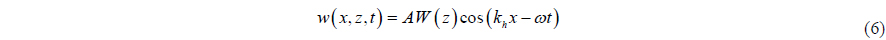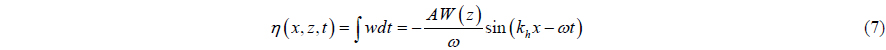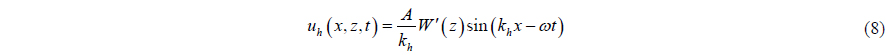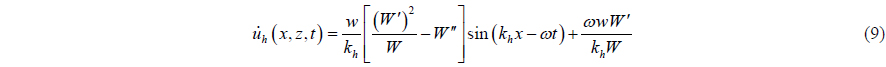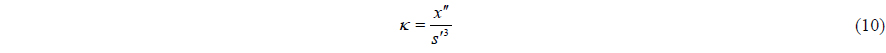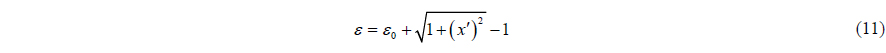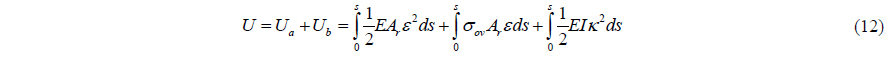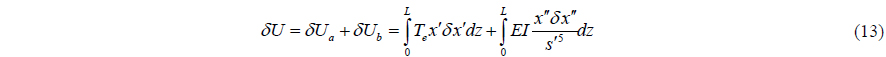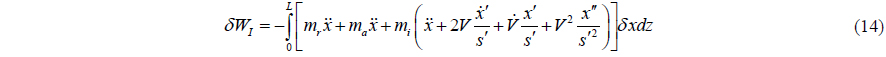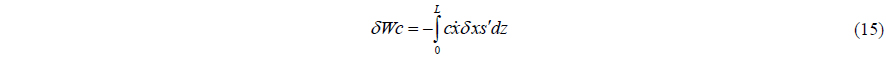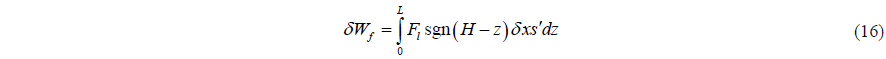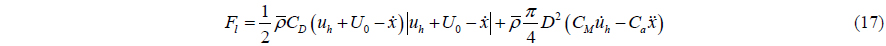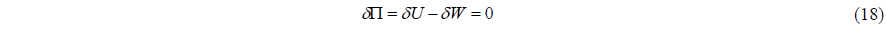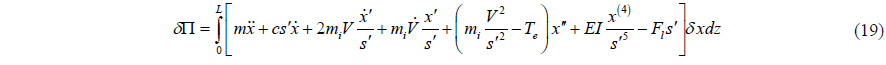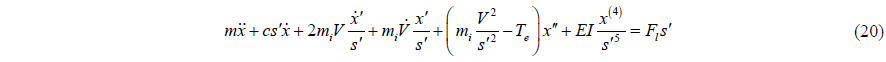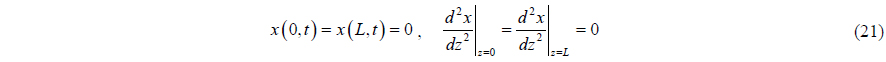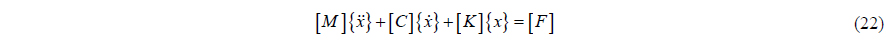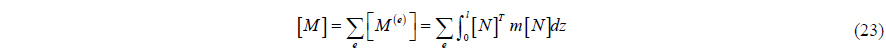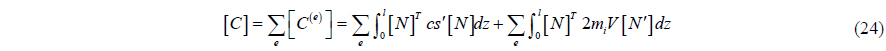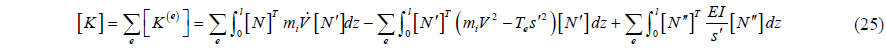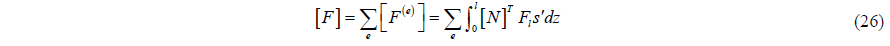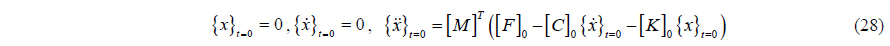Marine risers are important equipment for the exploration of oil/gas in deep water, which usually serve as the bridge between an offshore platform and the well head on the seabed (Kaewunruen et al., 2005; Ju et al., 2012). As exploration activities move into deepwater, the long slender risers tend to undergo large-amplitude motions (Xu et al., 2013). Internal waves are believed to be responsible for a great deal of damage. This is because they can create enormous local loads and bending moments on offshore structures. The internal waves have been reported to induce an additional displacement of 200
The internal waves occur frequently in South China Sea where water is deep (Du et al., 2001). At the current stage, most investigations focus on the generation, propagation, transformation and other properties of internal waves, few studies are related to their effects on offshore structures. Cai et al. (2003; 2008) firstly introduced Morison empirical formula and modal separation method to estimate the forces and torques exerted by internal solitons on cylindrical piles. They found that the background currents will modify the properties of internal waves and enlarge both force and torque (Cai et al., 2006; 2008). Ye and Shen (2005) calculated and analyzed the force of internal waves on small-scale cylinder in different frequencies and then compared with that of surface waves and currents. Du et al. (2007) found that the maximum total force caused by a soliton of a current with speed of 2.1
In this study, the finite element method is applied to calculate the dynamic response of a marine riser conveying fluid subjected to internal waves and background currents. The basic equations of internal waves should be modified if background currents are considered. Thus, it is instructive to demonstrate the effect of background currents on the dynamic response exerted by internal waves on a supposed riser for comparison with no current case. The schematic diagram for a marine riser conveying fluid in internal waves and background currents is shown in Fig. 1. In sections 2 and 3, the governing equation of internal waves, the differential motion equation of a marine riser and the solution methods are presented. The computational results of different cases are discussed in section 4 and the conclusion is given in section 5.
>
Governing differential equation of internal waves
With the Boussinesq and linear approximation, the second-order differential equations govern the vertical structure function
where
In the case of internal waves without background currents, the vertical wave number
where
Consider the dimensional density , which is assumed as Holmboe model, given by (Ye and Shen, 2004):
where is the density of sea water in
However, if the background currents exist, the modified Taylor-Goldstein equation for linear internal waves must be used. Fang et al. (2000) generalize to allow for a background current
where
Eqs. (2) and (4) together with Eq. (1) are introduced to calculate the wave function for the case with or without background currents, respectively. Nevertheless, since it is difficult to express
>
The relative velocity of internal waves
In the two-dimensional Cartesian x, z coordinate system, the water pulsation can be assumed as wave solution and displayed in the form (Ye and Shen, 2005):
where
According to the relation between the vertical displacement of water particles
Note that
Based on the continuity equation for incompressible flow, the horizontal relative velocity
where the small dot ( ⋅ ) represents the derivative with respect to time
VARIATIONAL MODEL OF RISER AND SOLUTION METHOD
The following assumptions are stipulated in the present mathematical model: the material property of the marine riser is homogeneous and linearly elastic and the cross-section are uniform and remain plane perpendicular to the axis at all state; longitudinal strain is large, but the shear strain, torsional deformation and rotational inertia are neglected; the internal fluid is inviscid, incompressible, irrotational, flowing upward and the density is uniform along the riser.
The nonlinear free vibration is determined through the virtual oscillations along the marine riser. The riser will move nonlinearly from the static equilibrium configuration due to small perturbation, as shown in Fig. 1. In the Cartesian coordinates, the normal displacement
According to mathematical model and strain-displacement relationship, when the effect of shear deformation is considered negligible, the curvature of the riser and the axial strain can be expressed as follows:
where
Total strain energy
The total strain energy of a marine riser, which consists of the strain energy due to axial deformation and bending, is given by (Chucheepsakul et al., 2003):
where
By substituting Eqs. (10) and (11) into Eq. (12), the variational expression of the total strain energy is written as:
where the effective tension
Virtual work done by external forces
Needed for dynamic response analysis, the virtual work done due to external forces included inertial force, structural resistance and the hydrodynamic force are taken into account for accurate reckons, i.e.,
where
The virtual work done by the structural resistance is written as:
here
Following is the virtual work done due to hydrodynamic forces that are decomposed into two directions of the water flow velocities. The horizontal direction is considered only and the forces on risers are calculated by Morison formula. Then the work done by hydrodynamic loading is given by:
where
In Eq. (17),
>
Differential motion equation
Based on the principle of virtual work, the total virtual work of the apparent system is zero:
By substituting Eqs. (13)~(16) into (18) and integrating by part, one obtains the total virtual work energy of the riser system expressed as below:
where
Since
While both ends of the marine riser are assumed to be hinged, the boundary conditions are given by:
Discretize Eq. (21) by Hermite interpolation function, obtaining the general form of the finite element method:
where [
where [
Newmark-
To determine the dynamic responses of the riser, the numerical direct integration method is employed in this study. Newmark integration method is found suitable for this problem. The integration constants used are
The initial conditions for determining the dynamic responses of the marine riser are:
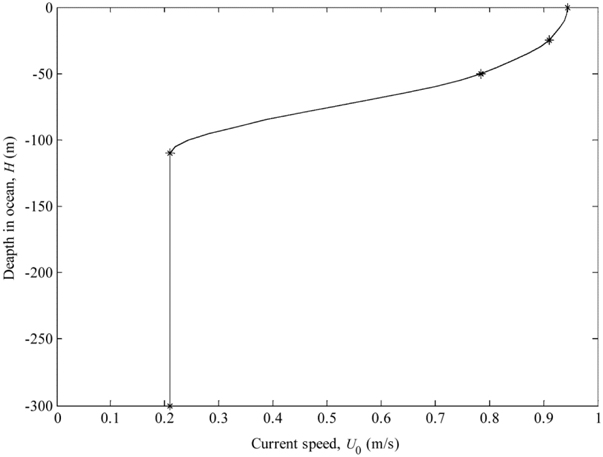
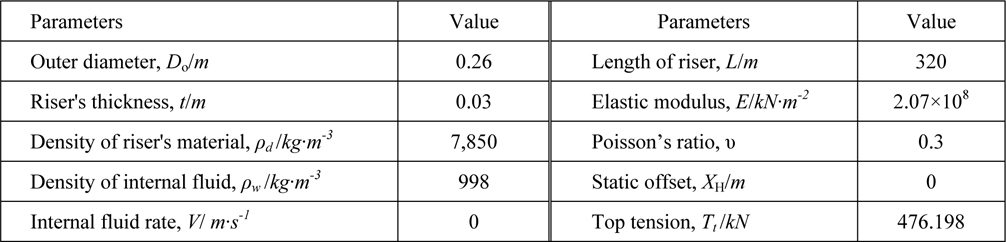
Programs Fre.m and resp.m in MATLAB are developed to solve the natural vibration frequency and the dynamic response of riser in consideration of background currents only. The results of ANSYS analysis which are taking the pipe59 element to simulate and solved by the prestress method are chosen to verify the accuracy of the programs. The parameters of riser and fluid, which are applied in this work, are given in Tables 1 and 2 respectively. The background currents are chosen from the one-year return currents profile in the Liuhua oilfield of South China Sea, as shown in Fig. 2.
[Table 1] Model properties of marine riser.
Model properties of marine riser.
[Table 2] Model properties of seawater.

Model properties of seawater.
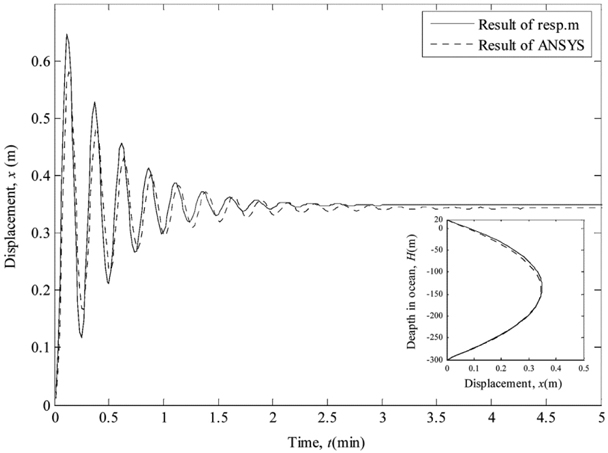
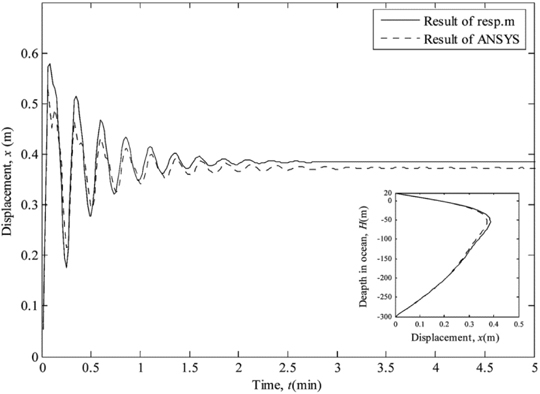
The results in the first six natural frequencies of marine riser are illustrated in Table 3. In addition, the observational background currents and its mean velocity are employed to discuss the effect on the marine riser, as shown in Figs. 3 and 4, respectively. At first, it is found that the riser has a static offset in the uniform background currents. However, the maximum response displacement changes in some vary or degree when the background currents profile are different. The reversal point moves upwards as the background currents concentrate on upper layer, while locates on the center of riser in the mean currents. The Table 3 and Figs. 3 and 4 show a good agreement between the program results and ANSYS software analysis.
[Table 3] Comparison of Riser’s natural vibration frequencies.

Comparison of Riser’s natural vibration frequencies.
>
Dynamic response of riser under internal waves
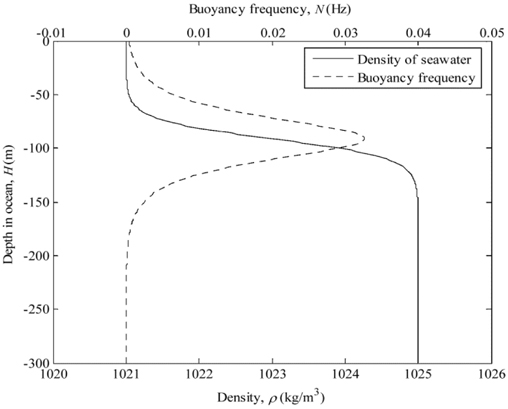
The parameters of Holmboe density distribution in ocean are given in Table 4 (Ye and Shen, 2005). Then, the density distribution profile and the computed buoyancy frequency N are obtained and as shown in Fig. 5. According to vast field observations and investigations of the internal waves in the South China Sea in recent decades (Bole et al., 1994; Qiu et al., 1996; Fang et al., 2000; Li et al., 2003), the internal waves of high frequency (about 3~5
[Table 4] Parameters of Holmboe density distribution.

Parameters of Holmboe density distribution.
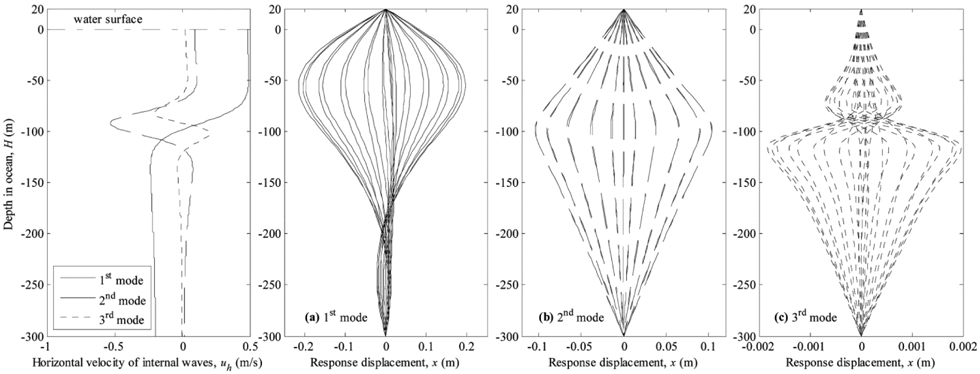
By solving the governing differential equation of internal wave using the Thompson-Haskell method with a vertical resolution of 1
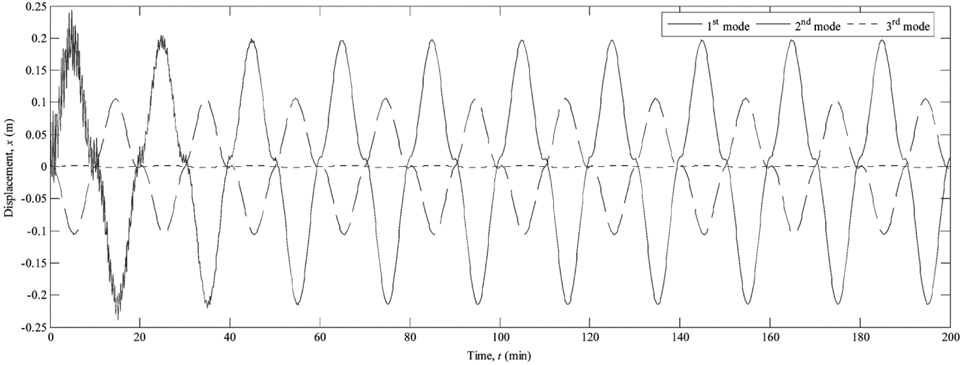
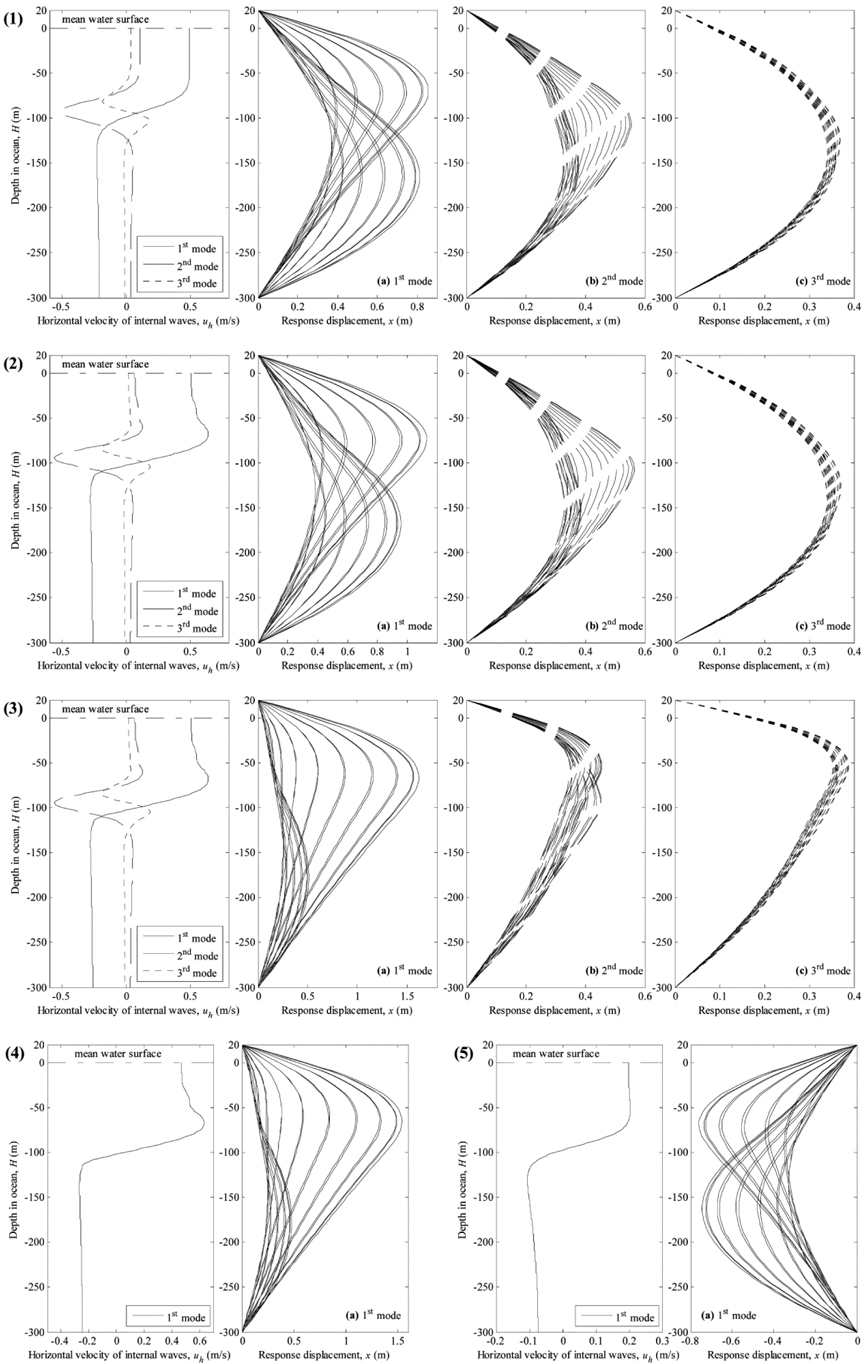
Moreover, Fig. 7 illustrates the time history of response displacement at the reversal point under internal wave alone corresponding to the first three modes. It shows that the oscillating cycles of riser are same as the wave period, and the maximum response displacements are in the same magnitude at the first two modes while rapidly diminish at the third mode. Hence, it suggests that the first two modes of internal waves play dominated role in the dynamic response of marine riser.
>
Dynamic response of a riser under combined excitation of internal waves and background currents
To study the dynamic response of riser under combined excitation of internal waves and background currents, the following five cases are considered as the follows. It should be noted that the main data of internal wave are kept the same as the previous section and the main parameters of uniform currents are taken form Fig. 2
(1) Mean currents, i.e., the velocity
(2) Observational currents, current speed
(3) Observational currents, mean currents speed
(4) Observational currents, i.e., all
(5) Same as case 1 but the currents are in the opposite direction of internal waves.
For all the shear current cases, the local Richardson number
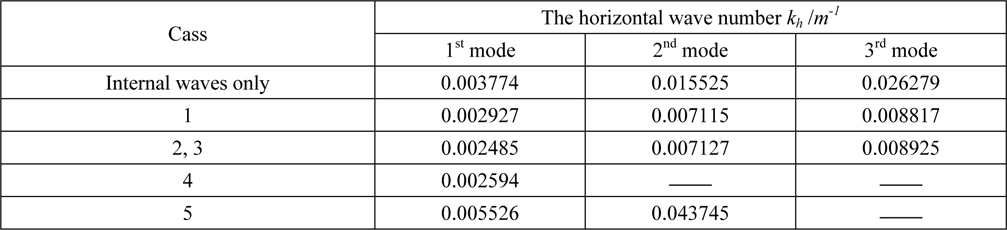
The horizontal wave numbers
[Table 5] The horizontal wave numbers of internal waves in different cases.
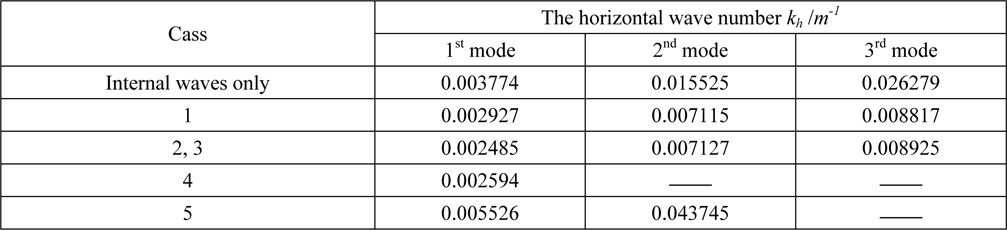
The horizontal wave numbers of internal waves in different cases.
Fig. 8(1) shows the solution in case 1. It is found that the variations in the horizontal relative velocities of internal wave can be ignored. Compared with Figs. 3 and 6, the transfigurations of riser vary greatly. The maximum displacement of riser
When the vertical curvature (
In case 3, mean currents are used to solve the governing equation of internal waves, however, the observational data are served to evaluate hydrodynamic forces on marine riser. As shown in Fig. 8(3), it shows that the maximum displacements
When the observational data is applied to solve the governing equation of internal waves, the eigenfunction (i.e., the vertical wave structure) will break in high mode and only be obtained in the first mode. Fig. 8(4) marks the horizontal relative velocities of internal waves versus depth in the ocean and its effect on the dynamic response of riser. It can be seen that the curve of velocity is rougher than case 2. The maximum displacement reduces by 0.08
Fig. 8(5) displays the horizontal relative velocity profile of the internal waves and the displacements along the riser at different times. In this case, the waves go against the uniform currents. It is found that the relative speeds of internal waves are lower than the other cases. Meanwhile, the maximum response displacement
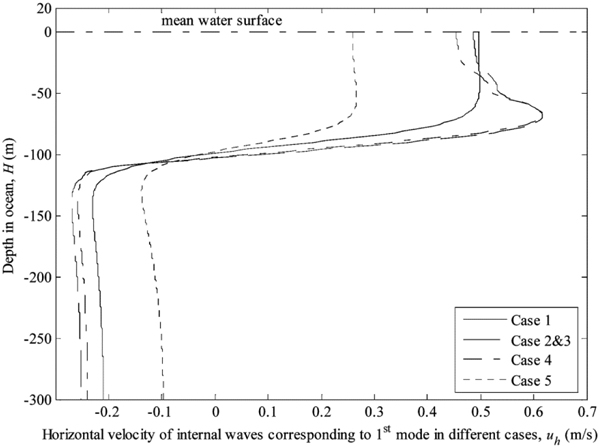
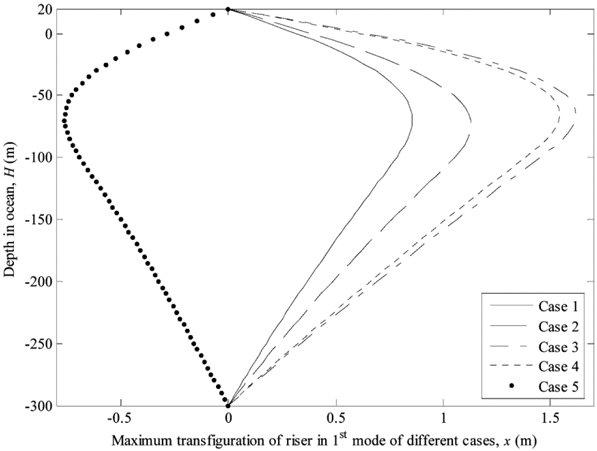
As mentioned above in 5 cases, it is found that the internal waves will exhibit significant effects on riser motions in the 1st mode, when background currents exist. In order to observe and compare the changes in different cases more conveniently, herein, the velocity profile of internal waves and maximum transfigurations of riser corresponding to 1st mode are plotted on a graph, respectively, as shown in Figs. 9 and 10. It can be seen from Fig. 9 that the maximum horizontal relative velocity profile of internal waves have fewer changes on the whole in different cases except the case that internal waves propagate in opposite direction to currents, while the extreme values, which are 0.50
In this paper, the dynamic performance of a marine riser under combined excitation of internal waves and background currents are presented. The dispersion relations and relative velocities of internal waves in horizontal plane are obtained, by solving the geometrically nonlinear equation for riser motion. The numerical solutions about displacement and transfiguration of riser with elapsing time are analyzed. The following conclusions have been drawn:
(1) Without background currents, the internal waves in the first two modes play a dominated role in dynamic response of a marine riser. The displacement of the riser diminishes rapidly in higher modes.
(2) The background currents will make waves that go along them get stretched and waves against them shrunk, which is in agreement with other investigations (Fang et al., 2000). Moreover, the displacements of the riser caused by internal waves in the first mode have an enormous increase when background currents exist. In this case, the distribution of both the currents speed
(3) When background currents exist, the method that the mean value of observational currents speed are used to calculate the internal waves velocity field, while actual value is applied to evaluate the hydrodynamic force is reasonable and applicable in dynamic response analysis of riser, and it is simple and convenient for application in engineering. Meanwhile, the vertical curvature should not be neglect.
(4) The displacements of the riser enlarge greatly, no matter whether the internal waves propagate along or against the direction of background.