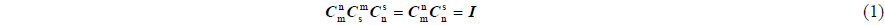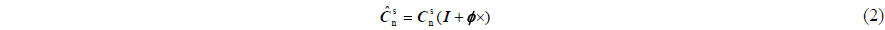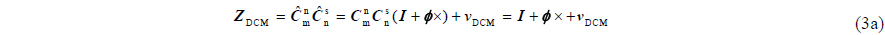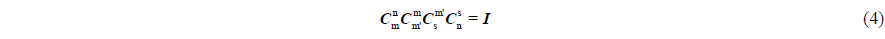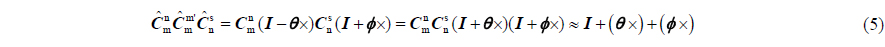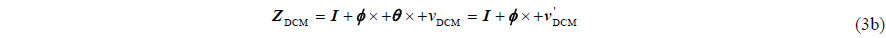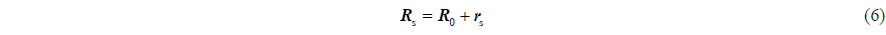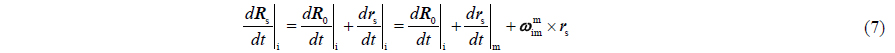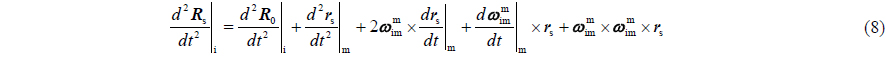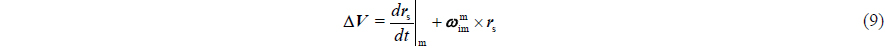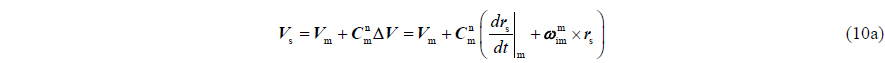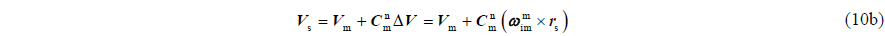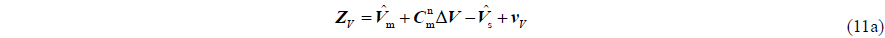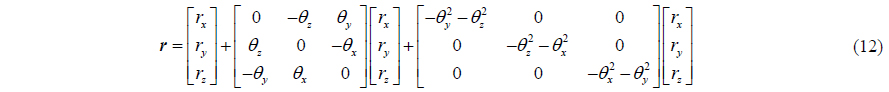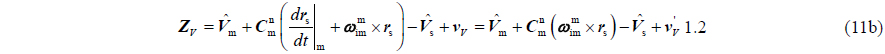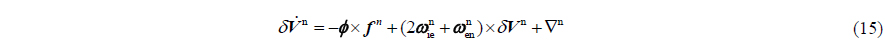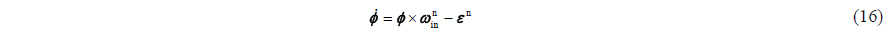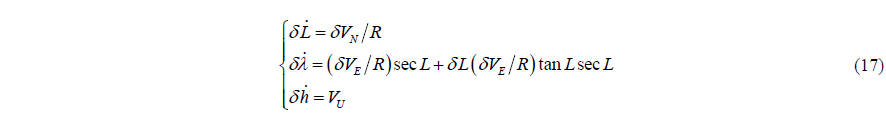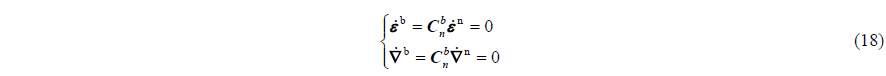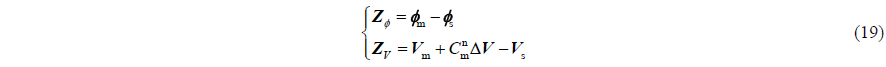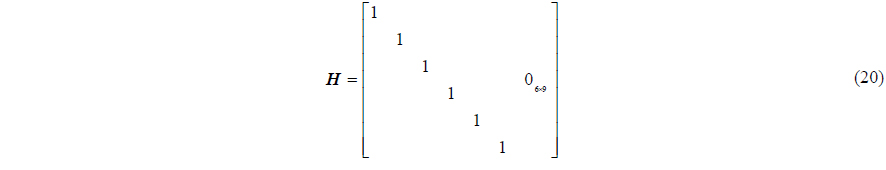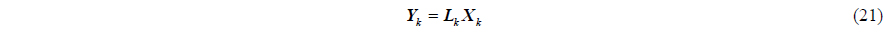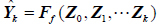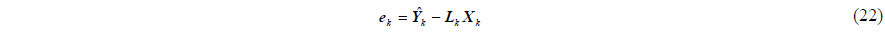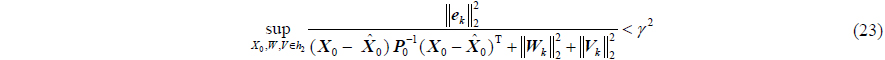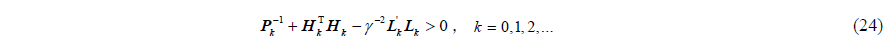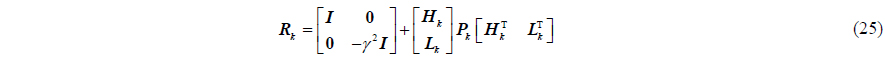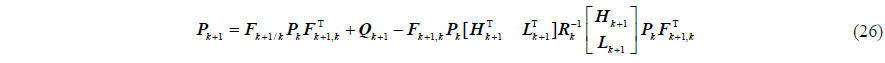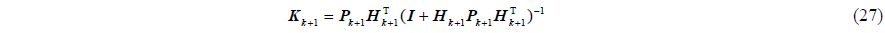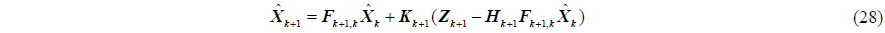On ship, high accurate information from Master Inertial Navigation System (MINS) can be used to fulfill initial alignment for Slave Inertial Navigation System (SINS) composed of low or medium inertial sensors (Titterton and Weston, 2004; Wan and Fang, 1998; Kain and Cloutier, 1989; Shortelle et al., 1998; Grewal et al., 1991). In the integrated system of M/S INS, Kalman filter is often used as an observer, and the differences of velocity, attitude, angular rate and acceleration between MINS and SINS are used as measurement data (Titterton and Weston, 2004; Wan and Fang, 1998).
In the M/S integration, the acceleration or velocity matching method can achieve its alignment goal in horizontal linear accelerated motion, as the angular rate or attitude matching method can do in horizontal angular motion (Lyou and Lim, 2009; Yu, 1988). A transfer alignment system based on combined matching methods can optimize the Kalman filter to outperform all others in arbitrary motions (Lyou and Lim, 2009; Yu, 1988). The best combined matching scheme is known to be the velocity plus attitude, or angular rate plus acceleration (Lyou and Lim, 2009; Yu, 1988; Wan and Liu, 2005; Xiong et al., 2006; GoshenMeskin and Bar-Itazhack, 1992a; 1992b). Flexure deformation, lever-arm velocity and time-delay are known as major error sources for velocity and attitude matching (Lyou and Lim, 2009; Yu, 1988; Wan and Liu, 2005), as instrument error, noise and time-delay are for angular rate plus acceleration (Yu, 1988; Hu et al., 2005; Huang et al., 2005; Lim and Lyou, 2002).
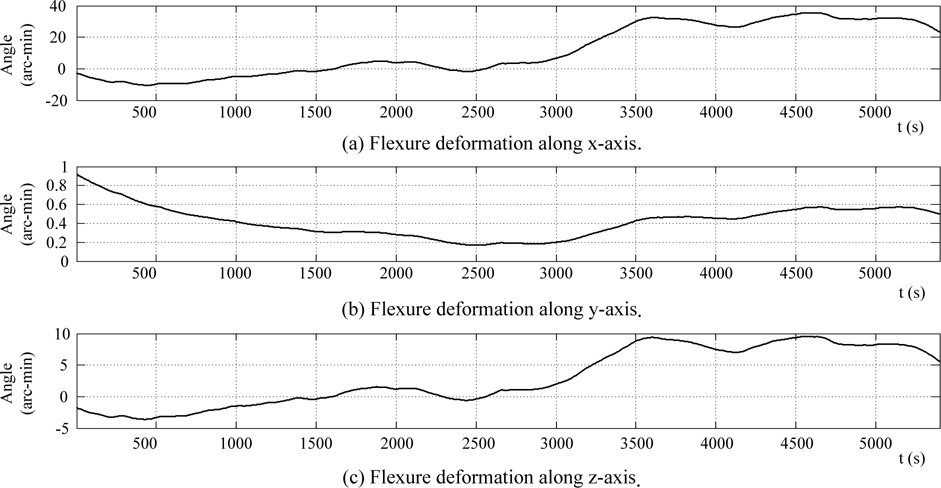
Wan and Liu (2005) gave the measurement data about deck flexure deformation of a medium-sized ship at six sea situation. The deformation around y-axis is 0.05~0.08° when it is about ±1.5
For a given lever-arm length between MINS and SINS, lever-arm effect can be easily constructed and compensated (Wan and Liu, 2005; Hong et al., 2006). Gao et al. (2009) and Liu (2011) pointed out that, when the longer the lever-arm between MINS and SINS and the severer the flexure deformation of ship deck, the more uncertain of lever-arm length will be introduced. So in large ship, if the length of lever-arm is viewed as a fixed value when lever-arm effect is constructed, large measurement error will be introduced and transfer alignment precision will be decreased. Liu (2011) proposed a method to estimate lever-arm length on-line based on acceleration matching. But this method also requires highly precise inertial units, and the accelerometer outputs are easily suffered by noise due to the interference from sway and oscillation (Yu, 1988).
On ship, when communication equipment is fixed in a stable environment, time-delay can be regarded as a constant value, which can be easily compensated. With the above assumption, this paper presents a transfer alignment and fusion algorithm based on “velocity plus attitude” to deal with flexure deformation and lever-arm effect. And SINS is assumed as strapdown INS and MINS is as platform INS.
Lim and Lyou (2002) and Lyou and Lim (2005) introduced
The rest of this paper is organized as follows. In Section 2, attitude matching error caused by flexure deformation is analyzed. In Section 3, the change of lever-arm size change caused by flexure deformation and velocity matching error caused by lever-arm change are studied. In Section 4,
ATTITUDE MATCHING ERROR CAUSED BY FLEXURE DEFORMATION
>
Attitude matching algorithm with no flexure deformation
Ship-based MINS is usually installed at the swing center to measure the overall attitude, velocity and position information, while SINS is usually installed at the head or tail of the ship to measure the attitude and velocity information of the installing position. The schematic diagram of the deck flexure deformation between MINS and SINS is shown in Fig. 1, where m is the MINS body frame, s is the SINS body frame, n is the local horizontal-geographical coordinate frame and navigation frame. In Figs. 1(a) and (b) denote the decks without and with flexure deformation. To a specific ship with limited size, the MINS and SINS have the same navigation frames. is theoretical MINS Direction Cosine Matrix (DCM), and is theoretical SINS DCM. is theoretical DCM between MINS and SINS. When there are no flexure deformation and installing error of SINS, , here “^ ” is a calculated value. In this ideal condition, there exists:
In engineering, the precision of MINS is usually higher than that of SINS by several orders, and then it can be assumed . In SINS, compared with theoretical DCM , there are an initial alignment error, inertial unit concerned error and calculation error in the calculated DCM . Here we assume the installing error is well compensated, can be expressed as follows:
where
In the attitude matching scheme, the measurement information is the difference between MINS and SINS angles, the measurement matrix can be expressed as follows:
where
>
Attitude matching algorithm with flexure deformation
As shown in Fig. 1(b), m' is the flexural body frame and is the flexure deformation matrix between MINS and SINS. is an installing matrix of SINS, and in the case of zero installing error. In the ideal condition, there exists:
If the flexure deformation angle is defined as 𝜽 , there is . In calculation, there exists:
By comparing Eqs. (3) and (5), it can be concluded that, the MINS and SINS angle difference includes the flexure deformation and cannot reflect the change of SINS misalignment angle. In this circumstance, if the DCM of SINS is also driven to be equal to that of MINS, cannot represent the attitude change of SINS installing position, and the navigation function of SINS will not work. When this flexure deformation exists, the real measurement matrix is as follows:
where is the measurement noise matrix. When there is an upper limit of flexure deformation, is color noise with limited energy.
VELOCITY MATCHING ERROR CAUSED BY FLEXURE DEFORMATION
>
Lever-arm velocity calculation between MINS and SINS
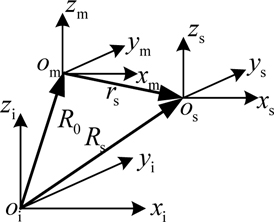
The installation relationship between MINS and SINS is shown in Fig. 2, where i is inertial frame;
In Fig. 2, based on Newtonian mechanics, when the ship rotates relatively to the inertial frames with the angular rate , the relative velocity and acceleration between MINS and SINS can be expressed as follows:
In Eq. (8), the last four elements are defined as lever-arm effect, which are caused by the difference of installing position between two measurement units. With Eq. (8), lever-arm effect can be constructed by and
Traditionally, lever-arm effect is a harmful element, and must be eliminated from acceleration (Kain and Cloutier, 1989; Shortelle et al., 1998; Grewal et al., 1991; Lyou and Lim, 2009; Yu, 1988). However, on large ship, long lever-arm and ship swing would generate a non-ignorable lever-arm velocity at the installing position of SINS. In this case, lever-arm effect in Eq. (8) cannot be eliminated and must be solved as valid measurement information. In order to improve the solving accuracy of pitch and roll and velocity of SINS, especially to restrain the upward velocity divergence, velocity matching is introduced. Pseudo-velocity of MINS in the installing position of SINS can be built by the velocity of MINS and lever-arm velocity.
From Eq. (7), the velocity difference between MINS and SINS can be expressed as follows:
where Δ
where
With no changing in lever-arm size, Eq. (10a) can be rewritten as follows:
In the velocity matching method, the velocity measurement information is as follows:
where
>
Lever-arm velocity error caused by flexure deformation
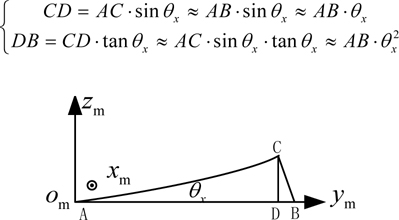
Taking the flexure deformation around x-axis as an example, the lever-arm change caused by flexure deformation is shown in Fig. 3. In this figure,
Similarly, the lever-arm projections in other axes and the lever-arm changes caused by deformation around other axes can be analyzed. If
Eq. (12) indicates that lever-arm size is the function of flexure deformation angle. When there is flexure deformation, in Eq. (10a) is not equal to zero, and the velocity difference in (11a) includes the velocity changes caused by lever-arm changes. If these changes are ignored, estimated errors in misalignment angle and unit error will be produced. So in engineering, there exists:
where is measurement noise. When there is an upper limit of flexure deformation, is color noise with limited energy.
System’s state equation and measurement equation are as follows:
where
System’s state vector can be described as follows:
where
>
Velocity error equation can be expressed as follows:
where
Misalignment angle error can be calculated as follows:
where are angular velocity of navigation frame relative to inertial frame respectively.
Position error equations are as follows:
where
Gyro drift and accelerometer bias are first-order Markov process and can be expressed as follows:
where is the DCM, and in SINS is .
System’s transfer matrix
The “attitude plus velocity” matching method, i.e. taking the difference value of angle and velocity between and SINS as system’s measurement vector, is adopted in the integrated system. There exists:
System’s measurement matrix is as follows:
If the statistics of
>
H∞ sub-optimal filtering equation
where
Supposing that
where
For Eq. (23), the necessary and sufficient condition for solving the
where
where
Ship swinging and translational motions are produced by motion trace simulator, and these motions are used as angle and velocity output by MINS.
Second-order Markov process is used to produce ship body flexure deformation and the flexure deformation angle added MINS angle are used as ideal angle output of SINS. Named lever-arm and flexure deformation angle are used to produce real lever-arm. Then lever-arm velocity can be calculated by real-lever arm size and angular rate of MINS. Lever-arm velocity added the velocity of MINS is used as ideal velocity output by SINS. The ideal inertial unit output of SINS can be calculated by these ideal outputs of SINS with back-stepping navigation solution, and these ideal inertial unit output added white noise are used as the real inertial unit output. With these inertial outputs, SINS solving can be carried, the accuracy of solution and the following filters can be evaluated by comparing these solving output with the ideal output.
Three simulation schemes are established, which are known flexure deformation and the standard Kalman filter, unknown flexure deformation and standard Kalman filter and unknown flexure deformation and
Detailed simulation and filter schemes are shown in Fig. 4.
In the simulation, the ship is assumed to be sailing 45° north by east at the speed of 5
The named lever-arm sizes between MINS and SINS along x~z axes direction are 10
The simulation lasts 5,400
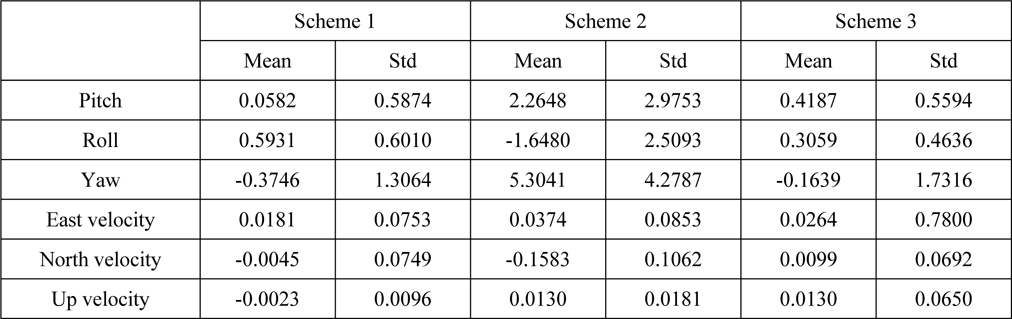
[Table 1] Statistic of error (unit: angle (arc-min) and velocity (m/s)).
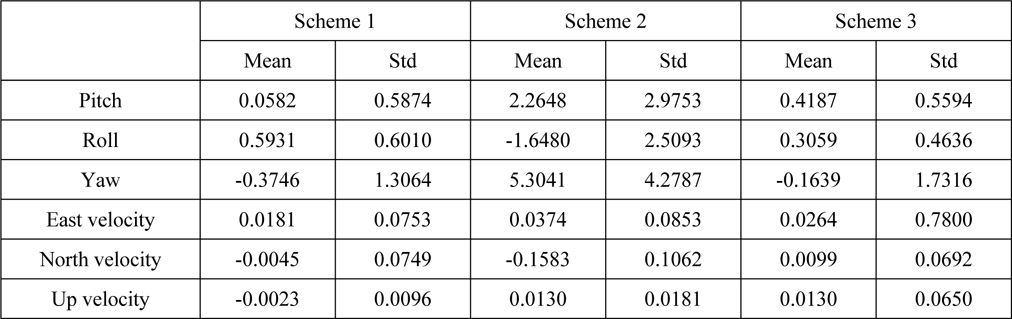
Statistic of error (unit: angle (arc-min) and velocity (m/s)).
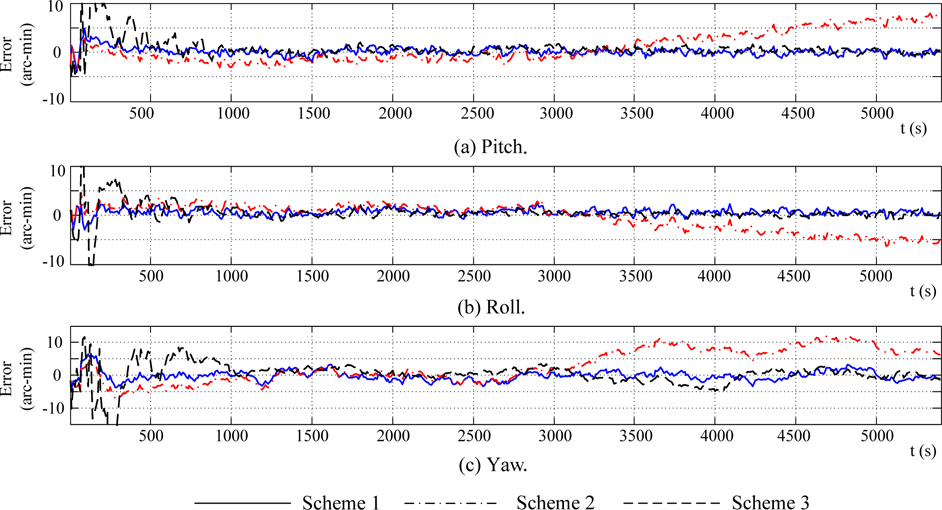
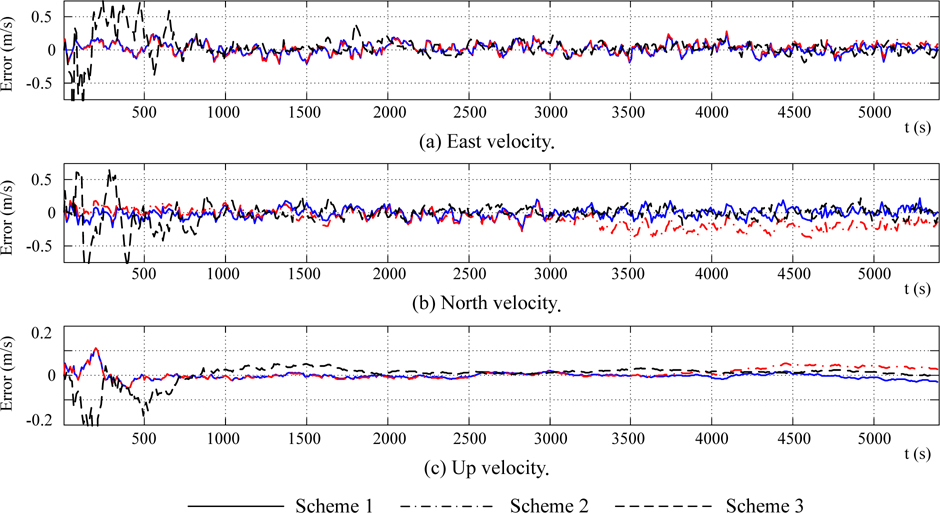
In Figs. 6 and 7, results from solid lines indicate that the effect of standard Kalman filter is excellent when the flexure deformation is well known. In this condition, the impact to angle and velocity matching information caused by flexure deformation can be well compensated.
In Figs. 6 and 7, results from dash lines indicate that when there is non-ignorable flexure deformation, the “attitude plus velocity” with standard Kalman filter cannot estimate the misalignment angle and other error caused by unit error. Generally, if the measured velocity is accurate, velocity matching method can estimate the horizontal misalignment angles. But because of the error in velocity measurement caused by flexure deformation, the curve in Fig. 6(2) with Scheme 2 cannot converge. When ship sailing 45°north by east, flexure deformation around x-axis is projected into east and north, the east and north lever-arm velocity error are brought in, and the horizontal misalignment is caused by the lever-arm velocity errors. So in the east-north-up frame, pitch and roll errors have the same and contrary trend with the flexure deformation around x-axis. When sailing in a constant direction, the yaw error is mainly directed by yaw angle observation. In Fig. 6(3), yaw error curve has the same trend and same magnitude as the flexure deformation with z-axis. Fig. 7 and velocity statistic in Tab.1 show that velocity error all effected by flexure deformation.
In Figs. 6 and 7, result froms dot-and-dash lines show that attitude and velocity error curve slowly converge around zeroes with small oscillation after relatively strong shock at the initial filter period. After about 1000s, the trends of dot-and-dash line coincide with that of solid line, but vibration amplitude is stronger than that of solid line.
The statistics in Table 1 also verifies the above analysis. From the Figs. 6 and 7 and Table 1, it can be concluded that angle and velocity accuracy can be effectively improved by
On ship, especially on large ship, flexure deformation and lever-arm effect are the key factors which decide the actual accuracy of integrated system of M/S INS. Attitude and velocity matching errors caused by deformation is analyzed and simulation results indicate that with “attitude plus velocity”, effective combination of M/S INS cannot be fulfilled. To solve this problem, the