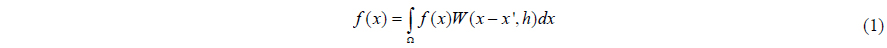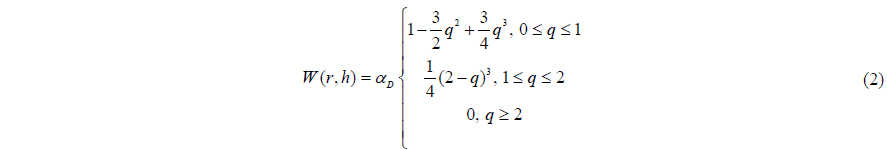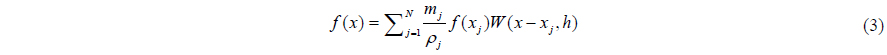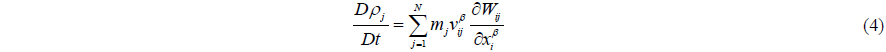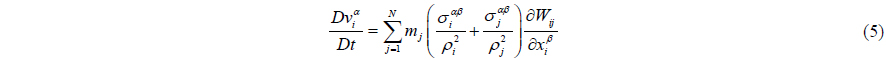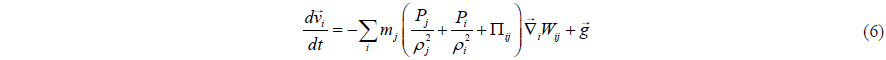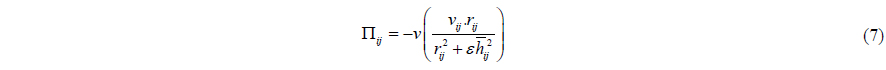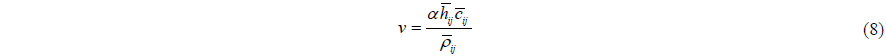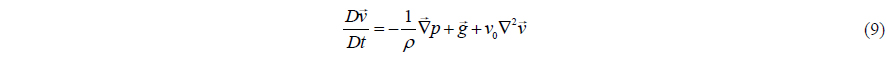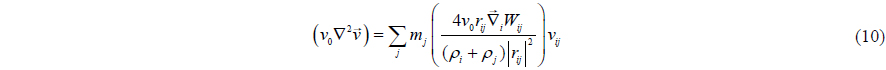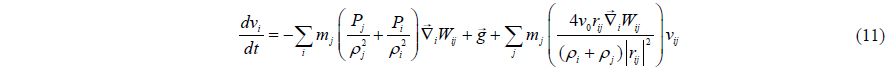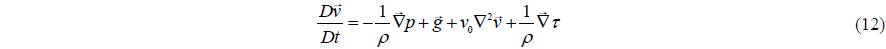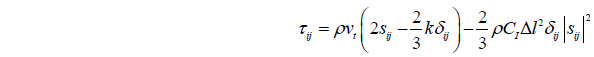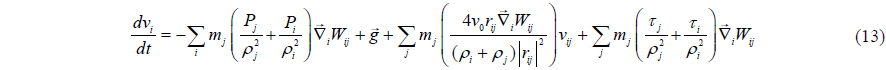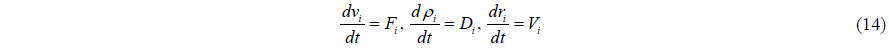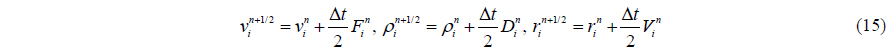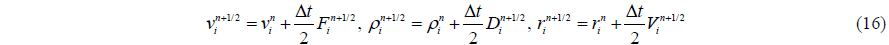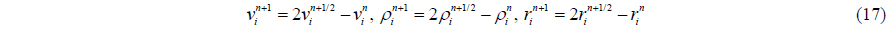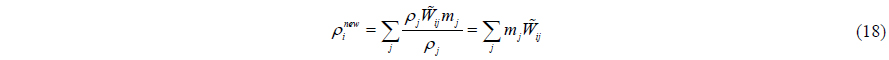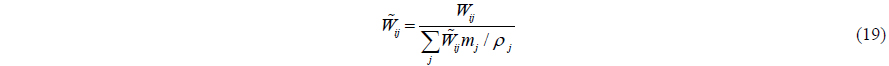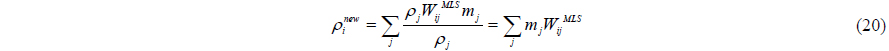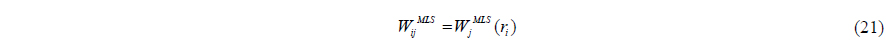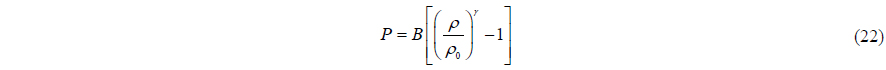Main aim of this paper is to find the best combination of numerical schemes for 2-D SPH simulation of wedge water entry. Diffusion term is considered as laminar, turbulent, and artificial viscosity. Density filter that seriously affects the pressure distribution is investigated by adopting no filter, first order filter, and second order filter. Validation of the results indicates that turbulent model and first order density filter can lead to more reasonable solutions. This simulation was then conducted for wedge water entry with wide range of deadrise angles including 10 degrees, 20 degrees, 30 degrees, 45 degrees, 60 degrees and 81 degrees, with extreme deadrise angles of 10 degrees, 60 degrees and 81 degrees being considered. Comparison of SPH results with BEM solutions has displayed favorable agreement. In two particular cases where experimental data are available, the SPH results are shown to be closer to the experiments than BEM solution. While, accuracy of the obtained results for moderate deadrise angles is desirable, numerical findings for very small or very large deadrise angles are also very reasonable.
Water impact pressure arising during the impact and especially during the initial stages of water entry when the maximum pressure occurs, is extremely important in the design of marine structures. Abrate (2011) has presented an in-depth review of the state of the art on the hull slamming or water entry problem. Based on this article and other recent papers, research conducted in the field of water entry is hereby surveyed.
Initial study of water entry problem for determination of water entry impact forces and pressures was done by Von Karman (1929). He used simple principles such as conservation of momentum and the concept of added mass. Wagner (1932) continued the theoretical solution of water impact problem. He analyzed the vertical water entry of a 2D wedge of small deadrise angle. Sedov (1934), on the other hand, extended Wagner’s work to study the impact of 2D wedge of larger deadrise angle.
In order to simulate the water entry problem, many numerical methods have been implemented by different researchers (Greenhow, 1988; Zhao et al., 1997; Yan and Ma, 2007; Zhang et al., 2010; Ghadimi et al., 2012; Ghadimi et al., 2013). Common methods of simulation have been grid-based. These schemes have encountered some computational difficulties when phenomena such as flow surface piercing, separation and large movement are involved in the modeling. As a result of this, it has become difficult to capture the movement of fluid and free surface flow due to a moving body. To overcome this difficulty, Lagrangian computational method such as Smoothed Particle Hydrodynamics (SPH) was adopted which is a mesh free method. SPH method was first developed for simulation of the particle motion in astrophysics by Gringold and Monaghan (1977) and Lucy (1977). Later, SPH was employed for simulating flow through porous media, large deformation of free surface flows, impact problem, Fluid Structure Interaction (FSI) and water wave generation (Shao, 2010; Dalrymple and Herault, 2009; Ferrari, 2010; Gómez-Gesteira et al., 2005; Gómez-Gesteira and Dalrymple, 2004; Gómez-Gesteira et al., 2010; Monaghan, 1994; Rogers et al., 2008).
Application of the SPH method has also been extended to simulation of water impact problem. Oger et al. (2006) modeled symmetric wedge water impact of 30
SPH method was also previously used by the current authors in order to simulate hydrodynamic phenomena and a particular WCSPH code was developed. This code has been considered and validated in two stages and for different applications: (1) the produced free surface elevation was validated by a dam-break problem (Ghadimi et al., 2012), and (2) the obtained pressure distribution was validated by a planing flat plate problem (Ghadimi et al., 2012). Based on these studies, it is clear that the WCSPH method is quite appropriate for accurately simulating the water entry problem. In the present study, the developed WCSPH code is used in order to investigate wedge water entry at a wide range of deadrise angles ranging from very small to moderate and to very large angles to find the best numerical schemes within SPH formulation. Accordingly, water impact of 2D wedge of 45
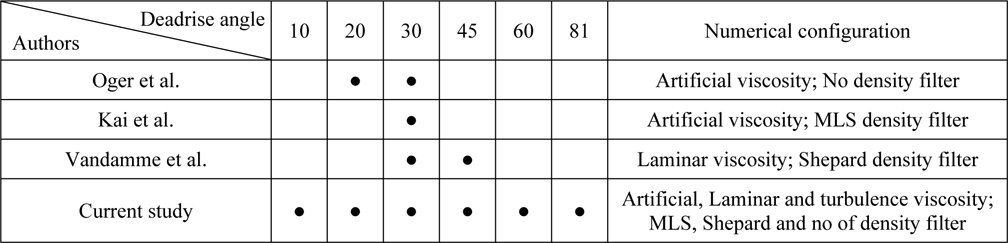
[Table 1] Summary of wedge water entry studies by SPH method.
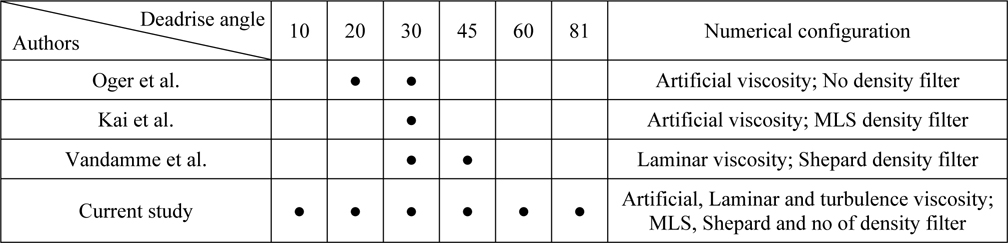
Summary of wedge water entry studies by SPH method.
Based on the comparison presented in Table 1, one can conclude that the current SPH simulations of wedge water entry include a much wider range of deadrise angles (10
>
Integral presentation of a function
SPH interpolation of a quantity
where the function
In this study, cubic spline is used as a kernel function which is given by
where
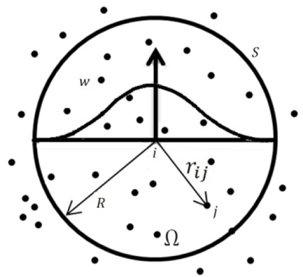
To apply SPH interpolation for a fluid flow, computational domain is divided into a set of particles, as shown in Fig. 1. Every element has a mass
where
Fundamental physical laws of conservation are the basic governing equations of fluid dynamics which are conservation of mass, momentum and energy. For this problem, conservation of mass and momentum should be used.
In the SPH method, derivative of the density for particle
where the sum extends over all neighboring particles and
Also, velocity can be found from the momentum equation (Monaghan, 1994) as in
NUMERICAL FORMULATION OF SPH METHOD
To consider the diffusion term in the momentum equation, three different approaches including (1) artificial viscosity, (2) laminar viscosity and (3) laminar viscosity plus sub-particle scale turbulence, are investigated.
Artificial viscosity
Monaghan (1992) introduced the artificial viscosity. Based on this concept, the momentum conservation equation can be written as
where is the gravitational acceleration.
The viscosity term, Π
where 𝜖 ~ 0.01 is introduced to prevent a singularity when
where and
Laminar viscosity
Momentum equation in the form of laminar viscous stresses is given by
Laminar stress term is simplified by Lo and Shao (2002) to
where
Laminar viscosity and sub-particle scale (SPS) turbulence
Gotoh et al. (2004) introduced Sub-Particle Scale approach for modeling the turbulent effects. Momentum conservation equation can be presented as
where 𝜏 represents the sub-particle scale stress tensor.
The eddy viscosity assumption is used to model the sub-particle scale stress tensor
where
SPH algorithm reduces the original partial differential equations to a set of ordinary differential equations. Then, any time stepping scheme for ordinary differential equations can be used.
In this study, Predictor-Corrector algorithm is used. The momentum, density and position equations can be rewritten in the following form:
where
Based on Eq. (14), Predictor-Corrector scheme predicts the evolution in time, as in
Also can be calculated according equation of state by Gomez-Gesteira et al. (2010). These values are then modified using forces at the half step, as in
At the end of any time step, the values are calculated as in
The pressure is calculated from density using
In the SPH simulation, pressure oscillations may be observed in the obtained results. To overcome this difficulty, Colagrossi and Landrini (2003) applied a filter over the density of the particles and re-assigned a density to each particle. In the current paper, zero order filter and first order filter are considered as compiling options.
The following procedure is known as zero order filter and is applied every 100 time steps:
where the kernel has been corrected using a zeroth-order correction:
Dilts (1999) developed the first order filter (moving least squares filter). This filter was applied successfully by Colagrossi and Landrini (2003) and Panizzo (2004). First order filter is a first order correction. Thus, the linear variation of the density field can be exactly reproduced as
The corrected kernel is also evaluated as follows:
In the studies conducted by Monaghan (1994) and Batchelor (1974), the relationship between pressure and density is assumed to be
which is known as Tait's equation of state. Coefficient
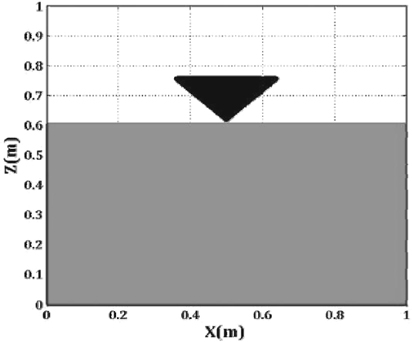
The geometry of the considered problem is illustrated in Fig. 2. Width and height of the domain are equal to 1
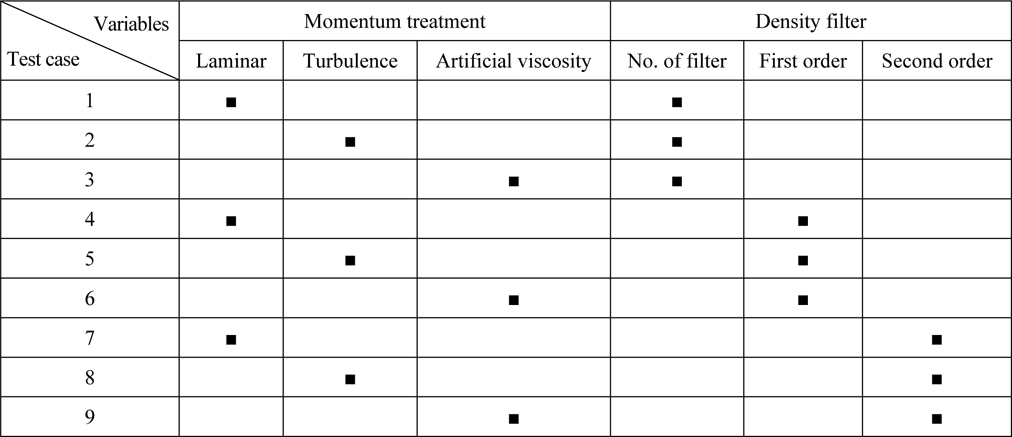
In the current study, the effects of density filter and viscosity treatment have been examined. Combinations of these parameters for each considered case is shown in Table 2. Focus of this study is on the accuracy of pressure distribution. Pressure distribution was also measured and compared with similarity solution of Zhao et al. (1997). Similarity solution is obtained through an analytical process and has been used by many researchers like Dobrovol’skaya (1969) and Zhao et al. (1997) to study water entry problem. Through this method, pressure distribution on the wedge can be calculated.
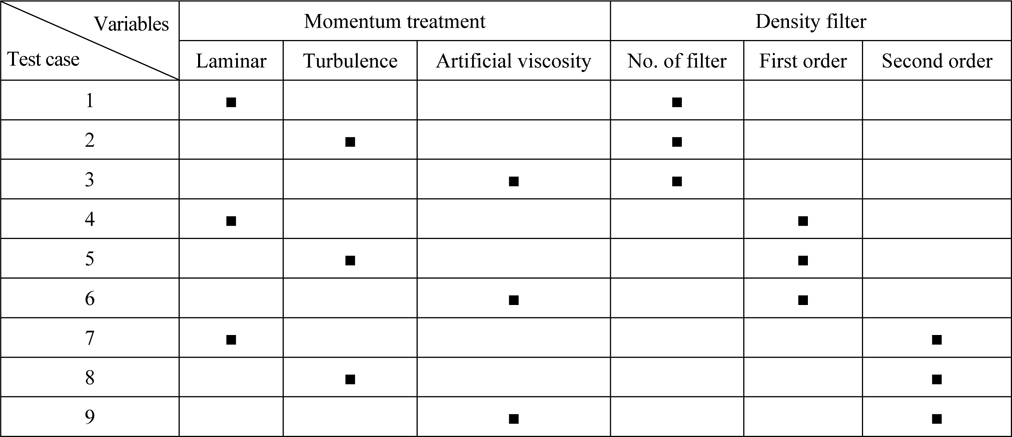
Compiling options.
In the present work, pressure distribution of the wedge water entry is studied. Nine tests including entry of constant velocity of wedge of 45
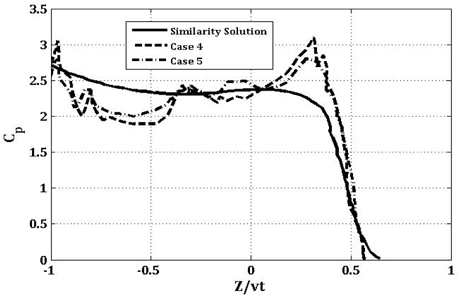
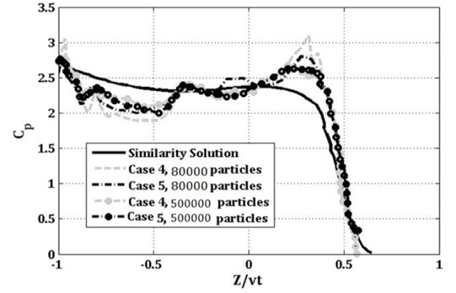
It is quite apparent that the momentum treatment can affect the free surface level. Comparison of the obtained results of free surface against other numerical results (Muzaferija et al., 1999) shows that the obtained free surface level by laminar and turbulent viscosity is better than the artificial viscosity. The results in cases 4 and 5 also have good agreement with other results (Muzaferija et al., 1999). Pressure distribution in cases 4 and 5 are compared with similarity solution (Zhao et al., 1997) in Fig. 4. There is no critical difference between the obtained results of cases 4 and 5. Therefore, it is concluded that both laminar viscosity and turbulent viscosity can be used to simulate the water entry problem, because the duration of this phenomenon is very short.
In order to obtain more accurate pressure distribution, cases 4 and 5 with about 500,000 particles were repeated again. These results are presented in Fig. 4. On the horizontal axis, Z/vt is the non-dimensional length in which v is the entrance velocity of the wedge and t is the time at which the maximum pressure occurs.
There seems to be an improvement in the results. As expected, by increasing the number of particles, the difference between the obtained results of laminar viscosity and turbulent viscosity became even more smaller.
It is also quite apparent that turbulent modeling and using first order density filter lead to best results. Therefore, simulation of water entry of wedges of 10
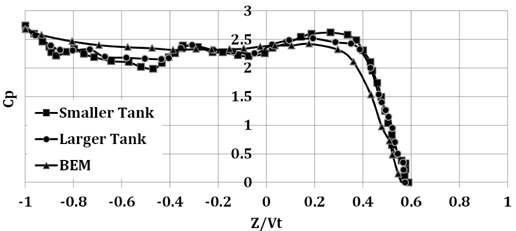
Water impact generates sound wave that reaches numerical domain boundaries. Reflection of this wave from boundaries goes back to the wedge and may affect pressure distribution. Thus, at this stage, tank size increases to 4
Fig. 6 shows the effect of domain size on pressure distribution of the wedge of 45
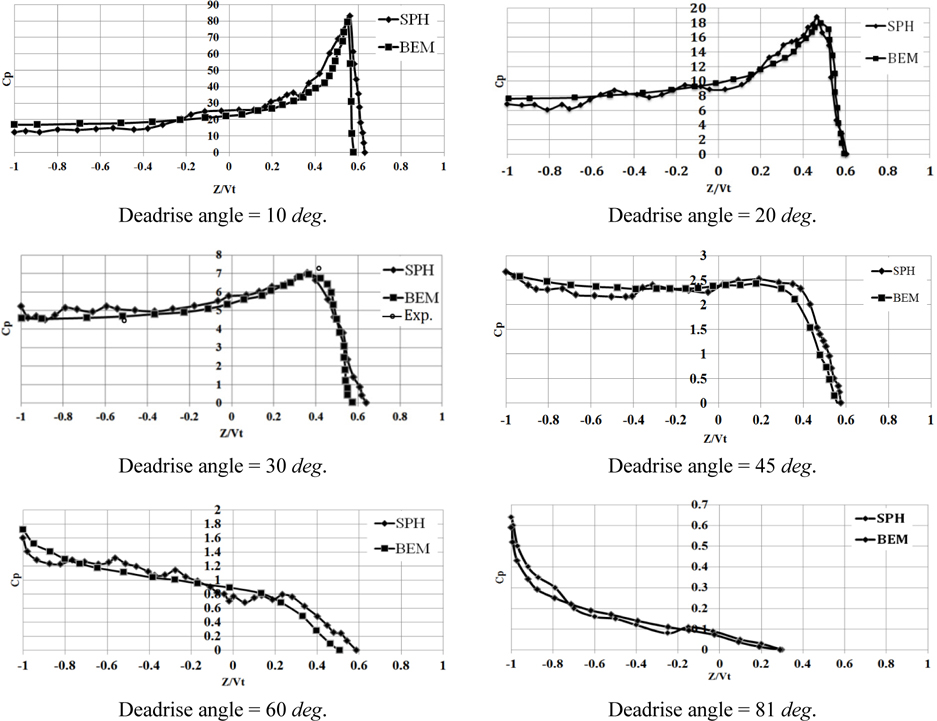
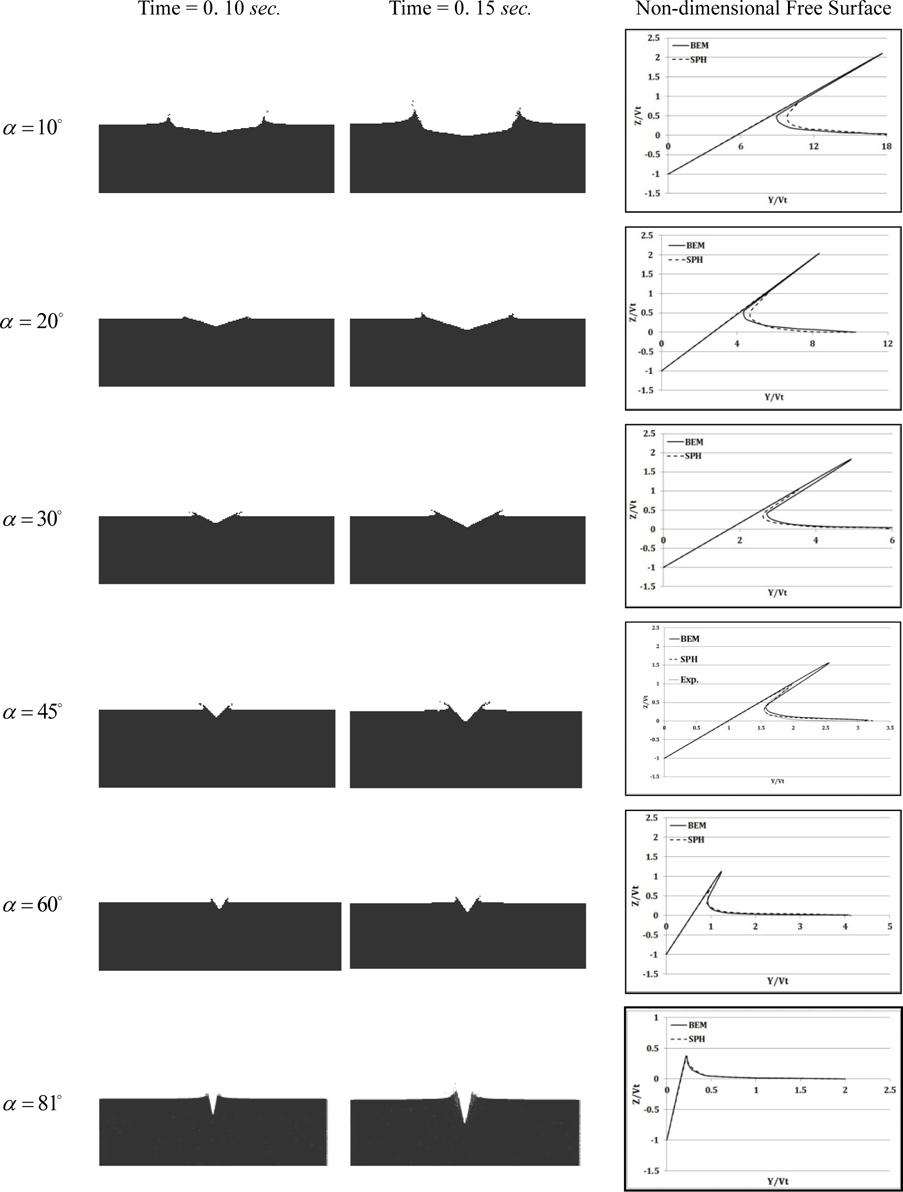
Simulation of wedge water entry of 10, 60 and 81 deadrise angles by SPH method had not previously been reported by other researchers and was conducted in the current study. Pressure distributions of these wedges are presented in Fig. 7. As evidenced in this figure, there is good agreement between the current SPH results and the boundary element solution (Zhao and Faltinsen, 1993). On the other hand, a comparison is presented between the current results and experimental results of Zhao et al. (1997) for the wedge deadrise angle of 30
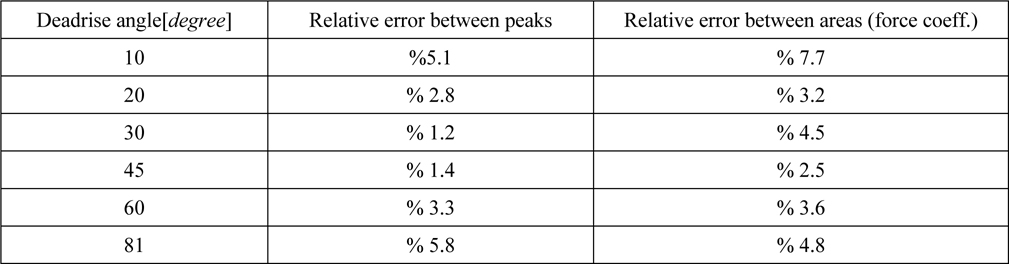
Differences between SPH results and BEM solutions are shown in Table 3. It is observed that at extreme deadrise angles, i.e. 10
[Table 3] Comparison of SPH results and BEM solutions.
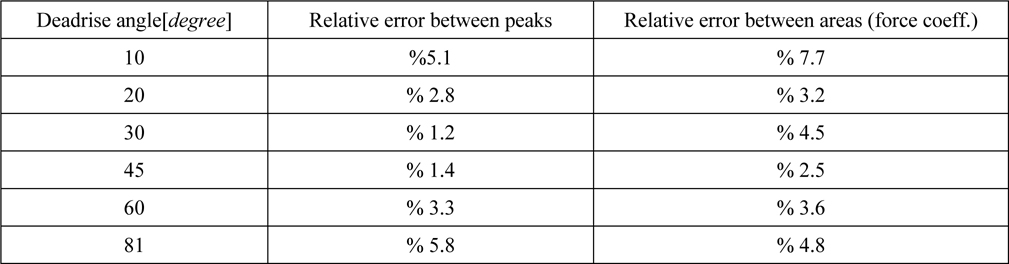
Comparison of SPH results and BEM solutions.
Free surface elevations related to wedges of 10
As evidenced in Fig. 8, favorable agreement is observed between SPH results and BEM solutions. Comparison between the results of the current study against experimental results (Tveitnes et al., 2008) for wedge of 45
In this paper, wedge water entry for a wide range of deadrise angles is simulated by SPH method. In order to find the best numerical configuration, nine different test cases are considered. These cases describe the water entry of wedge of 45
In order to assure that the obtained numerical configuration can also lead to good results for wide range of deadrise angles, wedge water entry of 10
While the achieved numerical configuration within SPH formulation has lead to desirably accurate simulation of wedge water entry for a wide range of moderate deadrise angles, it is also quite apparent that numerical findings for particular cases of relatively small and relatively large deadrise angles are also very reasonable.