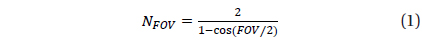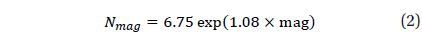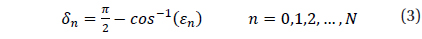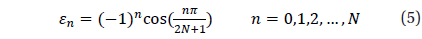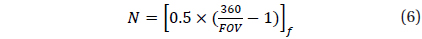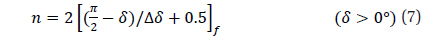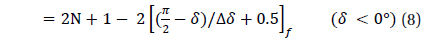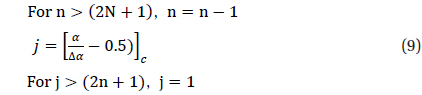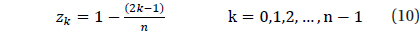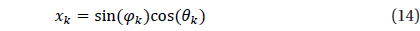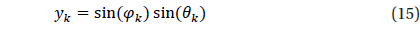The estimation of attitude information is one of the critical issues in the operation of spacecrafts and star sensors. Star sensors obtain the attitude information from the observed stars without priori information to estimate it. The identification of stars in a star sensor is accomplished through a built-in star identification algorithm in the star sensor. In this process, the stars in an observed image and the reference stars catalogued already are compared until those two match each other. There are various star identification algorithms which show differences in the utilized identification information and the pattern of star identification. These algorithms utilize the information of brightness, angular distances between stars, and the angles between star pairs constructed based on a pivot star. Also these algorithms are classified as Triangle, Polygon, and Pivot algorithm according to the combination pattern of recognition information (Groth 1986, Kosick 1991, Liebe 1992, Baldini et al. 1995, Padgett et al. 1997, Liebe 2002).

Match Group Algorithm is a star identification algorithm which has been successfully applied to spacecrafts. It senses the star pivot configuration as a recognition pattern and utilizes the information of the star magnitudes and the angular distances between stars comprising the pattern for the recognition of stars. The usage of pivot pattern in the star identification algorithm was first mentioned as Pole Technique by Kosick (1991) and there was a great improvement through the usage of apparent magnitude as an additional information of identification (Van Bezooijen 1993). The main concept of identification in this algorithm is to identify the pivot star in a pivot configuration and this pivot star is the common star in all the pairs of angular distance. Quite a few stars are required in order to find the pivot star using the angular distance information only which is obtained through pivot configuration. However, when we use the apparent magnitude as in the Match Group Algorithm, the number of stars required for the identification could be reduced to improve reliability and speed of this algorithm. The magnitude of a star is an excellent information of the star and it could improve the performance of a star identification algorithm (Scholl 1995). In order to utilize the apparent magnitude information, the calibration of magnitude is required, which is quite tricky. Also, there still is an uncertainty in the magnitude itself and the sensitivity of sensor degrades as time elapses, the uncertainty in magnitude information could be increased.

In this paper, a study on a star identification algorithm which utilizes pivot configurations instead of apparent magnitude information was performed. In order to identify stars, this new algorithm does not use the apparent magnitude but utilizes the relative brightness and the cell index which is an identification information obtained during the identification processes. This approach improves the reliability and the identification speed.

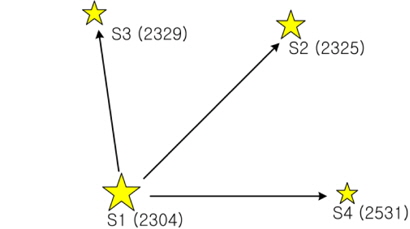
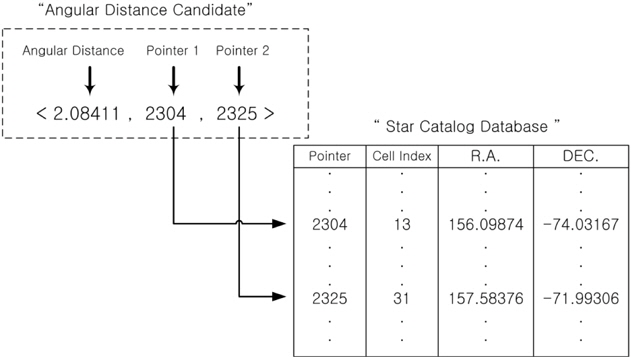
The proposed pivot algorithm uses pivot configurations as a basic identification pattern, thus, the way of configuring consistent candidate groups using pivots and verifying the candidate pivot groups, is the same as that of conventional pivot algorithms. However, this algorithm shows a difference in that it performs identification without using the apparent magnitude information which requires calibration. When pivot patterns are constructed between an arbitrary star and nearby stars, relatively large number of stars (at least more than 7 stars) are required to identify the pivot star without using the apparent magnitude. This results in the increase of identification time due to the increase in the number of searches and comparisons according to the number of stars. In order to resolve this issue, the relative brightness of stars, the orientation of brightness and the cell index which indicates the zone of the celestial sphere to which the star belongs, are used in the new pivot algorithm. The data of relative brightness of stars are used to identify the brightest star on a sensor image and then dimmer stars are identified using the cell indexes and the angular distances between the stars. The cell indexes to be used for the identification of relatively dimmer stars are the index of the cell to which the brightest star belongs and the indexes of cells surrounding this cell. The identification process of pivot pattern is as follows. A few bright stars are selected on a sensor image and using the brightest star as the center of pivot, a pivot pattern shown in Fig. 1 is constructed. In the next step, the angular distances between the pivot star and the dimmer stars are calculated from the geometrical relations of the star sensor and the candidates of angular distances which meet the angular distances are extracted from the database. In the identification algorithm which uses angular distances, the data are stored on a database in the order of [angular distance, Pointer 1, Pointer 2] generally and Pointer 1 and Pointer 2 represent the ID (Identification Number) of each star. And angular distances are used as indexes to obtain the segments of angular distance from the database. When the segments of the angular distance candidates comprising a pivot are determined, the pointer information entailing those candidates are compared to find a star which is common for all the candidates and it is identified as the pivot star. If the comparison is made only for the magnitude of angular distance, all of two pointers comprising an angular distance candidate should be compared, which is not efficient at all. If we remind that the pivot recognition begins from the brightest star, the brightest star could be found rather efficiently. As shown in Fig. 1, when the segments of angular distance are constructed between the brightest star and nearby stars, all the segments of angular distances have the orientation of brightness in addition to the magnitude and show the characteristics of vector. Therefore, arranging all the data of angular distances on the database according to the orientation of brightness could improve search speed. Between the two stars comprising an angular distance, if we designate the brighter one as i, and the dimmer one as j, it is sufficient to search and make a comparison for Pointer 1 only among the angular distance segments by arranging the data of the database as below in order to identify the brightest star.

[Angular distance, Pointer 1 (ID of i star), Pointer 2 (ID of j star) ]

The identification using the orientation of brightness is effective when the pivot star is bright enough compared to nearby stars. When the stars on a sensor image show similar brightness, the selection of pivot star becomes hard. In this case, the process of making each star as a center of pivot is repeated in the order of brightness, until the pivot star is identified. Then the identification time will be extended in proportion to the number of selections for a pivot star. Therefore, in order to avoid this kind of situation, there should be at least one star to show distinct brightness compared to the other stars within FOV (Field of View). The following equation can be used to find out the existence of a star bright enough within FOV (Liebe 2002).

N_FOV indicates the number of FOV in case the celestial sphere is divided by a circular FOV, and N_mag is the approximate number of stars which show magnitude brighter than a certain degree. For a star sensor sith 8° circular FOV which senses stars brighter than magnitude 6.0, the magnitude of about 4.5 could be set as a standard of enough brightness to show distinct brightness. For the configuration of this star sensor, the number of 8° circular FOV is calculated to be N_FOV=821 and the number of stars brighter than the magnitude of 4.5 is calculated to be N_mag=871. Thus, since there is at least one star wich shows the magnitude of 4.5 within the FOV, the star identification is possible while avoiding repeated steps of pivot star identification.

Cell index, a new identification information, is used to identify the other relatively dimmer stars. The cell index indicates the location of a cell when the celestial sphere is divided into zones of a fixed size and the size of cell is determined similar to the FOV size of a star sensor. All the stars on the celestial sphere belong to specific cells and the FOV of a star sensor consists of several cells. Thus, it is not necessary to search entire star catalog database but only requires searching for a small part of the database, which improves the star identification speed and reduces the possibility of wrong identification. The cell index of each star is calculated in advance and registered on the database for a later reference through a star pointer (or ID). The cell indexes to identify relatively dimmer stars are obtained from the brightest star identified already and adjacent stars. When the cell indexes are decided, the angular distance candidates are searched among the candidates which have the same cell index, the number of resulting candidates is very small or just one. The speed and the reliability of the rest dimmer star identification improve greatly due to this small count of candidates. The methodology to construct cells and to assign cell indexes is described in Section 3.

The identification of stars in a star sensor is a process of search and comparison between the star information which is obtained from the built-in star catalog and the one from a sensor image until those two are found to be identical. Hence, the performance of identification depends on search method, comparison method, and the status of optimization of the star catalog to be compared. In general, the optimization of a catalog is to choose minimum number of stars required for the identification of stars through the process such as the removal of adjacent stars, removal of superfluous stars in regions of high star density. The abridged catalog through optimization helps to improve the efficiency of the algorithm. The new star identification algorithm uses two databases for the mission databases. One of them is the angular distance database and the other is the catalog database. The representative source catalogs for the generation of mission database during the star identification are shown below.

SAO (Smithsonian Astrophysical Observatory star catalog) BSC (Yale Bright Star Catalog) SKY2000 Master star catalog

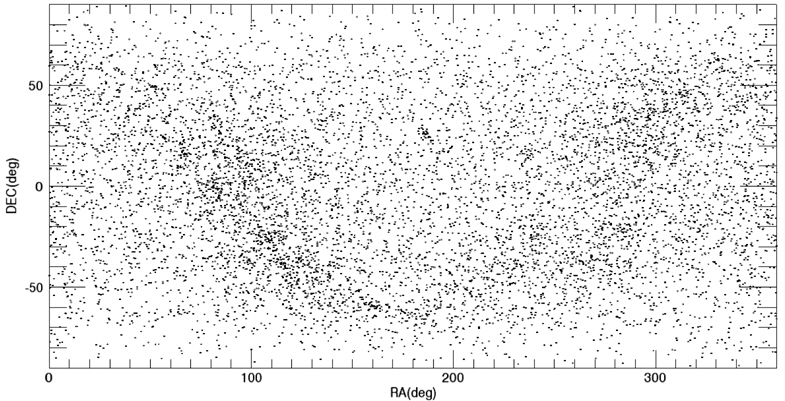
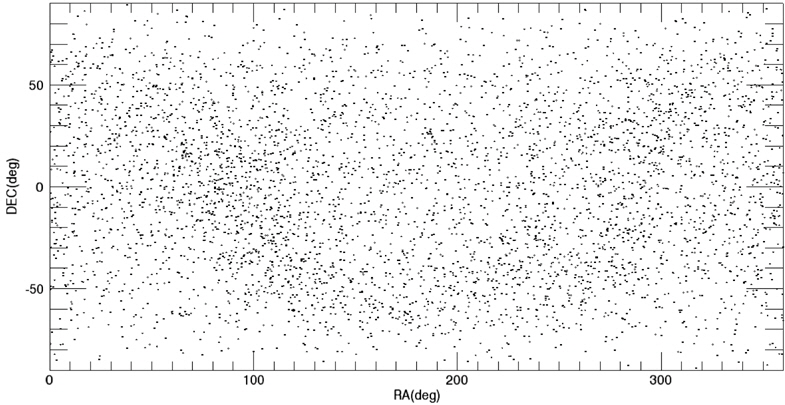
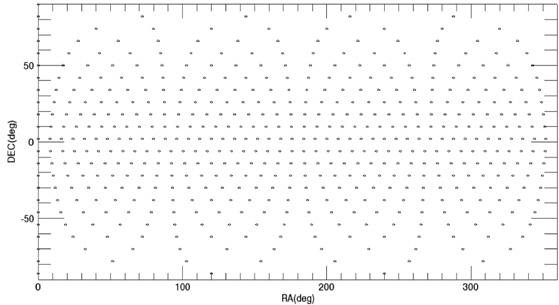
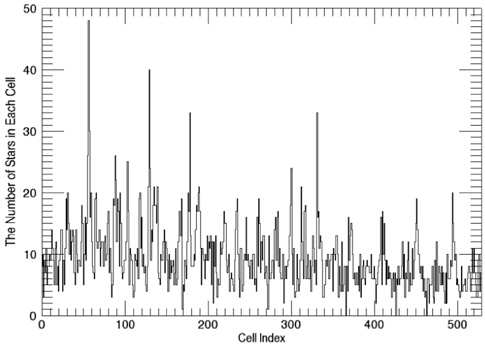
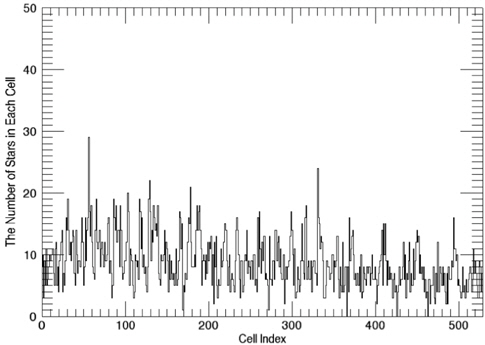
Among these catalogs, we selected the BSC (Yale Bright Star Catalog) as the source catalog for optimization. BSC includes information of the 9,110 celestial bodies with the brightness up to the magnitude of 7.0 (Hoffleit & Warren 1991). 14 of them are not stars (a nebula, a cluster), thus, these are removed first from the source catalog to construct the optimized catalog. The reference time of this catalog is J2000. For the generation of mission catalog databases, the apparent magnitude of 6.0 is set as a threshold value and the celestial sphere is divided into zones with the size of 8° circular FOV and 5 brightest stars are selected for each FOV. Fig. 2 shows the star distribution of the original source catalog and Fig. 3 shows star distribution of the optimized catalog with respect to 8° FOV. The number of stars in this figure is reduced to almost half the size of the original source catalog.

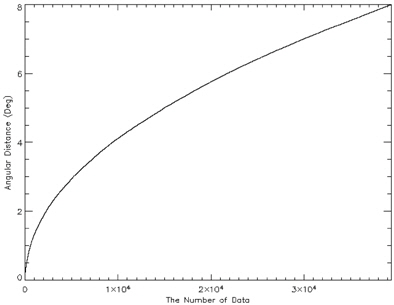
Once the optimized catalog is constructed, the next step is to generate the angular distance database comprised of angular distance and pointers of two stars composing the angular distance. The angular distances between two stars can be calculated easily using the coordinates of stars and they are sorted in an ascending order of angular distance in order to make the search process efficient. The star identification algorithm uses the binary search to find angular distances. The distribution of angular distances calculated between the stars are shown in Fig. 4. As described above, in order to embody the orientation of brightness effectively, the storage order of information on the angular distance database is arranged in the sequence of [angular distance, Pointer 1, Pointer 2]. Where, Pointer 1 indicates the brighter star among the two stars which forms an angular distance and Pointer 2 represents the other star which is relatively dimmer.

Cell index is an identification information and it is used to identify relatively dimmer stars. Cells are constructed by dividing the celestial sphere into zones of a fixed size and the location of a cell is designated as the cell index. All the stars on the celestial sphere belong to specific cells. Thus, when a star is identified, the cell information of the identified star and the surrounding cells could be obtained and the identification process is performed for the range of cell indexes figured out to enable the fast and reliable identification.

The methodology to divide the celestial sphere into fixed zones and to assign the cell index to each cell has been developed already (Bae & Schutz 2001). When the celestial sphere is divided by fixed sizes, the center of a cell is calculated using the following equations.

δ_n and α_nj indicates declination and right ascension, respeclively alld ε_n is defined as follows:

Where, N is determined by the cell size and the number of total cells and is calculated using the following equation.

In this equation, the symbol [ ]_f means the minimum integer which is less than or equal to the value in the brackets and the size of cell determined by N should be set greater than or equal to the FOV size of a star sensor to minimize the number of cells to compare during the identification process. Using the above equations, the celestial sphere is divided into N+1 declination zones and each declination zone is subdivided into (2n+1) subzones of uniform interval. Consequently, the celestial sphere is divided into (N+1)² cells without superposition. All the cells have the shape of trapezoid except the polar zones. Fig. 5 shows the distribution of cells on the celestial sphere with 8° FOV (N =22). The position of cell (cell index) is determined by the combinations of n² + j. Where, n and j are calculated from the following equations.

Whhere, the symbol, [ ]_c means the maximum integer which is greater than or equal to the value in the brackets. Δδ and Δα is the width of each cell. While the cell index can be written on a database, it can be calculated directly using the coordinates of a star when the available memory is limited. The number of stars counted in each cell from the source catalog and the optimized catalog are shown in Fig. 6 and Fig. 7 respectively. The structure of a database for the identification is depicted in Fig. 8.

The process of star identification based on the new algorithm is as follows. When star images are obtained from the star sensor, sufficient number of stars for the identification are selected. Selected stars are sorted in the order of brightness and each star is identified as a pivot star. Detailed processes are described as below. First of all, sufficient number of stars necessary for the identification are selected from the sensor image. At least three stars should be selected from the sensor image to identify stars using the pivot pattern. When sufficient number of stars which have an apparent magnitude over the threshold, are chosen from the star image, those are sorted in the order of brightness and registered on a sensor star list. From the sensor star list, stars necessary for the pivot identification are selected according to the rank of brightness to construct pivot patterns. The number of pivot members comprising pivot patterns is four or five including the pivot star. After pivot members are configured for a pivot, angular distances between the stars comprising the pivot are calculated. The angular distances obtained are expressed as Angular Distance Matrix (ADM) which represents pairs among them and it is referred to find the ID of pivot star from the angular distance database. In order to identify the brightest pivot star, the relative brightness and the orientation of stars are utilized. For each segment of angular distances between the pivot star and nearby stars, corresponding angular distance candidates are extracted from the angular distance database. Pointer 1 of those candidates are searched to find the pairs with the common specific ID, a new pivot group is constructed based on this ID. There could be several pivot groups and a validation test is performed for the groups whose sizes are greater than K-2, where K represents the number of members for a pivot pattern. Validation is performed by verifying the angular distances of adjacent stars as in the Match Group Algorithm. If the difference between the angular distance of adjacent stars from the sensor image and the angular distance registered on ADM is within the error range, the two are considered to show concurrence. Among the candidate groups with frequency of concurrence greater than a certain value, the pivot star of the pivot group with best concurrence is considered to be identified. However, if the pivot group with best concurrence is not unique, the identification of the pivot star of the group is considered to be a failure. The star identification using the orientation of brightness continues until the identification of the brightest star on the sensor star list is accomplished. Once a star in the star sensor list is identified, the second-step star identification is initiated using the cell index. Cell indexes could be referenced from the catalog database using the pointers of stars which belong to the identified pivot group. The number of cell indexes obtained ranges from one to four. The identification using the cell indexes is performed for the stars in the sensor star list.

As in the first step of identification, the selection of angular candidates from the angular distance database and the construction of pivot groups are performed for the pivot configuration with a new pivot star. The selection of angular distance candidates to construct a pivot group is performed for the angular distance candidates which have the same cell index as those obtained in the previous steps. The number of angular distance candidates obtained from the comparison of cell indexes is only one or very few. As a result, the constructed pivot group candidate is almost unique too. At this time, the orientation of brightness is not applicable anymore and both Pointer 1 and Pointer 2 of the angular distance candidate are searched to construct pivot groups. After the validation test for a constructed pivot groups is completed and when it is satisfied, the pivot star is considered to be identified. The pattern recognition using cell indexes are repeated until the dimmest star is identified.

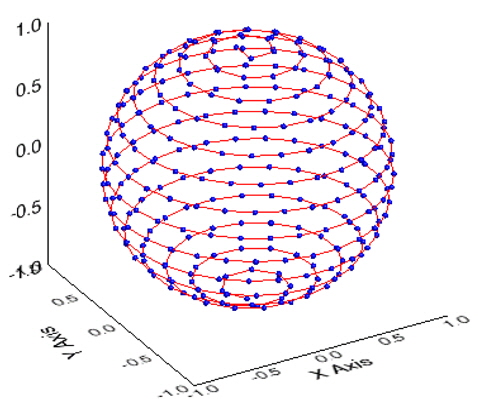
Validation was performed for the star identification algorithm with respect to the uniform direction on the celestial sphere. There are various methods to describe the position on the celestial sphere with uniform intervals and Spherical Spiral Method was used in this study. Fig. 9 indicates the uniform direction distribution based on Spherical Spiral Method. The n points of spherical spiral are represented by the unit vector, P_k’, on an orthogonal coordinate system using the following equations.

The validation of algorithm was performed for n=1000 and Fig. 10 shows the spherical spiral points for this case. Among these, the number of stars in FOV turned out to be less than 3 for 121 points and the success rate of identification was calculated excluding those points. The validation on the performance of identification was performed varying the angular distance error and the apparent magnitude error of standard deviation.

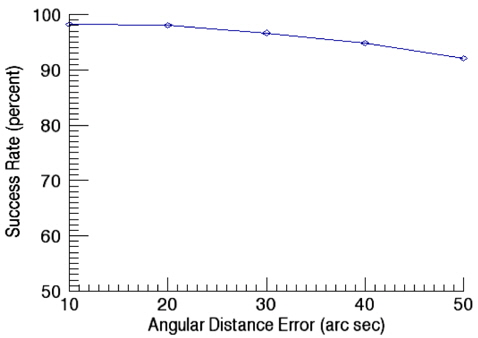
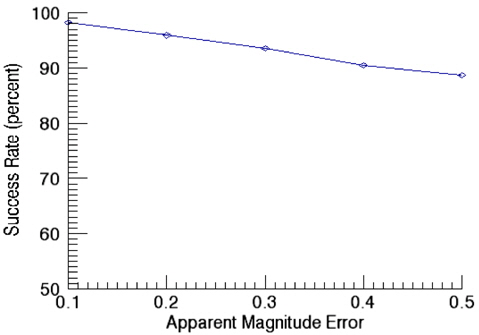
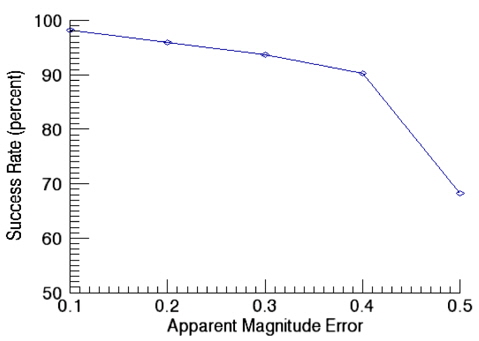
Fig. 11 shows success rates of star identification as a function of angular distance error. In this validation of performance on star identification, the apparent magnitude error is kept as 0.1. The results of identification show the success rate of 98.3% at the angular distance error of 10 arcsec while it is decreased to 92.2% at 50 arcsec as the error increases. The validation of the success rate as a function of apparent magnitude error was performed with the angular distance error of 10 arcsec and the results are shown in Fig. 12. As noises in the apparent magnitude increases, some stars on the catalog are not identified occasionally, or in some cases, stars not registered on the catalog are recognized. As the apparent magnitude error increases, the success rate of identification drops to 88.6 % for the apparent magnitude of 0.5.

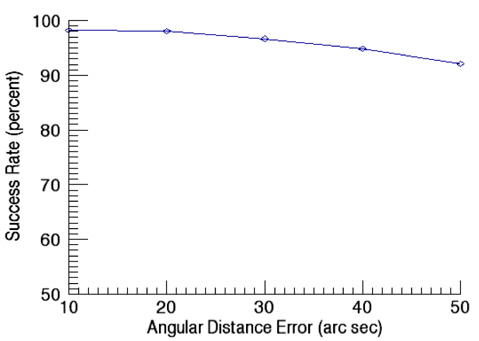
Match Group Algorithm which uses the apparent magnitude as an identification information, is a pivot star identification algorithm. Comparison was made between this algorithm and the newly developed algorithm. It is not easy to implement the Match Group Algorithm exactly same as the original, the implementation was performed as close as possible to the original. The algorithm was implemented according to the methodology of Van Bezooijen(1993) and Padgett(1997). The star catalog used in the identification is the same catalog obtained from the pivot algorithm developed. Firstly, the success rate of identification for Match Group Algorithm was calculated as a function of angular distance error and Fig. 13 shows the results. In this validation, the apparent magnitude error is kept as 0.1. As shown in Fig. 13, the success rate of identification is almost same as that of newly developed algorithm (Fig. 11). The reason why the two algorithms show similar success rate of identification for angular distance error is that both two algorithms use the pivot configuration which is basically the same pattern of identification, thus, the angular distance error is a dominant factor for the success rate with a fixed apparent magnitude. Secondly, the impact of the apparent magnitude error was examined for Match Group Algorithm and the results are shown in Fig. 14. After the comparison of the success rate of Match Group Algorithm (Fig. 14) with that of newly developed pivot algorithm (Fig. 12), we have found that the success rate shows very little change for small apparent magnitude error while the success rate drops rapidly for a relatively large error of 0.5. This result indicates that the current algorithm which uses the relative brightness of a star and the cell index, is less sensitive to the apparent magnitude error of a star than the Match Group Algorithm which uses the apparent magnitude information of each star.

A new star identification algorithm which utilizes pivot patterns not using the apparent magnitude information has been developed to eliminate the calibration of magnitude. This new star identification algorithm consists of two steps of recognition process. In the first step, the brightest star in a sensor image is identified using the orientation of brightness between two stars as a recognition information. In the second step, the cell index derived from the brightest star is used as a new recognition information to identify dimmer stars. When using the cell index information, searches are performed over a limited portion of the star catalog database to enable the faster identification of dimmer stars. Compared to the conventional pivot algorithm which uses the apparent magnitude information, the new pivot algorithm shows less sensitive characteristics to the apparent magnitude error. In order to utilize the apparent magnitude information, the calibration of magnitude is required, which is quite tricky. Also, there still is an uncertainty in the magnitude itself and the sensitivity of sensor degrades as time elapses to increase the uncertainty in magnitude information. However, the performance of star identification in the new pivot algorithm will not be degraded since it uses relative brightness of a star. Also, the new algorithm internally generates the cell index which specifies the zone of a star as an identification information. Therefore, if the cell index is used as a priori information, the spacecraft attitude information could be obtained faster and reliably to enable the continuous acquisition of the data.