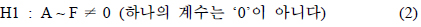In this study, regression equation was analyzed to estimate non-point source (NPS) pollutant loads in orchard area. Many factors affecting the runoff of NPS pollutant as precipitation, storm duration time, antecedent dry weather period, total runoff density, average storm intensity and average runoff intensity were used as independent variables, NPS pollutant was used as a dependent variable to estimate multiple regression equation. Based on the real measurement data from 2008 to 2012, we performed correlation analysis among the environmental variables related to the rainfall NPS pollutant runoff. Significance test was confirmed that T-P (R2=0.89) and BOD (R2=0.79) showed the highest similarity with the estimated regression equations according to the NPS pollutant followed by SS and T-N with good similarity (R2>0.5). In the case of regression equation to estimate the NPS pollutant loads, regression equations of multiplied independent variables by exponential function and the logarithmic function model represented optimum with the experimented value.
비점오염물질은 현재 호소 및 하천의 수질문제에 있어서 가장 중요한 이슈 중 하나로 떠올랐으며, 토지이용 특성이나 강우사상, 지역별 우수・오수 관리시스템 등 다양한 요인에 따라 발생정도가 다르다. 시간적・공간적 특성에 따른 발생오염물질의 정량화가 매우 어려우며, 점오염원에 비해 비교적 오염 농도는 낮지만 절대량이 크기 때문에 비점오염원에 대한 적정관리가 이루어지지 않고서는 수계환경개선 및 수질기준을 달성하기 어렵다(MOE, 1995). 이러한 비점오염물질은 강우와 함께 하천 및 호소로 유입되어 수질에 중요한 영향을 미친다(Bang et al., 1997, Bang et al., 2000, Kwun, 1998). 또한 비점오염원의 유출 현상은 강우 특성과 밀접한 관련을 가지고 있으며, 강우유출은 토지이용, 경사도, 식생, 강우강도, 강우량, 선행무강우일수 등에 따라 각기 다른 유출 특성을 보인다(Patrick, 2002). 그러므로 다양한 수문인자들 사이의 관계를 통하여 다중회귀식을 수립하는 것이 비점오염물질의 발생량을 예측하는데 신뢰도 및 상관도를 높일 수 있다. 그러나 이를 수행하기 위해서는 다중 상관관계 분석을 위한 인자별 입력 자료에 대한 다량의 수문자료가 필요하며, 기존 축적된 장기간 수문자료가 많지 않을 경우 다중회귀식이 일차회귀식보다 신뢰성이 떨어질 수 있다(Lee and Bae, 2002, MOE, 1995).
비점오염물질의 유출에 영향을 미치는 이러한 다양한 인자들의 영향으로 인해 비점오염물질 유출량 추정의 정량화를 위해서는 강우지속시간 동안의 정확한 유량과 수질에 대한 실측자료가 요구되고, 실측된 자료를 바탕으로 각 인자들 간의 영향정도 파악이 최우선적으로 실시되어야 한다.
본 연구에서는 과수재배지에서 유출되는 비점오염원부하량을 추정할 수 있는 회귀식을 도출하고자 하였다. 이를 위해 비점오염원 유출에 영향을 미치는 강우량, 총유출고, 평균시간당 강우량, 평균시간당 유출량, 선행무강우일수, 강우지속시간 등을 독립변수로 적용하고, 비점오염원을 종속변수로 하여 다중회귀식을 적용하였다. 2008년부터 2012년까지 실측된 값을 기초 자료로 하여, 강우 시 비점오염원의 유출에 관련된 변수들의 상관성 분석을 수행하였다. 아울러 강우-유출에 영향을 미치는 유출 변수를 선형 및 선형변환모델에 적용하여 적정성을 검토하였으며, 비점오염원별 유출부하량 추정 회귀식을 도출하여 실측이 어려운 다양한 강우조건에 대해 유출부하량을 산정하였다. 향후 이러한 경험식을 바탕으로 현장 실측이 어려운 유역에 대한 비점오염원 부하량 산정 및 비점오염원 관리를 위한 기초자료를 제공하고자 하였다.
비점오염원 모니터링을 수행하기 위한 대상 지점은 낙동강 수계 내에 위치하고, 조사대상 과수의 주 재배지가 속하는 지역을 선정하였다. 과수 선정은 낙동강수계의 토지이용 현황 중 과수원 분포 현황 분석을 통해 재배 비율이 높은 과수를 선정하였다. 또한 강우 시 측정이 용이한 지점을 조사대상 지점으로 하여 강우 시 모니터링을 수행하였다. 선정된 과수는 포도, 배, 사과이며, 포도재배지의 경우 경상북도 경주시 건천읍에 위치하고 있으며, 조사의 효율성을 높이기 위해 근교 2곳을 조사 대상지로 선정하였다. 재배지 면적은 각각 2000 m2, 1800 m2 이다. 배재배지는 경상북도 상주시 사벌면에 위치하고 있으며, 면적은 각각 1943 m2, 2484 m2 이다. 사과재배지는 경상남도 합천에 위치하고 있으며, 조사대상 지점 면적은 864 m2 이다.
선정된 세부 토지피복 지점은 연차별 간격을 두어 모니터링을 수행하였으며, 2008년부터 2009년까지는 포도재배지, 2010년에서 2012년까지는 배재배지, 2012년에는 사과재배지에 대해 강우 시 비점오염원 유출에 대한 모니터링을 수행하였다. 포도재배지는 모니터링 기간 동안 총 51회의 강우사상에 대한 모니터링을 수행하였으며, 이 중 유출이 발생한 횟수는 총 19회 이다. 배재배지는 총 48회의 모니터링 중 13회의 강우사상에서 유출이 발생하였다. 사과재배지는 총 16회의 모니터링 중 7회의 강우사상에서 유출이 발생하였다.
강우에 따라 발생되는 비점오염원 유출수에 대한 모니터링을 위해, 각각의 조사지점에 강우강도계 및 유량계를 설치하여 조사대상지점에서 일어나는 강우 형태에 따른 유출수의 변화를 살펴보았다. 실측에 사용된 강우강도계는 Tipping Bucket Mechanism 방식의 호주 Environdata Environmental Monitoring & Management 사의 RG-20으로 1분 단위의 강우량 측정이 가능하다. 유량계의 경우 비만관 전자식 유량계로 미국 MARSH McBIRNEY 사의 Flo-Tote3로 1분 단위의 유량측정이 가능하다. 조사대상지점에 대한 유량계의 설치는 최종 유출구에 설치하여 외부로부터 강우유출수의 유입이 없는 상황에서 유출량을 조사하였다. 시료 채취 및 분석의 경우 국립환경과학원에서 개정된 ‘강우 유출수 조사방법’에 준하였고, 강우량 및 유출량의 경우 현장조사를 원칙으로 하였고, 불가할 시 가장 근접한 기상청 자료를 활용하였다(NIER, 2007). 채수 시료에 대한 항목별 분석방법은 Table 1에 나타내었다.
[Table 1.] Analyzed items and analysis methods

Analyzed items and analysis methods
비점오염원은 강우 및 유출 관련 인자와 밀접한 관련성이 있으며, 강우 유출은 토지이용, 경사도, 식생, 강우강도 등에 따라서도 큰 차이를 보인다. 또한 각 지역의 지형, 수리・수문 조건 및 토지이용현황, 강우특성 등 다양한 요인에 따라 배출특성이 매우 다양하게 나타난다. 따라서 비점오염원의 정량화를 위해서는 강우지속시간 동안의 정확한 유량과 수질에 대한 실측자료가 요구되고, 실측된 자료를 바탕으로 각 인자들 간의 영향정도 파악이 우선시 되어야 한다(Management Committee of Nakdong River Basin, 2010).
본 연구에서는 과수재배지의 강우 유출수 모니터링 결과를 활용하여 비점오염원 유출과 밀접한 관련이 있는 다양한 변수들과의 상관성 분석을 통해 변수들 간의 영향정도에 대한 우선순위를 부여 하였다. 모니터링 결과 중 비점오염원 부하량을 산정할 수 있는 유출이 발생된 강우사상에 대해서만 상관성 분석을 수행하였다.
수질항목별 비점오염원 유출부하량과 독립변수들 간의 상관관계 분석은 통계분석 시 주로 활용되는 SPSS(statistical package for the social science)를 사용 하였으며, 상관계수는 Pearson 상관계수를 사용하였고, 각 변수들은 정규분포를 따른다는 가정을 하였다. 상관계수 값의 범위는 -1부터 +1까지 이며, 계수의 부호는 관계의 방향을 가리키고 절대값은 관계의 강도를 나타낸다.
유의성 검정은 양측검증으로 하였고, 유의한 상관계수에 대해서는 별표시를 하였으며, 1개의 별 표시는 0.05 수준에서 유의한 상관계수를 나타내며, 2개의 별 표시는 0.01 수준에서 유의한 상관계수이다. 오염물질별 각 변수들에 대한 상관성 분석 시 결정계수 50%이상, 유의확률 95%이상에 해당하는 항목만을 선택하여 선형 및 선형변환모델에 적용하는 인자로 선택하였다.
비점오염물질 유출량은 강우량, 유출량, 강우강도, 선행무 강우일수, 강우지속시간 등 다양한 수리・수문 인자들과 복합적으로 연관되어있다. 그러므로 다양한 수문인자들 사이의 관계를 통하여 다중회귀식을 수립하는 것이 비점오염물질의 발생량을 예측하는데 신뢰도 및 상관도를 높일 수 있다. 그러나 이를 수행하기 위해서는 다중 상관관계 분석을 위한 인자별 입력 자료에 대한 다량의 수문자료가 필요하다(Yoon et al., 2010).
본 연구에서는 2008년 ~ 2012년까지 과수재배지에서 실측된 값을 근거 자료로 하여, 강우 시 비점오염물질의 유출에 관련된 변수들의 상관성 분석을 통해 우선순위를 부여하였다. 선정된 변수를 선형 및 선형변환 식에 적용하여 적정성을 검토하였으며, 오염물질별 최적 모델을 제시하였다.
회귀식의 선정은 결정계수와 유의 확률 값을 기준으로 하였고, 동일한 오염물에 대해 2-3개의 회귀식이 비슷한 R2 값을 가질 때는 각각의 독립변수 중 정확한 자료획득가능성을 고려해서 입력변수가 적은 회귀식을 선택하였다. 유의도가 없는 독립변수들이 존재하거나 다중 공선성의 존재여부를 검토한 후 변수는 취사선택 하였다. 다중 공선성의 검토는 독립변수간의 상관계수가 높을 경우 변수전체를 포함한 회귀식은 다중공선성을 의심하였으며, 분산분석표에서 모델의 적합성을 나타내는 F 값과 R2 이 높음에도 각 독립변수에 대한 모수추정치의 결과를 비교해 유의한 변수를 선택하였다.
유의성 검증은 종속변수(P)와 독립변수(Xi)간에 선형관계를 규명하는 검증으로 귀무가설(H0)와 대립가설(H1)을 설정하여 귀무가설이 기각되면 종속변수 중 적어도 하나는 영향을 미친다는 것을 의미한다.
귀무가설의 검증방법으로는 F-검정을 이용하였고, 귀무가설이 기각되어 선형관계가 검정되면 각 회귀계수에 대해 t-검정을 이용하여 유의성 검정을 하였다. F와 t-검정 결과, P-값이 0.01(1% 유의수준)보다 작으면 매우 유의한 수준으로, 0.01과 0.15사이에 있으면 보통 유의한 수준, 0.15보다 크면 유의하지 않은 것으로 판정한다. 본 연구에서는 P<0.15 수준에서 의미가 있는 것만 선택하였다.
2.4.1. 입력 변수
회귀식은 당초 실측한 자료를 검정한 후 미계측 수계의 오염부하량 추정에 사용하기 위해 개발 되었으나, 최근에는 우수유출량, 단일 강우사상의 오염물 유출량 또는 평균농도, 계절별 평균 오염농도, 연간오염물 유출량 등을 이끌어내기 위해 많이 이용하고 있다. 이와 같은 모델에서는 토지이용만으로 비점오염량을 예측하는 것은 정확하지가 않기 때문에 비점오염원과 관련이 있는 자료를 유역조사에서 수집하여 모델의 독립변수로 사용해야 한다(MOE, 1995).
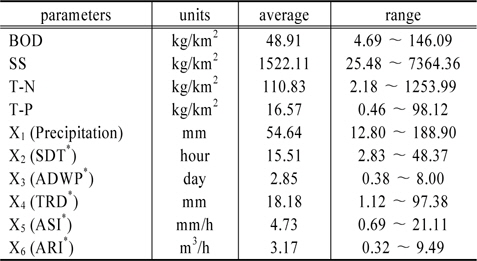
각각의 변수들에 대한 평균치 및 범위는 Table 2에 나타내었다. 비점오염원별 유출부하량 추정을 위한 독립변수로는 강우량(X1), 강우지속시간(X2), 선행무강우일수(X3), 총 유출고(X4), 평균시간당 강우량(X5), 평균시간당 유출량(X6)을 사용하였다. 종속변수는 비점오염물질별 유출부하량 값을 활용하였으며, 독립 및 종속 변수로 활용된 자료는 2008년부터 2012년까지 과수재배지에 대한 모니터링 결과를 활용하였다.
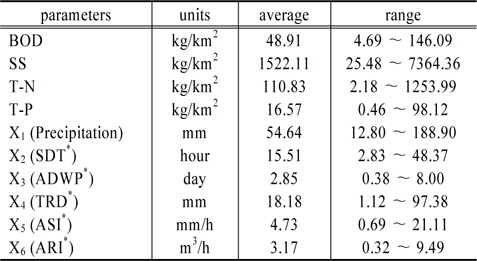
List of the selected parameters and hydrologic description of stormwater runoff sampled (2008∼2012)
2.4.2. 선형 및 비선형 회귀식
최적의 비점오염원 부하량 예측식을 만들기 위해서는 바람직한 식의 형태를 선정해야 하며, 이를 위한 기준 값은 결정계수(R2)이다. 적용된 선형 및 비선형 회귀식은 기존 연구자들에 의해 제시 및 활용되고 있는 식(MOE, 1995)과 본연구에서 제안한 식을 활용하였다. 활용된 식은 Table 3에 제시하였으며, 각각의 식에 상관성 분석을 통해 선정된 변수들을 적용하여 산정된 식의 결정계수 및 유의확률을 비교하여 비점오염원별 식을 선정하였다. 동일 오염물질에 대해 2-3개의 회귀식이 유사한 결정계수를 나타낼 때는 각각의 독립변수 중 정확한 자료의 획득 가능성을 고려하여 독립변수를 정해야 하기 때문에 입력변수가 적은 식을 선정하였다.
[Table 3.] List of linear and non-linear correlation equations for analysis

List of linear and non-linear correlation equations for analysis
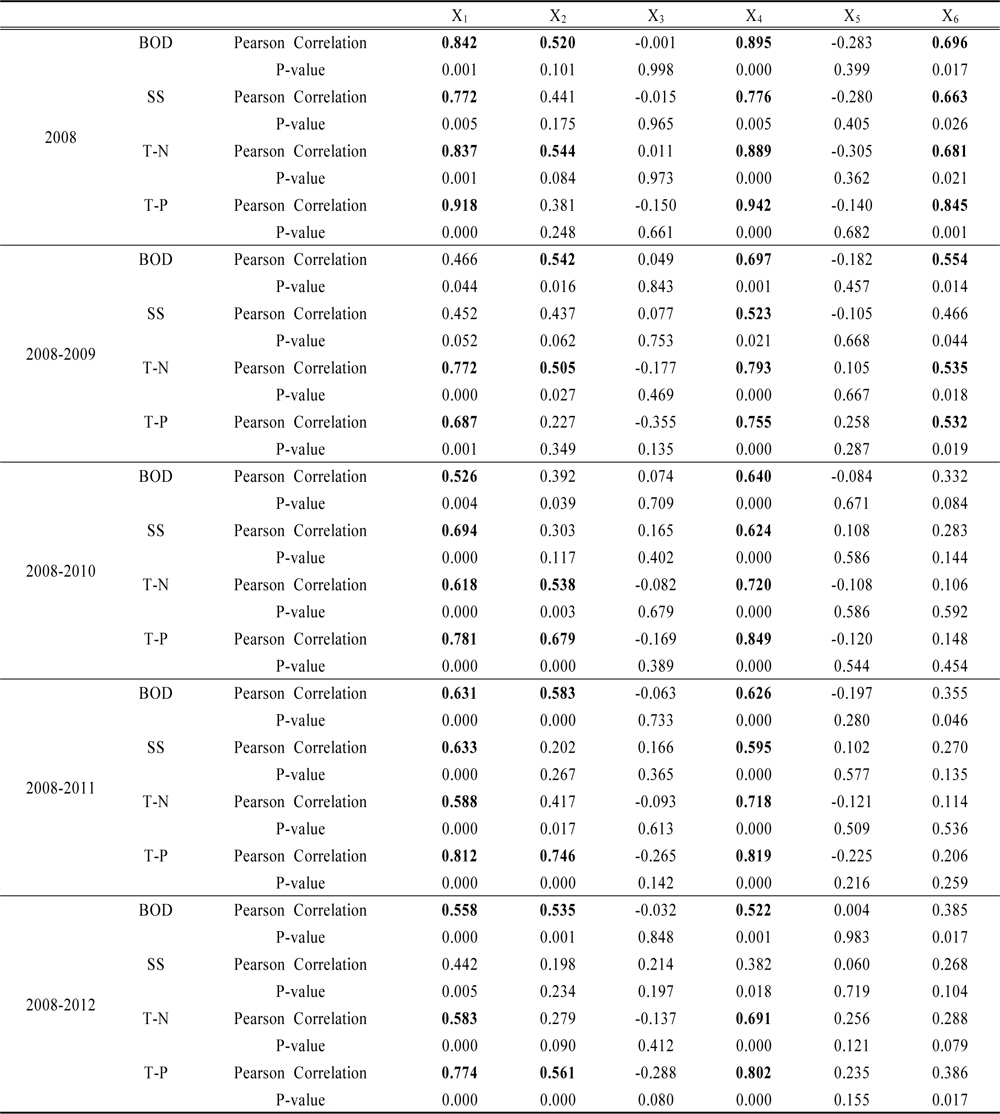
비점오염원별 유출부하량에 영향을 미치는 독립변수로 선택한 강우량, 강우지속시간, 선행무강우일수, 총유출고, 평균시간당 강우량, 평균시간당 유출량과 종속변수로 선택한 BOD, SS, T-N, T-P 유출부하량의 상관성 분석결과를 Table 4에 수록하였다. 상관성 분석은 조사 기간별 수집된 결과를 구분하여 분석을 수행하였으며, 모니터링 자료가 많아질수록 영향도가 높은 변수들의 차이를 확인하였다(Table 5). 2008년 모니터링에 대한 상관성 분석 결과는 강우량, 총유출고 및 평균시간당 유출고의 영향정도가 높게 조사되었으며, 강우지속시간의 경우 BOD와 T-N 유출부하량에도 영향을 미치는 것으로 나타났다. 독립변수별 영향정도는 총유출고>강우량>평균시간당 유출량 순으로 조사되었다. 2008년부터 2009년 모니터링에 대한 상관성 분석 결과는 총유출고의 영향정도가 높게 나타났으며, 독립변수별 영향정도는 총유출고>강우량>평균시간당 유출량>강우지속시간으로 조사되었다. 이후 조사기간을 2012년까지 추가하여 상관성 분석을 수행한 결과 과수재배지에서의 비점오염원 유출부하량에 대한 독립변수의 영향정도는 강우량과 총유출고의 영향정도가 높게 조사되었고, 강우지속시간도 일부 항목에 영향을 미치는 것으로 조사되었다.
[Table 4.] Correlation matrix of selected parameters and nonpoint sources
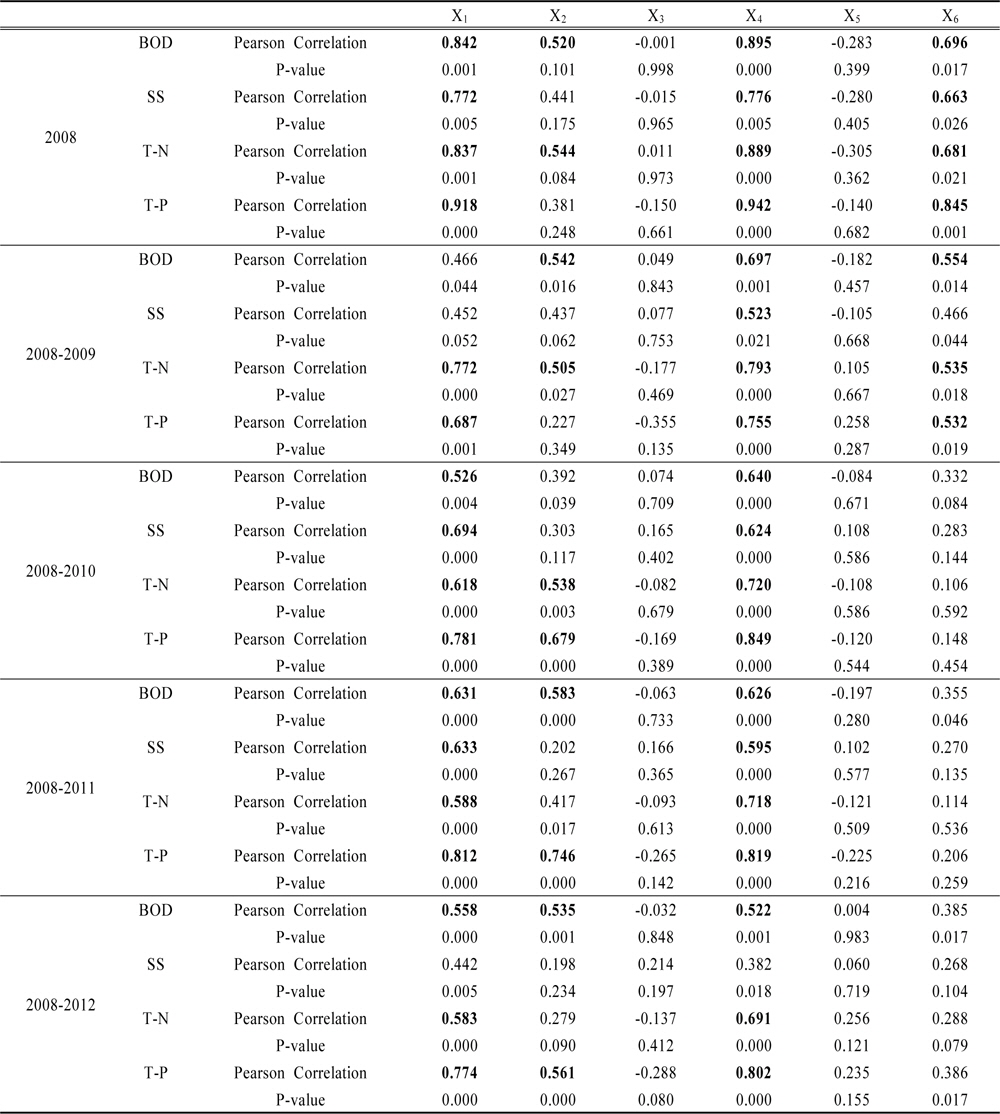
Correlation matrix of selected parameters and nonpoint sources
[Table 5.] Priority of the influential parameters to nonpoint sources load

Priority of the influential parameters to nonpoint sources load
2008년부터 2012년까지의 결과를 정리하여 비점오염원별 영향을 미치는 변수를 구분하여 보면, BOD : 강우량(R2=0.558) > 강우지속시간(R2=0.535) > 총유출고(R2=0.522), T-N : 총유출고(R2=0.691) > 강우량(R2=0.583), T-P : 총유출고(R2=0.802) > 강우량(R2=0.774) > 강우지속시간(R2=0.561)로 조사되었다. BOD 항목의 경우 강우량 및 강우지속시간의 영향도가 총유출고에 비해 높게 조사되었는데, 이는 조사지점의 토지피복이 투수성으로 되어있어 기저유출의 영향으로 인해 나타난 결과로 판단된다. 본 조사의 경우 표면 유출을 중심으로 모니터링을 실시하였으나, 조사지점의 투수성 토지피복 특성상 발생되는 기저유출수도 시료에 포함되게 된다. SS 및 영양염류항목의 경우 표면에 살포되거나 산재된 물질이 유출수에 포함되어 BOD 항목과는 다소 차이를 보여 주었다. SS의 경우 2011년 모니터링까지는 종속변수와 독립변수간의 상관성이 조사되었으나, 2012년 모니터링 결과를 추가하여 분석해 본 결과 상관계수가 50%이상으로 조사된 변수는 나타나지 않았다. 하지만 종속변수 중 강우량과 총유출고가 각각 0.442, 0.382로 상관계수를 보였으며, 이 결과는 2011년까지의 상관성 분석 결과와 같은 변수의 영향을 받고 있는 것으로 조사 되었다. 이에 따라 SS항목은 2011년까지의 상관성 분석 결과에 따라 종속변수를 적용하여 기타 항목과 같이 다중회귀식을 도출하였다.
연차별 모니터링 자료에 대한 상관성 분석을 수행하여 비점오염원 유출부하량에 영향을 미치는 변수들에 대한 우선순위를 도출하였다. 오염물질별(수질항목) 유출에 영향을 미치는 6개의 독립변수들 중 상관계수 50%이상, 유의확률 95% 이상에 해당하는 강우량, 강우지속시간, 총유출고, 평균시간당 유출량 등 4개의 변수들을 우선 적으로 각 수질항목별 비점유출량 추정 모델식의 독립변수의 후보군으로 선택하였다.
상관성 분석 결과, 상관성이 높게 평가된 변수들을 선형 및 비선형 회귀식에 적용하여 유의성을 평가하였다(Table 6). 각 변수들 간의 상관성 분석 결과 초기에 선정하였던 6개의 독립변수 중 강우량, 강우지속시간, 총유출고, 평균시간당 유출량이 비점오염물질의 유출부하량과 상관성이 높게 나타났다. 선정된 변수의 경우 BOD, SS, T-N, T-P의 경우 유사한 변수들에 의한 영향을 받는 것으로 조사 되었다. 선정된 변수에 대해 선형 및 선형 변형식에 적용한 결과 R2 와 adjR2 의 차이가 낮게 조사되었는데 수정된 R2 값의 경우 연구자가 세운 모델이 얼마나 일반성을 가정하고 합리적인지를 R2 값과의 비교를 통해 알 수 있는데, BOD의 경우 그 차이가 0.01로서 수정되었을 경우 1%의 변산이 줄어들었다. 나머지 항목들도 1-6%까지 변산이 줄어드는 것으로 조사되었다.
[Table 6.] Correlation analysis application result
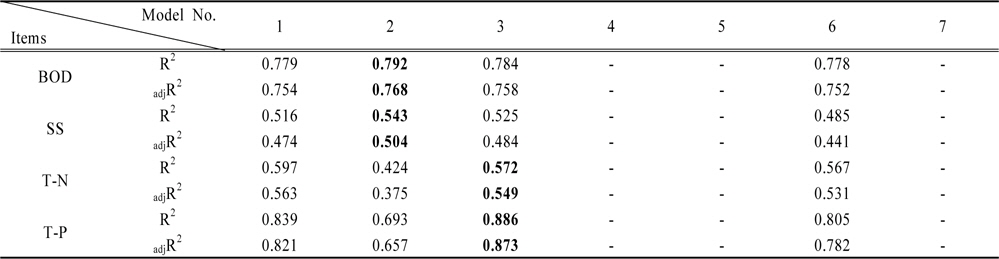
Correlation analysis application result
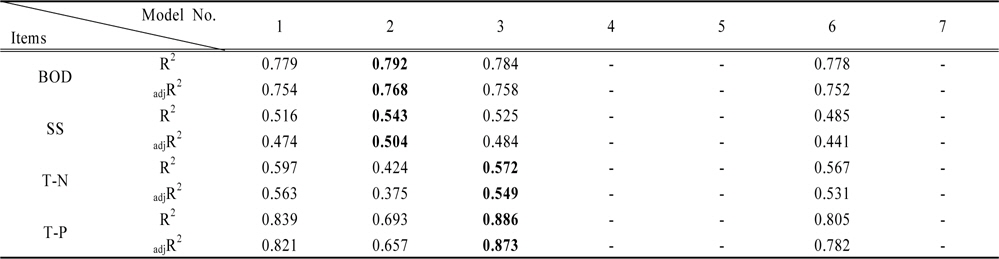
BOD 부하량의 경우 Model 2에 적용하였을 때 결정계수가 0.792로 조사되어 가장 높은 유의성을 나타내었고, Model 3의 경우도 0.784로 유의성이 높게 조사되었다. T-N의 경우 Model 1의 결정계수가 0.597로 높게 조사되었으나, 적용된식의 정규분포 검증에서 실패하여 다음으로 결정계수가 높은 3번식을 적용하여 식을 도출하였다. T-P의 경우 Model 3이 0.886로 조사되어 항목별 적용된 식들의 유의성을 확인할 수 있었다. SS의 경우 2011년까지의 모니터링 결과를 바탕으로 분석된 변수들을 적용해 본 결과 Model 2에 적용하였을 때 결정계수가 0.543으로 조사되었다.
적용된 회귀식들 중 Model 4, 5, 7의 경우, 변형된 회귀식으로 변수들 중 변형된 변수가 포함되지 않은 경우 기존 Model 1, 2, 3과 같은 형태를 나타내게 된다. 본 연구에서 적용된 변수들의 경우 변형 식에 해당하는 변수들은 상관성 분석에서 낮은 상관도를 나타내어 제외 되고, 해당 식의 적합성 평가가 이루어지지 않았다. 하지만 연차별 자료에 따라 해당 변형 변수의 상관성도 확인되고 있고, 향후 추가되는 모니터링 자료들에 대한 불확실성이 높아 다양한 변형 식에 대한 검토가 필요하여 본 연구에서도 삽입하여 적용해 보았다.
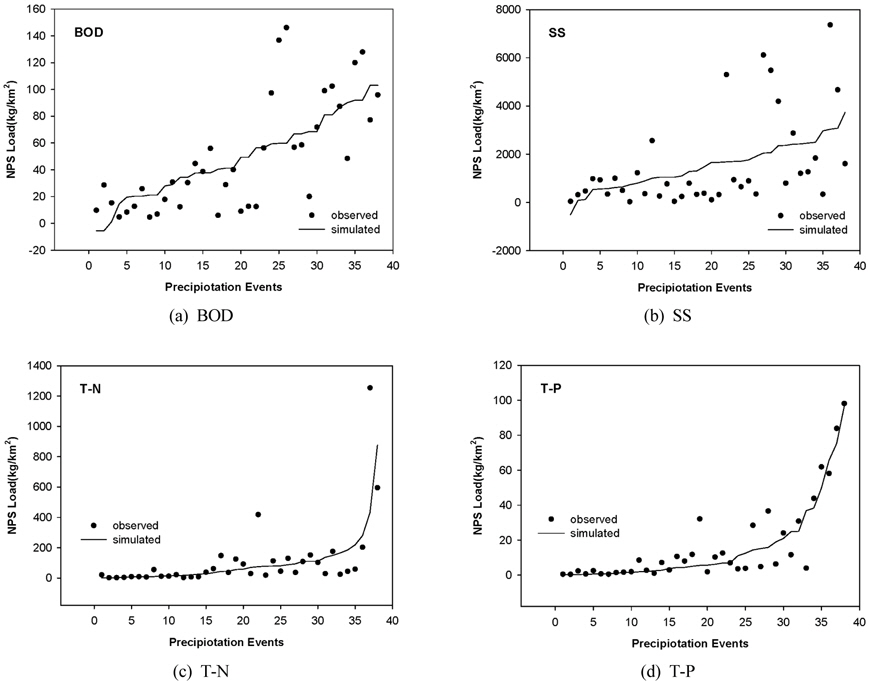
5년간에 걸쳐 측정된 강우량, 선행무강우일수, 강우지속시간, 총유출고, 평균시간당 유출량, 강우강도, 유출량 자료를 활용하여 이들 변수와 비점오염물질 별 유출부하량과의 통계분석을 통해 비점오염물질 별 유출부하량에 영향을 미치는 변수들의 영향 정도를 도출하였다. 유출에 미치는 영향정도가 큰 변수들을 활용하여 비점오염물질별 유출부하량 추정 회귀식을 제시하였다(Table 7). 비점오염원별 도출된 회귀식을 살펴보면, T-P의 경우 결정계수가 0.89로 가장 높은 유의성을 나타내었으며, BOD 항목 또한 0.79의 결정계수로 산정되어 높은 유의성을 나타내는 것으로 조사되었다. 나머지 SS와 T-N의 경우도 0.5이상의 결정계수를 나타내어 추정된 식의 유의성을 확인할 수 있었다. 유기성 오염물 지표로 적용될 수 있는 BOD와 SS 항목의 경우 독립변수들을 로그함수의 곱으로 표현한 Model 3의 유의성이 높게 조사되었고, 대표적인 영양염류의 지표인 T-N과 T-P의 경우 지수함수의 곱으로 복합적인 영향을 반영한 Model 3의 유의성이 높게 조사되었다.
[Table 7.] Selected models and correlation coefficient

Selected models and correlation coefficient
현재의 결과는 39회 현장 측정 자료를 이용하여 수행하였지만, 도출된 식의 신뢰도 향상을 위해 지속적으로 실측결과를 추가 할 계획이며, 아울러 지목을 확대하여 비점오염물질 유출부하량 추정 회귀식의 일반화를 동시에 추구할 예정이다.
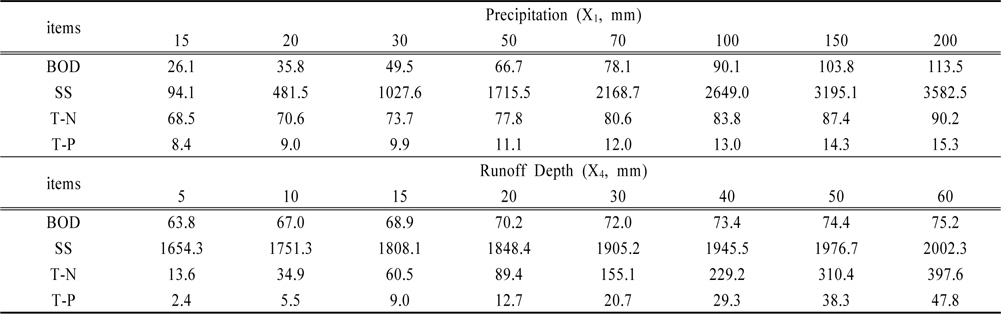
비점오염원별 도출된 회귀식에 포함된 변수 중 BOD, SS, T-N 및 T-P항목 회귀식 모두에 적용되고 있는 X1 (강우량), X4 (총유출고) 항목의 수치를 변화시키며 부하량을 추정하였다(Table 8, Fig. 2). 임의 변화 시키는 변수외의 다른 변수에는 해당 변수의 모니터링 평균값을 입력치로 고정시켜 입력 변수의 변화에 따른 유출부하량 변화를 추정하였다.
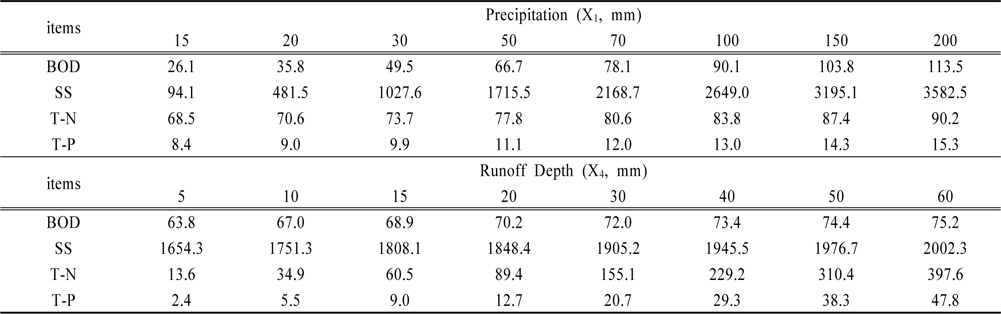
Stormwater runoff loads estimation according to precipitation and total runoff depth changes
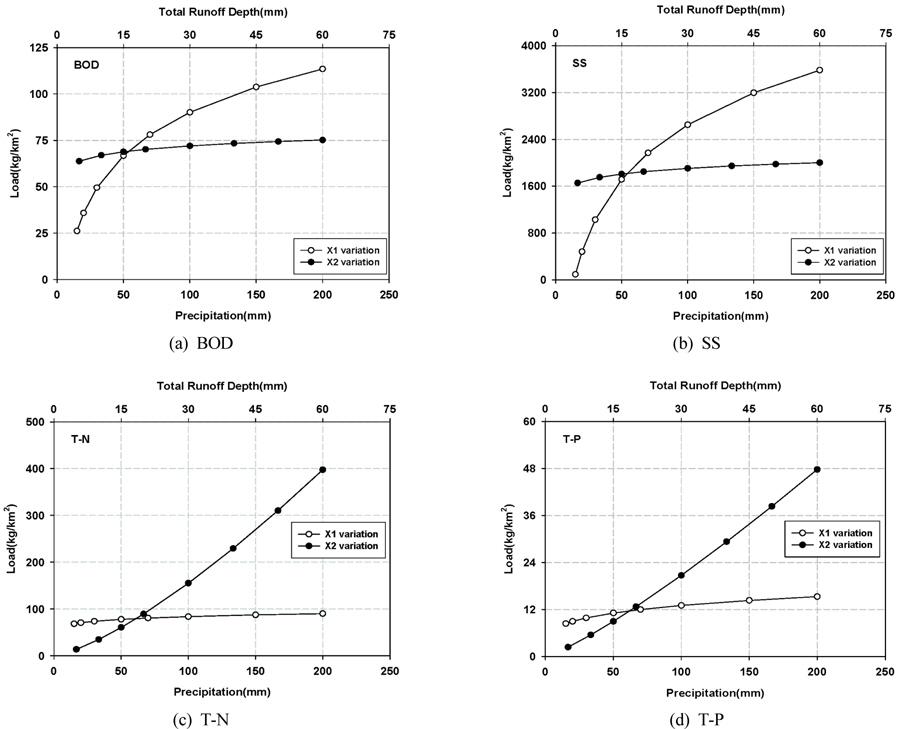
X1 (강우량)의 변화가 비점오염원의 유출에 미치는 영향을 분석하기 위하여 강우량 범위를 10-200 mm 까지 변화시키면서 비점오염원별 유출부하량의 변화를 관찰하였다. 강우량이 증가함에 따라 수질항목별 비점오염물질 유출부하량은 증가하는 경향을 보였지만 증가하는 정도는 수질항목별로 큰 차이를 보였다. 특히 BOD, SS의 경우 강우량의 변화에 대해 민감하게 반응하였으며, 강우량 15 mm 일 때 BOD와 SS의 유출부하량은 각각 26.1 kg/km2, 94.1 kg/km2인 반면 강우량이 10배 증가된 150 mm 일 때 BOD 및 SS가 103.8 kg/km2, 3195.1 kg/km2으로 BOD 4배, SS 34배 증가하는 결과를 보였다. 반면 T-N과 T-P의 경우 15 mm 에서 각각 68.5, 8.4 kg/km2인 반면 강우량 150 mm 에서 각각 T-N 87.4 kg/km2, T-P 14.3 kg/km2의 값으로 T-N 1.3배, T-P 1.7배 증가하여 강우량에 대한 민감도가 낮게 조사되었다.
총유출고 변화가 비점오염원별 유출에 미치는 영향을 살펴보기 위해 총 유출고의 값을 5-60 mm 까지 변화시키면서 유출부하량을 분석한 결과 강우량의 변화와는 상반되는 결과를 나타내었다. 총유출고를 5 mm 에서 50 mm 로 10배 증가시킬 경우 BOD는 63.8 kg/km2 에서 74.4 kg/km2 으로 1.2배 증가하였으며, SS의 경우 5 mm에서 유출부하량 1654.3 kg/km2, 총 유출고를 10배 증가시킨 50 mm 에서 1976.7 kg/km2로 1.2배 증가하였다. 반면 T-N의 경우 13.6 kg/km2에서 310.4 kg/km2로 23배가량 증가하였고, T-P의 경우 2.4 kg/km2 에서 38.3 kg/km2 로 16배가량 증가하여, 강우량 변화에 따라서는 BOD, SS 항목의 변화폭이 큰 것으로 조사되었으나, 총유출고의 변화에 따라서는 T-N, T-P 항목의 변화폭이 크게 조사되었다.
유역에 대한 수질관리를 위해서 점오염원뿐만 아니라 비점오염원에 대한 토지이용별 유출부하량 산정이 수행되어야 하며, 정확한 유출부하량 산정을 위해서는 장기적인 현장 모니터링을 통해 기초 자료를 축적하여야 한다. 이를 위해 2008년에서 2012년까지 5년간에 걸쳐 토지피복지도 중분류에 해당하는 과수재배지에 대해 강우 시 비점오염원 유출에 대해 장기 모니터링을 실시하였다. 모니터링을 통해 축적된 실측자료를 바탕으로 비점오염물질 유출에 직접적인 영향을 미치는 강우량, 강우강도, 강우지속시간 등의 자료를 독립변수로 하여 BOD, SS, T-N, T-P에 대한 유출부하량을 추정할 수 있는 수학적인 회귀식을 제시하였다. 분석된 결론을 아래와 같이 정리하였다.
1) 강우 및 유출관련 수리・수문학적인 인자의 비점오염원 유출에 미치는 영향정도를 분석한 결과, BOD와 T-P의 경우 강우량, 강우지속시간 및 총유출고에 민감하게 반응하였으며, SS와 T-N은 강우량과 총유출고의 영향을 받았다. 2) 비점오염원별 영향을 미치는 변수는 BOD : 강우량(R2 = 0.558) > 강우지속시간(R2 = 0.535) > 총유출고(R2 = 0.522), T-N : 총유출고(R2 = 0.691) > 강우량(R2 = 0.583), T-P : 총유출고(R2 = 0.802) > 강우량(R2 = 0.774) > 강우지속시간(R2 = 0.561)로 조사되었다. 3) 상관성 분석 결과, 초기에 선정하였던 6개의 독립변수 중 강우량, 강우지속시간, 총유출고, 평균시간당 유출량이 비점오염물질의 유출부하량과 상관성이 높게 나타났다. 4) 비점오염원별 추정된 회귀식은 T-P의 경우 결정계수가 0.89로 가장 높은 유의성을 나타내었으며, BOD 항목 또한 0.79의 결정계수로 산정되어 높은 유의성을 나타내는 것으로 조사되었다. 나머지 SS와 T-N의 경우도 0.5이상의 결정계수를 나타내어 추정된 식의 유의성을 확인할 수 있었다. 5) 본 연구에서 적용된 비점유출부하량 추정 회귀식의 경우 독립변수들을 지수함수의 곱으로 하여 복합적인 영향을 반영한 회귀식과 로그함수를 조화시킨 회귀식이 실측치를 잘 대변하였다. 6) 추정 회귀식을 활용하여 독립변수의 변화에 따른 비점오염원 유출부하량의 변화를 살펴본 결과, X1(강우량) 변화에 따라서는 BOD, SS 항목의 변화폭이 큰 것으로 조사되었으나, X4(총유출고)의 변화에 따라서는 T-N, T-P 항목의 변화폭이 크게 조사되었다.
본 연구와 같이 비점오염원 유출부하량을 정량적으로 추정할 수 있는 회귀식 검증을 통해, 식에 포함되어 있는 유출 변수의 변화 따른 비점오염물질의 유출 특성을 파악 할 수 있다. 이러한 결과를 바탕으로 비점오염원 최적관리를 위한 구조적시설을 설치할 때 시설의 부피, 적정처리시간, 처리율 등에 대한 종합적인 정보를 제공할 수 있을 것으로 기대된다.