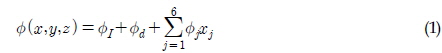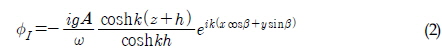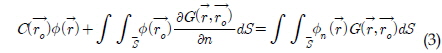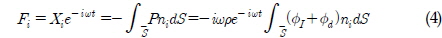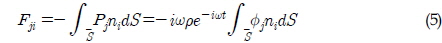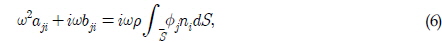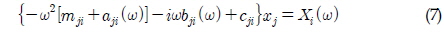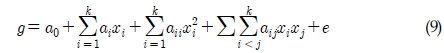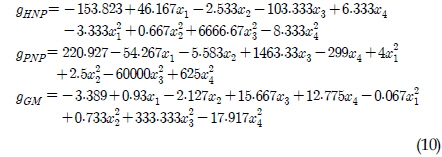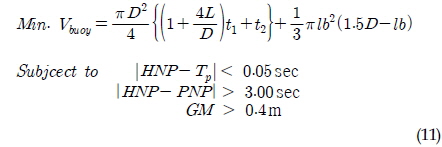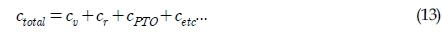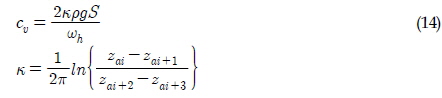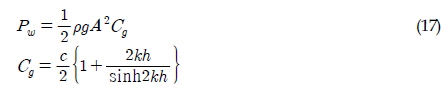근사기법을 활용한 공진형 파력발전 부이의 발전량 추정 및 최적설계

doi:10.5574/KSOE.2013.27.1.085

OA학술지
Journal of Ocean Engineering and Technology

근사기법을 활용한 공진형 파력발전 부이의 발전량 추정 및 최적설계 Power Estimation and Optimum Design of a Buoy for the Resonant Type Wave Energy Converter Using Approximation Scheme

DOI : 10.5574/KSOE.2013.27.1.085
Publish: Journal of Ocean Engineering and Technology Volume 27, Issue1, p85~92, 28 Feb 2013

ABSTRACT

This paper deals with the resonant type of a WEC (wave energy converter) and the determination method of its geometric parameters which were obtained to construct the robust and optimal structure, respectively. In detail, the optimization problem is formulated with the constraints composed of the response surfaces which stand for the resonance period(heave, pitch) and the meta center height of the buoy. Use of a signal-to-noise ratio calculated from normalized multi-objective results with the weight factor can help to select the robust design level. In order to get the sample data set, the motion responses of the power buoy were analyzed using the BEM (boundary element method)-based commercial code. Also, the optimization result is compared with a robust design for a feasibility study. Finally, the power efficiency of the WEC with the optimum design variables is estimated as the captured wave ratio resulting from absorbed power which mainly related to PTO (power take off) damping. It could be said that the resultant of the WEC design is the economical optimal design which satisfy the given constraints.

KEYWORD

공진 , 파력 발전 장치 , 전력 부이 , 경계요소법 , 반응 표면 , 전력 추출 시스템 , 에너지 취득율

본문

Collapse all

1. 서 론

파력 에너지를 이용한 발전시스템은 해수면의 상하 운동으로 인하여 발생하는 에너지를 기계적 운동을 통하여 전력을 생산하는 시스템이다. 파력을 이용한 에너지 추출 방법은 운동 에너지 변환 원리에 의해 크게 가동 물체형(Oscillating bodies), 진동 수주형(Oscillating water column), 그리고 월파형(Run up)으로 분류되며, 설치 형식에 따라 고정식(Fixed/Submerged)과 부유식(Floating)으로 구분된다. 우리나라의 경우 한국해양과학기술원에서 1993년부터 현재까지 부유식 및 착저식 진동 수주형, 월파형, 부유식 진자형 등 여러 형태의 파력발전 장치를 개발 완료 또는 진행 중에 있다(Kim et al., 2011). 그러나 Song et al.(2004)의 연구결과에 따르면 우리나라 해역의 파력 에너지는 평균 약 3kW/m로 타국 해역에 비하여 비교적 적은 편에 속한다. 이를 극복하기 위해서 Kweon et al.(2010)은 설치 해역의 최대 주기(Peak period)와 부이의 고유주기(Natural period)가 일치될 때 발생하는 공진을 이용한 파동에너지 추출시스템을 제안하였다. Kweon et al.(2010)이 제안한 공진형 파력발전 장치의 전력 부이는 극한 해양하중 및 불규칙 입사파의 다방향성을 고려하여 원기둥 형태의 단순 모델을 채택하였다. 그러나 해양파의 경우 파랑 스펙트럼의 협대역 특성으로 인하여 전력 부이의 공진을 위한 최적 설계가 요구된다(Koh et al., 2012).

해양 구조물의 최적화 설계는 1990년대 초반부터 다양한 목적을 위하여 여러 기법들이 적용되었다. Birk et al.(2004)은 반잠수식(Semi-submersible) 해양 구조물의 Column과 Pontoon 형상 변화에 따른 휴지시간(Downtime)과 수명(Lifetime)의 최적 설계로부터 SQP(Sequential quadratic programming), GA(Genetic algorithms), 그리고 SA(Simulated annealing) 최적화 기법을 비교․검토하였다. 또한 Colby et al.(2011)은 EA(Evolutionary algorithms)법을 이용하여 파력 발전 장치의 최대 발전량획득을 위한 밸러스트 형상 최적 설계를 실시하였다. 본 연구에서는 시스템의 응답을 전체 설계영역에서 적당한 정확도를 갖는 값으로 표현하는 근사 최적화 기법을 적용하였으며, 그 중 설계 영역의 여러 실험 점에서 실험된 결과를 기초로 시스템의 응답에 대한 전역적인 근사식을 구하는 반응 표면법(Roux et al., 1998)을 통하여 최적화를 실시하였다. 그러나 각 실험의 특성치 계산을 위해 소요되는 전산적, 시간적 비용이 과도하므로 최소의 실험 횟수로 모든 수준의 설계 변수를 고려하기에 적절한 직교 배열표(Phadke, 1989)를 통한 반응 표면법을 활용하였다. 반응 표면은 경계요소법을 적용한 ANSYS AQWA 상용프로그램을 통하여 4인자 3수준(L_g(3⁴))의 직교 배열표로부터 부이의 경심 및 수직/종 운동의 고유주기를 획득하여 구성하였으며(ANSYS, 2010), 부이의 공진 및 안전성에 대한 제약조건을 만족하는 최적의 설계변수를 도출하였다. 또한 최적 설계변수를 적용한 전력 부이의 생산 가능한 최대 발전량 및 발전 효율을 추정하였다.

2. 부이 운동 문제의 정식화

선형포텐셜 이론을 가정하여 전력 부이의 파랑중 운동특성을 살펴보았다. 파가 주파수 ω를 갖고 조화운동을 한다고 가정하면 속도포텐셜은 ϕ(x,y,z,t)=Re[ϕ(x,y,z)e^−iωt이다. 전체 속도포텐셜은 입사파, 회절파, 그리고 방사파 속도포텐셜의 합으로 식 (1)과 같이 쓸 수 있다.

여기서 x_j는 부유체의 운동변위이다. 입사파는 x축의 양의 방향으로 들어온다고 가정하였다. β의 입사각을 가지고 들어올때 입사파 포텐셜은 다음과 같이 쓸 수 있다.

여기서 A는 입사파의 진폭이며, 주파수 ω는 파수 k와 선형 분산식(ω²=gktanhkh)을 만족한다.

   2.1 경계요소법

회절파와 방사파의 속도포텐셜을 구하기 위한 수치해석 기법으로 유체 경계면을 대상으로 하는 경계요소법을 사용하였다. 경계요소법은 Green 정리에 따라 경계면에 특이점을 분포시켜 속도포텐셜과 법선방향 속도를 구하는 방법으로 특이점 분포법이라고도 불리어지며 다음과 같은 적분방정식으로 시작된다.

여기서 C()는 표면각이며, 는 평형상태에서 침수표면적, 그리고 G()는 특이함수(또는 Green 함수)이다. 위에 주어진 적분방정식을 행렬식으로 표현하기 위해 경계요소들로 이산화하는데 본 연구에서는 요소형상과 요소에서의 물리량들이 일정하다고 가정하는 일정경계요소법(Constant boundary element method)을 사용하였다.

   2.2 파기진력과 동유체력

경계요소법을 이용하여 물체표면에서의 속도포텐셜이 얻어지면 베르누이 방정식(P=−ρ(𝜕ϕ/𝜕t)으로부터 동압력을 구하고 이를 물체표면에 따라 적분하면 파기진력과 동유체력을 구할 수 있다. 파기진력은 입사파와 회절파의 속도포텐셜으로부터 아래와 같이 얻어진다.

여기서 ni는 상에서의 법선 벡터의 i방향 성분으로 물체의 바깥 방향을 양의 방향으로 잡았다.

식 (4)의 우변을 ϕ_I와 ϕ_d로 분리하여 전개할 경우, ϕ_I와 관련된 항을 Froude-Krylov힘이라 부르며 ϕ_d 관련항을 회절력(Diffraction force)이라 한다. 부유체의 운동에 기인한 방사력(Radiation force)은 방사포텐셜로부터 얻어지는데 아래 식과 같다.

위 식의 결과는 아래와 같이 실수부와 허수부로 나눌 수 있다.

여기서 부가질량 a_ji는 물체의 운동에 의해 야기된 유체운동의등가관성질량이며, 감쇠계수 b_ji는 방사파 발산에 따른 에너지 소산율이다.

앞에서 구한 파기진력, 동유체력, 정유체력을 사용하여 6자 유도 운동방정식을 구성하면 다음과 같다.

여기서 m_ji는 부유체의 질량 행렬, c_ji는 정유체력으로부터 얻어지는 복원력 계수를 나타낸다. 6자유도(surge, sway, heave, roll, pitch, yaw) 운동이 연성된 운동방정식을 풀어 각 운동 모드의 운동 변위를 구한다.

부이의 흘수와 입사파 주파수의 관계는 부이의 수직운동에 대한 공진주파수 계산 식(=C/(m+a))으로부터 구할 수 있으며, 원형 실린더일 경우 다음과 같이 계산할 수 있다.

여기서, d는 흘수, C는 복원력, ρ는 물의 밀도, A_ω 은 부이의 수선면적을 나타내며, ω_h와 a는 각각 부이의 수직운동에 대한 공진주파수와 부가질량이다. 본 연구에서 개발된 부이의 밑부분은 구형 캡으로 되어 있어 위의 간략식으로부터 대략적인 흘수를 구한 후 AQWA 프로그램으로부터 부유체의 질량 및 형상에 따른 평형상태에서의 정확한 흘수를 계산하여 보정하는 방식을 취하였다.

3. 근사 최적화 설계

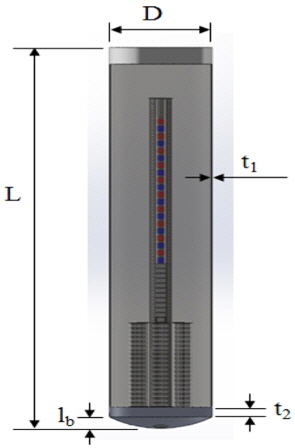
실험 계획법(Design of experiment)은 해결하고자 하는 문제에 대하여 실험 방법과 데이터 취득, 그리고 데이터 분석을 최소의 실험 횟수에서 최대의 정보를 얻을 수 있는가를 계획하는 것이다(Park, 2009). 실험 계획법을 통하여 각 인자의 결과에 대한 영향을 정량적으로 파악할 수 있으며 최적 값의 조건을 찾을 수 있다. 공진형 파력발전 전력 부이의 설계 변수는 Fig. 1과 같이 부이의 직경(D), 높이(L), 두께(t₁), 그리고 밑면 두께(t₂)로 선정하였다. Table 1은 각 설계변수에 대한 수준을 나타내며, L_g(3⁴)의 직교 배열표(Table 2)에 대입하여 최적설계를 위한 각 실험별 특성치 계산을 수행하였다.

[Fig. 1] Design variables of the power buoy

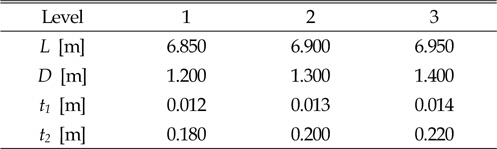
[Table 1] Level of design variables

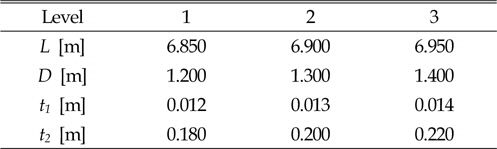
Level of design variables

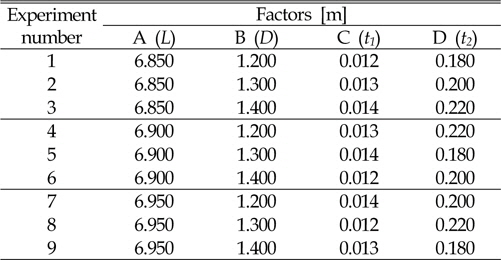
[Table 2] Experimental layout using an Lg(34) orthogonal array

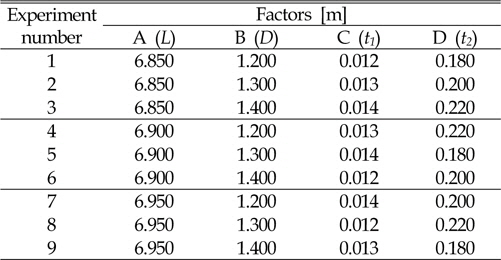
Experimental layout using an Lg(34) orthogonal array

   3.1 반응 표면법

반응 표면법은 여러 설계 변수의 복합 작용으로부터 반응변수에 영향을 주고 있을 때, 반응의 변화가 이루는 반응 표면에 대한 통계적인 분석법을 일컫는다. 최소 자승법을 이용한 이차 다항식 형태의 회귀 모델은 다음과 같이 정의된다.

여기서 a는 회귀 모델을 근사 계수이며, e는 랜덤 오차 벡터이다. 실험 계획법을 이용하여 산출되는 n개의 실험으로부터 실제 반응 벡터 g와 k개의 기저 변수로 표현되는 행렬 x가 주어지면 g와 x의 관계식을 구할 수 있다. 앞서 구한 각 실험들의 반응 값으로부터 수직 운동 및 종 운동의 고유 주기와 경심에 대한 회귀 모델을 식 (10)에 나타내었다.

여기서 밑첨자 HNP(Heave ntural period), PNP(Pitch natural period)는 각각 부이의 수직 운동 및 종 운동에 대한 고유 주기이며, 밑첨자 GM은 경심의 높이이다. x₁은 부이 높이(L), x₂는 부이 직경(D), x₃은 부이 두께(t₁), x₄는 바닥면 두께(t₂)를 각각 의미한다.

   3.2 부이 설계 변수 최적화

본 연구에서는 부이의 공진과 안전성에 대한 제약 조건 하에서 제작에 소요되는 비용이 최소화되도록 식 (11)과 같이 최적화에 대한 정식화를 구성하였다.

여기서 Tp는 설치 해역의 최대 주기이다. 목적 함수는 부이 제작을 위한 최소 비용을 소요된 박판의 부피로 환산하여 구성하였다. 제약 조건은 전력 부이의 공진을 위하여 부이의 수직 운동에 대한 고유 주기와 설치 해역의 최대 주기의 차가 0.05sec 보다 작아야하며, 부이의 안정성을 고려하여 0.4m 이상의 경심 길이를 갖도록 하였다. 또한 부이의 종 운동으로부터 전력생산을 위한 수직 운동 저하 현상을 방지하고자 수직 운동과 종 운동 고유 주기에 대해 3.0sec 이상의 간격을 확보하였다.

4. 최적화 해석 결과

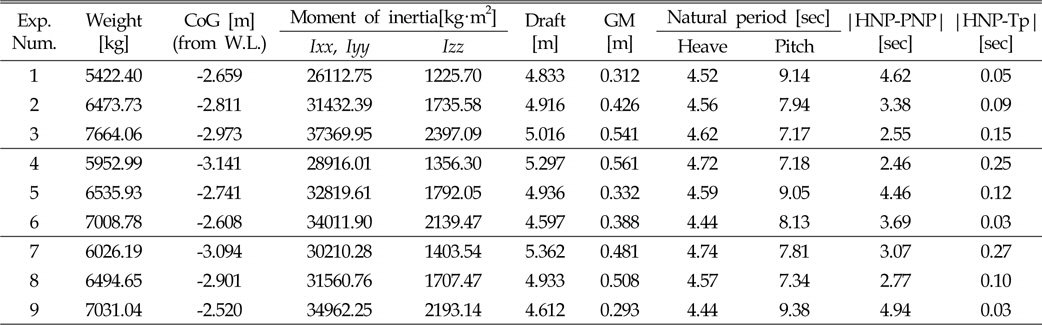
SolidWorks 상용 CAD 프로그램으로 모델링을 실시하여 각 설계 변수의 수준 수에 따른 부이의 중량과 무게 중심, 관성모멘트를 구하였으며(SolidWorks, 2001), 그에 따른 흘수와 수직 운동 및 종 운동에 대한 고유 주기 그리고 경심을 AQWA 프로그램을 이용하여 계산하였다(Table 3 참조). 1, 6, 9번째 실험만이 부이의 최적 설계를 위한 제약 조건을 만족하였다.

[Table 3] Analysis results according to orthogonal array Lg(34)

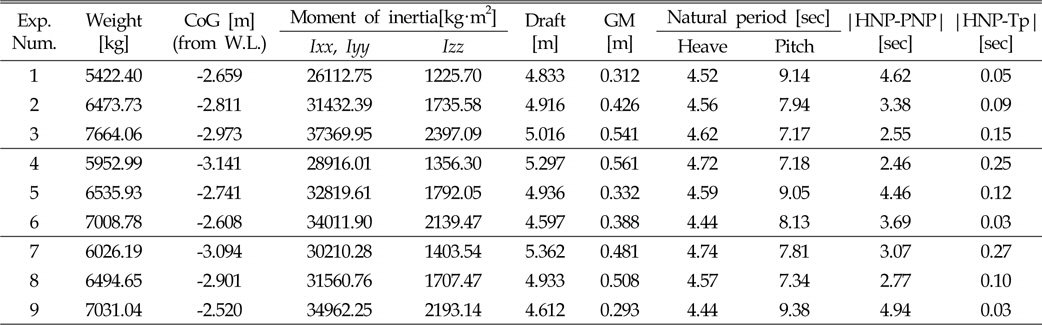
Analysis results according to orthogonal array Lg(34)

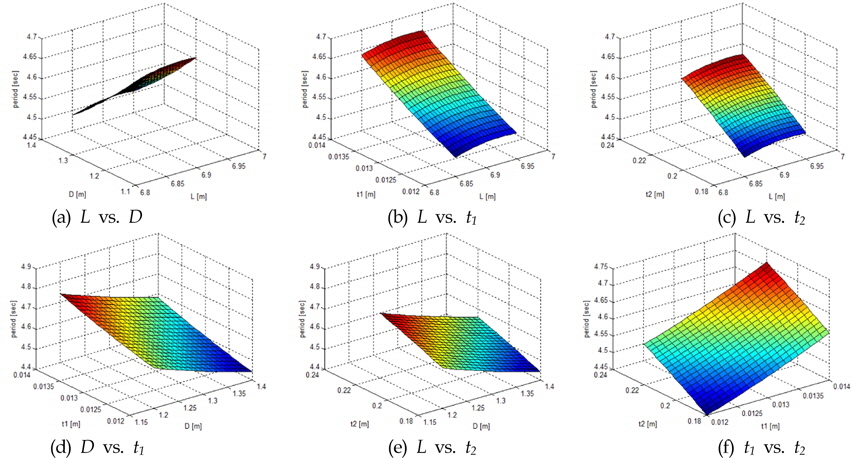
직교 배열표에 따른 9회의 실험으로부터 계산된 특성치를 이용하여 수직 운동 고유 주기에 대한 4가지 설계 변수 모든쌍의 반응 표면을 Fig. 2에 도시화 하였다. 각각의 그래프에서 나머지 2개의 변수 값은 중간 값으로 고정되었다.

[Fig. 2] Response surface results of the heave natural period as a function of the each design variable

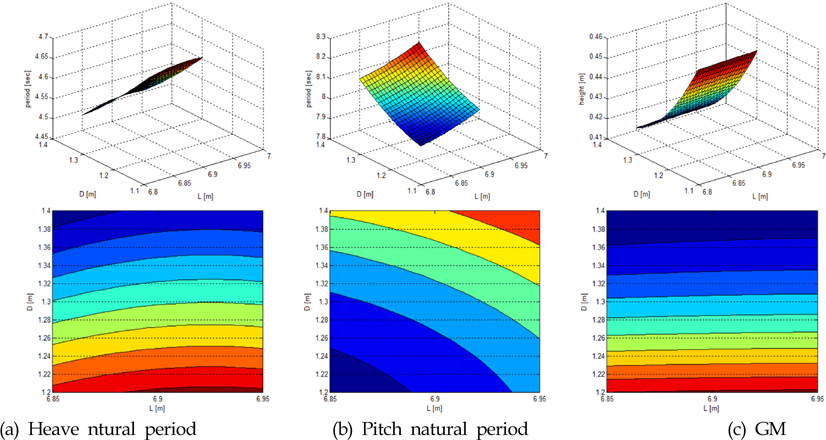
Fig. 3은 부이 설계에 가장 큰 영향을 미치는 부이의 높이(L)과 직경(D)에 대한 수직 운동 및 종 운동의 고유 주기, 그리고 경심 높이의 반응 표면과 등고선을 보여주고 있다. 부이의 직경이 작을수록 수직 운동의 고유 주기는 증가하며, 높이 변화는 고유주기에 거의 영향을 미치지 않았다. 부이의 안전성을 의미하는 경심의 높이 또한 직경 변화에 대해 민감하지만 높이 변화에는 둔감한 반응을 나타내었다. 그러나 종 운동의 경우 부이의 직경과 높이가 커질수록 고유 주기가 증가함을 확인하였다.

[Fig. 3] Response surface and contour diagrams of the: (a) HNP, (b) PNP, and (c) GM as a function of the D and L

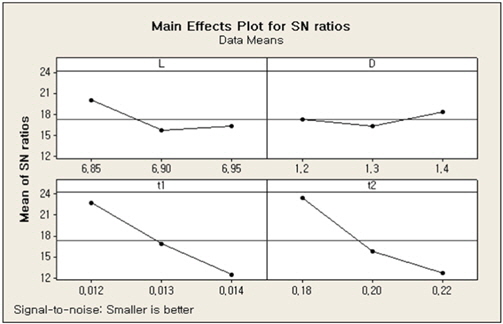
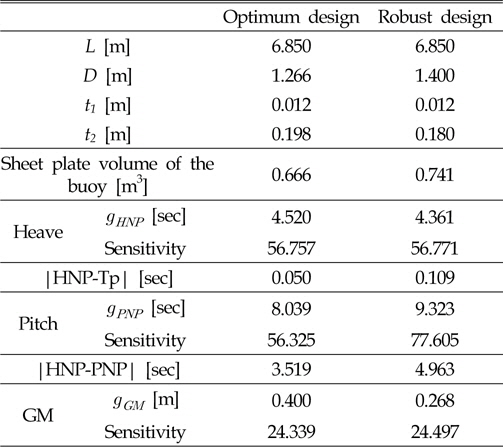
반응 표면으로 구성된 제약 조건을 만족하는 최적화 설계계산 결과를 타당성 검토를 위한 강건 설계(Robust design) 계산 결과와 함께 Table 4에 나타내었다. 강건 설계는 교란 인자의 영향을 최소로 유지하기 위해 모든 실험 결과로부터 각 설계변수에 대한 신호대잡음비(SNR, signal to noise ratio) 결과 값이 큰 수준을 채택하여 최적 조합을 구성하였다(Fig. 4 참조). SNR은 목적함수의 정의에 따라 망소(Lower is better, ƞ_s) 특성을 선택하였으며, 이는 관측치 y가 음의 값을 취하지 않고 작을수록 좋은 특성을 말하며 다음 식과 같이 계산된다.

[Fig. 4] S/N ratio value response for design variables

[Table 4] Comparison of the optimal and robust design results and sensitivity

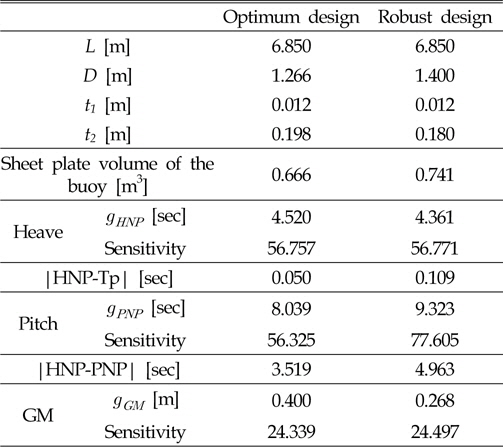
Comparison of the optimal and robust design results and sensitivity

최적 설계 결과 부이의 높이와 두께는 변수의 최소 수준(Level 1)을 보였으며, 부이의 직경과 밑면 두께는 중간 수준(Level 2)에 가까운 결과를 보였다. 또한 모든 제약 조건이 경계치 근처에서 결정되었다. 강건 설계의 경우, 부이의 직경을 제외한 모든 설계 변수가 최소 수준의 결과를 보여주었다. 목적 함수를 이루는 부이의 박판 부피는 최적 설계로 선정된 설계 변수로부터 계산된 결과 값이 강건 설계에 기인한 결과보다 더 작은 값을 나타내었으며, 최적 설계가 모든 제약 조건을 만족한 반면, 강건 설계의 경우 이산화된 설계 변수 수준만으로 최적 조합이 결정되므로 변수 수준의 특성으로 인하여 수직 운동 공진 주기와 안전성 확보를 위한 제약 조건 및 강건 설계에 대한 민감도 측면을 충분히 만족하지 못하였다.

5. 발전량 추정

공진형 파력발전 장치로부터 전력 생산 시 PTO(Power take off) 감쇠에 의해 전력 부이의 수직운동을 감소시키므로 입사파와 부이 설계가 정해지면 추출할 수 있는 에너지의 한계가 존재한다. 따라서 전력 부이의 운동에 영향을 미치는 모든 감쇠를 고려한 전력 부이의 고유 주파수 및 수직운동 RAO(Response amplitude operator) 재검토를 통하여 최대 발전량을 갖는 최적의 PTO 감쇠를 추정해야한다.

발전량 추정 해석을 위하여 다음의 가정을 도입하였다. 첫째로 총 감쇠는 식 (13)과 같이 점성 감쇠(Viscous damping), 방사 감쇠(Radiation damping), PTO 감쇠 및 기타 감쇠(재료 감쇠, 구조 감쇠 등)로 구성되나, 기타 감쇠의 경우 타 감쇠에 비해 그 값이 작으므로 무시한다. 즉, 점성 감쇠와 방사 감쇠를 제외한 모든 감쇠는 PTO 감쇠로 전환되며, 파력 발전 장치를 통한 전력 생산 시 PTO 감쇠는 최대이다.

여기서 c_v는 점성 감쇠, c_r은 방사 감쇠, c_PTO는 PTO 감쇠를 나타낸다. 점성 감쇠는 다음 식 (14)와 같이 무차원 감쇠 계수의 함수로 표현되며, 무차원 감쇠 계수는 자유감쇠운동 실험(Free decay test)으로부터 획득할 수 있다. 방사 감쇠는 경계요소법을 적용한 수치해석을 통하여 계산하였다.

여기서 k는 무차원 감쇠 계수, ρ는 물의 밀도, g는 중력 가속도, S는 전력 부이의 수선 면적, 그리고 ω_h는 전력 부이의 수직운동 고유 주파수를 나타낸다. 무차원 감쇠 계수는 자유감쇠운동 실험 결과(k=0.0233)로부터 획득하였다.

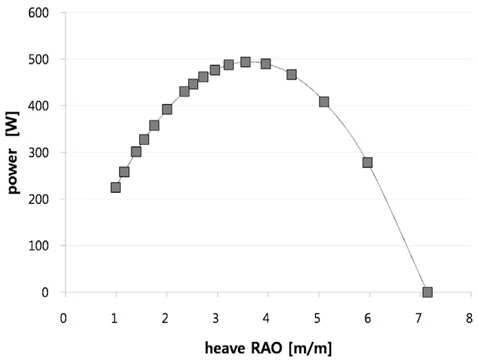
수직운동을 하는 파력발전 장치로부터 획득 가능한 단위 주기당 에너지는 식 (15)와 같이 계산되며, 이 때 수직운동 진폭과 관련된 수직운동 RAO가 PTO 감쇠와 반비례 관계에 있으므로 최대 에너지를 추출할 수 있는 최적의 수직운동 RAO와 PTO 감쇠를 획득해야 한다.

여기서 ω는 입사파 주파수, ξ는 전력 부이의 수직운동 진폭을 나타낸다.

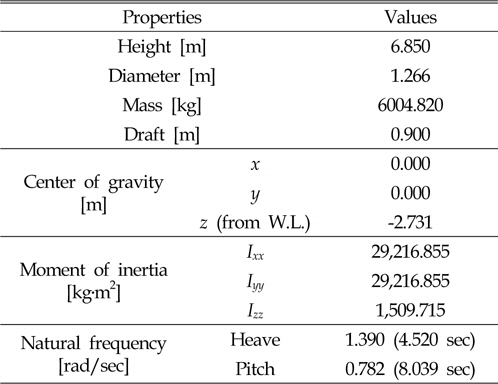
계산 모델은 최적 설계 결과를 적용하였으며, 상세 제원을 Table 5에 나타내었다. 점성 감쇠와 방사 감쇠를 기본 감쇠로하여 추가되는 PTO 감쇠 변화에 따른 부이의 수직운동 RAO를 각 PTO 감쇠별 감쇠 고유 주기(o)와 함께 Fig. 5에 나타내었다. 예상했던 바와 같이 PTO 감쇠가 증가할수록 공진 영역에서의 수직운동 RAO는 감소하였으나, 감쇠 고유 주기는 비감쇠 고유 주기와 매우 유사한 값을 보여 PTO 감쇠가 고유주기에 미치는 영향은 극히 미미한 것으로 확인하였다.

[Table 5] Specification of the power buoy model for the power estimation

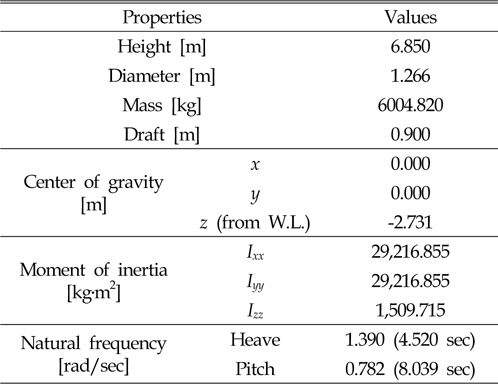
Specification of the power buoy model for the power estimation

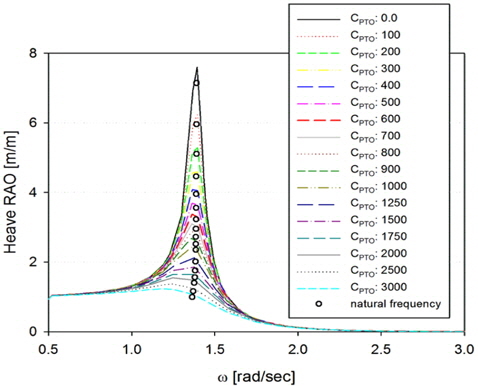
[Fig. 5] Heave RAOs and damped natural frequencies of the buoy with various PTO damping according to the incident wave frequency

공진 영역에 속하는 입사파 주파수(ω=1.402rad/sec)에 대해 PTO 감쇠 증가에 따른 부이의 수직운동 RAO 변화를 Fig. 6에 나타내었다. 앞서 언급한 바와 같이 PTO 감쇠가 증가할수록 수직 운동 RAO는 지수함수적으로 감소하였으며, PTO 감쇠가 3000kg/sec 일 때, 부이가 자유 표면을 따라 운동하는 RAO=1의 값을 보였다.

[Fig. 6] Heave RAOs of the buoy according to the PTO damping at resonance frequency(ωh=1.402rad/sec)

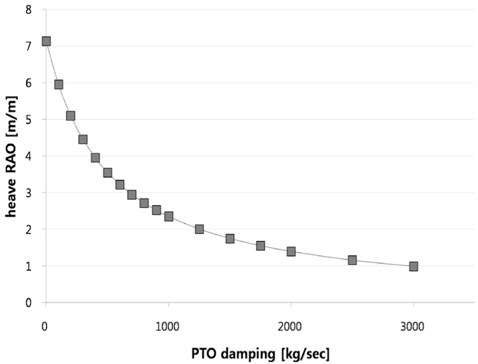
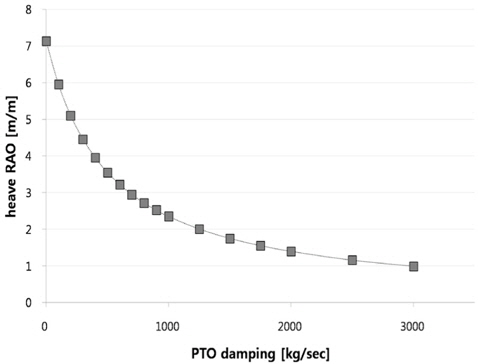
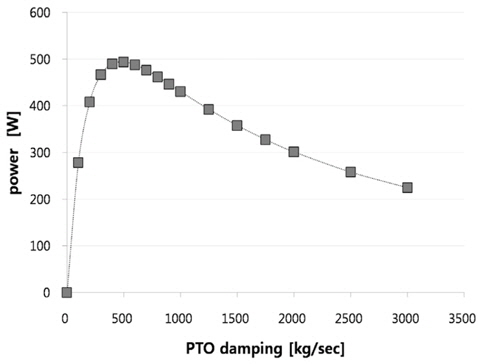
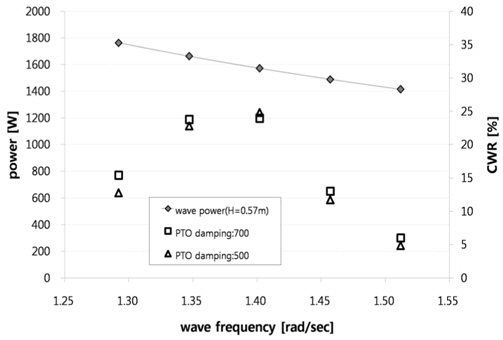
Fig. 7과 Fig. 8은 입사파 파고가 설치 예정 해역의 연평균 유의파고(Significant wave height)인 H_s=0.57m일 때, PTO 감쇠와 전력 부이의 수직 운동 변화에 따른 발전량 변화 추이를 보여주고 있다. PTO 감쇠가 약 500kg/sec 에서 최대 발전량(약493.93W)을 보였으며, 최대 발전량을 갖을 때, 수직운동 RAO는 약 3.55를 나타내었다.

[Fig. 7] Estimated power of the buoy according to the PTO damping at resonance frequency(ωh=1.402rad/sec)

[Fig. 8] Estimated power of the buoy according to the heave RAO at resonance frequency(ωh=1.402rad/sec)

공진형 파력발전 전력 부이의 발전 효율을 추정하기 위하여 식 (16)과 같이 에너지 취득율(CWR, capture width ratio) 계산을 실시하였다(Hagerman and Bedard, 2003).

여기서 P_ω는 다음 식과 같이 단위 폭당 단위 주기당 파랑 에너지이다.

여기서 C_g는 입사파의 군속도, c는 입사파의 위상속도이다. Fig. 9는 입사파 파고가 H=0.57m일 때, 입사파 주파수 변화에 따른 파랑 에너지 및 전력 부이의 에너지 취득율, 즉 발전 효율을 보여주고 있다. 입사파 주파수가 증가함에 따라 파랑 에너지가 감소하지만, 전력 부이의 공진 주파수에 해당하는 파가입사할 경우 PTO 감쇠 500kg/sec에서 약 25％의 최대 발전효율을 나타내었으며, 이 때 발전량은 약 493.93W이다.

[Fig. 9] Period-averaged wave power(◆) and the CWR(PTO damping 700(□), PTO damping 500(△)) of the buoy according to the incident wave frequency

5. 결 론

반응 표면으로 구성된 제약 조건을 만족하며 부이 제작비를 최소로 하는 공진형 파력발전 전력 부이의 최적 설계 및 발전량 추정으로부터 다음과 같은 결론을 얻을 수 있다.

(1) 직교 배열표에 입각한 최소 횟수 실험으로부터 부이의 중량과 무게 중심, 관성 모멘트에 따른 흘수와 경심 그리고 전력 부이의 고유 주기를 계산하여 제약 조건의 기반이 되는 반응 표면을 구성하였다.

(2) 파력발전 장치 설치 예정 해역에서 전력 부이의 공진을 유도하기 위한 부이의 수직 운동 고유 주기와 부이의 안전성및 전력 생산에 직접적 영향을 미치는 수직 운동 확보를 위한 제약 조건을 제시하였다.

(3) 부이 제작에 소요되는 박판 부피 계산식으로부터 부이 제작비를 최소화하는 목적 함수를 구성하여 제약 조건을 만족하는 부이의 형상 및 무게에 대한 설계 변수(직경, 높이, 원기둥 및 밑면 두께)를 선정하였다.

4) 파력 발전 장치를 통한 전력 생산 시 PTO 감쇠를 최대로 가정하여 총 감쇠계수를 고려한 부이의 수직 운동으로부터 공진형 파력발전 전력 부이의 최적 PTO 감쇠, 최대 발전량 및 발전효율을 추정하였다.

추후 각 실험별 추정 발전량으로부터 반응 표면을 구성하여 최소 제작비용과의 다목적 최적화를 통한 전력 부이 최적설계를실시할 예정이다.

참고문헌

1. 2010 ANSYS AQWA Reference Manual
2. Birk L., Clauss G.F., Lee J.Y 2004 Practical Application of Global Optimization to the Design of Offshore Structures [Proc. of 23rd Int. Conf. on Offshore Mechanics and Arctic Engineering (OMAE'04)] P.567-579
3. Colby M., Nasroullahi E., Tumer K. 2011 Optimizing Ballast Design of Wave Energy Converters Using Evolutionary Algorithms [GECCO'11] P.1739-1746
4. Hagerman G., Bedard R. 2003 Guidelines for Preliminary Estimation of Power Production by Offshore Wave Energy Conversion Devices
5. Kim Y.D., Hong K.Y., Shin S.H., Ryu H.J., Kim S.H., Park J.Y. 2011 A Technical Trend Analysis on Wave Energy Converting Technology [Journal of Ships & Ocean Engineering] Vol.51 P.73-80
6. Koh H.J., Kim J.R., Cho I.H., Ruy W.S. 2012 Optimum Design of a Buoy for the Resonant Type Wave Energy Converter Using Approximation Scheme [Proceedings of KSOE Fall Conference 2012] P.117-120
7. Kweon H.M., Kweon O.K., Kang J.H., Lee J.R., Park S.S., Cho I.H. 2010 Wave-Energy-Farm Utilizing by Resonance Power Buoy
8. Park S.H. 2009 Design of Experiments
9. Phadke M.S. 1989 Quality Engineering Using Robust Design
10. 2001 SolidWorks Mamual
11. Song M.Sl, Kim D.Y., Kim M., Hong K.Y., Jun K.C. 2004 Analysis of Wave Energy Density for Korean Coastal Sea Area Based on Long-Term Simulated Wave Data [Journal of the Korean Society for Marine Enviromental Engineering] Vol.7 P.152-157
12. Roux W.J., Stander N., Hatfka R.T. 1998 Response Surface Approximations for Structural Optimization [Int. J. Nume. Methods Eng.] Vol.42 P.517-534

이미지 / 테이블

[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 1 ] Design variables of the power buoy
[ Table 1 ] Level of design variables
[ Table 2 ] Experimental layout using an Lg(34) orthogonal array
[ ]
[ ]
[ ]
[ Table 3 ] Analysis results according to orthogonal array Lg(34)
[ Fig. 2 ] Response surface results of the heave natural period as a function of the each design variable
[ Fig. 3 ] Response surface and contour diagrams of the: (a) HNP, (b) PNP, and (c) GM as a function of the D and L
[ Fig. 4 ] S/N ratio value response for design variables
[ Table 4 ] Comparison of the optimal and robust design results and sensitivity
[ ]
[ ]
[ ]
[ ]
[ Table 5 ] Specification of the power buoy model for the power estimation
[ Fig. 5 ] Heave RAOs and damped natural frequencies of the buoy with various PTO damping according to the incident wave frequency
[ Fig. 6 ] Heave RAOs of the buoy according to the PTO damping at resonance frequency(ωh=1.402rad/sec)
[ Fig. 7 ] Estimated power of the buoy according to the PTO damping at resonance frequency(ωh=1.402rad/sec)
[ Fig. 8 ] Estimated power of the buoy according to the heave RAO at resonance frequency(ωh=1.402rad/sec)
[ ]
[ ]
[ Fig. 9 ] Period-averaged wave power(◆) and the CWR(PTO damping 700(□), PTO damping 500(△)) of the buoy according to the incident wave frequency