A numerical scheme based on a mode superposition method is presented for the dynamic response analysis of a top-tensioned riser (TTR) under sheared current loads. The natural frequencies and mode shapes of the TTR have been calculated analytically for a beam with a slowly varying tension and pinned-pinned boundary conditions at the top and bottom ends. The lift coefficients and corresponding amplitudes used to estimate the vortex-induced modal force and damping for each mode were predicted via iterative calculations based on the input and output power balancing concept. Here, the power-in regions were controlled by the normal distribution function, for which the center was coincident with the lock -in location by local vortex-shedding, and the range was defined by the constant standard deviation for the reduced velocity by the local current speed. Finally, dynamic responses such as root-mean-squared displacement and stress were calculated using the mode superposition technique. In order to verify the presented scheme, a numerical calculation was performed for a TTR under an arbitrary linearly sheared current and linearly varying tension. A comparison with the results of the existing software showed that the presented scheme could give reliable and feasible solutions. Case studies were performed to investigate the effects of various current loads and tensions.
상부장력 라이저(Top-tensioned riser)는 해양에서의 석유 및 가스 생산을 위한 해양플랜트(Offshore plant)에 있어서 원유의 이송을 위해 해저시스템과 장력 다리 플랫폼(Tension leg platform) 등의 부유식 플랜트를 연결하는 핵심 구성품 중 하나이다. 상부장력 라이저는 수명기간 중 구조적 안전성 확보를 위해 해류, 파랑등 해양환경에 의한 외부하중을 잘 견디도록 설계되어야 한다. 상부장력 라이저가 설치되는 해역에 해류가 발생하는 경우, 라이저 주위에는 유체박리에 의한 와류 방출(Vortex shedding) 현상에 의해 라이저 표면에 주기적인 하중이 발생하며, 이러한 현상을 와류유기 진동(Vortex-induced vibration)이라 한다. 이 때, 와류방출 주파수가 라이저의 고유주파수(Natural frequency)에 가까워질수록 큰 진폭의 라이저 동적응답(Dynamic response)이 나타나는 Lock-in 현상이 나타나며(Park et al., 1999), 상부장력 라이저에 주기적인 응력을 발생시켜 장기적으로는 피로손상의 원인이 된다. 따라서 전통적으로 와류유기 진동은 상부장력 라이저 설계에 있어서 그 피로수명을 예측하기 위한 주요 하중인자로 고려되어 왔다. 특히, 최근 해양자원 개발영역이 천해에서 심해로 이동하면서 상부장력 라이저의 길이는 증가하고 있으며, 그에 따른 와류유기 진동 현상도 보다 광범위하게 나타나고 있다. 이에 와류유기 진동을 고려한 상부장력 라이저의 정도 높은 동적응답 해석기법에 대한 연구 필요성이 더욱 증대되고 있다.
와류유기 진동을 고려한 상부장력 라이저의 동적응답(Dynamic response)에 대한 해석모델로는 전산유체역학 모델(Computational fluid dynamics model)과 경험 모델(Empirical model)이 있다. 전산유체역학 모델로는 라이저를 2차원 스트립들(2 dimensional strips)의 조합으로 간주하고 각각의 스트립에 작용하는 유체동력학적 힘과 감쇠를 구하는 방법이 주로 적용되고 있으며, 보다 실제에 가까운 현상을 시뮬레이션할 수 있는 장점이 있으나 과도한 연산부담으로 인해 실용적으로는 적용에 한계가 있다. 반면, 경험 모델은 대부분 모드중첩법(Mode superposition method)을 기반으로 하고 있으며, 각각의 모드에 작용하는 유체동력학적 힘과 감쇠를 실험을 통해 기 확보된 데이터베이스를 활용하여 산정하여 반영하는 방법이다. 전산유체역학 모델에 비해 연산부담이 매우 적고, 모형 또는 실물시험 등과의 보정을 통해 지속적인 정도 향상이 가능하므로 실무적 관점에서 매우 유용한 방법이라 할 수 있다. 최근 들어 경험 모델을 기반으로 한 다양한 해석기법들이 제안되었으며, 이는 VIVA(Triantafyllou, 2003), VICoMo (Moe et al., 2001), VIVANA(Larsen et al., 2005), SHEAR7 (Vandiver and Li, 2005) 등의 프로그램으로 구현되어 실무에 활용되고 있다.
한편, 경험 모델을 이용한 와류유기 진동응답에 있어서 파워입력 범위 산정은 양력계수, 감쇠계수 추정 등과 같은 입력 요소들 못지 않게 매우 중요한 요소이다. 파워 입력 범위를 과도하게 넓게 산정할 경우 동적 응답이 실제에 비해 과도하게 추정될 수 있고 반대로 그 범위를 너무 좁게 산정할 경우 과소하게 추정될 수 있다. VIVANA, SHEAR7 등의 프로그램에서는 각각의 모드별 파워 입력 범위를 산정한 후 모드가 중첩되어 가진되지 않도록 범위를 조정하여 해석을 수행한다(Larsen et al., 2005; Vandiver and Li, 2005). 이 때, 조정된 범위 내에서는 파워가 균일(Uniform)하게 입력되는 것으로 간주하여 해석을 수행하는데, 최근 실해역 시험결과와의 비교연구에서 실제 응답보다 과도하게 추정된다는 보고가 있었으며, 이에 대한 대안으로 모드별 기여도를 고려해 확률적으로 입력파워를 분배하는 소위 시간분배(Time sharing technique) 기법이 제안되고 현재 SHEAR7 4.6 버전에 반영된 바 있다(Vandiver et al., 2011).
본 연구에서는 전단류 하중(Sheared current load)을 받는 상부장력 라이저의 와류유기진동에 의한 동적 응답 해석을 위한 기초연구로써 기존 프로그램에서 채택하고 있는 해석기법을 참고하여 모드중첩법 기반의 수치해석기법을 정립한다. 제안된 수치해석기법은 고유진동해석, 각 모드에 작용하는 양력 및 감쇠 추정, 모드 중첩에 의한 동적 응답 해석 등의 절차를 따른다. 이때, 와류방출에 의한 파워 입력 범위 산정을 위해 정규분포함수(Normal distribution function)를 적용한다. 수치해석기법의 타당성을 검토하기 위해 가상의 상부장력 라이저 모델에 대한 수치해석을 수행하고 그 결과를 기존 수치해석 프로그램에 의한 결과와 비교하여 적절한 해석인자를 도출한다. 이를 이용해 전단류와 장력의 변화에 따른 동적 응답 해석을 추가적으로 수행하고 그 결과 고찰을 통해 실무 적용 가능성을 검토한다.
길이가 지름에 비해 매우 큰 경우(약 200배 이상), 상부장력 라이저는 유연한 케이블로 간주할 수 있으며, 와류 방출에 의해 외력이 작용하는 경우 전체 동적 응답에 대한 지배방정식은 식 (1)과 같다(Vandiver and Li, 2005).
여기서,
전체 시스템의 동적 응답을 식 (2)와 같이 고유 모드의 중첩으로 가정하고 식 (1)에 대입하여 정리하면, 식 (3)과 같은 모드좌표계에서의 운동방정식을 얻을 수 있다.
여기서,
해류의 와류 방출에 의해 양력이 외력으로 작용하는 경우, 외력은 식 (8)으로부터 계산된다. 또한, 국부에 작용하는 힘과
여기서,
이와 마찬가지 방법으로
여기서, 𝛷′(
각각의 모드에 대해 입력 파워와 출력 파워의 평형(Input- output power balancing, )을 고려하면 식 (12)를 얻을 수 있다.
식 (12)에서 좌변과 우변의 분모 항은
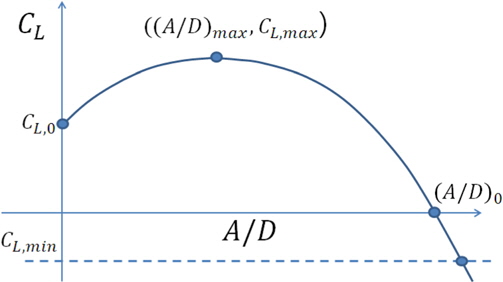
양력계수는 무차원 응답진폭(
유체동력학적 감쇠계수는 경험 모델을 적용하되 감소속도(Reduced velocity,
여기서,
식 (3)에서 감쇠항을 무시하고 조화가진을 가정한 고유치 문제의 해를 구하면 고유주파수와 고유모드를 구할 수 있으며, 식 (12)의 반복계산에 따라 구한 양력계수와 감쇠계수를 활용하면 모드중첩법에 의한 동적 응답을 산정할 수 있다.
상부장력 라이저에 대한 RMS 변위(Root-mean-squared displacement, (
여기서,
여기서,
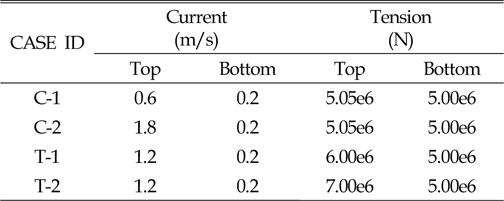
정립된 수치해석기법의 타당성을 검토하기 위해 가상의 상부장력 라이저 모델에 대한 수치해석을 수행하고 그 결과를 기존 프로그램인 SHEAR7(Vandiver et al., 2011)에 의한 결과와 비교하였다. Table 1은 수치해석 모델을 요약한 것이다. 해석모델은 양단이 단순지지(Pinned-pinned)되어 있고 강(Steel)으로 되어 있는 라이저이며, 그 길이는 1,000m, 지름과 강력 지름은 공히 0.6m로 설정하였다. 해류는 하단(Bottom) 0.2
[Table 1] Virtual top-tensioned riser model

Virtual top-tensioned riser model
[Table 2] Lift coefficient and damping model for numerical calculation
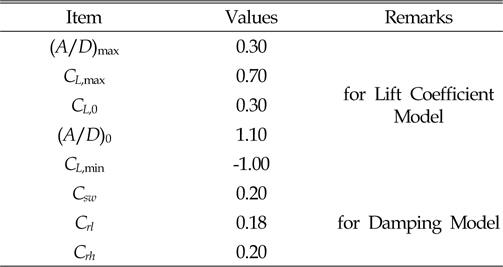
Lift coefficient and damping model for numerical calculation
한편 해석모델에 대한
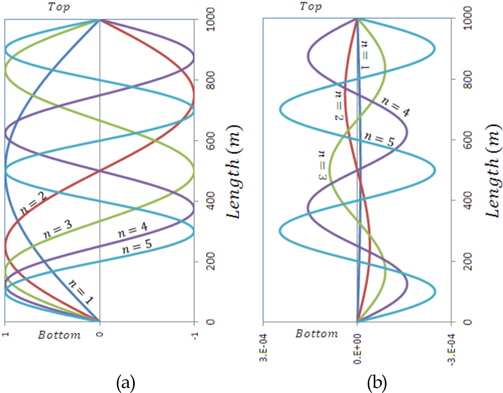
Table 3은 10차까지의 고유주파수 산정결과를 SHEAR7의 결과와 함께 정리한 것으로써, SHEAR7의 결과가 다소 높게 나타나며 고차모드로 갈수록 차이가 커지나 전반적으로 2.3% 차이 이내의 타당한 결과를 주고 있다. 이러한 차이는 본 연구에서는 라이저를 굽힘 강성이 없는 유연한 케이블로 간주한 반면, SHEAR7에서의 결과는 굽힘강성을 갖는 보(Beam)로 가정하였기 때문인 것으로 판단되며, 고유진동해석 시 정도 높은 해석기법을 활용할 경우 충분히 개선될 수 있을 것으로 사료된다. Fig. 2는 차수별 고유모드 형상과 곡률을 도시한 것이다.
[Table 3] Natural frequency calculation results
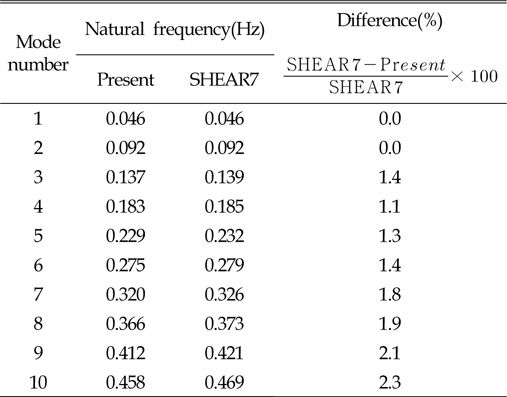
Natural frequency calculation results
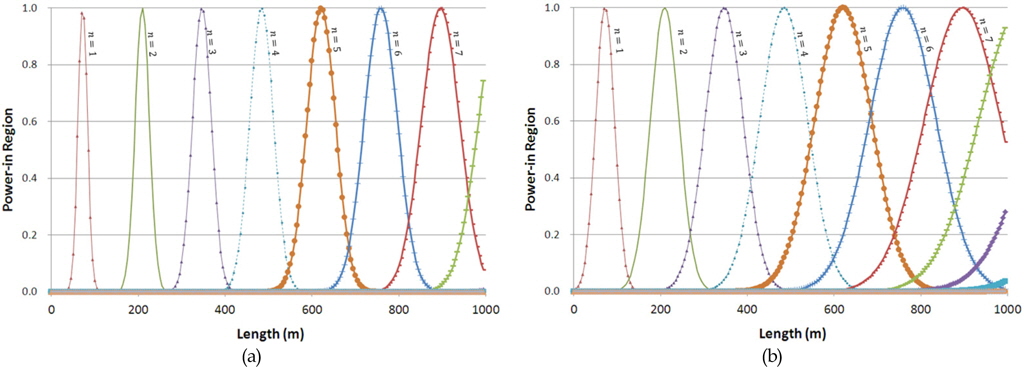
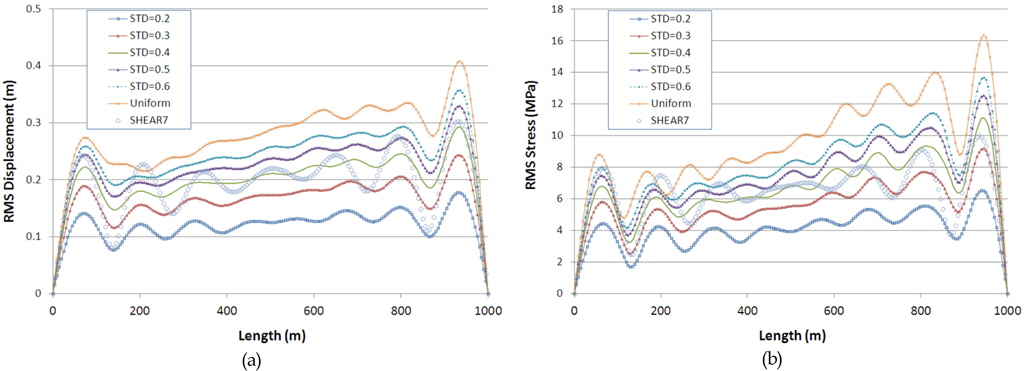
라이저의 모드별 가진범위(Power-in region)에 따른 해석결과의 변화를 살펴보기 위해 STD가 0.2, 0.3, 0.4, 0.5, 0.6인 정규분포 함수로 가진범위를 정의한 경우에 대한 수치해석을 수행하였다. Fig. 3은 STD가 0.2와 0.4인 경우의 가진범위를 대표적으로 도시한 것이며, STD가 커질수록 가진범위가 넓어짐을 확인할 수 있다. Fig. 4는 RMS 변위와 RMS 응력을 STD 별로 도시한 것이며, 본 연구에서 정립한 해석기법의 타당성과 적절한 STD값을 도출을 위해 SHEAR7에 의한 해석결과와 함께 나타내었다. 이로 부터 STD가 클수록 동적 응답이 과도하게 산정되고 있으며, 특히 일부 프로그램에서 적용하고 있는 균일 분포 함수(Uniform distribution function)를 가정하는 경우 상당한 오차가 발생함을 알 수 있다. 전반적으로 하단(Bottom)부근에서는 STD가 0.6인 경우, 상부(Top)부근에서는 STD가 0.4인 경우, SHEAR7의 결과와의 부합성이 높게 나타나며, 평균적으로는 STD가 0.4인 경우의 부합성이 크게 나타나고 있다. 이는 본 연구에서 제안한 정규분포함수를 이용해 파워입력 범위를 정의하되 적절한 STD을 선정할 경우 신뢰성 높은 해석이 가능함을 의미한다. 참고로, 본 해석에서는 전단류에 의해 가진 가능성이 있는 주파수를 고려할 때 최고차 모드는 8번으로 파악되었으나 실제 계산에 있어서는 고차 모드영향을 고려해 1.5배에 해당하는 13번까지의 모드를 포함하여 해석을 수행하였다.
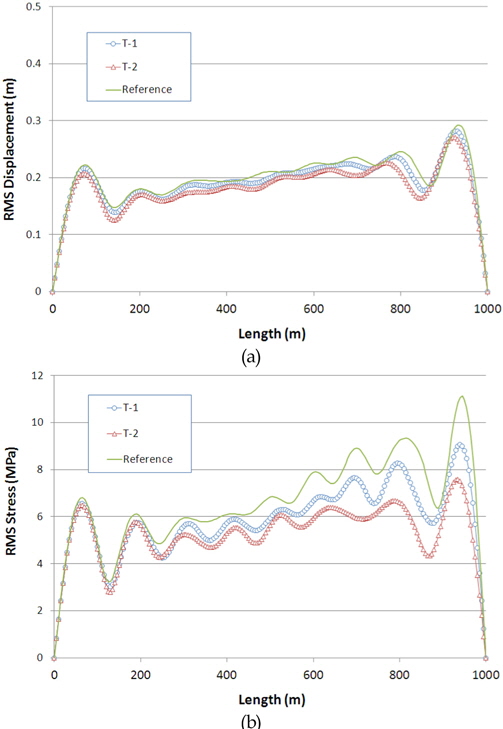
한편, 본 연구에서 정립한 해석기법을 이용해 유효장력(T-1, T-2), 전단류(C-1, C-2) 변화에 따른 CASE 별 수치해석을 수행하고 그 결과를 살펴보았다. 이 때, 입력파워 범위 정의를 위한 정규분포함수의 STD는 0.4를 적용하였다. Table 4는 CASE별 해석에 적용된 유효 장력과 전단류를 정리한 것이다.
[Table 4] Tension and current variation for case study
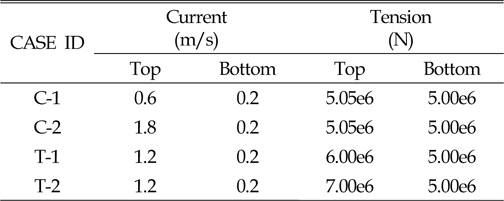
Tension and current variation for case study
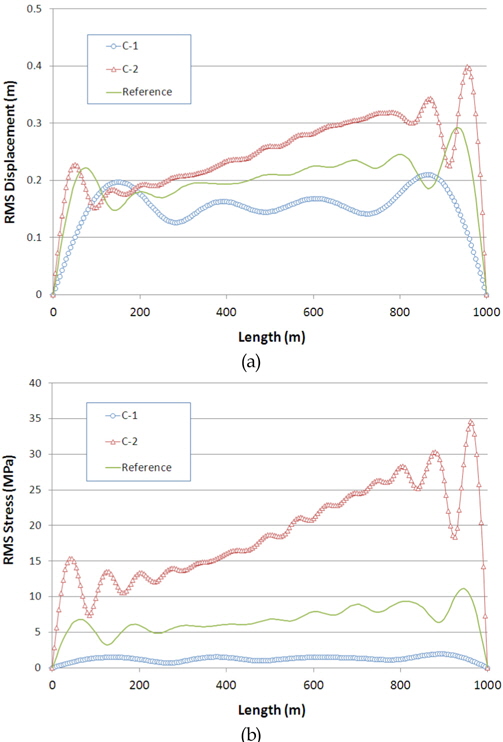
Fig. 5는 전단류 변화(C-1, C-2)에 따른 라이저 동적응답해석 결과를 Fig. 4의 STD=0.4(Reference)에 대한 것과 비교하여 나타낸 것이다. 변위(Fig. 5(a))의 경우, 전단류가 강해질수록 커지고 약할수록 작아지는 특성이 나타나며, 최대값의 위치도 함께 변화하고 있다. 응력(Fig. 5(b))의 경우, 유사한 양상을 보이지만 응력의 변화폭이 매우 크게 나타나고 있다. 전단류가 강해질수록 고차모드에 의한 기여도가 강하게 나타나고 있음을 확인할 수 있으며, 이는 변위 변동폭이 유사한 수준이더라도 고차모드가 지배적인 경우 응력의 변동폭이 크게 나타날 수 있으므로 응력관점에서 저차모드 보다는 고차모드에 대한 제어가 우선되어야 함을 의미한다.
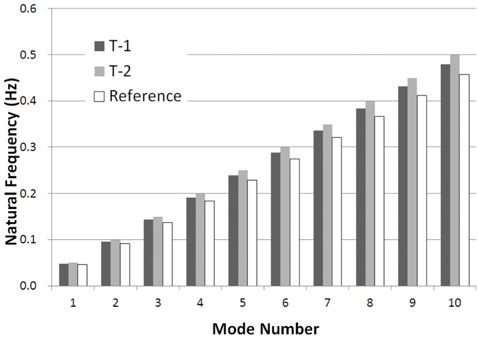
Fig. 6은 유효장력 변화(T-1, T-2)에 따른 라이저 고유주파수를 기존결과(Fig. 4의 STD=0.4(Reference))와 함께 막대그래프로 나타낸 것이다. 기존 결과에 비해 큰 고유주파수를 보이며, 이는 유효 장력의 증가에 따른 영향을 판단된다. Fig. 7은 유효장력 변화에 따른 동적응답해석결과를 Fig. 4의 STD=0.4(Reference)에 대한 것과 비교하여 나타낸 것이다. 기존 결과에 비해 유효장력이 증가함에 따라 변위와 응력이 감소하고 있음을 알 수 있다. 이는 유효장력의 증가가 고유주파수를 증가시키므로 동일한 전단류 하중 하에서 동적응답에 기여하는 고유모드의 수가 감소했기 때문인 것으로 판단된다. 또한, 유효장력 증가에 따라 변위보다는 응력의 변화폭이 크게 나타나고 있다. 이는 유효장력이 증가하면서 응력에 크게 기여하는 고차모드의 영향이 사라지기 때문인 것으로 판단된다.
본 연구에서는 전단류 하중(Sheared current load)을 받는 상부장력 라이저의 와류유기진동에 의한 동적 응답 해석을 위한 기초연구로써 기존의 프로그램에서 해석기법으로 채택하고 있는 모드중첩법 기반의 수치해석기법을 정립하였다. 이 때, 와류 방출에 의한 파워 입력 범위 산정을 위해 정규분포함수를 도입하고 가상의 상부장력 라이저에 대한 수치해석 결과와 기존 프로그램에 의한 결과를 비교하여 그 타당성을 검토하였다. 또한, 정립된 해석기법을 활용해 전단류와 유효 장력의 변화에 따른 CASE 연구를 수행하고 이들이 라이저의 동적 거동 특성에 미치는 영향을 검토하였으며, 다음과 같은 현상을 관찰할 수 있었다.
(1) 전단류가 강해질수록 라이저의 동적응답은 커지며, 특히 고차모드의 영향으로 변위보다는 응력의 변화폭이 크게 나타났다. 이는 변위 변화폭이 크지 않더라도 저차모드보다는 고차모드가 응력에 크게 기여함을 의미한다.
(2) 유효 장력이 증가하면, 라이저 고유주파수는 증가하고 응력은 감소한다. 이는 라이저의 강성이 증가하면서 고차모드의 영향이 감소하기 때문인 것으로 판단된다.
이상의 결과로부터 제안된 해석기법이 실무에 효과적으로 활용될 수 있을 것으로 기대되며, 향후, 보다 높은 정도 확보를 위해 모형 또는 실 규모 실험자료와의 비교를 통한 타당성 연구가 추가적으로 필요할 것으로 사료된다.