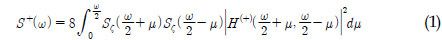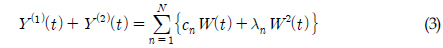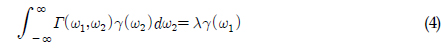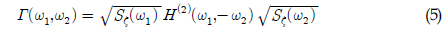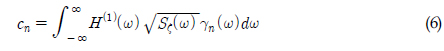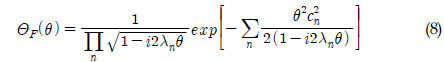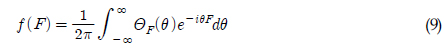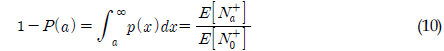This paper considered the prediction of the tension force in the design of a TLP tendon, particularly focusing on the springing problem. Springing is an important parameter that exerts a large tension in special cases. It is a nonlinear phenomenon and requires the 2nd-order wave loads to solve. In this paper, a new prediction method for springing and the resultant extreme tension on the tendon of a TLP is introduced. Using the 2nd-order response function computed using the commercial program WADAM, the probability density function of the 2nd-order tension is obtained from an eigenvalue analysis using a quadratic transfer function and sea spectra. A new method is then suggested to predict the extreme tension loads with respect to the number of occurrences. It is shown that the PDF suggested in this study properly predicts the extreme tension in comparison with the time histories of the 2nd-order tension. The expected tension force is larger than that from a linear analysis in the same time windows. This supports the use of the present method to predict the tension due to springing.
스프링잉(Springing)은 파의 합주파수(Sum-frequency) 성분이 TLP(Tension leg platform)의 고유주기와 가까운 경우에 발생하는 대표적인 비선형 공진 운동이다. 발생하는 고주파 진동은 텐돈(Tendon)의 설계하중 및 피로파괴에 영향을 미칠 수 있다. 따라서 TLP의 텐돈을 설계하기 위해서는, 설치 해역의 환경이 야기할 수 있는 스프링잉의 위험성을 파악하고 이를 설계에 반영 할 수 있는 적합한 예측 기술이 요구된다.
스프링잉 해석을 위해서는 부유체와 파에 대한 2차의 경계조건 문제를 해석하여야 한다. 2차의 저주파와 고주파 기진은 해양구조물의 운동 해석 측면에서 오랫동안 연구된 분야이다. 선박해양유체역학 분야에서 가장 널리 쓰이는 패널법은 TLP의 비선형 운동 해석에도 적용되어 왔다. 대표적으로 De Boom et al.(1983), Matsui et al.(1992), Matsui et al.(1993)은 주파수 영역에서 TLP의 비선형 합주파수 거동을 해석하였다. 또한, TLP의 거동 및 텐돈 장력의 비선형성을 관찰하기 위하여 시간 영역에서 이를 해석한 사례도 있다(Kim et al., 1995; Zou et al., 2004).
텐돈의 설계를 위해서는 해양 환경에 따른 장력의 거동을 통계적으로 파악할 필요가 있다. TLP의 스프링잉 거동은 정규분포를 따르지 않기 때문에, 시계열의 확률밀도함수를 찾기 위한 연구가 진행되었다. Kim and Yue(1991), Naess and Ness(1992), Naess(1994), Eatock Taylor and Kernot(1999)은 Kac and Siegert(1947)가 제안한 통계적 모델을 적용하여 비선형 스프링잉에 적합한 확률밀도함수를 제안하였다. 이를 통해 스프링잉은 정규 분포에 비하여 극한의 장력이 더 높은 빈도로 나타나는 것을 보여주었다.
현재까지의 스프링잉에 대한 연구들은 주로 거동을 계산하고, 통계적 특성을 파악하는 것이 일차적이 관심 사항이었다. 반면에 텐돈에 발생할 수 있는 최대의 장력에 대한 연구는 많지 않았는데, 이는 일반적으로 선형 운동에 의한 장력의 크기가 스프링잉이 야기하는 비선형 장력보다 훨씬 크기 때문이라고 볼 수 있다. 하지만, TLP 설계 기술을 향상시키기 위해서는 스프링잉이 야기할 수 있는 장력의 영향을 무시하는 것이 올바른 방향은 아니다. 어떠한 해상상태에서는 스프링잉으로 인한 장력이 커질 가능성이 높기 떄문에, 스프링잉으로 증가하는 장력의 최댓값을 파악하고 이를 설계에 반영함으로서 TLP 설계의 안정성뿐만 아니라 요소 기술의 정밀도를 높일 필요가 있다.
스프링잉이 포함된 비선형 해석 사례의 경우, 태풍과 같이 극한의 환경이 발생할 수 있는 상황에서 텐돈의 비선형 거동을 시간 영역에서 해석하는 연구가 일반적이었다(Kim et al., 1995; Zou et al., 2004). 그런데 시간 영역의 비선형 해석은 정밀한 해석이 가능한 장점은 있지만 계산 시간이 많이 소요되기 때문에, 해석을 수행할 수 있는 환경의 조합에 있어서는 다소 제한적일 수 있다. 따라서 대단히 많은 해석시간이 필요한 시간영역 해석을 진행하기에 앞서 스프링잉의 발생이 예상되는 해상 상태를 짧은 시간에 예측하고 이로 인한 장력의 크기를 추정하는 방법을 개발하는 것은 TLP의 텐돈 설계에 있어 해석의 효율성을 크게 높일 수 있다.
본 연구에서는 TLP의 설계에 이용될 수 있는 기법 개발을 목적으로, 스프링잉이 야기하는 장력의 최대 크기를 신속히 예측할 수 있는 기법을 연구하였다. 주파수 영역의 해석은 빠른 계산이 가능하며 실제 업무에서도 널리 쓰인다는 장점이 있기 때문에, 상용 프로그램을 이용하여 주파수 영역에서 비선형 합주파수 거동을 계산하였다. 2차 유체력 계산에는 상용 프로그램을 이용하였고, 이로 부터 얻은 운동의 2차 전달함수를 이용하여 장력의 전달함수를 구하였다. 장력의 전달함수로부터 확률밀도함수를 계산하였으며, 시계열을 생성하여 결과가 타당한 것을 확인하였다. 확률밀도함수를 이용하여 장력의 최댓값을 예측할 수 있는 방안을 제시하였으며, 직접 시계열을 생성한 결과와 비교하여 본 방법의 타당성을 확인하였다.
스프링잉은 2차 합주파수 기진력에 의해서 발생하는 운동이기 때문에, 2차 파랑 경계조건 방정식을 풀어야 한다. 2차 파랑 하중 및 운동에 대한 연구는 해양구조물 운동에서 대표적인 관심 분야이었으며, 현재 해석이 가능한 상용 프로그램이 널리 쓰이고 있다. 따라서 본 연구에서는 상용 프로그램인 WADAM을 이용하여 TLP의 2차 전달함수(QTF, Quadratic transfer function)를 계산하였다.
2차 전달함수로부터 합주파수 응답의 스펙트럼을 식 (1)과 같이 구할 수 있다(Kim and Yue, 1991). 여기서 𝑺ζ(𝜔) 는 주파수(𝜔)에 대한 파의 스펙트럼을 의미하며,
식 (1)에서 사용하는
선박 및 해양 구조물의 선형 거동에 대해서는 통계적인 예측기법이 많이 알려져 있다. 파고가 아주 크지 않은 경우, 불규칙해상 파는 정규 분포를 따르는 것으로 알려져 있다. 그리고 통상적인 파의 스펙트럼은 좁은 주파수 영역에 에너지가 집중되어 있으며, 이로 인해 야기되는 운동 또한 협대역(Narrow band)으로 볼 수 있다. 협대역 거동의 경우 운동의 크기는 Rayleigh 분포를 따르며, 이를 이용하여 단기 예측이 가능하다. 그러나 스프링잉은 합주파수 성분이 야기하는 비선형 운동이며, 발생하는 운동의 시계열은 정규 분포를 따르지 않는다(Naess and Ness, 1992). 따라서 시계열 분포를 나타낼 수 있는 적합한 확률밀도함수를 우선적으로 찾을 필요가 있다.
2차 응답의 확률밀도함수를 계산하는 방법으로 전달함수의 고유치(Eigenvalue)를 이용할 수 있다(Kac and Siegert, 1947; Neal, 1974; Kim and Yue, 1991). 전달함수를 이용하는 방법은 본 연구에서 주파수 영역의 해를 직접 이용하고자 하는 목적과 일치한다. 따라서 고유치 해석을 통하여 확률밀도함수를 계산하는 방법을 이용하였으며, 아래의 식 (3)~(9)를 통하여 그 과정을 간략히 나타내었다.
1차와 2차 응답의 시계열은 식 (3)과 같이 나타낼 수 있다.
에르미트 커널(Hermitian kernel)인
식 (4)는 이산화된 행렬식으로부터 구할 수 있으며, 이 때 이산화한 수만큼의 고유치를 구할 수 있다. 여기서 다루어지는 행렬은 에르미트 행렬이기 때문에 고유치는 모두 실수이다. 고유치와 고유함수가 구해지면 식 (6)과 (7)로부터 응답의 분산을 구할 수 있으며, 특성방정식은 식 (8)로부터 구할 수 있다. 식 (6)의
확률밀도함수를 구하는 식은 1차와 2차의 거동을 모두 포함하고 있다. 본 연구에서는 2차 스프링잉 하중에 의한 장력의 거동이 대상이기 때문에 1차 응답은 고려하지 않았다. 따라서 식 (7)과 (8)에서 1차 응답과 관련한 계수
확률밀도함수는 스프링잉이 나타나는 시계열의 분포를 예측할 수 있게 한다. 그러나 설계를 위해서는 시계열이 아니라 Zero-crossing peak의 확률론적 분포를 파악할 필요가 있다. 이를 이용하여 TLP의 설계 기준이 되는 장력의 최댓값을 파악할 수 있기 때문이다. 선형 프로세스에 적합한 Rayleigh 분포는 시계열이 정규분포라는 것을 가정하기 때문에 스프링잉에는 이용될 수 없다. 스프링잉에 적합한 예측 모델을 찾기 위하여, 파의 통계적 거동에서 최댓값을 예측하는 방법을 적용하고자 하였다. 임의의 불규칙 파에서 Peak의 확률밀도함수를 구하는 과정은 프로세스가 협대역(Narrow band)이라고 가정하여서 식 (10)과 같이 나타낼 수 있다(Ochi, 1998; Kim, 2008).
식 (10)에서
스프링잉은 TLP의 연직방향 운동이 합주파수에서 공진하는 경우에 크게 나타나는 비선형 현상이므로, 스프링잉의 응답은 협대역으로 가정할 수 있다. 이러한 유사성을 이용하면, 식 (10)을 스프링잉에 적용하여 최댓값을 예측해볼 수 있다. 그리고 스프링잉의 시계열은 평균이 0인 Stationary 프로세스라고 가정할 수 있으므로, 이 경우 해당 변수의 변위와 기울기는 서로 독립적이다(Kim, 2008). 따라서 스프링잉의 변위와 기울기에 대한 조건부확률은 식 (12)와 같이 각 확률밀도함수의 곱으로 나타낼수 있다.
식 (12)에서 응답과 기울기에 대한 분포는 식 (9)에서 구한 스프링잉의 확률밀도함수를 대입하여 사용할 수 있다. 이로부터 식 (10)을 이용하여 응답의 크기에 대한 확률밀도함수 및 누적밀도함수를 구할 수 있다. 식 (10)은 정규 분포에서 유도되는 Rayleigh 함수처럼 간략한 식으로 표현되지는 않는다. 적분에 필요한 확률밀도함수가 적분방정식과 푸리에 변환으로부터 계산되기 때문이다. 그러나 수치적인 접근으로 스프링잉의 Peak이 나타나는 확률의 분포를 계산할 수 있게 해준다. 따라서 원하는 기간 내에 발현하는 극한의 장력을 계산하는 목적으로 쓰일 수 있다. 실제 시계열을 분석하는 것보다, 상대적으로 빠른 계산으로 극한값의 분포를 예측할 수 있는 것이 장점이라 볼 수 있다.
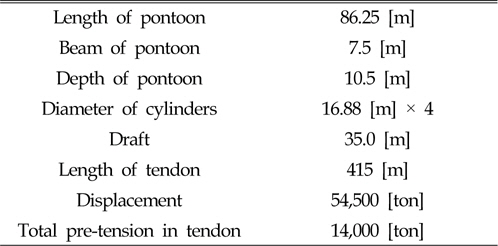
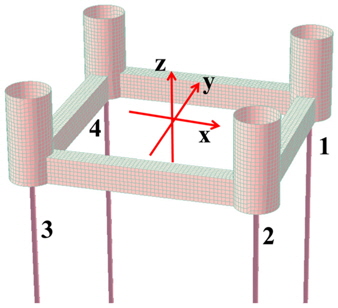
해석 모델인 TLP의 형상 및 주요 제원은 Table 1과 Fig. 1에 나타내었다. 4개의 텐돈이 각 원기둥 하단에 부착되어 있으며, 편의상 Fig. 1에서와 같이 1~4의 순서로 나타내었다. 좌표축의 수평 방향 원점은 TLP의 중심에 위치하며, 연직방향은 평균수면에 해당한다. 길이방향의 x축과 파의 진행 방향이 이루는 각을 선수각(Heading angle)으로 정의하였다.
[Table 1] Principal particulars of TLP
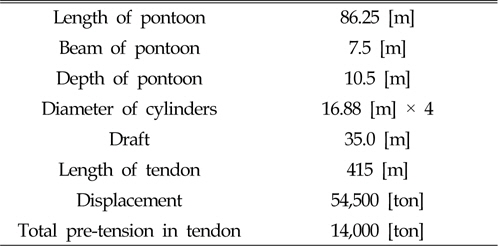
Principal particulars of TLP
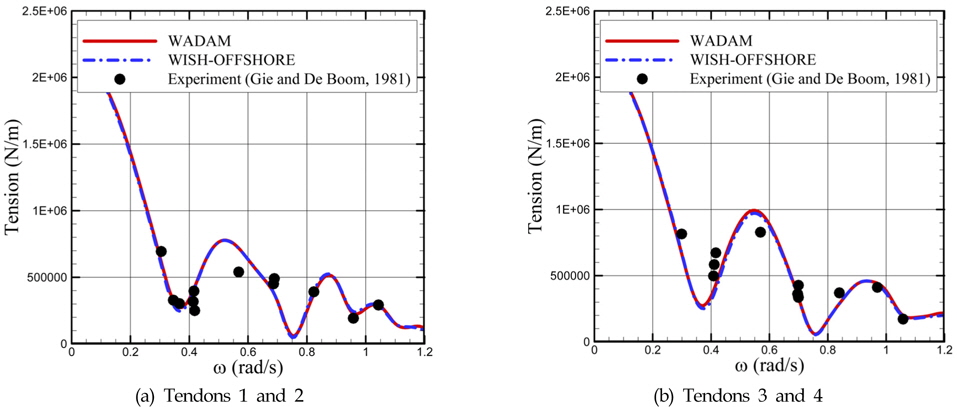
본 계산에서는 장력의 선형 응답을 해석하였고, 이를 다른 계산 및 실험과 비교하였다. 텐돈이 가해주는 복원력을 고려하여 TLP 운동의 전달함수를 구할 수 있으며, 이를 이용하여 텐돈이 TLP에 장착되는 지점의 거동을 계산할 수 있다. 장력의 크기는 선형 스프링으로 가정하여 텐돈이 늘어난 길이에 비례하는 힘으로 계산하였다. 비교를 위해 사용한 WISH-OFFSHORE 프로그램은 시간 영역에서 해양 구조물의 운동 해석을 위해 개발된 프로그램으로, TLP 및 Semi-submersible 등의 운동에서 적합한 해석 결과를 보여준 바 있다(Kim et al., 2012). Fig. 2에서와 같이 WADAM에서 구한 운동응답을 이용하여 장력을 해석한 결과는 실험 및 다른 계산과 유사한 결과를 보여주고 있다. 이는 스프링으로 텐돈을 가정한 것이 장력의 응답을 구하는데 유용하게 이용될 수 있는 것을 의미한다.
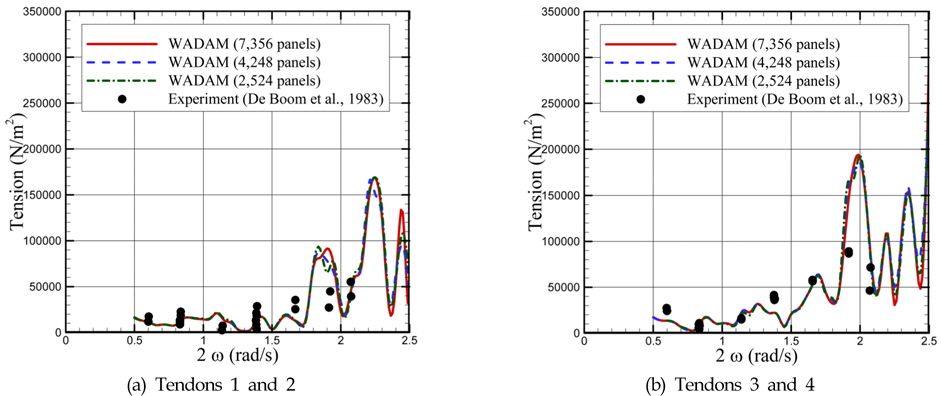
비선형 장력의 계산을 위하여, 규칙파 중에서 2차의 합주파수에 대한 장력의 응답을 계산하였다. Fig. 3은 선수파에서 계산한 비선형 장력 응답을 보여주는데, 패널수를 달리하면서 수렴도를 같이 확인하였다. 반폭 기준으로 7,356개의 패널을 사용하기까지도 계산 결과는 완전히 수렴하지는 않았으며, 패널 수의 변화에 비해 수렴도가 느리게 변하는 양상을 보여주고 있다. 2차의 전달함수는 직접 적분을 이용하여 경계조건방정식을 풀게 되는데, 이를 이용한 비선형 전달함수의 계산은 수렴이 느리다는 것이 많이 알려져 있다(Chen, 2007; Pan et al., 2013). 따라서 2차의 합주파수 거동을 계산하는 것도 수렴성에 대한 엄밀한 검증이 필요하다. 실험과의 비교에서는 계산이 유사한 결과를 보여주고는 있다. 그러나 장력이 크게 나타나는 지점에서는 실험 데이터가 부족하기 때문에, 온전한 경향을 파악하는 것은 다소 무리가 있다고 볼 수 있다. 결과를 살펴보면, 선형 장력에서와는 다르게 고주파에서 더 큰 응답이 나타나는 것이 특징이다.
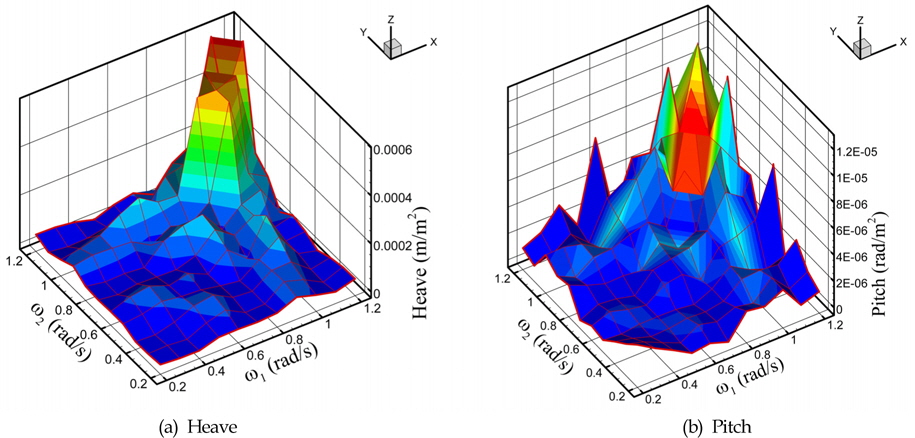
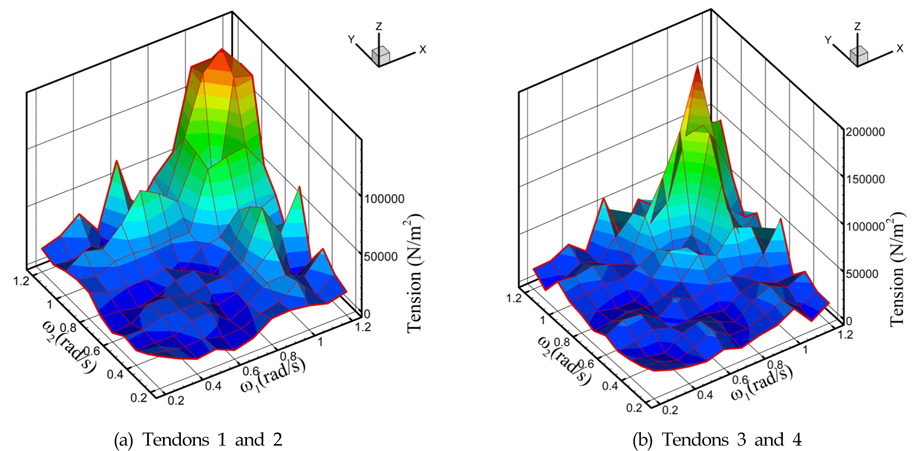
장력과 운동 응답의 관계를 파악하기 위하여 각각의 합주파 수 전달함수를 Figs. 4와 5에 나타내었다. 상하운동(Heave)과 종동요(Pitch)의 응답은 두 주파수의 합이 커지는 고주파 구간에서 큰 응답을 보여주고 있다. 이는 두 운동의 공진점이 고주파에 위치하기 때문에, 두 고주파의 조합이 공진에 가까워지면서 운동 응답이 더 커지고 있는 것을 의미한다. 장력은 텐돈이 부착되는 위치의 거동과 관련이 있기 때문에, 두 운동의 2차 전달함수와 거의 같은 경향을 보여주고 있다.
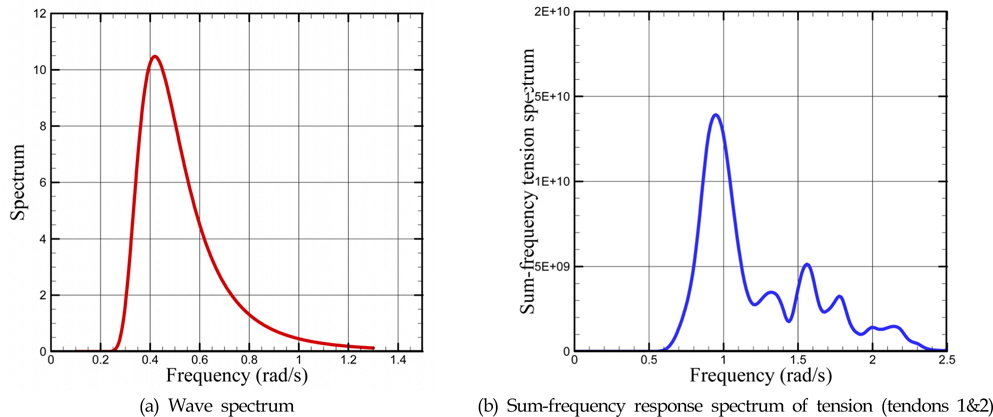
장력의 통계적 거동 파악을 위하여 식 (1)로부터 합주파수 스펙트럼을 계산하였으며 이를 Fig. 6에 나타내었다. 파는 Bretschneider 스펙트럼을 이용하였으며, 유의파고(
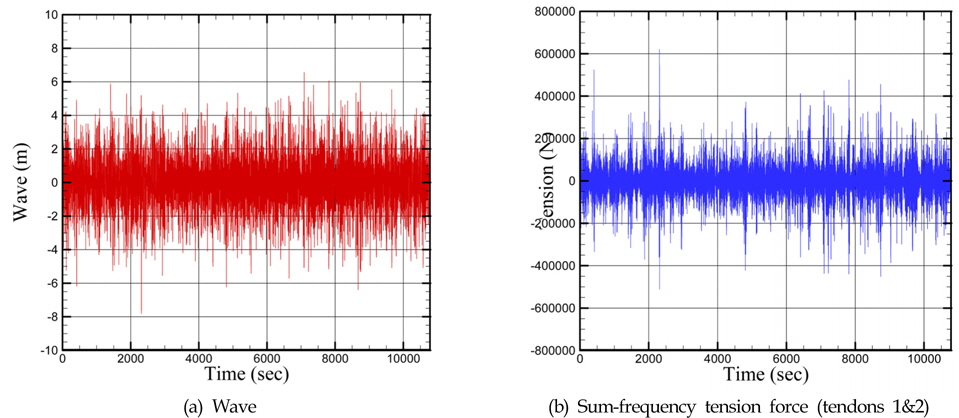
장력의 표준편차를 3가지 다른 방법으로 계산하여 비교하였다. 우선 응답의 스펙트럼으로부터 식 (2)를 이용할 수 있으며, 고유치 해석을 통하여 식 (7)을 이용할 수도 있다. 마지막으로 생성된 Fig. 7의 시계열로부터 표준편차를 직접 계산할 수 있다. Table 2는 3가지 방법으로 구한 장력의 표준편차를 나타낸 것으로 모두 유사한 결과를 보여준다. 이는 피로 파괴 및 통계적 거동 파악을 목적으로 한다면, 합주파수 스펙트럼과 고유치 해석을 이용하는 두 방법이 모두 효과적으로 적용될 수 있는 것을 보여준다.

Comparison of standard deviation of sum-frequency tension force from 3 different approaches (Hs=7m, Tp=15sec, tendons 1&2)
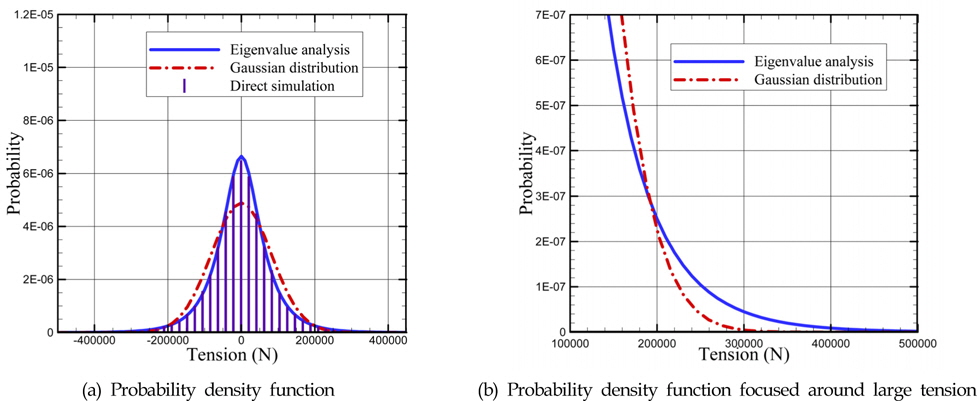
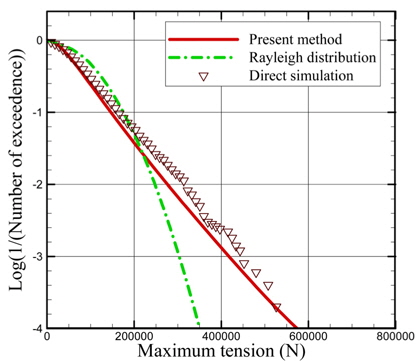
다음으로 실제 설계에 반영할 필요가 있는 극한의 장력을 계산하였다. 스프링잉의 확률밀도함수가 정규분포와는 다르기 때문에, 극한 해석 또한 일반적인 선형 운동과는 다른 접근이 필요하다. 장력의 최댓값을 구하는 방법으로 파의 통계적 거동에서 최댓값을 구하는 과정을 스프링잉에 적용하였다. 식 (10)을 이용하여 장력의 Peak에 대한 누적확률밀도함수를 계산하였고, 이를 발생빈도에 대한 함수로 Fig. 9에 나타내었다. 비교를 위하여 생성한 시계열(Fig. 7b)에서 Zero-crossing peak을 추출하여 그 분포함수를 같이 나타내었다. 현재의 방법이 예측하는 장력의 최댓값은 직접 추출한 peak과 유사한 경향을 보여주고 있다. 이는 본 연구에서 사용하는 간략한 계산을 통하여 장시간의 계산에서 나타날 수 있는 최대 장력을 빠르게 계산할 수 있는 것을 보여준다. 예측 결과를 비교하기 위하여, 선형 운동의 최댓값을 해석하는데 쓰이는 Rayleigh 분포를 같이 나타내었다. 스프링잉이 야기하는 장력의 최댓값은 설계의 기준이 되는 기간이 길수록 Rayleigh분포와는 차이가 커지는 것을 확인할 수 있다.
본 연구에서 적용한 기법은 주파수 영역의 해들을 이용하여 간단한 계산으로 장력의 최댓값을 예측할 수 있는 방법이다. 따라서 설계 해역의 방대한 해역의 환경 조합이 주어졌을 때에도, 이를 모두 고려하여 빠르게 설계 장력을 해석할 수 있다. 극한의 환경 조건에서 엄밀하게 비선형 거동을 파악하기 위해서는 복잡한 시간 영역 해석이 필요한데, 이전 단계로서 장력의 크기를 빠르게 예측할 수 있는 것이 본 연구의 장점이 될 수 있다.
본 논문에서는 TLP의 비선형 스프링잉 거동을 해석하여 장력의 통계적 특성을 파악하였으며, 장력의 최댓값을 예측할 수 있는 기법을 연구하였다. 본 연구를 통하여 다음의 결론을 얻을수 있다.
(1) 스프링잉으로 인한 TLP의 운동 및 장력의 통계적 거동은 정규분포를 벗어난다. 고유치 해석을 이용하여 스프링잉에 적합한 확률밀도함수를 계산하였고, 이를 통해 스프링잉은 과도한 장력이 정규 분포보다 높은 확률로 나타나는 것을 확인하였다.
(2) 극한의 장력을 해석하기 위하여 peak의 분포를 스프링잉의 확률밀도함수에서 계산하는 방법을 제안하였다. 이 기법은 시계열을 생성하여 비교한 장력의 peak과 유사한 결과를 보여주었다.
(3) 본 연구에서 소개하는 기법은 주파수 영역의 해를 이용하여 스프링잉으로 인한 TLP의 장력을 빠르게 예측할 수 있게 해준다. 따라서 이 기법은 실제 해역의 방대한 환경 조합에서 위험한 조합을 빠르게 찾는 과정에 이용될 것으로 기대할 수 있다.