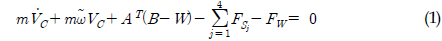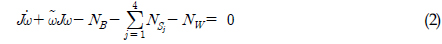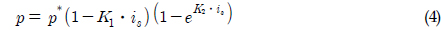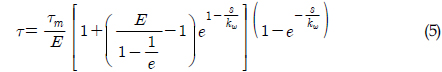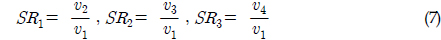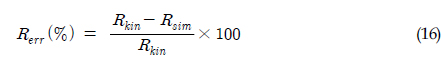This paper considers the steering characteristics of a four-row tracked vehicle crawling on extremely cohesive soft soil, where each side is composed of two parallel tracks. The four-row tracked vehicle (FRTV) is assumed to be a rigid body with 6-DOF. A dynamic analysis program for the tracked vehicle is developed using the Newmark-𝛽 method based on an incremental-iterative scheme. A terra-mechanics model of an extremely cohesive soft soil is implemented in the form of the relationships of the normal pressure to the sinkage, the shear resistance to the shear displacement, and the dynamic sinkage to the shear displacement. In order to investigate the steering characteristics of the four-row tracked vehicle, a series of dynamic simulations is conducted with respect to the distance between the left and right tracks (pitch), steering ratios, driving velocity, reference track velocity, lengths of the tracks, and properties of the cohesive soft soil. Through these numerical simulations, the possibility of using a kinematic steering ratio is explored.
육상광상에 비해 니켈, 코발트, 구리의 함량이 대단히 높은 심해저 망간단괴는 수심 3000∼5000m의 전 세계 심해저에 널리 분포되어있는 대표적인 심해저 광물자원이다. 특히, 태평양의 클라리온-클립퍼톤 해역(CCFZ: Clarion-clipperton fracture zone)에 부존되어 있으며, 막대한 양의 망간단괴는 세계 선진각국의 상업적 개발의 목표가 되고 있다.
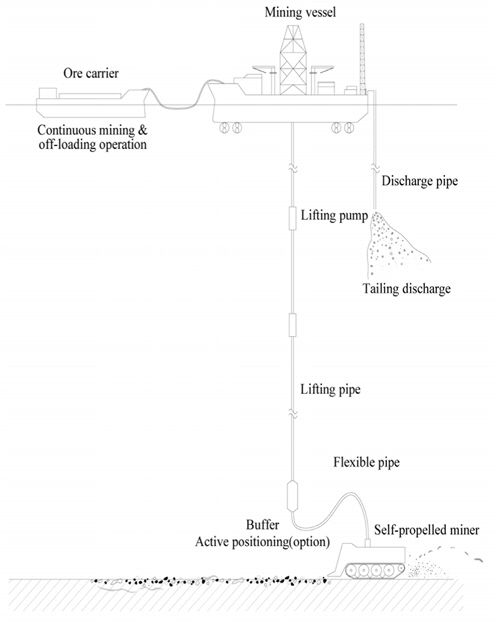
심해저의 퇴적지반은 매우 높은 함수율을 가지는 미세한 입자들로 구성되어 지반의 지지력(Bearing capacity)이 매우 미약하다는 문제점을 가진다. 이러한 미약한 지반 지지력으로 인해 상업생산에 요구되는 시간당 최대 500톤에 달하는 망간단괴를 집광시스템으로 실어 운반하는 것은 불가능하며, 해상의 채광선까지 양광관을 통하여 연속적으로 채광하는 것(Continuous mining, Fig. 1 참조)이 필요하다(Brink and Chung, 1981; Hong and Kim, 1999). 연속적 채광시스템은 Fig. 1처럼 해상의 채광선, 양광관, 중간버퍼, 유연관, 자주식 집광로봇으로 구성되어 있다.
자주식 집광로봇은 해저면을 주행하면서 해저면 바닥에 있는 망간 단괴를 채집한다. 해저면에 분포해 있는 망간단괴를 채집하기 위해서는 집광로봇의 침하가 적게 발생하는 것이 망간단괴의 채집효율을 높일 수 있으며, 또한 선회반경이 작으면 작을수록 주행경로를 최적화 할 수 있다.
심해저 연약지반을 주행하는 집광로봇은 지면과 접촉하는 지점에서의 접지압을 낮추기 위해 접지 면적이 넓은 폭이 큰 궤도를 사용하고 있다. 하지만 폭이 큰 궤도의 사용으로 인해 궤도의 변형이 발생할 수 있다. 또한 집광로봇의 채집용량을 증가시키기 위해서 여러 개의 채집장치를 집광로봇의 전면부에 병렬로 장착해야 한다. 이러한 경우 채집장치를 장착할 수 있는 공간 확보 및 구조적인 안정성을 높여야 하며, 이를 위해 좌 /우 양쪽 궤도를 2열로 분리한 4열 무한궤도 차량(Four-row tracked vehicle, FRTV)이 제안되었다(Hong et al., 2011). 4열 무한궤도 차량은 좌/우 각각의 궤도 시스템이 2개의 궤도로 이루어져 있으며, 4개의 궤도는 독립적인 구동이 가능하도록 되어 있다.
하지만 4열 무한궤도 차량의 운용에 있어, 직진의 경우에는 일반 2열 무한궤도 차량과 큰 차이점을 보이지 않지만, 선회의 경우에는 많은 차이점을 가지고 있다. 일반적으로 자동차의 경우, 차량의 조향각을 이용하여 조향을 하지만, 궤도차량의 조향은 좌, 우 궤도의 속도차이를 이용한다. 하지만 4열 무한 궤도차량의 경우, 궤도가 4개인 관계로 좌우 궤도의 속도차를 이용하여 조향을 하기에는 어려운 문제점이 발생한다. 그리고 궤도가 4개인 관계로 각각 궤도의 속도에 따라 어떤 궤도는 견인력 (Traction force)을, 또 다른 어떤 궤도는 저항력(Braking force)을 가지게 된다.
이러한 문제점을 해결하기 위해 본 논문에서는 각각 궤도의 속도에 따른 선회성능을 분석하고, 이를 활용하여 궤도의 선회반경에 따른 최적 선회비를 도출하고자 한다. 최적 선회비 도출에는 선회반경과 주행차량의 정적 평형식을 사용하였다.
4열 무한궤도 차량의 선회특성을 분석을 위한 수치해석 프로그램은 Hong et al.(2002) 및 Kim et al.(2006)에 의해 개발된 연약지반 강체 주행차량의 동적거동 해석 프로그램을 확장하였으며(Lee et al., 2009; Kim et al., ,2010), 수치해석 시적분에는 Newton 방법과 Newmark 시적분법을 통합한 미소증분 반복계산 알고리듬이 사용되었다. 4열 무한궤도 차량 비선형 동력학 해석 프로그램은 FORTRAN으로 개발되었으며, 연약지반에 대한 지반주행역학 모델을 포함시켰다.
선회성능 분석을 위한 입력변수는 궤도사이의 피치, 조향비, 차량의 속도 등이 사용되었다.
무한궤도 차량의 동적거동 해석은 크게 다물체 모델과 강체 모델로 나눌 수 있다. 다물체 모델은 실제모델과 유사하도록 각각의 구성요소를 모델링하는 반면에 강체 모델은 실제모델을 하나의 강체로 모델링하는 것을 의미한다.
다물체 모델의 장점은 차량의 각 요소의 세부적인 모델링을 바탕으로 각 요소에 대한 동적 거동 특성의 예측이 가능하다는 점과, 이러한 동적 거동 특성을 통하여 세부설계 제작에 매우 유용하게 사용될 수 있다는 점이다. 하지만 다물체 모델 생성을 위해서는 많은 수의 강체와 구속조건 등을 사용함으로써, 모델의 자유도(Degree of freedom)가 크게 증가하게 된다. 자유도의 증가로 인하여 풀어야 할 방정식의 수가 늘어남으로써 수치해석에 매우 긴 시간이 소요된다.
이와 반대로 강체모델은 실제모델을 하나의 강체로 가정하여 모델링하기 때문에 다물체 차량 해석에서 발생하는 수치해석 시간의 문제를 해결할 수 있다. 하지만 강체 차량 모델은 실제모델을 단일 강체로 모델링함으로써 실제 발생할 수 있는 다물체적 운동에 대한 지나친 단순화에 따른 해석 결과의 적용 제한조건이 크며, 동시에 해석결과의 신뢰를 얻기 위한 충분한 검증작업을 필요로 한다.
Kim et al.(2003)은 점착성 연약지반 무한궤도 차량을 이용하여 다물체 모델과 강체 모델의 동적거동 해석 결과를 비교.검증한 바 있다.
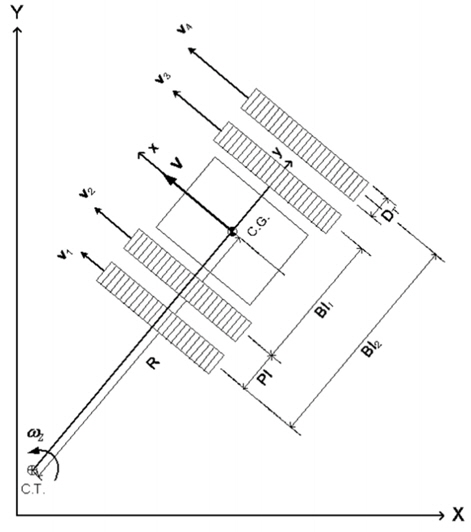
Fig. 2는 4열 강체 무한궤도 차량의 개념도를 나타내고 있다.
4열 무한궤도는 차량의 좌우에 궤도가 각각 2개씩 병렬로 배열되어 있다. 각각의 궤도는 스프라켓을 가지고 있어 독립적인 구동이 가능하다.
차량 고정 차량 고정 좌표계 대한 강체 주행차량의 운동방정 식은 다음과 같이 구해진다(Hong et al., 2002).
여기서
~기호를 tilde(~)라고 부르며, 는 벡터
차량의 무한궤도와 토양의 접촉에 따른 지반반력은 토양의 수직응력과 전단응력으로 나눌 수 있다(Hong et al., 2002). 토양의 수직응력은 차량의 지면 압력으로 표시되고, 압력-침하간 의 관계식에 의해 얻어지며, 전단응력은 차량의 궤도와 접촉하는 지면의 전단변위를 통해 구할 수 있다.
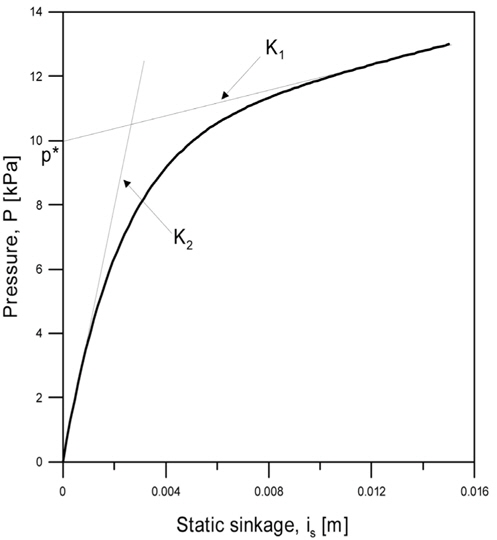
차량의 자중에 의한 수직응력은 정적침하의 함수로 표시되며 다음과 같이 표현된다(Bode, 1991).
여기서
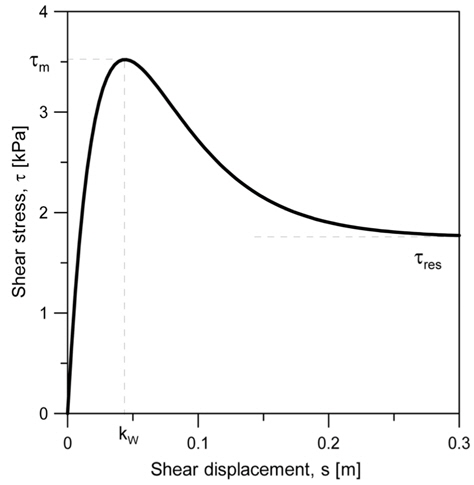
연약한 점착성 토양은 Fig. 4와 같이 일정 이상의 전단변위가 발생하면 토양이 급격히 붕괴되는 전형적인 비선형성을 나타낸다(Hong and Choi, 2001). Wong (1993)은 이러한 점착성 토양의 전단응력을 다음과 같은 함수로 제안하였다.
여기서, 𝜏
토양의 전단변위는 부가적인 동적침하(Slip sinkage)를 발생시키는데, 그 표현은 다음과 같다.
여기서,
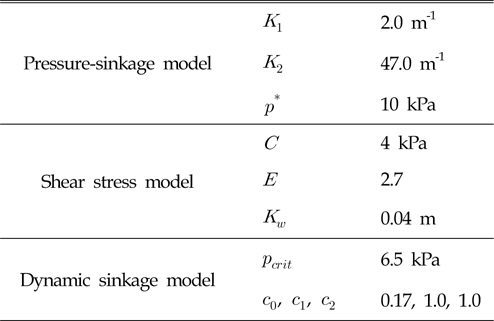
Hong and Choi(2001)은 물과 벤토나이트를 혼합하여 해저연약지반을 모사하였으며, 식 (4)~(6)의 계수들은 침하 실험 및 견 인력 실험을 통하여 구하였다. 본 논문에서 사용된 점착성 토양모델에 대한 계수는 Table 1에 나타나 있다.
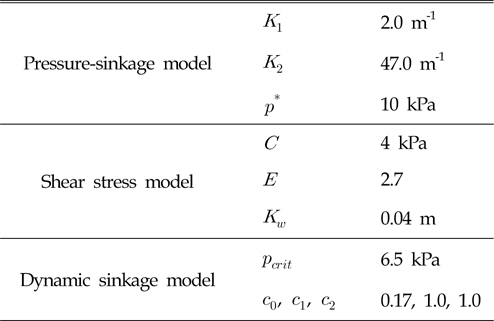
Data of soil model
4열 무한궤도 차량의 선회 성능을 분석하기 수치 시뮬레이션을 수행하였다. 수치 시뮬레이션에 사용된 조건은 다음과 같다.
■ 궤도사이의 피치(PI) : 1.0DT, 1.5DT, 2.0DT, 2.5DT, 3.0DT, 3.5DT, 4.0DT, ■ 선회비(SRi ) : 1.1, 1.2, 1.3, 1.4, 1.5 ■ 기준 궤도 속도(v1) : 0.5(m/s)
여기서 궤도 사이의 피치(
선회비는 다음과 같이 기준 궤도 속도에 대한 각각의 궤도 속도에 대한 비를 의미한다.
여기서
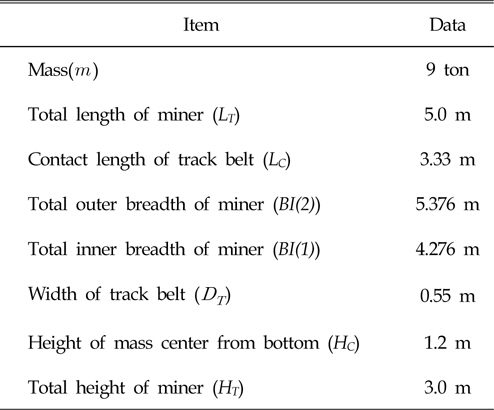
해석에 사용된 차량 모델의 제원은 Table 2에 나타나 있다.
[Table 2] Principal dimensions of miner model
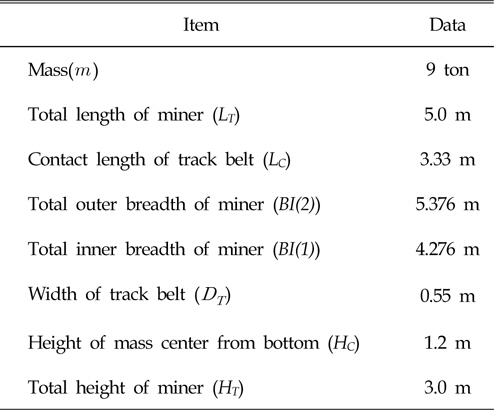
Principal dimensions of miner model
4.1절의 시뮬레이션 조건을 이용하여 수치해석을 수행하였다. 수치해석의 결과를 통해 4열 무한궤도 주행차량의 선회특징을 분석하였다. 선회성능을 분석하기 위해 다음과 같은 방법을 사용하여 선회반경을 계산하였다.
■ R=v/w ■ 3점을 이용한 원의 방정식
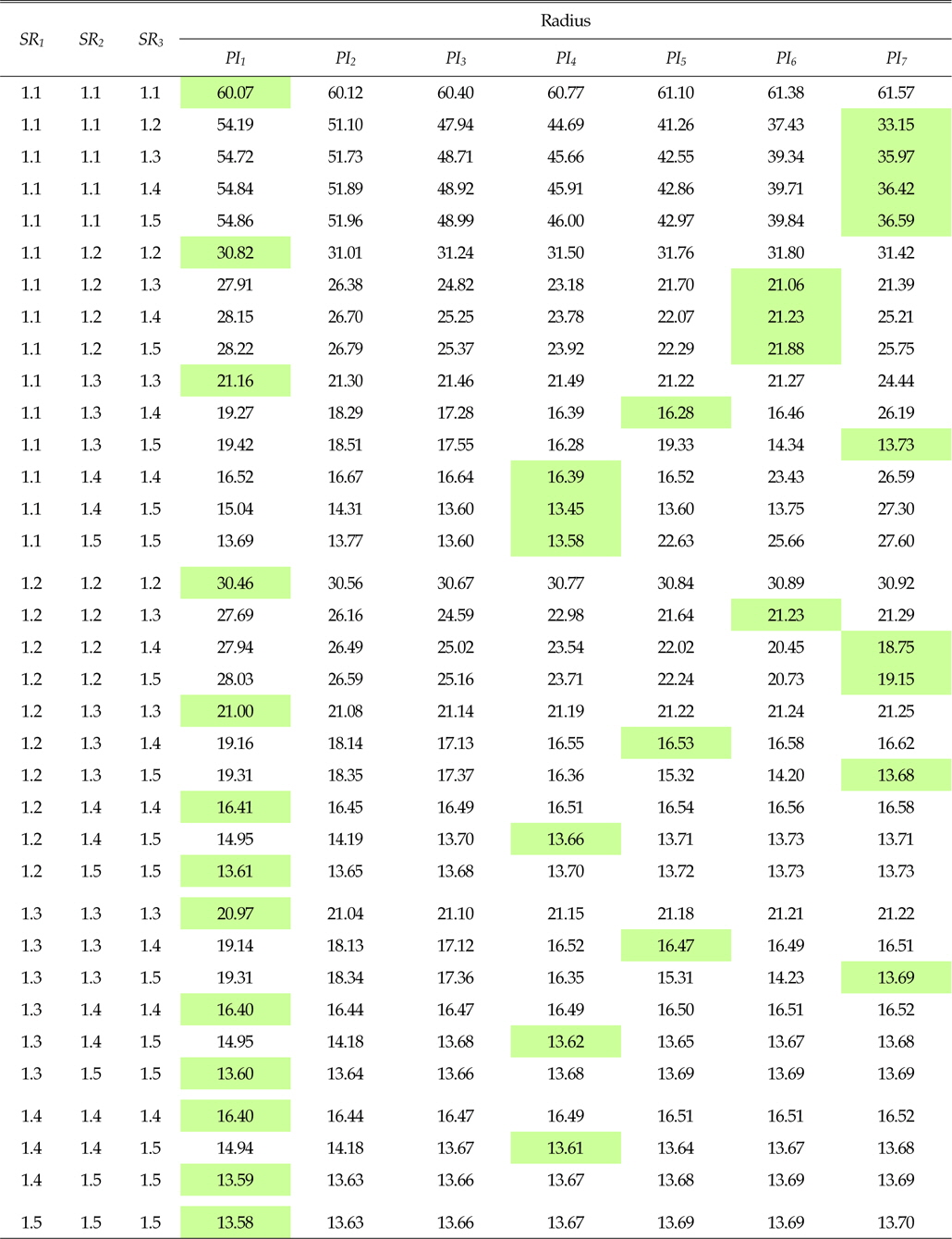
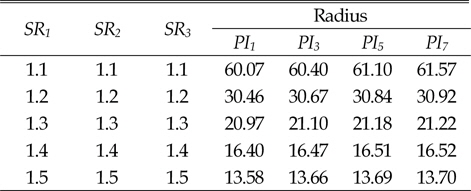
Table 3은 시뮬레이션 결과 중 선회비와 피치의 변화에 따른 선회반경의 일부분을 나타내고 있다. 해석의 결과 분석을 통하여 4열 무한궤도 차량의 선회성능에 대해 다음과 같이 요약을 할 수 있다.
[Table 3] Turning radius w.r.t. pitch and steering ratio
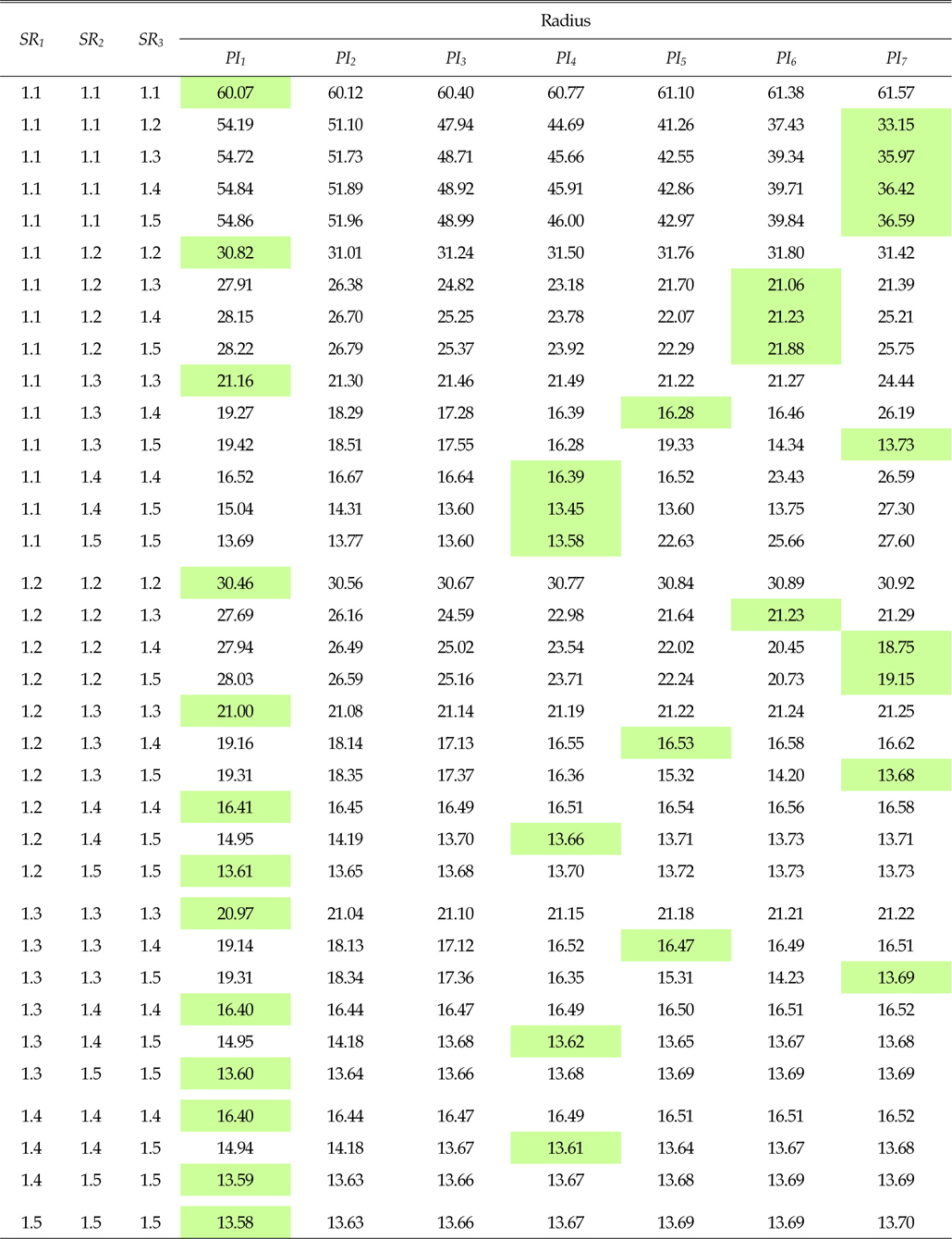
Turning radius w.r.t. pitch and steering ratio
(1)
■선회비가 증가하면 선회반경은 작아진다. ■피치가 증가하면 선회반경이 증가하나, 그 변화량은 매우 작다.
(2)
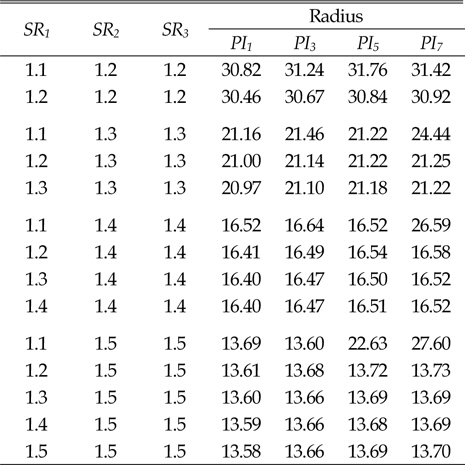
■선회비가 증가하면 선회반경은 작아진다. ■SR1은 선회반경에 거의 영향을 미치지 않는다. ■피치가 증가하면 선회반경이 증가하나, 그 증가량은 매우 작다.
(3)
■SR3가 SR2와 같은 경우를 제외하고는 SR3의 변화에 대해 선회반경은 거의 변하지 않는다.
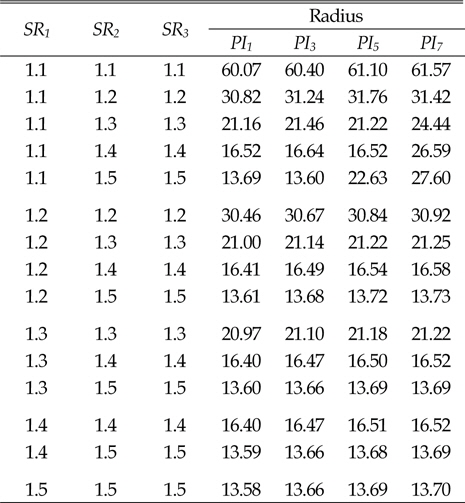
[Table 4] Turning radius of case 1
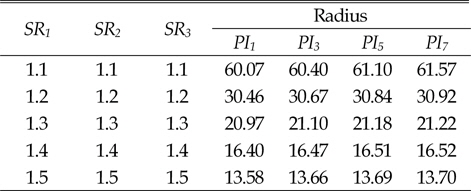
Turning radius of case 1
[Table 5] Turning radius of case 2
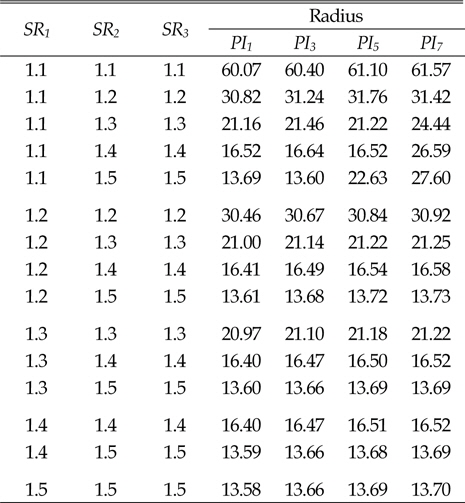
Turning radius of case 2
[Table 6] Turning radius of case 3
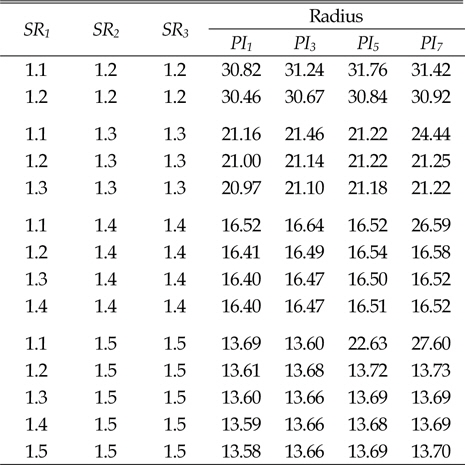
Turning radius of case 3
이상의 결과에서 보듯이 4열 무한궤도 차량에서도 선회비가 큰 경우 선회반경이 작아지는 것을 알 수 있다. 하지만 3번의 경우처럼 선회비가 증가하더라도, 선회반경이 거의 변하지 않는 것을 확인할 수 있다. 이러한 경우, 차량의 선회비의 증가에 의해 차량의 조향성능은 아무런 변화가 없고 오히려 차량의 침하를 증가시켜 전체적인 차량의 주행성능에 좋지 않은 영향을 미친다.
이러한 문제점을 해결하고, 차량의 선회성능을 향상시키기 위해, 선회반경에 대한 최적 선회비를 찾는 것이 필요하다. 본 논문에서는 주행차량의 기구학적 특성을 이용하여 최적 선회비를 찾고자 한다.
차량의 기구학적 관계식을 이용한 최적 선회비를 찾기 위해 다음과 같은 가정을 사용하였다.
■ 4열 무한궤도 주행차량은 지면에 대해 평면운동을 한다. ■ 각각의 무한궤도 속도는 작은 것으로 가정한다. 즉, 지반의 슬립이 거의 발생하지 않는 것으로 가정한다. ■ 주행차량의 순간회전 중심과 차량의 무게중심은 일치한다.
상기의 가정을 적용하며, 주행차량의 선회반경은 다음과 같이 정의할 수 있다.
여기서,
기구학적 관계식을 이용하여, 각각의 궤도의 속도를 구하면 다음과 같이 표현된다(참조 Fig. 2).
여기서,
식 (9)~(12)를 이용하여, 식 (7)의 선회비를 다시 계산하면 다음과 같이 표현된다.
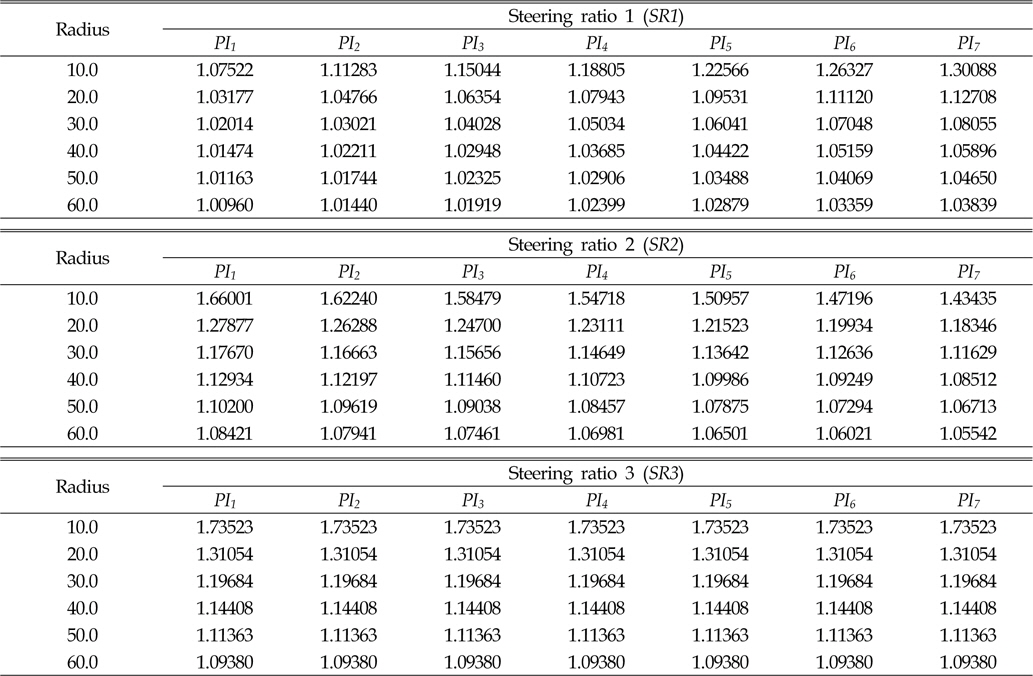
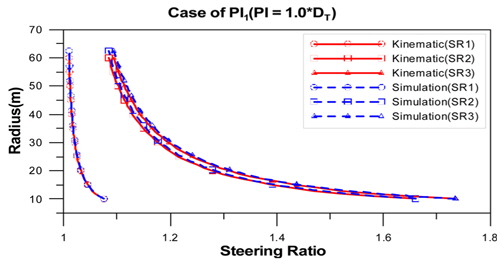
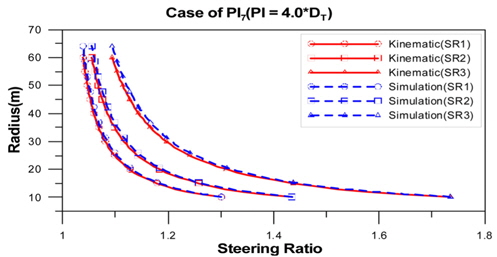
이상과 같이, 주행차량의 선회비를 차량의 속도가 아닌 차량의 기구학적 관계식으로만 표현을 하였다. 식 (13)~(15)을 이용하여 선회반경에 따른 궤도차량의 선회비를 계산하였다(Table 7).
[Table 7] Kinematic steering ratio
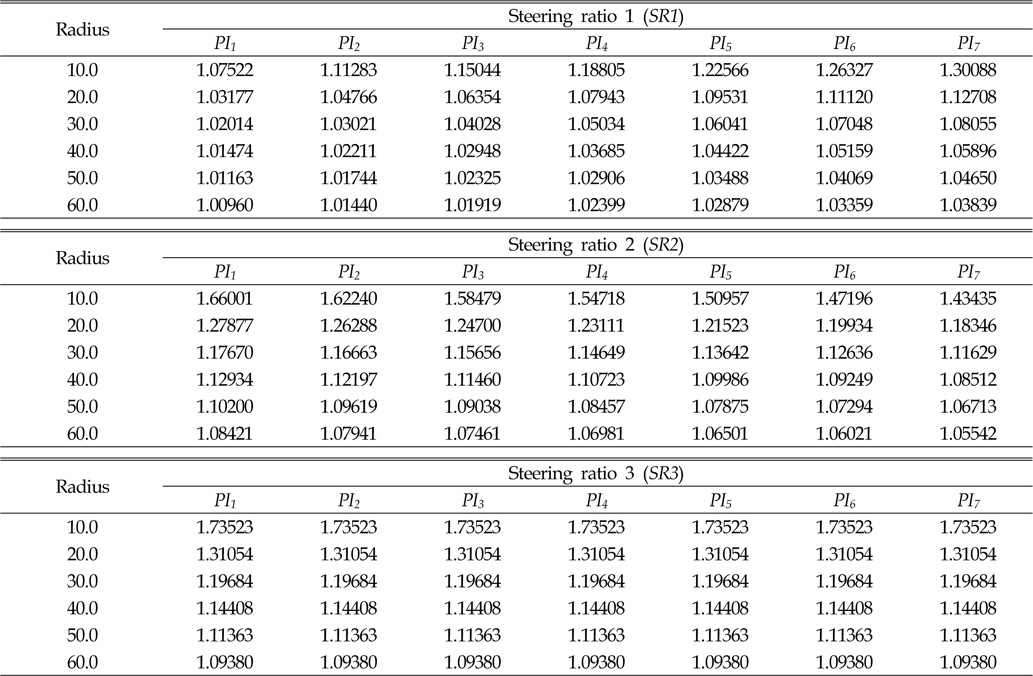
Kinematic steering ratio
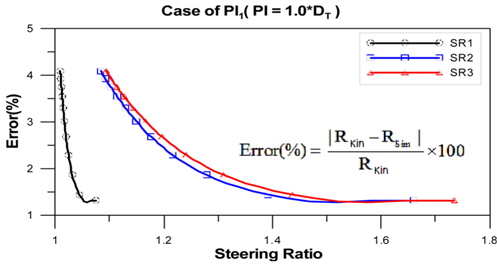
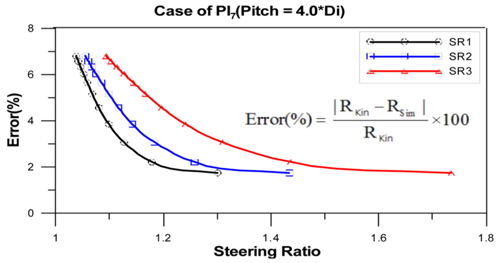
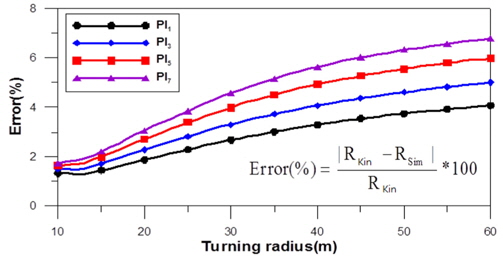
계산된 선회비의 적합성을 판별하기 위해, 선회비에 따른 주행차량의 동적거동 해석을 수행하였다. 기구학적 관계식에 사용된 선회반경과 실제 해석 결과에서 구해진 선회반경에 대해 식 (16)과 같이 상대 오차를 구하여 제안된 선회비에 대한 검증을 수행하였다.
여기서,
Fig. 5~.8에서 보는바와 같이, 선회비가 증가함에 따라 상대적인 에러(
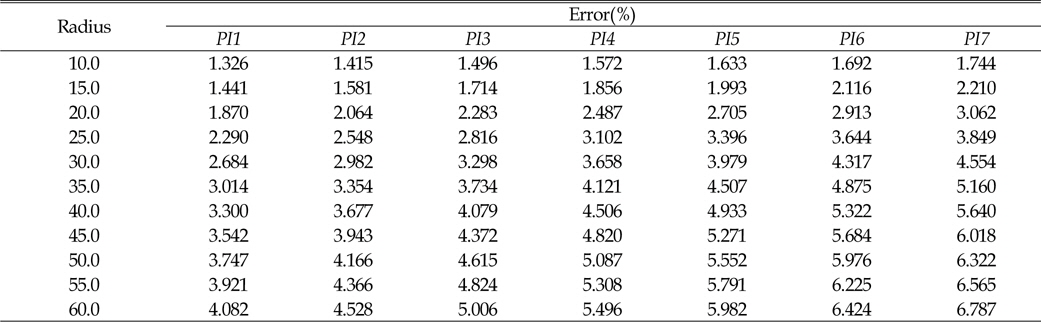
[Table 8] Error of turning radius with respect to PI and turning radius
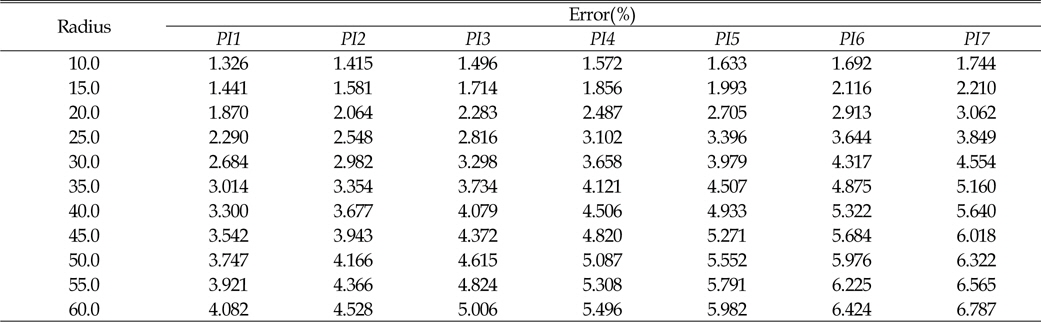
Error of turning radius with respect to PI and turning radius
본 논문에서는 연약지반 모델이 적용된 4열 무한궤도 차량의 선회성능에 대한 해석을 수행하였다. 수치해석을 통하여 다음과 같은 결론을 도출하였다.
(1) 궤도의 피치가 증가하면 선회반경이 증가하나 증가량은 아주 작다
(2) 기구학적 관계식에 의해 도출된 선회비를 통한 선회반경은 선회반경이 증가할수록 선회반경의 에러가 증가하였으나, 선회반경이 60m인 경우에도 선회반경에 대한 상대적인 에러가 7%이내였다.
(3) 기구학적 관계식을 이용한 선회비를 4열 궤도 주행차량의 최적 선회비로 정의가 가능하였다.