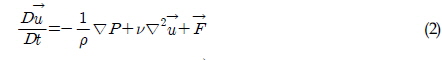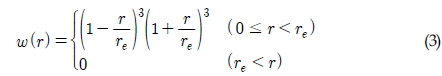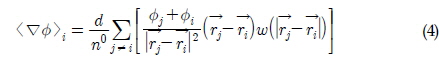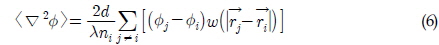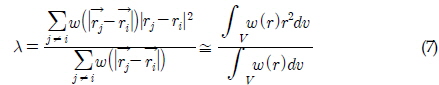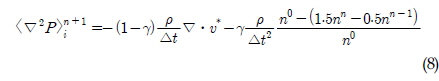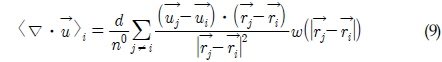The incident bore impact loads acting on a tall structure is simulated using the refined Moving Particle Simulation (MPS) method. The particle method is more feasible and effective than conventional grid-based methods for the violent free-surface problems. In the present study, the simulation results for the temporal change of the hydrodynamic force on the structure and longitudinal velocity component around the structure are compared with the experiments (Radd and Bidoae, 2005). And the mitigation effects by installation of various obstacles in front of the main structure are investigated and discussed form the simulation results.
지진해일(Tsunami)은 해저에서의 지진, 해저 화산 폭발, 단층 운동 같은 급격한 지각 변동이나 빙하의 붕괴, 핵실험 등에 의해 발생하는 파장이 긴 천해파를 말한다. 지진해일의 초기 파고는 약 0.5~1.0m에 불과하지만 그 파장은 수심에 비해 아주 길어 100~150km에 달하고 심해역에서는 파장의 전파 속도가 700~1000km/h에 달한다. 심해역에서 발생한 지진해일은 처음에는 빠르게 전파되며 연근해역에 접근하면서 수심의 급격한 감소로 인해 파형은 급준화되고 전파속도는 감소하게 된다. 천수해역인 해안, 만, 항구 등에 도달하는 시점에는 전파되는 파랑의 에너지가 급준화된 파정 부근에 집중하고 경우에 따라서는 파고가 수십 미터 이상이 되어 인근의 구조물이나 어장 등 인간의 생활환경에 큰 피해를 준다. 따라서 지진해일에 대한 정확한 예측과 피해를 최소화할 수 있는 방재 시스템의 구축이 필요하다.
해안 근처에 작용하는 지진해일의 거동은 비선형성이 강한 자유표면 유동과 유체의 분열 및 합체를 동반한다. 따라서 입자를 사용하는 입자법은 격자를 생성할 필요가 없어 쇄파나 2상류등과 같이 복잡한 물리현상을 해석하고 공학적인 문제 적용에 보다 유연하다고 할 수 있다. 특히, 입자법은 이류항(Convection)의 계산을 완전한 라그란지(Lagragian) 접근에 의해 입자의 이동으로 직접 계산함으로서 격자기반의 오일러(Eulerian) 접근법에서 심각하게 유발되는 수치 확산이 없을 뿐 아니라, 질량이 완벽히 보존된다는 장점을 가지고 있다. 또한 격자가 꼬이는 등의 위상관계(Topological relations)를 고려할 필요가 없다. 대표적인 입자법으로는 Monaghan(1988)이 제안한 SPH(Smoothed particle hydrodynamics)법과 Koshizuka and Oka(1996)가 제안한 MPS(Moving particle simulation)법이 있다. MPS법은 미분연산을 위해 커넬함수 기반의 차분 알고리즘을 사용하고 있지만, SPH법에서는 커넬함수가 직접 미분된 형태의 방정식을 사용하고 있다. MPS법의 경우 SPH법에 비해 경사 모델의 정확도가 높고 또한 비압축성 유동 해석에 보다 뛰어나다는 장점을 가지기고 있다.
본 논문에서는 MPS법을 개량한 PNU-MPS(Pusan national university modified-MPS) 법(Lee et al., 2011)을 기본으로 국소지역에서 지진해일과 같은 너울성 단일 대형 파랑이 연안구조물에 작용하는 3차원 유동장을 수치모사(Numerical simulation)하고, 구조물에 작용하는 파력과 전진속도를 Radd and Bidoae(2005)의 실험 결과와 비교하였다. 또한 연안구조물 주변에 부가구조물(Obstacles)을 설치하여 이에 따른 파랑 충격 완화 효과에 대해서 수치모사하고, 완화 효과에 따른 유체력과 유동장 특성에 대하여 비교·분석하였다.
비압축성 점성 유동에 관한 지배방정식은 연속 방정식과 Navier-Stokes 방정식이다.
여기서
비압축연속방정식 (1)은 격자법에서는 통상적으로 속도의 발산(Divergence)으로 표현되는 반면, 입자법에서는 밀도에 관한식으로 표현된다. Navier-Stokes 방정식 (2)의 좌변은 이류항을 포함한 라그란지의 전미분(Total derivative) 형태이고, 이는 입자의 직접적인 이동에 의해 계산된다. 한편, 우변은 압력 경사항, 점성항 그리고 외력항으로 구성되어 있다. 비압축성 점성 유동을 시뮬레이션하기 위해서 지배방정식의 편미분 연산자를 포함하는 모든 항은 MPS법(Koshizuka and Oka, 1996)의 상호작용 모델에 의해 치환되어야 한다. 본 연구에서는 원래의 MPS법(Koshizuka and Oka, 1996)을 개량하여 정확도와 안정성을 향상시킨 PNU-MPS법(Lee et al., 2011)을 도입하여 입자간 상호작용 모델로 치환하기로 한다. 비압축연속방정식 (1)은 격자법에서는 통상적으로 속도의 발산(Divergence)으로 표현되는 반면, 입자법에서는 밀도에 관한 식으로 표현된다. Navier-Stokes 방정식 (2)의 좌변은 이류항을 포함한 라그란지의 전미분(Total derivative) 형태이고, 이는 입자의 직접적인 이동에 의해 계산된다. 한편, 우변은 압력 경사항, 점성항 그리고 외력항으로 구성되어 있다. 비압축성 점성 유동을 시뮬레이션하기 위해서 지배방정식의 편미분 연산자를 포함하는 모든 항은 MPS법(Koshizuka and Oka, 1996)의 상호작용 모델에 의해 치환되어야 한다. 본 연구에서는 원래의 MPS법(Koshizuka and Oka, 1996)을 개량하여 정확도와 안정성을 향상시킨 PNU-MPS법(Lee et al., 2011)을 도입하여 입자간 상호작용 모델로 치환하기로 한다.
연속적인 유체의 흐름은 입자의 속도성분, 질량, 압력과 같은 물리량으로 나타낼 수 있으며, 입자들의 상호작용 움직임에 의해 가시화 되므로 편미분 형태의 지배 방정식은 입자간 상호작용 방정식으로 변환된다. MPS법에서 입자 상호작용은 커넬 함수에 기초하여 이루어져 있다. 본 연구에서 사용한 커넬 함수의 구체적인 식은 식 (3)과 같다.
여기서
PNU-MPS 법에서 입자
여기서
수학 연산자인 라플라시안(Laplacian, ∇ 2)은 물리적으로 확산을 의미하며, 입자
단, λ는 해석해와 동일한 분산을 유지하기 위해 사용하는 계수이다.
만약 입자의 질량이 모두 동일하다면, 유체의 밀도는 입자수 밀도에 비례하므로 연속방정식 식 (1)은 입자수밀도가 일정하다는 조건과 동일하다.
PNU-MPS법에서는 비압축성 유동의 계산 알고리즘으로서 SMAC(Simplified marker and cell)법과 거의 유사한 알고리즘을 사용한다. 매 시간 스텝은 양과 음의 2단계로 나눈다. 시각
제 2단계에서는 먼저 다음과 같은 압력의 포아송(Poisson)방정식을 음적으로 계산한다.
단, 우변의 상수 𝛾는 비압축성 조건을 만족하는 범위 내에서 1.0이하의 값이며, Lee et al.(2011)은 0.01<𝛾< 0.05의 값을 추천하고 있다. 본 연구에서는 수치적 실험을 통해 얻은 𝛾=0.01을 선택하였다.
식 (8)의 좌변은 확산 모델 식 (6)에 의해 연립 1차방정식으로 이산화 할 수 있으며, 적절한 반복해법에 의해 구할 수 있다. 또한, 식 (8)에서 우변의 첫 번째 생성항은 속도의 무발산 조건에 해당되며 다음 식을 이용하여 구할 수 있다.
그리고 식 (8)의 우변의 두 번째 생성항은 시뮬레이션이 수행되는 동안 입자수밀도가 일정하게 유지되어야 한다는 비압축성 조건을 만족시키는데 기여를 하게 된다.
압력이 구해진 뒤 식 (10)으로부터 속도의 수정치 를 계산한다. 이때 식 (10)의 우변의 압력 경사 계산은 경사 모델 식 (4)를 사용한다.
최종적으로 시각
자유표면 경계조건으로 운동학적(Kinematic) 경계조건과 역학적(Dynamic) 경계조건이 있다. PNU-MPS법에서 운동학적 경계조건은 자유표면 입자를 직접 이동하여 만족시키고, 역학적 경계조건은 자유표면 입자의 압력을 대기압과 동일한 0의 값으로 고정함으로써 만족시킨다. 두 경계조건을 만족시키기 위해서는 자유표면 입자의 탐색이 선행되어야 한다. 자유표면 입자의 탐색은 식 (13)와 (14)을 따른다.
여기에서
입자법 시뮬레이션에는 입자간의 상호작용에 충돌 모델을 사용하여 두 입자간 거리가 어느 이상으로 가까워 질 때 충돌로 인식하고 서로 척력을 발생시킨다. 하지만 충돌 모델이 없어도 계산에 지장이 없는 경우가 많다. 이는 충돌 모델이 없다고 하더라도 입자들이 서로 가까워지게 되면 국소적으로 압력이 높아져 입자들의 반발력이 발생하기 때문이다. 그러나 식 (13)와 (14)를 만족하는 입자는 자유표면 경계조건으로 압력이 대기압으로 고정되어 입자가 서로 가까워져도 압력이 높아지지 않는다. 입자들이 가까워짐에 따라 입자수밀도가 증가하여 자유표면 입자 판정법에 의해 자유표면 입자에서 제외되면 압력이 급격하게 높아지게 된다. 이러한 현상은 압력의 시간적·공간적 진동을 유발한다. 따라서, 충돌 모델의 도입으로 자유표면 근처에서 적절한 척력을 발생시켜 압력의 시간적·공간적 진동을 감소시킬 수 있다.
충돌 모델에서 충돌 기준이 되는 거리는 초기 입자간 거리
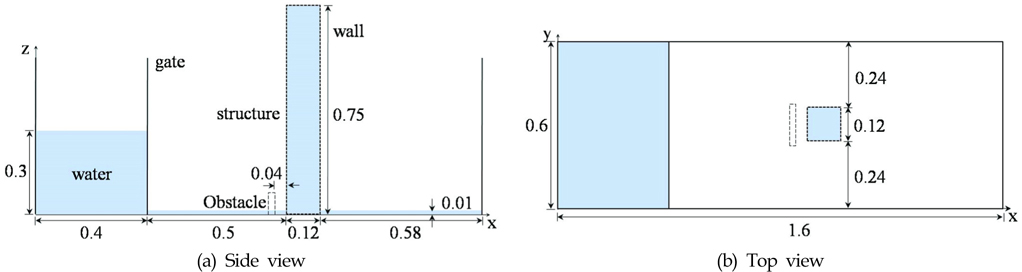
앞서 설명한 입자간 상호작용 모델을 이용하여 지진해일과 같은 단일 대형 붕괴파가 연안 구조물에 작용하는 충격 과정을 수치모사 하였다. Fig. 1과 같이, Radd and Bidoae(2005)의 실험과 동일한 조건으로 수치모사를 수행하였다. 본 절에서 다루는 문제에 대하여 Gómez-Gesteira and Dalrymple(2004)는 SPH법을, Radd and Bidoae(2005)는 ELMMC(Eulerian-Lagrangian marker and micro cell)법을, 그리고 Kim et al.(2007)은 Original MPS법을 각각 이용하여 수치적으로 모사한 바 있다.
사용된 수조의 크기는 길이, 너비, 높이가 1.6(m)×0.6(m)×0.75(m)이다. 초기 상태에서 단일 대형 파도는 댐붕괴로 인한 유입붕괴파(Incident bore wave)로 가정하였으며, 이때 댐 안에 갇혀 있는 물기둥의 크기는 0.4(m)×0.6(m)×0.3(m)이다. 수문은 시각
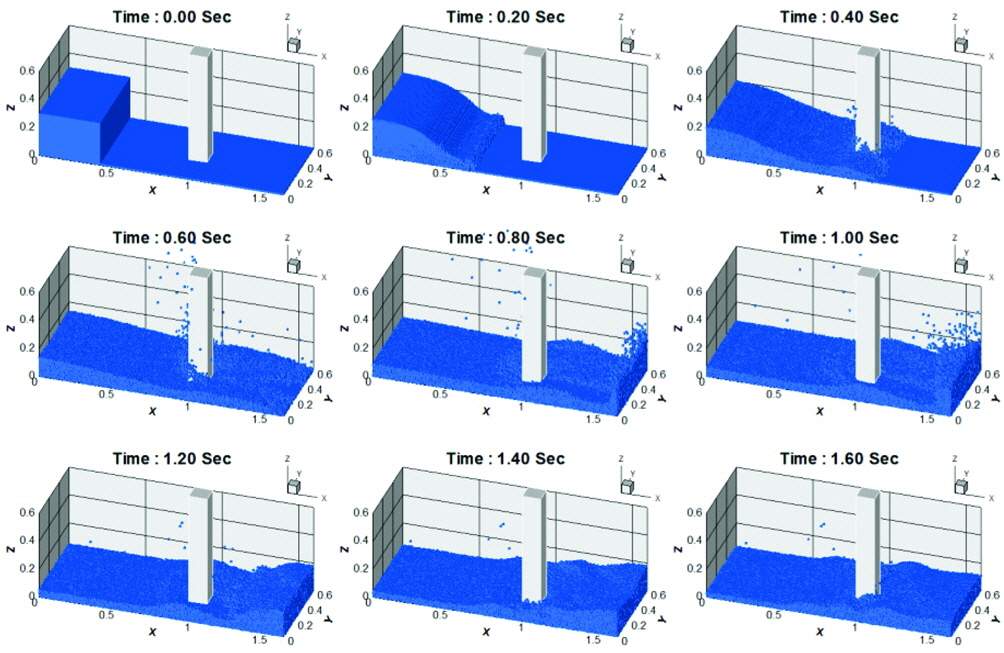
Fig. 2는 시간 변화에 따른 자유표면과 구조물의 상호작용에 관한 수치모사의 결과를 나타낸다. 시각
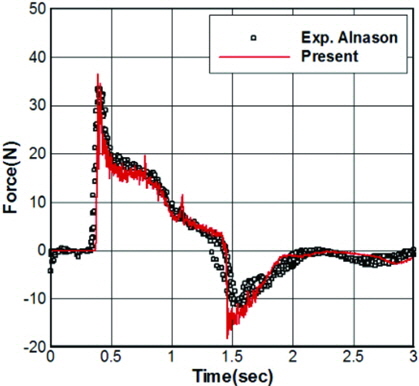
Fig. 3은 구조물의 전·후면에 작용하는 파력의 시간변화를 Radd and Bidoae(2005)의 실험과 비교하여 나타낸다. 그림에서, 양(+)의 힘(Positive force)은 유체가 구조물의 전면부에서 작용하는 힘을, 음(−)의 힘(Negative force)은 구조물 후면부에 작용하는 힘을 의미한다. 그리고, 실선으로 나타낸 수치모사의 결과는 최대 충격력이 나타나는 시각에 맞추어 위상차를 다소 보정하여 나타내었다. 한편, Fig. 4는 최대 파랑 충격이 나타나는 시각
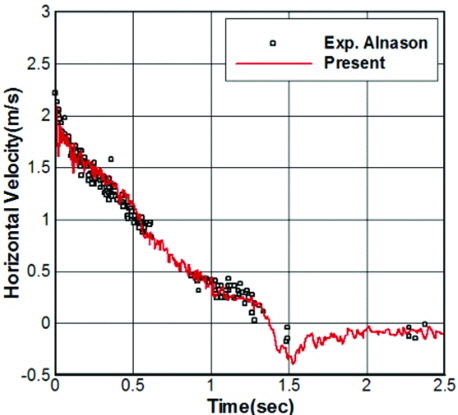
Fig. 5는 구조물의 전방 0.146(m), 바닥으로부터 0.026(m) 떨어진 지점에서 수평속도 성분의 시간변화를 실험과 비교하여 나타낸다. 실험에서는 LDV(Laser doppler velocimeter)로 속도를 측정하였으며, 수치모사에서는 지정 위치에서 미소 영역내에 포함되는 입자들의 평균속도를 측정하였다. 초기의 속도 분포에는 약간의 차이가 보이지만, 전체적으로 시간변화에 따른 속도의 감소 비율이 실험결과와 잘 일치한다.
상술한 바와 같이, 본 연구에서 적용한 입자법은 복잡한 자유표면의 비선형성 거동과 구조물과의 상호작용을 모사하기에 충분하며, 다양한 연안 구조물에 작용하는 파랑 충격력의 예측을 포함한 설계분야에 활용이 가능할 것으로 기대된다.
본 시뮬레이션은 Intel(R) Core(TM) I7 CPU 860 @2.8GHz, 4.0GB Memory의 PC에서 수행되었으며 총 CPU 시간은 24,682.64초가 소요되었다.
3.2 부가구조물 설치로 인한 연안구조물에 작용하는 파랑 충격력의 완화 효과
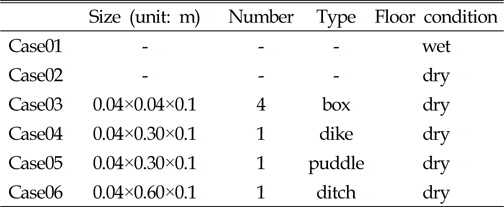
본 절에서는 높은 해안 구조물 전면에 낮은 소형 건물이나 수영장, 나무와 같은 장애물 혹은 하천 등의 유무에 따른 간섭효과를 고려하기 위해 Radd and Bidoae(2005)와 Radd의 연구진이 수행한 수치모사(University of Washington, 2005)와 유사한 5가지 형태의 부가구조물(Obstacle)을 설치하여 파랑 하중 완화 효과에 대해 수치적으로 모사해 보았다. Fig. 1의 점선으로 표시한 바와 같이, 부가구조물은 연안구조물(이후, 주 구조물)의 전면으로부터 0.04(m) 떨어진 지점에 설치하였다. 각 부가구조물의 설치 개수, 형상 및 크기를 Table 1에 정리하였다. 비교를 위해 3.1절에서 수행한 시뮬레이션을 Case01으로 하고, 나머지의 모든 경우는 수조 바닥의 물을 제거한 상태에서 계산을 수행하였으며, Case03의 경우의 부가구조물 간 간격은 0.04(m)로 설정하였다.
[Table 1] Dimension of obstacles
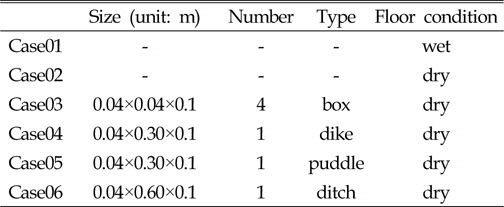
Dimension of obstacles
Fig. 6은 총 6가지 경우에 있어서 시간에 따른 자유표면 거동을 나타낸다. 수조바닥의 상태와 부가구조물의 형상에 따라 유동장의 상대적인 차이를 볼 수 있으나, 전체적인 경향은 전절에서 설명한 바와 유사하다.
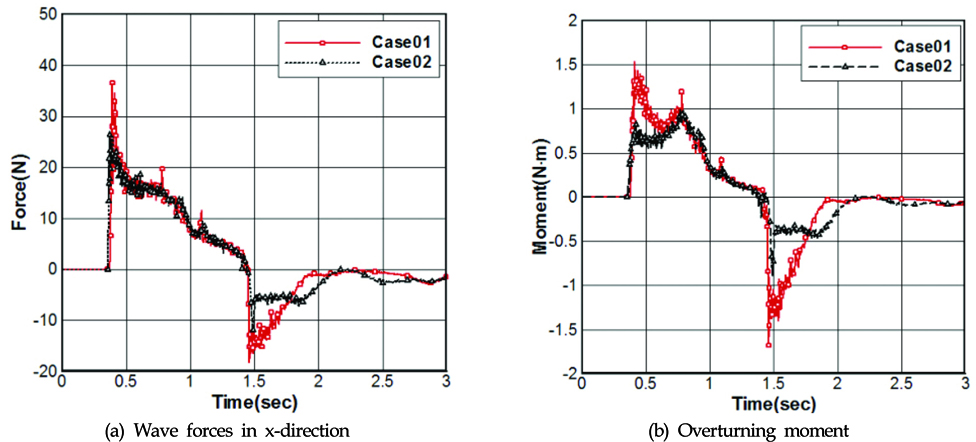
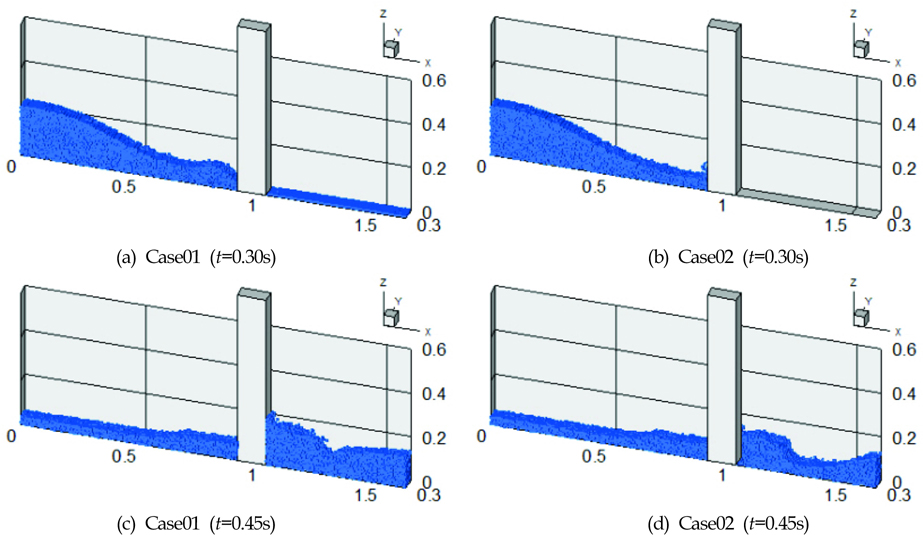
Fig. 7에는 Case01과 Case02의 경우에 있어서 주 구조물에 작용하는 파력과 회전 모멘트의 시계열 비교를 나타낸다. 수조의 바닥에 물이 차 있는 Case01은 그렇지 않은 Case02에 비해 상대적으로 주 구조물에 충격력(Impact force)으로 작용하는 유량(Flow)이 더 많기 때문에 주 구조물 전체에 걸리는 파력이 더 크게 나타난다. 한편, 주 구조물에 작용하는 회전 모멘트의 경우, 전체적인 경향은 뚜렷한 차이를 보이고 있는데, 이는 Fig. 8에서 보는 바와 같이 Case01의 경우 주 구조물에 작용하는 파의 최대 파고가 Case02에 비해 전면 약 50% 후면 약 30%가량 크기 때문에 모멘트 팔(Moment arm)의 길이가 길어져 상대적으로 큰 회전 모멘트가 작용하는 것으로 분석된다.
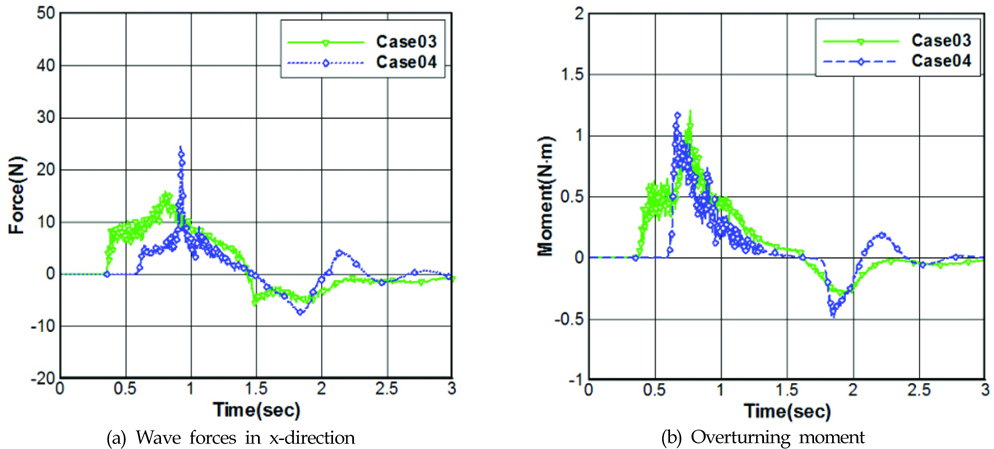
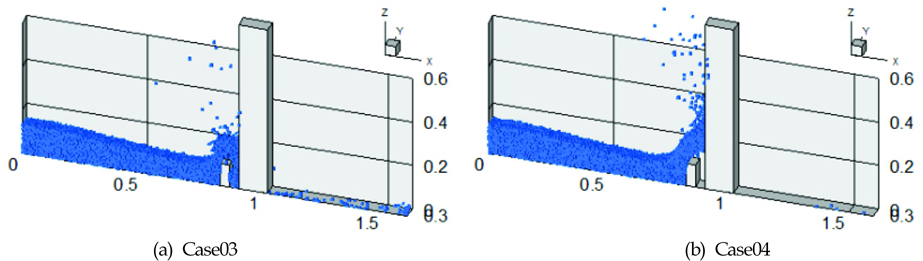
Case03과 Case04의 경우에 대하여, Fig. 9는 주 구조물에 작용하는 파력과 회전 모멘트를, 그리고 Fig. 10은 시각
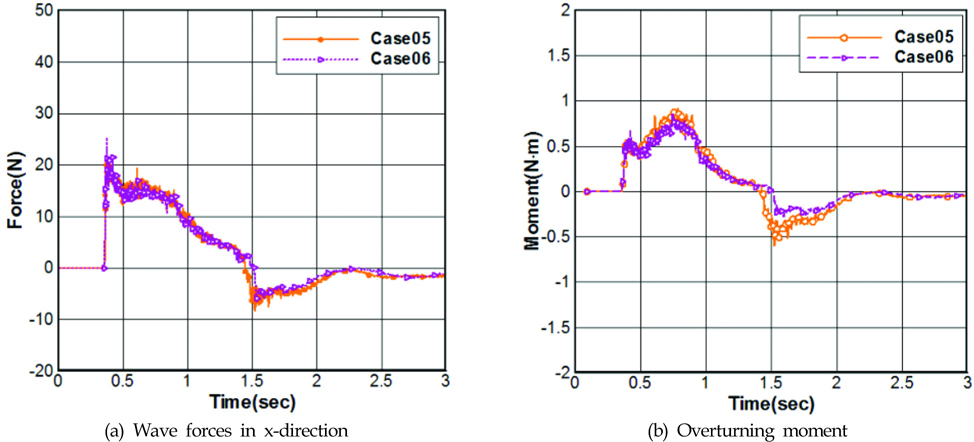
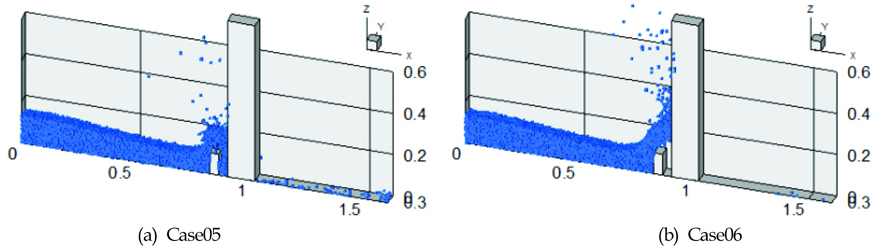
한편, Case05와 Case06의 경우에 대해 주 구조물에 작용하는 파력과 회전 모멘트를 Fig. 11에 나타내었다. 주 구조물에 작용하는 파력과 회전 모멘트에 대한 시간에 따른 변화는 Case02의 결과와 전체적으로 경향이 비슷하다. Case06의 경우 Case05에 비하여 주 구조물 전면의 웅덩이(Puddle)의 부피가 상대적으로 크기 때문에 상대적으로 많은 유량이 이를 메우는데 사용된다. 따라서 Fig. 12에서 보는 것과 같이 주 구조물에 작용하는 유량의 감소로 인해 파력이 감소된 것을 알 수 있다. 결과적으로 Case06의 파력과 회전모멘트의 변화는 Case05에 비해 상대적으로 덜 작아지게 된다.
마지막으로, 다양한 부가구조물 설치에 따른 파랑 하중 완화효과를 상대적으로 비교하기 위하여, 주 구조물에 작용하는 최대 충격력과 회전 모멘트, 그리고 시간 적분된 충격량(Time integrated impulse)과 회전 충격량(Time integrated angular impulse)을 산출하였다. Paik et al.(2004)은 구조물에 작용하는 충격하중을 고려한 구조물의 신뢰성 구조 설계를 위해서는 최대 충격력뿐만이 아니라 시간에 따른 하중의 변화 또한 중요한 해석변수임을 강조하였다. 시간에 따른 하중의 변화를 고려한 비교를 위하여 다음 식을 통해 충격량과 회전 충격량을 계산하고, 다양한 부가구조물의 설치에 의한 파랑 하중 완화 효과를 비교해보았다.
단, 위 식의
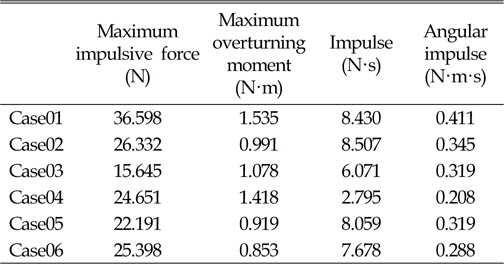
Table 2는 산출된 유체력을 비교 정리한 표이다. 단순히 주구조물만 설치된 경우에 비하여 부가구조물 설치로 인한 유체력이 감소되었을 알 수 있다. 이를 이용하여, Table 2와 같은 특정 수치를 이용한 평가뿐 아니라 유동장의 거동에 대한 해석을 통한 구조물 설치 환경 및 용도에 대한 다양한 부가물의 특성 파악 및 설계에 활용될 것으로 기대된다.
[Table 2] Comparison of hydrodynamic forces and moments acting on a tall structure
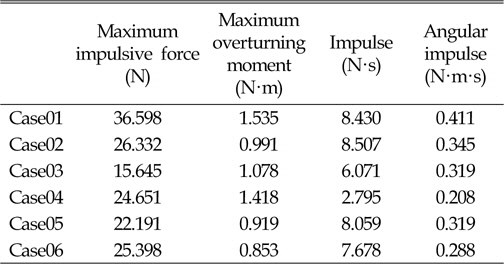
Comparison of hydrodynamic forces and moments acting on a tall structure
본 논문에서는 Koshizuka and Oka(1996)가 제안한 MPS법을 개량한 PNU-MPS법(Lee et al., 2011)을 기본으로 국소지역에서 지진해일과 같은 너울성 단일 대형 파랑이 연안구조물에 작용하는 유동장을 수치모사하고, 구조물에 작용하는 파력과 전진속도의 시간변화를 Radd and Bidoae(2005)의 실험 결과와 비교하여 잘 일치함을 보였다. 또한 연안구조물 전면에 다양한 부가구조물을 설치하여 이에 따른 파랑 충격 완화 효과에 대해서 수치모사하고, 완화 효과에 따른 유체력에 대하여 비교․분석하였다. 최대 충격 하중을 완화시키기에는 사이 틈새를 갖는 상자형의 부가구조물이 가장 효과적이었다. 향후 지진해일이 연안에 도달해서 붕괴될 때를 가정하여 연안구조물의 설계 시 대형 파랑에 의한 집중 하중의 완화를 위한 다양한 부가구조물의 형상개발 및 설치와 관련된 실질적인 적용기술의 개발이 가능할 것으로 보인다.