The exploration areas for maritime resources such as oil and natural gas have gradually moved to deep sea areas. It has become difficult to use existing fixed marine structures, which are very costly to build, because that have reached the uppermost economic limit. Therefore, floating marine structures and flexible marine structures are preferred. In particular, slender bodies such as risers and pipes are important parts of ocean depth marine structures. These slender bodies have more flexible structural characteristics in deep water areas because their overall length becomes longer and thediameter/length slenderness ratio gets smaller. In addition, the dynamic behavior of slender bodies becomes complicated as external forces such as tides and waves act on it directly. In this study, in order to solve these problems, we performed model tests in a 2-D wave basin using flexible slender bodies with different modulus of elasticity values. As a result, we compiled statistics and compared the behaviors of flexible slender bodies with respect to the effect of the modulus of elasticity. We expect that the results could be used as reference data for the design of structures with flexible elements.
해저 탐사 기술, 부유체 설계 기술, 그리고 심해 석유/천연가스 생산 기술의 발달에 따라 해저자원 개발 대상 해역은 점차 수심이 깊은 곳으로 이동하게 되었다. 탐사영역이 심해 영역으로 이동하면서 기존의 고정식 해양구조물은 건조비용의 상승과 안전성의 문제로 사용되기가 어려워지고 있으며 상대적으로 부유식 해양구조물이나 유연식 해양구조물들이 선호되고 있는 실정이다. 특히, 이러한 심해용 자원개발 해양플랜트에 있어서는 부유체와 Subsea system을 연결하는 라이저(Riser), 위치유지를 위한 계류삭(Mooring lines), Subsea system을 이루는 파이프(Pipe) 등과 같은 세장체 요소들이 해양플랜트의 구성에 있어 중요한 부분을 차지한다.
해양구조물을 이루는 세장체는 수심이 깊은 영역으로 갈수록 전체 길이가 매우 길어지고 상대적으로 직경/길이의 세장비가 커지게 되어 점점 더 유연한 구조물의 특성을 지니게 되고 있다. 세장체 구조물은 상부 구조물의 운동에 의해 야기된 가진력과 조류와 파랑과 같은 직접적인 외력을 받게 된다. 또한 조류와 파랑과 같이 흐름 방향(in-line)으로 작용하는 힘 외에도 이에 부차적인 와동방출(Vortex shedding)이 발생하게 된다. 이로 인하여 세장체 해양구조물의 동역학적 거동이 더욱 복잡해지고, 해양구조물 시스템 전체 거동에 미치는 영향도 역시 증가하게 된다(Chucheepsakkul et al., 1995, Huang, 1992). 결국 심해역에 투입되는 세장체 해양구조물에 관한 동역학적 해석과 아울러 관련연구의 중요도가 높아지고 있는 추세이다(Burke, 1974).
세장체 해양구조물의 동력학적 특성에 대한 모형시험은 현존하는 시험설비 대부분이 가지고 있는 물리적인 한계로 인하여 기하학적, 동역학적 상사관계를 모두 만족시키는 것이 거의 불가능하여 다양한 방법의 근사적인 모형시험 기법이 연구 개발되고 있다(Hong et al., 2002).
석유자원 탐사 및 개발, 해양온도차 에너지 발전, 심해 천연 광물자원 개발 등에 사용되는 라이저나 파이프는 재질이 여러겹으로 겹쳐져 있는 철제관 등으로 되어있다. 그러나 해양심층수를 취수하기 위한 취수관 등은 가볍고 유연한 폴리에틸렌과 같은 재질을 사용한다. 따라서 세장체 해양구조물의 최적 설계를 위한 방안으로 재질에 따른 유연한 세장체 해양구조물의 거동에 대한 해석이 필요하다(Chena et al., 2009).
본 연구에서는 유연한 세장체 해양구조물의 거동을 모형실험을 통하여 관찰하고 그 결과를 해석하였다. 실험은 2차원 조파수조와 예인전차를 이용하여 탄성계수가 다른 아크릴, 폴리프로필렌, 테프론 3개의 소재로 만들어진 실험모형으로 실험을 실시하였다. 각각의 실험모형에 대해 여러 경우의 주기와 파고를 가지는 정현파(Regular wave)를 가하여 그 거동을 관찰하였다. 이때 거동을 관찰하기 위해서는 비디오레코더를 이용하여 기록된 영상을 사용하여 거동을 계측하고 그 결과를 비교 및 분석하였다. 그 결과, 부유체에 파를 주거나 모형과 파의 상대적인 위치에 변화가 있을 경우, 유체입자의 모형의 움직임과의 상대적 운동관계에 의하여 부유체의 거동에 많은 영향을 주는 것으로 확인되었다.
2.1.1 2차원 조파수조
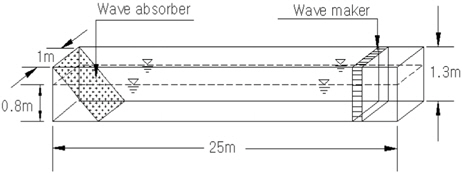
실험에서 사용된 수조는 Fig. 1에 나타낸 바와 같이 1×1.3×25m(B×D×L)의 조파수조로 조파기는 피스톤 형식이다. 수심 0.8m일 때 파고 0.3m까지 발생 가능하며, 파주기는 0.5~3.0s까지 가능하다. 본 수조에는 양방향 조류발생장치도 겸비하고 있으나 금번 실험에서는 조류중의 실험은 포함되지 않아 사용하지 않았다. 반사파의 영향을 최소화하기 위한 소파장치로는 하부에는 스펀지를 두고 상부에는 그물이 장착된 형태가 사용되고 있다.
2.1.2 예인 전차
실험에 사용된 예인전차는 Fig. 3와 같이 원통형 실린더를 예인하기 위한 장비로서 종방향(X방향), 횡방향(Y방향), 상하방향(Z방향), Rolling(
주행 레일(Running rail)은 정밀 주행이 가능하도록 크롬 도금이 되어있고, 수평도, 고저도 및 평행도를 조정할 수 있도록 되어있다. 또한 예인전차 주행 시험 시 모형에 의해 발생되는 부력 등에 의해 전차가 부상할 가능성을 방지하기 위해 LM shaft 시스템이 주행 레일에 사용되고 있다.
2.1.3 용량식 파고계
실험에서 사용된 용량식 파고계는 한 쌍의 평행한 와이어에서 물의 저항을 측정하여 DC전압으로 출력하는 저항식 파고계이다. 파고에 따른 비례적인 출력전압을 증폭하여 Span, Zero등으로 만족하는 출력을 얻고 신호를 외부계측기로 보내게 된다.
2.1.4 Video Recorder System
모델의 거동을 계측하기 위해 고화질 비디오레코더를 사용하였으며, 그 사양은 Table 1에 나타내었다.
[Table 1] Specification of camera

Specification of camera
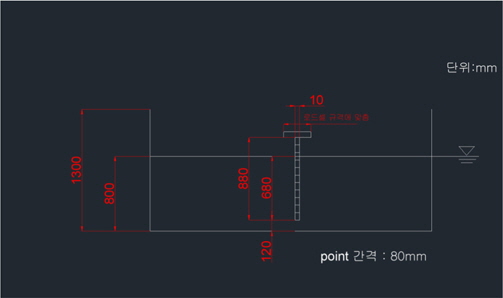
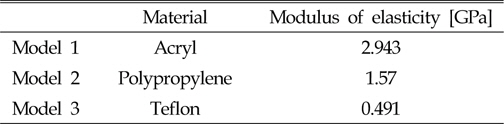
세장체의 거동을 관찰하기 위해 Fig. 4과 같이 상부는 얇은 원반형이며 아래부분에 세장체의 형상이 부착된 형태의 모델을 제작하여 사용하였다. 세장체의 지름은 1cm이며 제일 밑 부분으로부터 8cm 간격으로 표시를 해두어 그 부분의 거동을 계측한다. 모델은 Fig. 5과 같이 2차원 수조에 장착하였다. 세장체의 탄성치의 차이에 따른 거동을 관찰하는 것이 본 연구의 목적이므로 Table 2에 나타낸 바와 같이 아크릴(Acryl), 프로필렌(Polypropylene), 테플론(Teflon) 세가지 탄성계수를 지니는 소재로 모델들을 제작하였다.
[Table 2] Modulus of elasticity of models
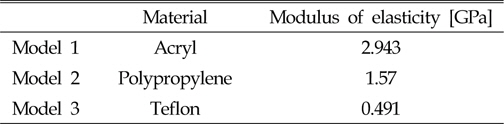
Modulus of elasticity of models
2차원 조파수조에서 탄성계수가 각각 다른 지름이 1cm인 세장체 모형을 가지고 실험을 실행하였다. 교정기(가로, 세로 각각 1m)를 사용하여 카메라에 찍힌 영상과 실험모델에 대한 교정작업을 수행하였다. 교정작업의 정도를 향상시키기 위해 교정기를 중앙을 중심으로 가로, 세로로10mm 간격으로 이동하면서 계측하였다. 이렇게 얻어진 영상으로부터 실측거리의 정보를 구하였다. 실험 데이터 계측의 정도를 높이기 위해 예인전차를 교정과정을 실시하여 주행시 진동을 최소화하고, 앞서 언급한 스폰지와 그물로 만들어진 소파장치를 이용해 반사파를 최소화 하였다.
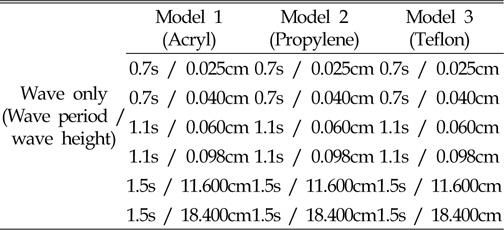
아크릴, 폴리프로필렌, 테플론의 다른 재질로 제작된 모형들을 Fig. 6와 같이 예인전차에 연결한다. 이 때 모형은 파랑의 이동방향과 평행한 방향으로 왕복운동이 가능하도록 전차에 장착하여 실험을 수행하였다. 실험은 크게 세가지 상황하에 수행되었는데, 첫째는 규칙파만 작용하고 모델은 고정된 경우, 둘째는 파도는 없이 모델만 단순 왕복운동하는 경우, 세번째는 규칙파가 작용하고 모델도 단순 왕복운동하는 경우이다. Table 3-Table 5은 실험조건들을 나타낸 표들이다. Table 3과 같이 규칙파만 작용하는 경우는 아크릴, 폴리프로필렌, 테플론 모두 실험이 수행되었으나, Table 4과 Table 5의 두가지 상황은 아크릴과 테플론 모델만 실험을 수행하였다. 실험의 재현성을 위하여 각 상황별로 5번씩 실시하였다. 각 상황 및 모델의 조합별로 계측되는 값들은 수조에서 계측가능한 시간내에 계측된 최대값을 기록하여 해석에 사용한다. Fig. 7는 실제 촬영장비를 통해 찍힌 실험의 한 장면이다.
[Table 3] Test conditions for wave only case
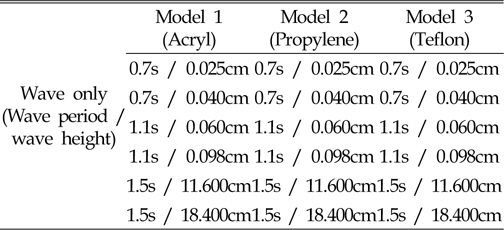
Test conditions for wave only case
[Table 4] Test conditions for motion only case

Test conditions for motion only case
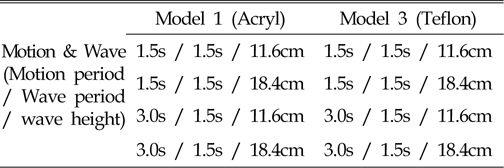
[Table 5] Test conditions for motion & wave case
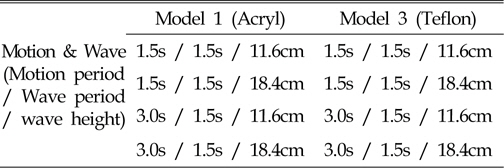
Test conditions for motion & wave case
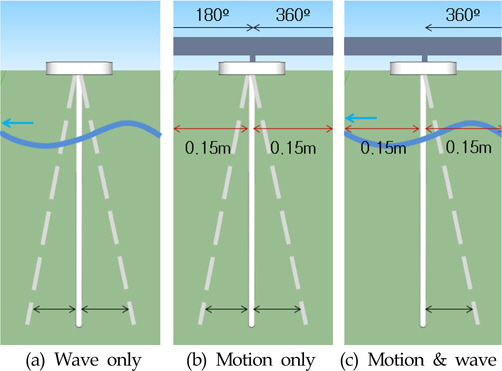
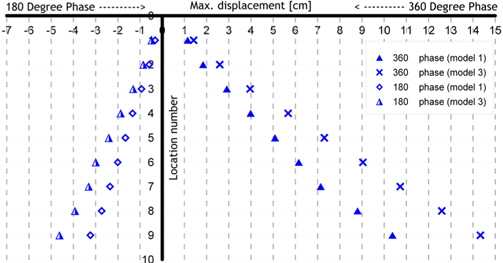
앞서 이야기 한 바와 같이 모형시험은 세 가지 상황 하에서 이루어지기 때문에, 각 상황마다 거동의 특성을 대표할수 있는 계측값을 정의하여 추출할 필요가 있다. 각 경우에 대한 계측량을 Fig. 8에 나타내었다. 첫번째, 모형은 고정되고 규칙파만 작용하는 경우(Fig. 8(a)), 모형의 중심을 기준으로 볼때, 파랑이 접근하는 방향(Upstream)으로의 최대변위와 파랑이 멀어지는 방향(Downstream)으로의 최대변위를 기록한다. 두번째, 모형은 0.15m의 진폭으로 왕복운동을 하고 파랑은 없는 경우(Fig. 8(b)), 모형의 중심이 시작점에 위치했을 때의 거동을 기록하되 모형중심의 위치가 시작위치와 180도의 위상을 가질때와 360도의 위상을 가질때의 최대변위를 구분하여 기록한다. 세번째, 모형은 0.15m의 진폭으로 Sinusoidal 거동을 하고 규칙파가 작용하는 경우(Fig. 8(c)), 360도의 위상을 가지는 시점에서의 최대변위를 기록하되, 모형이 왕복운동중에 파랑의 파정과 만났을 때와 파저와 만났을 때로 나누어 변위를 측정하였다. 이는 모델의 운동방향이 파랑의 진행방향과 같거나 역방향으로 움직일 때를 구분하기 위해서이다.
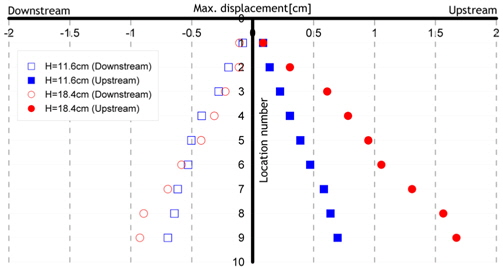
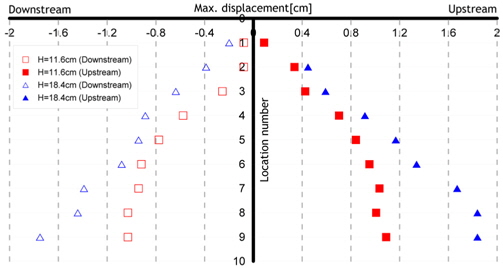
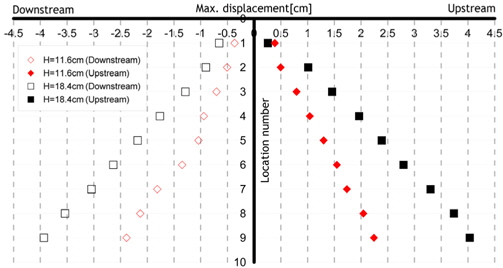
Fig. 9-Fig. 11는 각각 Model 1(Acryl), Model 2(Polypropylene), Model 3(Teflon)이 파주기 1.5s 일 때, 두 가지 파고인 11.6cm, 18.4cm에 대한 수심에 따른 모형의 변위를 나타낸 그림이다. Fig. 9의 경우, Upstream과 Downstream의 경우 비대칭성이 나타나 있는데, 이는 모델의 탄성으로 인한 거동과 파입자의 운동이 연성되어 나타나는 결과이다. 이러한 경향은 Fig. 12에서 촬영된 사진에서도 나타나 있는데, Upstream인 경우는 파저가 모델을 지나가는 순간 기록된 변위이고, Downstream인 경우는 반대로 파정이 모델을 지나가는 순간이 기록되어 있기 때문이다. 모델의 탄성으로 인한 좌우방향의 복원력은 좌우 대칭이지만, 파입자의 운동이 모델에 미치는 영향은 모델의 중앙에 파정이 위치하느냐, 또는 파저가 위치하느냐에 따라 다를것이기 때문에 좌우 비대칭성이 나타나는것으로 생각된다. Fig. 11에 나타난 결과는 Fig. 9의 결과에 비해 비대칭성이 적음을 알 수 있는데, 이는 Fig. 9에서 사용된 acryl의 탄성계수가 Fig. 11에서 사용된 teflon의 탄성계수보다 커서 acryl의 변형에 대한 복원성이 보다 teflon보다 커서 복원성과 파입자 운동의 영향의 연성효과가 보다 크게 나타나기 때문이다. Fig. 12은 각 모델들의 거동결과를 비교함으로써 모델 탄성계수가 거동에 미치는 영향을 정량적으로 비교하여 나타내었다.
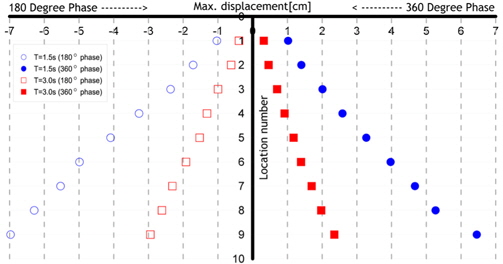
Fig. 13-Fig. 15은 Model에 Motion만 가했을 경우, 두가지 운동주기(1.5s와 3.0s)에 대한 각각 Model 1, Model 2, Model 3의 최대변위를 나타낸 그림이다. Fig. 13을 모델은 고정되고 파랑만 작용하는 Fig. 9과 비교해보면 Fig. 13에서 좌우방향을 의미하는 180deg.와 360deg.에서 보다 많은 좌우 대칭성을 띠고 있음을 관찰할 수 있다. 이는 Fig. 13에서는 Fig. 9에서 변위의 비대칭성을 일으키는 파입자의 영향이 없어졌기 때문이다. 이러한 경향은 Model 3(Teflon)에 대한 결과인 Fig. 14에서도 마찬가지로 나타나, 최대변위가 좌우대칭임을 알 수 있다. Fig. 15은 모델의 운동주기가 1.5s 일 때 Model 1과 Model 3의 탄성 변화에 따른 최대변위를 비교하여 탄성계수의 차이와는 무관하게 최대변위가 좌우 대칭성을 나타내고 있음을 보여주고 있다.
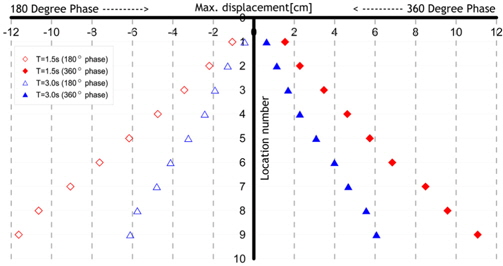
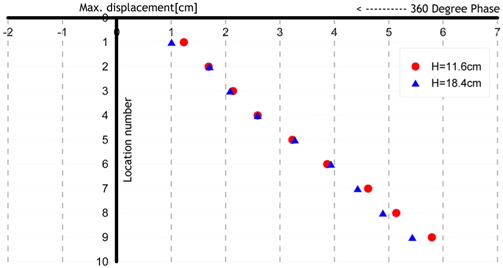
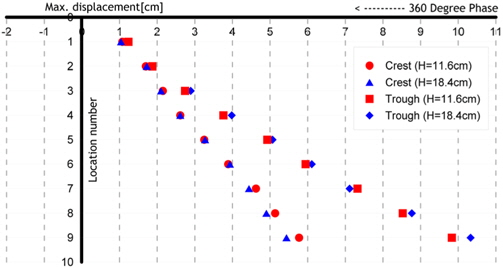
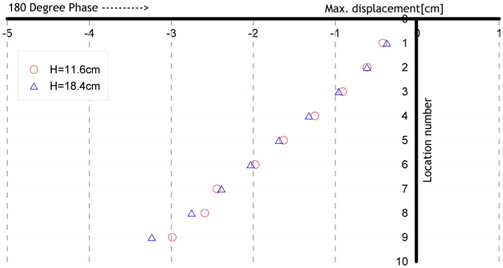
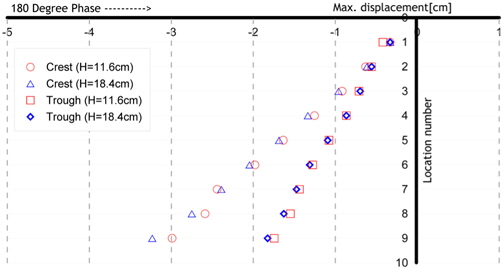
Fig. 16는 Model 1(Acryl)의 운동주기는 1.5s, 파랑주기는 1.5s, 계측된 시점은 모델운동의 위상이 360deg.일때, 모형이 파정과 만나는 경우, 두가지 파고(11.6cm, 18.4cm)에 따른 변위를 나타낸 그림이다. 파고의 변화에 비해 모델의 변위가 큰 변화가 없음을 관찰할 수 있는데, 이는 모델의 큰 탄성계수로 인해 파랑의 영향보다 탄성거동이 지배적이기 때문이다. Fig. 17은 Fig. 16의 결과에다 다른 조건은 모두 같고, 파도가 모형의 파저에 만나는 경우에 추가해서 비교한 결과이다. 마찬가지로 파저에 모델이 위치하는 경우도 파고의 변화에 대해 상대적으로 변위차이가 크지 않음을 알 수 있다. 파정과 파저에서의 결과를 비교해보면, 모델이 파저에서 만나는 경우가 파정에서 만나는 경우보다 큰 변위를 나타냄을 알 수 있다. 이는 3.1절에서 파랑만 존재하는 경우에서 관찰한 바와 같이 모델의 탄성에 기인한 복원성과 파입자 운동의 영향이 연성되어 나타나는 결과이다.
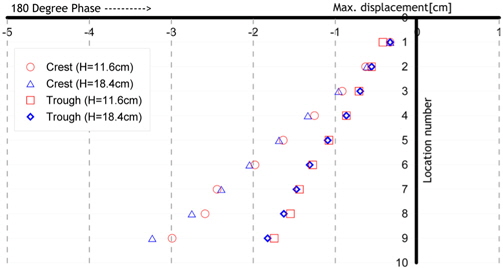
Fig. 18은 Model 3(Teflon)의 운동주기는 1.5s, 파랑주기는 1.5s, 계측된 시점은 모델운동의 위상이 360deg.일때, 모형이 파정과 만나는 경우, 두가지 파고(11.6cm, 18.4cm)에 따른 변위를 나타낸 그림이다. 같은 조건의 Model 1(Acryl)에 대한 실험결과인 Fig. 16와 달리 파고에 변화에 따른 모델의 변위가 크게 관찰되었다. 이는 Teflon의 탄성계수가 작기 때문에 모델의 탄성복원력이 작아서 파랑에 의한 영향이 보다 크기 때문이다. Fig. 19는 Fig. 18의 결과에 모델이 파저와 만나는 경우를 추가한 그림이다. Model 1 (Acryl)에 대한 결과인 Fig. 17과 마찬가지로 모델이 파저에 위치하는 경우가 파정에 위치하는 경우보다 큰 변위를 관찰할 수 있다. 파저에 위치한 경우는 운동방향과 파랑입자의 운동방향의 상쇄작용으로 파고의 변화가 크게 나타나지 않기 때문으로 생각된다.
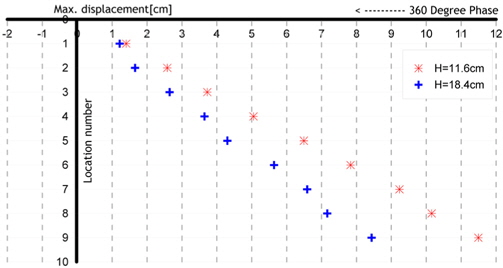
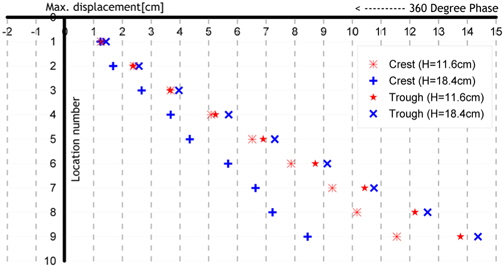
Fig. 20는 Model 1(Acryl)의 운동주기는 1.5s, 파랑주기는 1.5s, 계측된 시점은 모델운동의 위상이 180deg.일때, 모형이 파정과 만나는 경우, 두가지 파고(11.6cm, 18.4cm)에 따른 변위를 나타낸 그림이다. 다른 조건들은 동일하나 계측지점의 위상만 360deg.인 Fig. 16의 결과와 비교해 볼 때, 마찬가지로 모델의 탄성계수가 크기 때문에 파고의 변화가 모델의 변위에 큰 영향을 미치지 않음을 볼 수 있다. Fig. 21는 Fig. 20의 결과에 파저에서 관측한 결과를 추가한 그림으로, 파저에 모델이 위치하는 경우도 파고의 변화에 대해 상대적으로 변위차이가 크지 않음을 관찰할 수 있다. Fig. 17과 비교해보면, 파정과 파저에서의 변위의 크기가 반대로 파정에서 크게 나타남을 알 수 있는데, 이는 파저에 모델이 위치했을 때 모델의 운동방향과 파랑입자의 운동방향이 서로 상쇄되는 방향으로 움직이기 때문으로 생각된다.
Fig. 22는 Model 3(Teflon)의 운동주기는 1.5s, 파랑주기는 1.5s, 계측된 시점은 모델운동의 위상이 180deg.일때, 모형이 파정과 만나는 경우, 두가지 파고(11.6cm, 18.4cm)에 따른 변위를 나타낸 그림이다. 같은 조건에서 모델의 위상이 360deg.의 결과인 Fig. 18의 결과와 비교해보면 파고에 대한 변위의 변화가 크지 않음을 관찰할 수 있는데, 이는 모델의 운동방향과 파입자의 운동이 서로 상쇄된 결과로 생각된다. Fig. 23은 Fig. 22의 결과에 모델이 파저와 만나는 경우를 추가한 그림이다. 눈에 띄는 결과는 모델이 파저에 위치했을 때 전체적인 변위가 작게 나타났다는 것이며, 파저에 위치한 경우에는 운동방향과 파랑입자의 운동방향의 상대적인 방향이 변위가 커지는 방향으로 작용하기 때문이다.
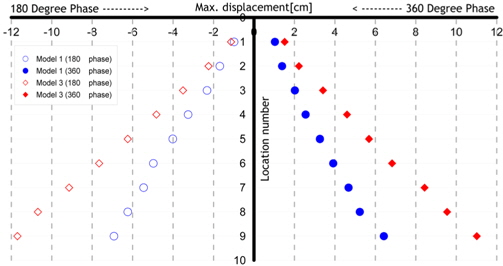
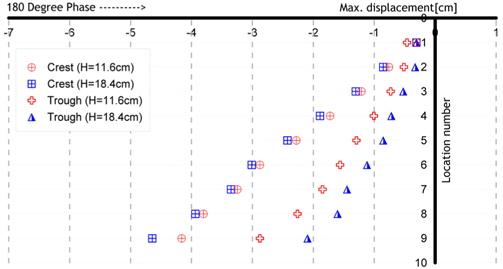
이상의 결과를 종합하는 대표적인 경우중 한가지를 Fig. 24에 나타내었는데, Acryl과 Teflon의 모델이 파저에 위치했을때, 180deg.의 위상과 360deg.의 위상을 가지는 경우 모델의 변위를 표시하였다. 모델이 파정에 위치하는 경우는 그림과 같이 360deg.의 위상을 가질 때 전체적으로 큰 변위를 나타내었으며, 탄성계수가 더 작은 Teflon의 경우가 탄성계수가 큰 Acryl보다 큰 변위값을 나타내고 있어 Teflon의 경우 탄성계수값이 작기 때문에 탄성복원력보다 파랑입자에 의한 영향이 더 크다는 것을 보여주고 있다.
본 논문에서는 심해용 해양플랜트의 구성요소들이 지니는 세장체의 거동에 대한 기초적 연구로써, 각기 다른 탄성계수를 지니는 소재로 세장체 모형을 제작하여 2차원 수조에서 다양한 조건에서 세장체의 거동을 계측하였다. 그 조건들은 모델의 운동과 파랑의 조합, 작용하는 파랑의 파고, 모델의 변위를 계측하는 위상과 위치를 포함한다. 모형실험을 통한 계측결과로부터 다음과 같은 결론을 얻을 수 있었다.
(1) 모형의 운동만에 의한 세장체의 변위는 좌우 대칭인 반면, 파 또는 파와 모형의 운동을 동시에 고려하였을 경우에는 비대칭인 경향을 보인다. 이 때, 파정보다 파저가 모형과 같은 위치에 있을 때, 모델의 변위가 크게 나타났다.
(2) 파와 모형의 운동이 동시에 작용하는 경우, 운동의 위상과 파정 또는 파저의 위치에 따라 최대변위가 영향을 받음을 실험을 통하여 확인하였다. 이는 모델의 운동방향과 파입자의 운동방향의 상대적인 방향에 의한 영향으로 설명이 가능하다.
(3) 본 실험은 2차원 수조에서 이루어져 2차원 변위만을 측정하였지만, 실험을 통해 3차원 운동이 발생하는 것을 관찰할 수 있었고, 이는 모델과 유체입자의 상대운동으로 인한 Vortex shedding현상으로 인한 것으로 생각된다. 이러한 현상들의 불확실성으로 인해 본 실험만으로는 세장체 운동변위에 대한 정량적인 평가에 무리가 따르기 때문에 향후 추가적인 실험과 통계적인 해석법을 도입할 경우, 보다 정량적인 결과도출이 가능할 것으로 생각된다.