In this paper, the effects of a foil attached to a ship on the ship motion, added resistance, and thrust generation in waves are analyzed. The unsteady theory for a two-dimensional foil is introduced to determine the coupled motion responses of the ship and foil. The thrust caused by the oscillating foil is evaluated and compared to the added resistance of the ship, so that a positive net thrust can be possible in waves. A comparison of the results of unsteady, quasi-steady, and experimental analyses is performed.
선박에 날개를 부착하여 파랑 중 선체운동을 감소시키거나 날개로부터 추력을 얻고자하는 연구가 수행되어 왔다. 이를 위해서는 동요하는 날개에 의한 양력 및 추력발생에 대한 연구와 날개에 의한 힘을 선체운동과 연성시켜 해석하는 연구가 필요하다. Bessho and Kyozuka(1984)는 준정적 2차원 날개 해석법을 사용하여 날개에 의한 선박의 동요저감과 부가저항의 감소에 대해 연구하였다. Nagahama et al.(1986)도 준정적 해석법을 사용하여 선박의 동요저감 및 날개에 의한 추력발생을 해석하였고 모형시험을 수행한 바 있다. 최근에 Choi(2012)는 비정상 2차원 날개이론에 근거하여 전파하는 수직변동유장 중 동요하며 전진하는 날개에 의한 양력과 추력을 해석하였다.
본 연구에서는 Choi(2012)의 비정상 날개해석법을 사용하여 날개운동과 선박운동의 연성방정식을 도출하고, 날개에 의한 선박운동의 영향을 고찰한다. 날개영향을 고려한 선박과 날개의 운동응답을 이용하여 선박에 작용하는 파랑 부가저항과 날개에서 발생하는 추력을 해석하여 파랑에너지로부터 부가저항보다 큰 추력을 획득할 수 있는지를 검토한다. 이와 더불어 준정적 해석법과 비정상 해석법의 결과를 비교검토한다.
파랑 중 선박은 파랑의 기진력으로 인해 6자유도 운동을 하게 된다. 본 연구에서는 Fig. 1과 같은 병진운동(
여기서
이러한 선박에 Fig. 2 와 같이 선박 좌표계 원점으로부터 선수방향으로 거리
날개에 작용하는 유체력 및 날개운동을 해석하기 위해 다음과 같은 가정을 도입한다.
날개는 조우원주파수로 조화운동을 하며 운동의 진폭은 작다.
날개의 두께는 길이에 비해 매우 작으며 상하 대칭인 형상이다.
파랑에 의한 유체속도는 선속, 즉 날개의 파랑 중 전진속도에 비해 크기가 매우 작다.
날개와 자유표면과의 상호작용은 무시한다. 파랑에 의한 수직 변동류의 크기는 날개가 잠긴 수심에서의 수직방향 유체속도를 이용한다.
날개 단면에 대해 2차원적 해석을 수행하며 날개폭(Span, s)의 효과는 날개폭에 수정계수를 곱하여 보정한다. 이때 날개단면에 대한 2차원적 해석은 선체중심선(Center line,
이상의 가정에 따라 날개의 평균 캠버선(Mean camber line)에 대하여 선형 포텐셜이론을 적용할 수 있다(Choi, 2012). 이때 평균 캠버선은 상하 대칭인 날개이므로 평판날개에 해당한다. 그리고 날개의 조화운동은 다음과 같이 표현된다.
여기서
Choi(2012)는 전파하는 수직변동 유장 중 전진하며 동요하는 날개에 대한 양력 및 추력을 해석하였는데 선형중첩원리에 의해 정수 중 전진하며 동요하는 평판날개문제와 전파하는 변동 유장 중 전진하는 고정된 평판날개문제로 분리하여 선형문제를 해석하였다.
여기서
먼저, 정수 중 동요하는 평판날개에 의한 양력과 모멘트는 식 (3)의 조화운동에 따라 다음과 같이 표현된다(Choi, 2012).
여기서 *는 공액복소수를 의미하고,
또한 식 (5)와 (7)에서 변위 위의 두 점 및 한 점은 각각 변위 방향의 가속도와 속도를 의미한다. 그리고
이들 식에서 사용된 는 2차원 물리량들을 3차원의 물리량들로 확장하기 위해 곱해진 유효 날개폭으로 다음과 같이 가정하였다(Nagahama et al., 1986).
여기서
전파하는 수직변동유장 중 전진하는 2차원 고정날개문제에서 입사각
파랑의 날개길이방향 전파속도와 날개의 전진속도간의 상대속도를 고려하여 Choi(2012)의 해석결과에 적용하면
여기서
여기서
이상의 날개에 의한 양력과 모멘트를 선박의 운동방정식과 연성시켜서 운동응답을 구할 수 있는데 날개의 상하운동(
본 연구에서는 상하동요와 종동요 그리고 날개의 회전운동을 서로 연성시켜 해석하였다.
여기서
날개에 의한 시간평균 추력()은 2차항의 힘으로 Choi(2012)의 연구결과를 사용하여 추정할 수 있다. 추력은 6개의 성분으로 표현되며 날개 회전운동, 날개 상하운동 그리고 수직 변동유속의 크기를 사용하여 2차전달함수로 표현된다(Choi, 2012). cos
여기서
식 (17)-(19)의 해와 식 (16)의 관계로부터
선박에 날개를 부착함으로써 파랑 중에 추가적인 추력을 얻기 위해서는 파랑에 의해 선박에 작용하는 부가저항을 고려하여야 한다. 이는 날개에 의한 추력으로 선박의 파랑 중 부가저항을 일정부분 상쇠하는 효과도 있지만, 파랑에너지를 이용한 추진시스템으로 이라는 능동적 관점에서는 부가저항 보다 큰 날개추력이 요구된다.
본 연구에서는 Gerritsma and Beukelman(1972)의 방법에 따라 선박에 작용하는 파랑부가저항(
여기서 적분은 선미로부터 선수방향으로의 적분이고
여기서
본 연구결과를 적용하기 위해 내항성 분야의 공시선형으로 알려진 ITTC S-175 컨테이너선을 채택하여 해석을 수행하였다. 이 선박의 수선간 길이(
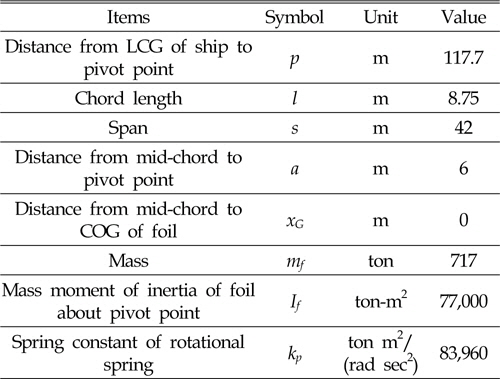
[Table 1] Principal particulars of foil
Principal particulars of foil
Table 1의 날개는 Nagahama et al.(1986)이 S-175선박에 부착하여 실험한 날개와 동일하며 본 연구의 해석결과와 비교하기 위해 채택되었다. 날개가 잠긴 수심은 17.24m이며, a값이 날개 길이의 절반보다 크므로 회전점이 날개의 앞전 전방에 위치한다(Fig. 2 참조). 본 연구결과에서 비교하는 실험결과는 모두 Nagahama et al.(1986)의 결과이다.
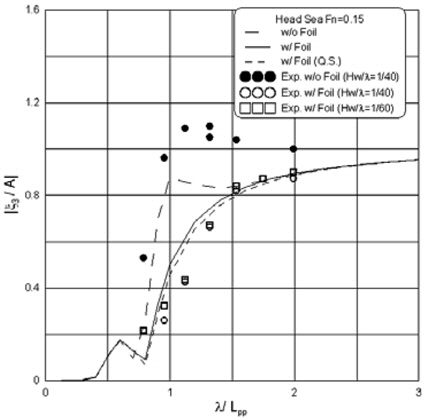
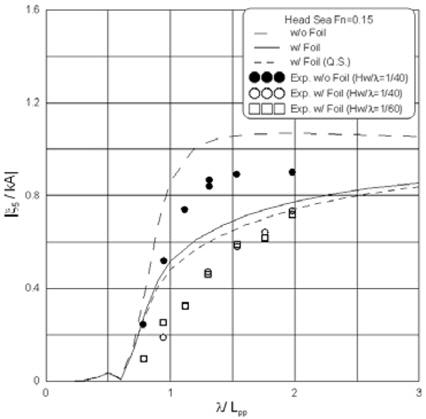
Fig. 3과 Fig. 4에 각각 입사파의 파진폭(
Fig. 5에 선수파 중 날개의 회전운동응답을 도시하였다. 실험 결과와 계산결과사이에 상당한 차이를 보이나 정성적인 경향은 유사하다. 선형물리량인 날개 회전운동 역시 준정적 해석과 비정상 해석간의 차이는 매우 적다.
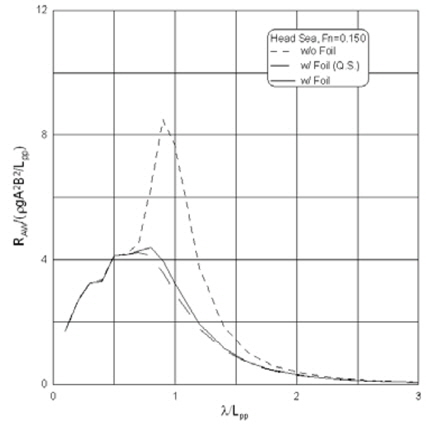
본 연구에서 도입한 Gerritsma and Beukelman(1972)의 부가저항 해석법의 유용성을 살펴보기 위해 날개가 없을 때의 부가저항 해석결과를 실험치와 비교하였다 (Fig. 6). 부가저항이 2차항의 힘임에도 불구하고 계산결과가 실험결과와 비교적 잘 일치하여 본 연구에서 사용한 부가저항해석법이 유용함을 알 수 있다.
Fig. 7에 날개를 부착하였을 때의 선수파 중 부가저항을 도시하였다. 날개부착에 의해 부가저항이 상당히 감소함을 알 수 있다. 이는 Fig. 3과 4에서 보듯이 날개에 의해 선박의 상하동요와 종동요가 감소하여 부가저항에 가장 큰 영향을 미치는 수직상대운동이 감소하였기 때문이다. 선박의 운동은 준정적 해석과 비정상 해석간의 차이가 거의 없으므로 부가저항 역시 차이가 매우 적다.
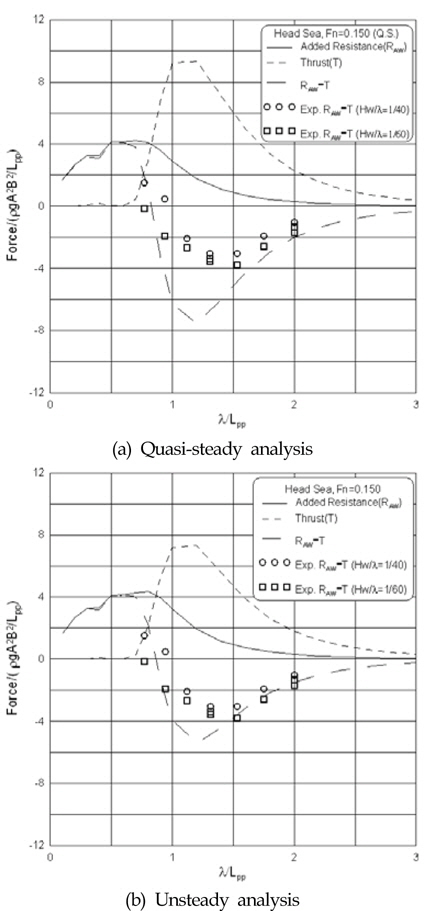
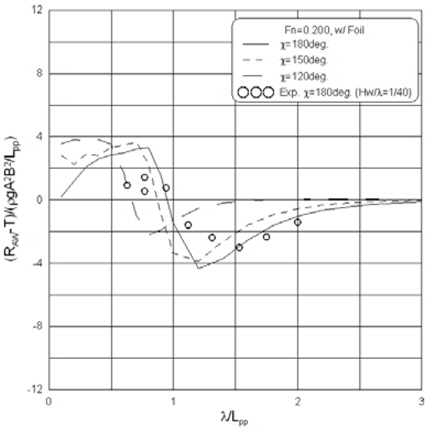
후루드수가 0.15이고 선수파 중인 경우에서 날개에 의한 추력(
후루드수가 0.2이고 선수파 및 선수사파 중인 경우, 순저항값의 비정상 해석 결과를 Fig. 9에 도시하였다. 선수파에서 횡파 방향으로 파랑 입사각도가 변하면 추력획득효과가 감소함을 알 수 있다.
본 연구에서는 파랑 중 선박에 부착된 동요하는 날개가 선박의 운동에 미치는 영향을 해석하였고, 날개에 의한 추력을 추정하였다. Choi(2012)의 연구결과를 토대로 파랑 중 동요하는 날개에 의한 양력 산출식을 선박의 운동방정식과 연성시켜 선박의 운동 응답과 날개의 운동을 해석하였다. 이를 토대로 날개에서 발생하는 추력을 추정하였고, 파랑 중 선박에 작용하는 파랑부가저항과 비교하여 파랑에너지로부터 순추력의 획득가능성을 검토하였다.
S-175선박에 특정 날개를 적용하여 해석해 본 결과 날개 부착에 의해 선박의 상하동요와 종동요가 감소하였고, 운동의 감소에 따라 부가저항도 감소하였다. 날개에 의한 추력과 선박에 작용하는 파랑부가저항의 비교를 통해 운동응답이 큰 파랑영역에서 순추력이 발생함을 확인하였다. 이러한 결과들은 실험치에서도 확인할 수 있었다. 준정적 해석법과 비정상 해석법 결과들을 비교해보면 선형운동응답 및 선박부가저항에서는 거의 동일한 결과를 보이는데 반하여 날개의 추력에서는 상당한 차이를 보이고 있으며 비정상 해석 결과가 실험치에 더 근접한 결과를 보였다. 따라서 추력해석을 위해서는 후류와도에 의한 시간기억효과를 엄밀히 고려하는 비정상 해석이 요구된다.
본 연구에서는 2차원 해석을 통한 날개효과를 3차원으로 확장하는데 있어 날개 종횡비를 이용한 약산식을 사용하였으나, 좀 더 엄밀한 해석을 위해서는 날개의 3차원효과를 고려한 양력 및 추력해석법이 필요하리라 생각되며, 날개와 자유표면의 상호작용도 연구할 필요가 있다. 또한 날개의 회전운동이 실험치와 큰 차이를 보이는 원인에 대해 심도있는 검토가 필요하리라 사료된다.