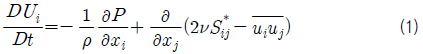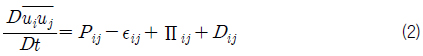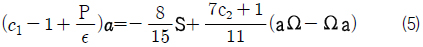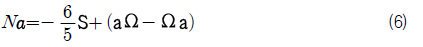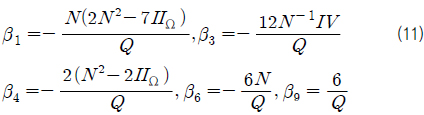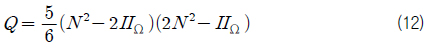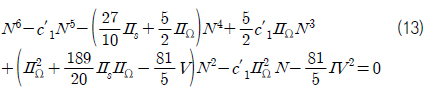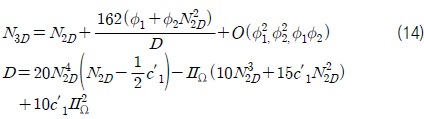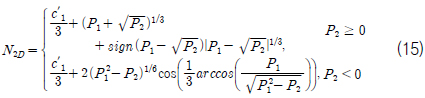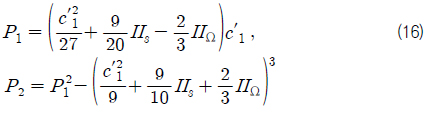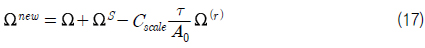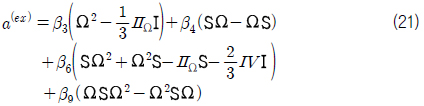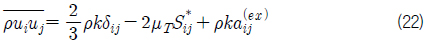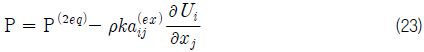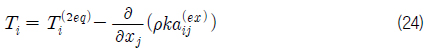In this study, Explicit Algebraic Reynolds Stress Model (EARSM) which is based on the existing 𝒌−𝛜 model has been applied to the flow field analysis around ship hulls. Existing transport equations for the turbulent kinetic energy and the dissipation rate are used in almost the same form and anisotropy terms of Reynolds stresses are newly considered. The well-known KVLCC2 and KCS hull forms are selected as validation cases, which were also used in 2010 Workshop on CFD in Ship Hydrodynamics. In case of KVLCC2 double model, comparison of mean velocity distribution, turbulent kinetic energy, and Reynolds stresses near the propeller plane has been carried out and wave elevation and wave profiles have been additionally studied for KCS and KVLCC2 with free surface models. Some improved results for mean velocity distribution at the propeller plane have been obtained while there is little change in free surface wave profiles.
공학적 유동 해석에 사용되는 RANS(reynolds averaged navier-stokes) 방정식 기반의 CFD 방법들의 대부분은 난류 모델 로서 2-방정식 모델(two-equation model)을 채용하고 있다. 이는 선박 유체 동역학적 성능 추정에도 마찬가지이다. 물론 DNS(direct numerical simulation)와 LES(large eddy simulation)등의 방법들이 소개되고 있지만, 공학적 응용 분야, 특히 선박 주위의 유동과 같은 고레이놀즈수 유동의 해석에서는 사용이 극히 제한적인 실정이다. 2-방정식 모델은 컴퓨팅 시간이 적고, 비교적 좋은 결과를 제공하기 때문에 많은 변형된 모델들이 제안되어 사용되고 있다. 하지만, 이러한 모델들은 몇 가지 단점들을 갖고있다. 예를 들어, streamline curvature 효과를 고려하는데 취약하고, 역압력 구배(adverse pressure gradient)에 대한 예측 능력이 떨어지며, 유동 박리를 잘 예측하지 못하는 점들이다. 이러한 단점들은 2-방정식 모델들이 Boussinesq 가설에 기반한 방법들이라는 사실에 기인한다. 앞서 예를 든 유동 현상은 선박의 후류에서 흔히 발생하는 현상으로, 2-방정식 모델이 선박의 후류 유동장 모사에 적합하지 않을 수 있다는 점을 의미하기도 한다. 이러한 이유로 2-방정식 모델을 대체하기 위하여 레이놀즈 응력 모델(reynolds stress model; RSM)이 제안되었다. 레이놀즈 응력모델에서는 Boussinesq 가설을 이용하지 않고 레이놀즈 응력을 수송방정식을 사용하여 계산한다. 하지만, 구현이 복잡하고 3차원 문제에서 해의 안정성이 확보되지 못하며 계산 시간도 많이 소요되는 단점을 갖고 있다. 반면, EARSM(explicit algebraic reynolds stress model)은 RSM으로부터 몇 가지 가정을 통해서 얻어지는데, 2-방정식 모델에 비해서 많은 유체 역학적 물리량을 포함하고 수치적으로도 매우 강건하며 2-방정식 모델과 비슷한 수준의 계산 시간을 필요로 하는 장점을 갖고 있다. EARSM은 Pope(1975)가 처음 제안한 이래로, Taulbee(1992), Gatski and Speziale(1993), Girimaji (1996), Johansson and Wallin (1996)등에 의해 계속 발전되어 왔다. 최근에 Wallin and Johansson (2000)이 3차원 문제에 이를 적용하였으며, 관련된 연구들이 계속 발표되고 있다. 선박 문제에 있어서는 Deng and Visonneau (1999)가 𝒌−𝛜 모델을 기반으로 한 EARSM을 HSVA tanker에 적용한 바 있으며, Yang, et al. (2010)은 RSM을 선박 문제에 적용하여 고차 난류모델의 필요성에 대해 밝힌 바 있다.
본 연구에서는, 선형 설계 현장에서 저항 및 자항 성능 평가기술로 비교적 높은 신뢰도를 얻고 있는 WAVIS2.2 (Kim, et al., 2011)를 바탕으로, 이에 사용되고 있는 𝒌−𝛜 2-방정식 모델을 기반으로 유도된 EARSM을 공개 선형인 KCS와 KVLCC2에 적용하여 검증을 수행하였다. 다음 장에서는 EARSM의 정식화를 보 이고, 이를 적용한 결과를 기존의 realizable 𝒌−𝛜 모델의 결과 및 실험 결과와 비교한다.
RANS 방정식은 Navier-Stokes 방정식에 평균을 취함으로써 얻어지며, 다음과 같은 형태를 갖는다.
여기서 평균 변형률 속도(mean strain rate) 텐서는 로 정의 된다. 식 (1)의 마지막 항인 레이놀즈 응력항은 2-방정식 모델의 경우 난류 점성 계수(turbulent viscosity; 𝑣
식 (2)의 우변 항들은 각각 생성(production), 소산(dissipation), 압력-스트레인 비율(pressure-strain rate), 확산(diffusion)을 의미한다. 생성항은 레이놀즈 응력의 함수로 직접 표현되며, 나머지 항들은 모델링이 필요하다. 레이놀즈 응력은 symmetric, traceless 행렬인 비등방성 레이놀즈 응력(Reynoldsstress anisotropy)으로도 표현될 수 있으며 다음과 같이 나타낼수 있다.
일반적으로 평균 속도 구배(mean velocity gradient) 텐서는 평균 변형률(mean strain)과 평균 회전(mean rotation) 텐서로 나누어 다루는 것이 편리하다.
소산항과 압력-스트레인 비율항에 몇몇 가정들과 모델링 기법을 적용하면 비등방성 레이놀즈 응력에 대한 음함수 형태의 대수 방정식(algebraic equation)을 식 (5)와 같이 얻을 수 있다. 자세한 유도 과정은 본 논문의 범위를 벗어나는 것으로 Wallin and Johansson (2000)의 논문에 기술되어 있다.
Rotta 상수
여기서
비등방성 레이놀즈 응력 텐서를 구하기 위한 가장 일반적인 형태는 Caley-Hamilton 정리를 이용하여 10개의 독립적인 텐서로 표현될 수 있다 (Pope, 1975).
식 (6)을 풀기 위한 과정을 정리하면 다음과 같다.1) 식 (9)의 텐서를 식 (6)에 대입한다.2) β상수를 위한 선형 방정식을 푼다.3) β 상수는 N 의 함수가 된다.4) N 에 대한 비선형 스칼라 방정식을 푼다.
일반적인 3차원 평균 유동의 해를 위한
나머지 상수들은 모두 0이며 분모의
식 (11)과 (12)로부터 얻어지는 6차 방정식은 식 (13)과 같이 나타낼 수 있다.
위의 6차 방정식은 닫힌 해 형태로 풀 수 없기 때문에 3차원 방정식의 perturbation solution을 만들어 구할 수 있으며, 그 결 과는 다음과 같다.
여기서 V= ⅡsⅡΩ/2+ϕ2이다.
각각의
2.3 Streamline curvature correction
EARSM에서는 weak equilibrium 가정을 통하여 대류항을 무시하여 식을 전개하였다. 하지만 굴곡진 표면, 정체점 주변, 박리점 근처에서는 streamline curvature 효과가 크게 작용하여 이러한 가정을 그대로 적용하는데 무리가 따른다. Girimaji (1997)와 Sjogren (1997)은 일반적인 curvilinear 좌표계에서 weak equilibrium 가정을 적용하여 추가의 대수항을 이용하여 EARSM에서 쉽게 적용하는 방법을 보였다. 식 (6)의 Ω대신 유체 입자를 따라가는 좌표계의 회전률(rotation rate)과 직접적으로 관계를 갖는 Ω(
여기서 텐서 Ωs 는 좌표계가 회전하는 양을 나타내는 것으로 비회전 좌표계(irrotational frame)에서는 무시할 수 있다. Ω(
여기서 회전률 벡터 ω(
EARSM은 유효 난류 점성계수(effective turbulent viscosity)
식 (1)의 레이놀즈 응력항은 유효 난류 점성계수와 extra anisotropy로 표현된다. 2-방정식 모델에서 사용되는 난류 점성 계수는 식 (20)으로 바뀌고, extra anisotropy는 완전히 분리된 쏘오스 항으로 다음과 같이 처리한다.
변경이 필요한 항은 난류 운동 에너지(turbulent kinetic energy)의 생성항(production)과 난류 모멘텀 수송량(turbulent transport of momentum) 부분이다. EARSM에서 생성항은 식(23)과 같이 새롭게 정의되는데 난류 운동 에너지 생성항의 기존 정의는 그대로 유지하면서 extra anisotropy의 기여 부분을 추가하는 방식을 사용한다.
여기서 P(2
다음으로 변경되어야 할 항은 모멘텀 방정식의 난류 모멘텀 수송량 부분이다. EARSM에서 이 항은 단순히 2-방정식 모델의 해당 항에 extra anisotropy의 영향을 추가함으로써 식 (24)와 같이 구할 수 있다.
본 연구에서는 2010 Gothenburg CFD workshop (Gothenburg, 2010)에서 비교 선형으로 사용된 KVLCC2와 KCS를 이용하여 EARSM에 대한 검증을 수행하였다. 비교는 2-방정식 모델로서 realizable 𝒌−𝛜 모델, EARSM, EARSM에 curvature correction을 적용한 3가지 모델과 2010 CFD workshop에서 비교 자료로 사용된 실험 결과를 이용하여 수행하였다. 모든 그래프에서는 실험 결과를 EFD, 2-방정식 모델을 RKE, EARSM을 EARSM, curvature correction을 적용한 EARSM을 EARSMCC로 표기하였다. 계산에 사용된 격자는 270만개에서 300만개 수준이다. 참고로 2010 CFD workshop에서 WAVIS2.2에 대한 V&V를 통해서 200만개 수준의 medium 격자 이상에서 충분한 정도를 확인한 바있다. 선체 표면과 만나는 첫 번째 셀의 거리는 y+ 약 80으로 설정하였다. 세 모델 모두 벽함수(wall function)를 적용하였다. EARSMCC의 경우, curvature correction의 정도를 나타내는 식(17)의
KVLCC2 모델에 대하여 자유 표면을 적용하지 않은 경우에 해당한다. 프로펠러 평면 근처에서 후류 분포, 난류 운동 에너지, 레이놀즈 응력 등 비교적 자세한 비교가 수행되었다. Table 1은 계산 조건에 대한 세부 사항을 보여주고 있으며, Table 2는 계산으로 얻어진 저항 계수들을 비교한 것이다.
[Table 1] Calculation conditions (KVLCC2 double model)

Calculation conditions (KVLCC2 double model)
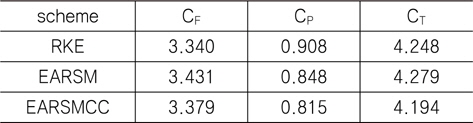
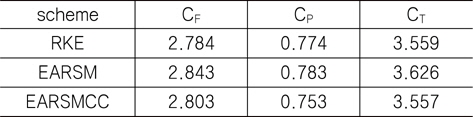
[Table 2] Resistance coefficients (KVLCC2 double model)
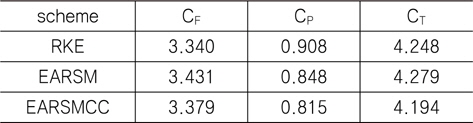
Resistance coefficients (KVLCC2 double model)
총 저항(CT) 측면에서 보면, EARSM이 RKE에 비해 약간 높은값을, EARSMCC가 약간 낮은 값을 주고 있으나, 그 차이는 약 1% 이내를 보여주고 있다. Fig. 1은 x/Lpp=0.85인 단면에서의 축방향 속도 분포를 보여주고 있다. RKE 방법에서 속도 1에 대한 등속도선이 다른 방법들에 비해 조금 수축되어 있는 점을 제외하고는 큰 차이를 발견할 수 없다.
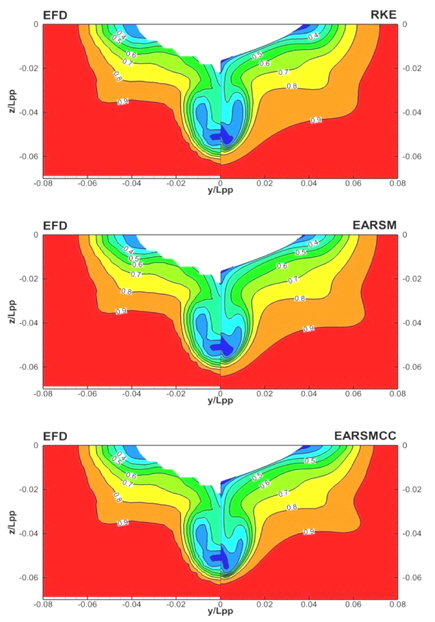
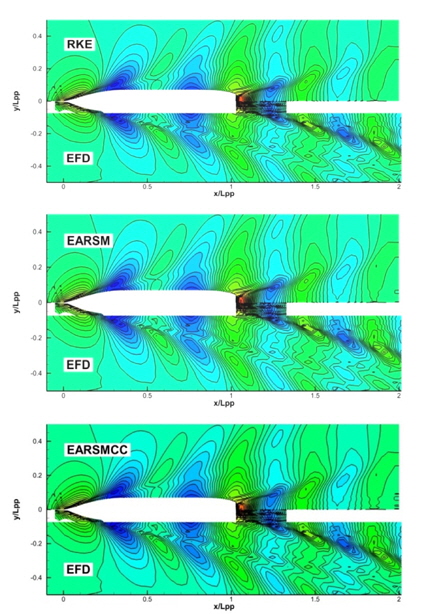
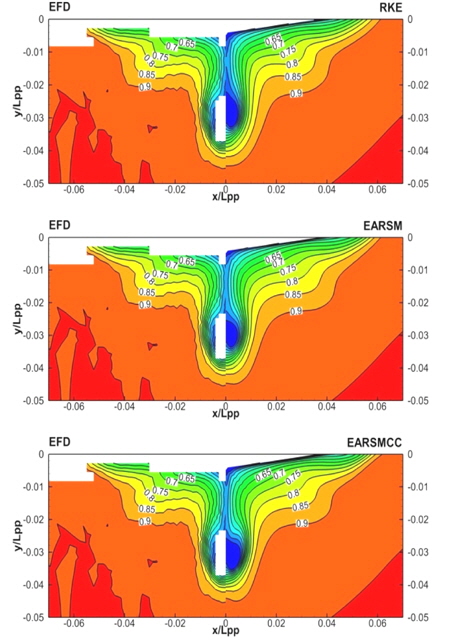
Fig. 2는 프로펠러가 위치하는 평면에서의 축방향 속도 분포를 비교한 그림이다. RKE의 경우 빌지 보텍스에 의한 갈고리 모양 등속선(hook shape)은 잘 보여주고 있으나 실험 결과와 비교할때, 등속도선들이 수축되어 있는 것을 볼 수 있다. EARSM의 경우 갈고리 모양은 조금 약하지만, RKE에 비해 덜 수축된 등속도선을 보여주고 있다. EARSMCC는 갈고리 모양 등속선과 등속도선을 모두 실험 결과와 유사하게 예측하는 것을 알 수 있다.
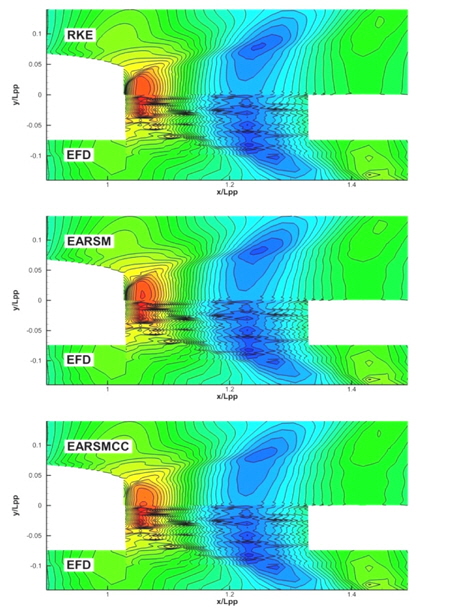
Fig. 3은 선미 후류 방향의 x/Lpp=1.1인 위치에서의 축방향 속도 분포를 나타낸다. 앞선 결과들과 마찬가지로 RKE는 실험에 비해 상당히 수축된 형상을 보여주는 반면, EARSM을 적용한 결과들은 실험값에 더 가까운 형태를 보여주고 있다.
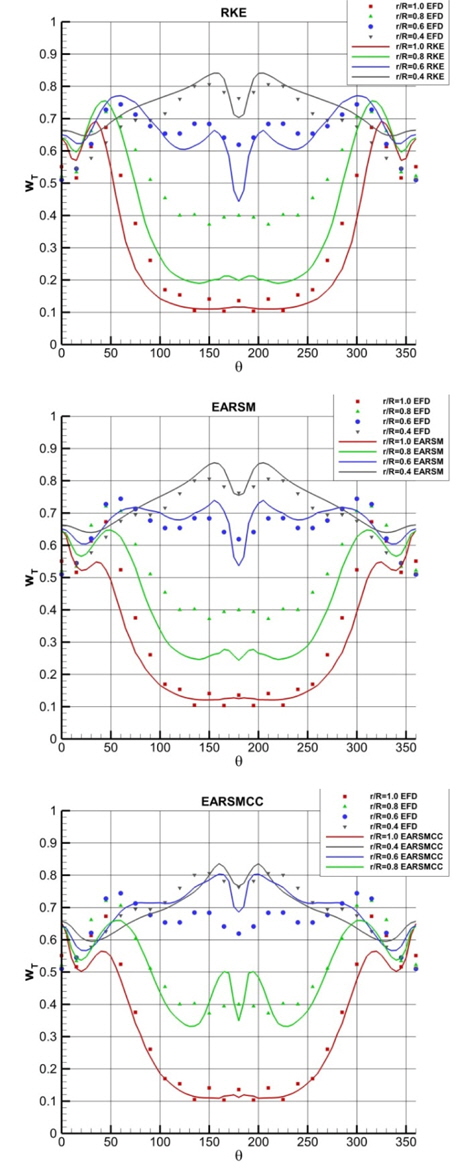
Fig. 4는 프로펠러 평면에서의 총 반류 분포(total wake fraction; wT)를 보이고 있다. 각각의 심볼과 선은 프로펠러의 0.4, 0.6, 0.8, 1.0 반경에서 얻어진 값을 나타낸다. θ는 원주 방향 각도로 수직 상방인 0도에서 반시계 방향으로 돌아가는 각도를 의미한다. 프로펠러 축의 중심선은 z/Lpp=-0.04688에 위치한다.
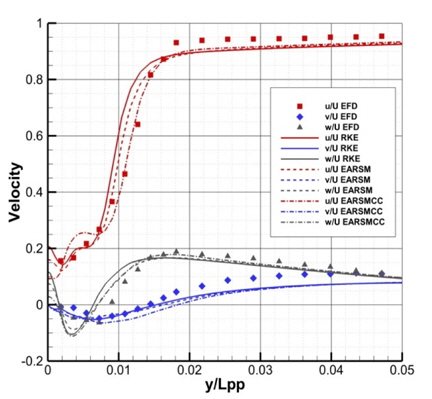
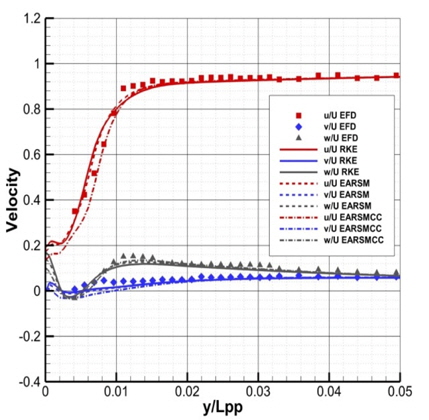
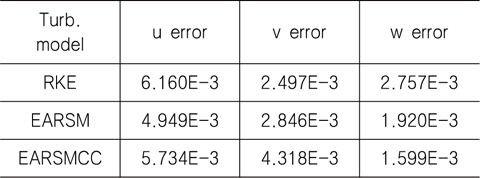
RKE의 경우 비교적 실험 결과와 일치하는 모습을 보이는데, r/R=0.8에서는 예측의 정확성이 떨어지는 모습을 보인다. 반면, EARSM을 사용한 모델에서는 조금 더 실험 결과와 가깝게 예측함을 볼 수 있다. 이는 RKE를 사용할 경우, 선미에서 실제보다 더 가속된 반류장이 얻어진다고 볼 수 있다. 총 반류 분포의 경우, curvature correction을 사용한 모델이 가장 실험 결과와 유사한 결과를 주는 것을 확인할 수 있다. Fig. 5는 프로펠러 평면에서 z/Lpp=-0.05075인 위치에서의 세 가지 속도 성분(u, v, w)을 그래프로 나타낸 것이다. y/Lpp는 0에서 0.05까지 범위를 갖는다. y/Lpp가 0.01에서 0.02 사이 구간에서 RKE로 계산한 축방향 속도(u)가 실험값보다 큰 값을 보여주고 있는데 비해 EARSM을 사용한 결과들은 그 차이가 작음을 알 수 있다. 이는 Fig. 2에서 RKE의 등속도선이 수축되어 있는 결과와 일치한다. 대략적으로 프로펠러가 위치하는 y/Lpp가 0.02보다 작은 구간에서 실험값과의 차이를 L2-norm으로 구해보면 Table 3과 같다. 특히 속도 성분중 가장 큰 부분을 차지하는 축방향 속도의 경우 EARSM 모델들이 RKE에 비해 좋은 결과를 주는 것을 확인할 수 있다.
[Table 3] Calculated error using L2-norm (KVLCC2 double model)
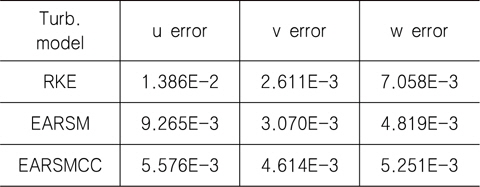
Calculated error using L2-norm (KVLCC2 double model)
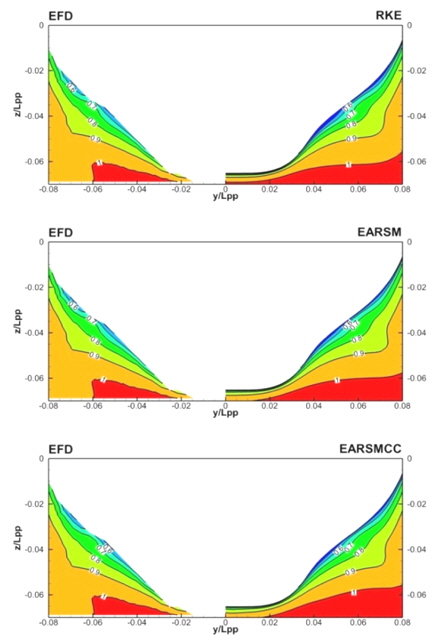
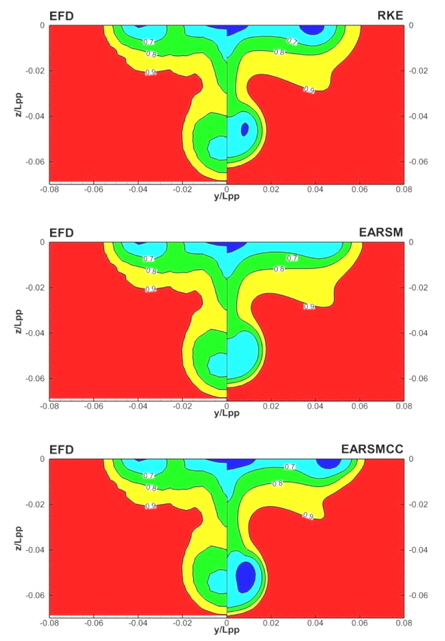
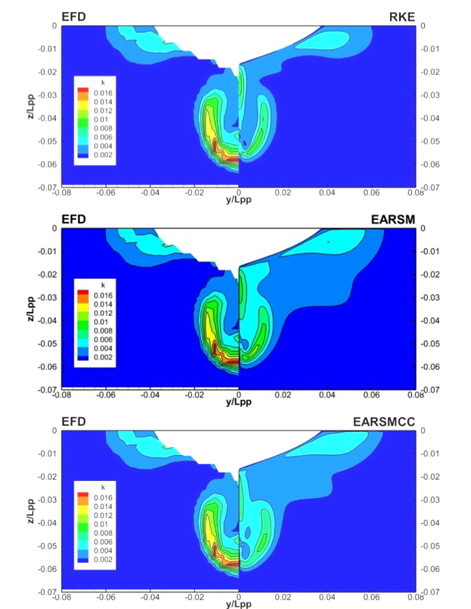
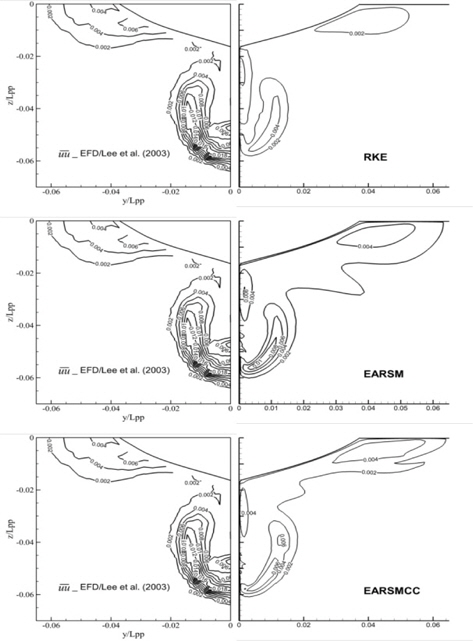
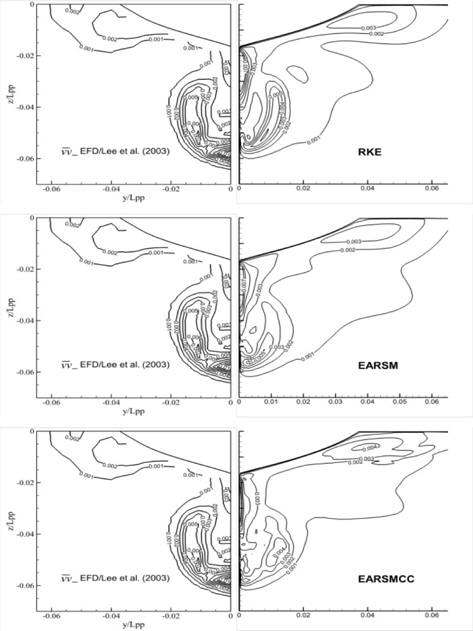
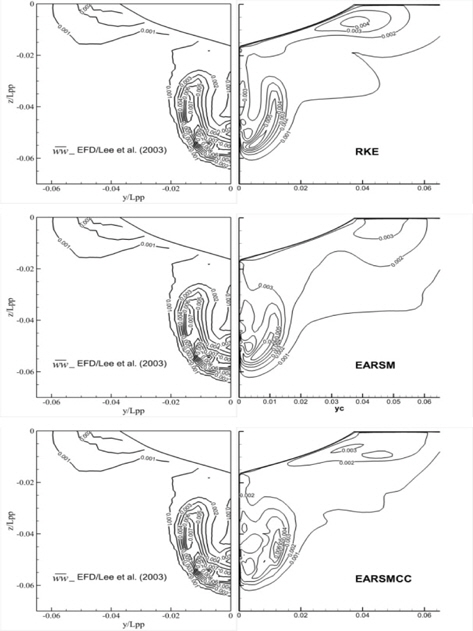
Fig. 6~9는 프로펠러 평면에서의 난류 운동 에너지와 레이놀즈 응력항들을 나타낸 그림이다. 난류 운동 에너지를 보면, 계산 결과들 모두 실험 결과보다 최대값을 작게 예측하고 있음을 알 수 있다. 다만, RKE와 EARSM은 등고선 모양을 비교적 잘 유지하고 있는데 비해 EARSMCC의 경우는 깨끗한 모양을 보여주고 있지 않은데, 이는 curvature correction을 적용할때, 식 (19)와 같이 속도의 미분, 가속도의 미분 항이 필요하게 되는데 이 부분에서 포함되는 안정성의 저하에 기인하는 것으로 생각된다. 실제로 EARSMCC의 경우, 해의 수렴도가 다른 두 방법에 비해 저하되는 것을 볼 수 있었다. 레이놀즈 응력의 경우도 난류 운동 에너지의 경우와 마찬가지로 계산 결과들의 최대값이 실험결과보다 작게 계산되었다. 공통적으로 EARSMCC가 다른 방법들에 비해 고르지 않은 분포를 보이며, 값의 차이도 컸다. RKE와 EARSM은 비슷한 수준의 결과를 보여주고 있다. 계산 결과들이 실험치에 비해 작은 값들을 주는 이유는 본 연구에 사용한 난류 모델들이 비록 기존의 2-방정식 모델에 비해 고차의 난류 모델이지만, 여전히 실제 유동 물리량을 모두 포함할 수 있는 모델로 판단하기에 다소 부족함이 있음을 반증하는 것으로 생각된다.
KVLCC2 모델에 대하여 자유 수면을 적용한 경우에 해당한다. 격자수는 double model과 일치하고 자유 수면이 포함되어 있기때문에 그 분포는 약간 상이하다. 파형 분포(wave contour) 및 일정 위치에서의 파형(wave profile)에 대한 비교가 수행되었다. Table 4는 계산 조건에 대한 세부 사항을 보여주고 있다.
[Table 4] Calculation conditions (free surface model)

Calculation conditions (free surface model)
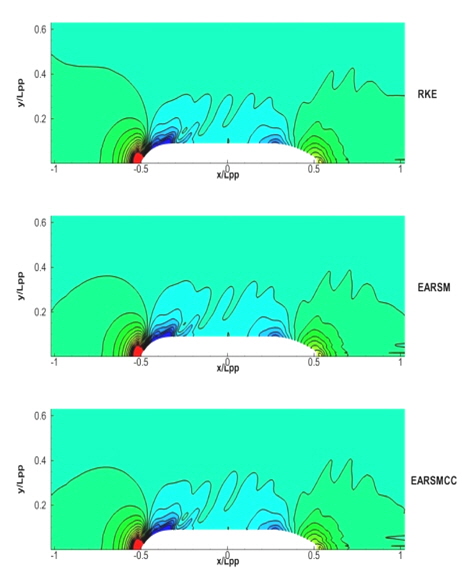
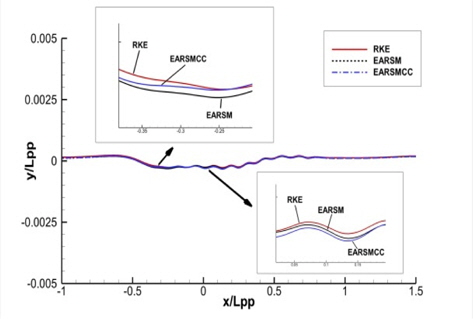
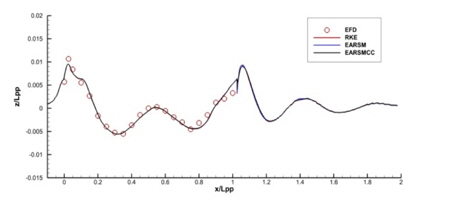
Fig. 10은 파형 분포를 비교한 그림이다. 세 가지 방법에서 특별한 차이점이 보이지 않는다. 자유 수면 부근에 충분한 격자를 넣지 않아서 실제 실험에서 보여지는 작은 파가 잡히지 않는 현상을 볼 수 있다. 이는 충분한 격자수를 사용하면 해결되는 문제로 생각된다.
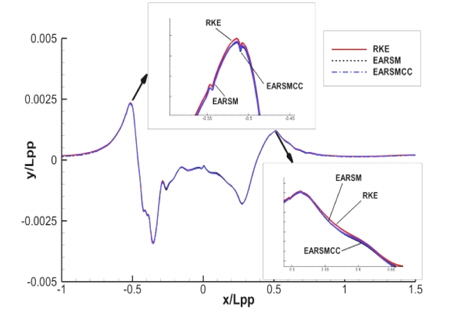
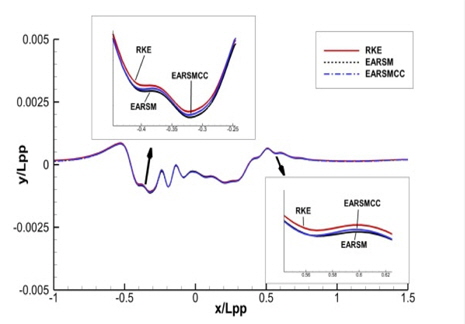
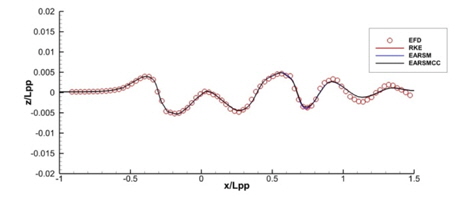
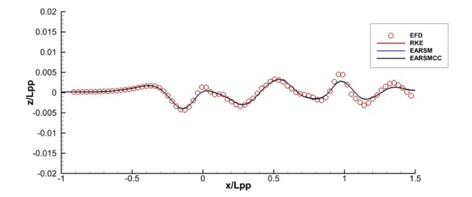
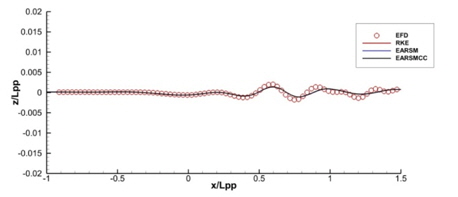
y/Lpp=0.0964, 0.1581, 0.2993인 위치에서의 파형 비교를 Fig. 11~13에 보인다. EARSM과 curvature correction 모델은 일부 구간에서의 근소한 차이를 제외하면 파형에 거의 영향을 주지 않는 것을 확인할 수 있다.
KCS 모델에 대하여 자유 수면을 적용한 경우에 해당한다. 파형 분포와 특정 위치의 파형, 프로펠러 평면 근처에서 속도 분포에 대한 비교가 수행되었다. Table 5는 계산 조건에 대한 세부사항을 보여주고 있으며, Table 6은 계산으로 얻어진 저항 계수들을 비교한 것이다.
[Table 5] Calculation conditions (KCS)

Calculation conditions (KCS)
[Table 6] Resistance coefficients (KCS)
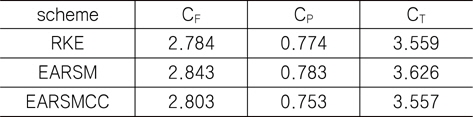
Resistance coefficients (KCS)
총 저항 측면에서 보면 KVLCC2의 경우와 마찬가지로 EARSM과 curvature correction 모델은 RKE의 결과와 약 2% 이내의 차이를 보여주고 있다. Fig. 14는 파형 비교를 보인 그림이다. KVLCC2의 경우와 마찬가지로 전체적인 파의 형상은 세 가지 방법간의 차이가 거의 없음을 알 수 있다. 트랜섬 뒤쪽의 파형 비교를 Fig. 15에 보이고 있다. EARSMCC가 다른 두 방법과 약간의 차이를 보여주고 있지만 주목할 만한 수준은 아닌 것으로 판단된다. Fig. 16~19는 각각 선체 표면에서의 파형과 y/Lpp=0.0741, 0.1509, 0.4224인 위치에서의 파형을 보여주는 그래프이다. 후류 쪽에서 실험 결과와의 차이가 공통적으로 보이는데, 이는 EARSM만의 문제라기 보다는 KVLCC2의 경우와 마찬가지로 격자의 질 문제로 보인다. 하지만, 나머지 부분에서는 실험 결과를 비교적 잘 예측하는 것을 볼 수 있다.
Fig. 20은 프로펠러 평면상의 축방향 속도 분포를 비교한 그림이다. KVLCC2의 경우와 유사하게 RKE는 실험 결과에 비해 저속영역이 약간 수축된 결과를 보여주고 있고, EARSM은 조금 더 개선된 결과를 보여준다. 하지만, EARSMCC는 다소 과장된 저속영역을 보여주는 것이 특이할 만 하다. Fig. 21은 프로펠러 평면의 일정 z위치(z/Lpp=-0.0302)에서의 속도의 세 성분을 비교한 그래프이다. EARSM이 미세하게 실험값에 근접한 결과를 주고있으며, 축방향 속도로 보았을 때, EARSMCC는 선체 중심쪽 (y/Lpp<0.006)에서 과장된 결과를 보여주고 있다. y/Lpp가 0.02보다 작은 구간에서 실험값과의 차이를 L2-norm으로 구해보면 Table 7과 같다. KCS가 KVLCC2에 비해 날씬한 선형이며, 빠른 속도 조건으로 선미 유동이 상대적으로 가속되는 상황이 되어 난류 모델 변경에 대한 효과가 상대적으로 작은 것을 확인할 수 있다.
[Table 7] Calculated error using L2 norm (KCS)
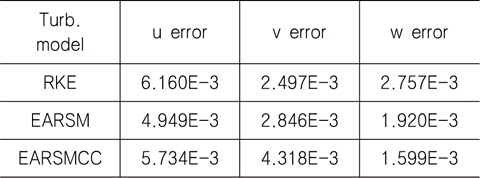
Calculated error using L2 norm (KCS)
본 연구에서는 기존의 2-방정식 모델이 갖는 단점들을 보완하기 위해 제안된 EARSM을 선박의 유체 성능 해석에 적용하였다. EARSM은 RSM의 장점을 어느 정도 취하면서 계산 속도와 강건성을 향상시킨 방법이다. 기존의 standard 𝒌 − 𝛜 모델을 사용하면서, 비등방성 레이놀즈 응력 항을 추가로 적용하는 방식을 사용하였다. 세 가지 다른 난류 모델을 사용하여 선체 주위의 유동장 및 선박 저항에 대한 비교를 수행하였다.
전반적으로, 세 가지 난류 모델들이 총 저항에 미치는 영향은 2% 이내로 크지 않았으며, 자유 수면 계산에도 큰 차이를 보이지않았다. EARSM의 계산 시간은 RKE 대비 약 10~20% 정도 증가하는 수준으로 계측되었다. RKE가 선미 유동장에서 실험 결과보다 수축된 저속 영역을 보여주는데 비해 EARSM을 적용한 방법들은 실험 결과와 조금 더 일치하는 모습을 보였다. 이는 선미 쪽의 형상으로 인한 효과를 EARSM 쪽이 잘 잡아내기 때문이라 생각된다. KVLCC2의 경우, EARSM은 예상과는 다르게 축방향 속도 분포상에서 볼 때, 기존 방법대비 갈고리 모양 등속도선 예측에서 좋은 결과를 보여주지 못했으나, 프로펠러 평면의 반류 분포, 속도 성분 등의 세밀한 결과 비교에서는 정량적으로 기존 방법보다 더 나은 결과를 보여주었다. Curvature correction을 적용한 EARSMCC는 반류 분포, 속도 성분 예측에서 좋은 결과를 보여주었지만, 레이놀즈 응력 값들이 correction의 영향으로 불안정하여 깨끗한 결과를 보여주지는 못하였다. 또한 correction의 영향을 결정하는 상수의 선택에 따라 결과가 조금씩 달라지기 때문에 최적의 값을 찾는 것도 중요하다고 생각된다. 정리하면, EARSM은 RSM에 비해 적은 계산 시간으로 기존의 2-방정식 모델들이 고려하지 못하는 레이놀즈 응력의 비등방성 항들을 고려할 수 있다는 장점을 갖고 있지만, 정식화 과정에서 도입된 가정들에 의하여 RSM에 비하여 모든 유체역학적 물리량 특성을 반영하지는 못하는 단점 또한 갖고 있다. 하지만 짧은 계산 시간과 강건성으로 인하여 RSM을 대체할 수 있는 충분한 가능성을 갖고있다고 판단된다. 본 연구에서는 기존의 벽함수를 그대로 사용하였는데, 이에 대한 타당성 검토도 필요할 것으로 보인다. 향후, 보다 다양한 선종에 대한 적용을 통해서 EARSM의 특성을 파악하고 정도를 높이기 위한 연구와 코드 최적화를 통한 계산 시간단축 또한 필요하다. 격자 의존성에 대한 검토 역시 향후 수행할 내용중의 하나이다.