The improvements of embedded processors make future technologies including wireless sensor network and internet of things feasible. These applications firstly gather information from target field through wireless network. However, this networking process is highly vulnerable to malicious attacks including eavesdropping and forgery. In order to ensure secure and robust networking, information should be kept in secret with cryptography. Well known approach is public key cryptography and this algorithm consists of finite field arithmetic. There are many works considering high speed finite field arithmetic. One of the famous approach is Montgomery multiplication. In this study, we investigated Montgomery multiplication for public key cryptography on embedded microprocessors. This paper includes helpful information on Montgomery multiplication implementation methods and techniques for various target devices including 8-bit and 16-bit microprocessors. Further, we expect that the results reported in this paper will become part of a reference book for advanced Montgomery multiplication methods for future researchers.
Public key cryptography applications are commonly used for secure and robust network services. To implement the related protocols, we need to design efficient cryptographic arithmetic operations over finite fields. Among these field arithmetic operations, multi-precision multiplication and squaring are the most expensive ones; therefore, we need to focus on an optimal implementation of these operations for resource-constrained devices, such as RFID and sensor networks. Many multiplication and squaring methods have been proposed thus far to reduce execution time and computational cost by optimizing the number of memory access and arithmetic operations. In the case of multiprecision multiplication, first, a school-book method called operand scanning, which loads all operands in a row and computes the result simultaneously, is directly implemented on embedded microprocessors. The alternative product scanning method computes all partial products in a column and does not need reload the intermediate results [1]. The hybrid method combines the useful features of both operand scanning and product scanning [2]. By adjusting the row and column widths, we can reduce the number of operand accesses and result updates. This method has an advantage over a microprocessor equipped with many general-purpose registers. In Workshop on CHES 2011, an operand caching method, which reduces the number of load operations by caching the operands, was presented [3]. Later, on the basis of this operand caching method, Seo and Kim [4] proposed the consecutive operand caching method, which is a continuous operand caching process.
With respect to an efficient multi-precision squaring operation, most of the proposed multiplication methods can be directly applied to squaring; nevertheless, doing so is not a very good idea as it is not necessary to compute all partial products and load both operands for the squaring operation. The first of these squaring methods is based on operand scanning for a hardware environment [5]. However, an embedded software implementation is conducted on resource-constrained devices, and thus, a long word sizebased hardware approach is not favorable. Thereafter, a carry-catcher squaring method was developed; this method removes the carry propagation, thereby generating carry values to the most significant byte position in a word-toword multiplication by introducing a storage for saving the carry values [6]. In 2012, the lazy doubling method, the fastest squaring algorithm thus far, was proposed in [7]. In this technique, the byte-wise multiplication results, which should be added twice, are doubled after they are collected in the accumulation registers at the end of each column computation. In [8], the sliding block doubling method was proposed. This method delayed the doubling process to the very end of the execution and the remaining partial products were executed with the doubling process.
The main difference between plain multiplication and modular multiplication is that modular multiplication and squaring computations go through a reduction process after completing the multiplication or squaring computations. A widely used reduction algorithm is Montgomery reduction. This method efficiently replaces a reduction operation by a multiplication operation. Ordinary Montgomery multiplication is efficient for the RSA cryptosystem, but this method is not favorable for elliptic curve cryptography (ECC) because multiplication is more expensive than fast reduction. Recently, optimal prime field-based Montgomery multiplication was proposed. This method overcomes the drawbacks of normal Montgomery multiplication for ECC by introducing a low-hamming-weight finite field. As a result, many multiplication operations are removed and the multiplications are simply replaced by addition.
The rest of this paper is organized as follows: in Sections II and III, we explore the core operations of Montgomery multiplication, namely multi-precision multiplication and squaring. In Sections IV and V, we discuss Montgomery multiplication and optimal prime field Montgomery multi-plication, respectively. In Section VI, we evaluate the performance of the abovementioned methods on various platforms. Finally, in Section VII, we conclude this paper.
II. MULTI-PRECISION MULTIPLICATION
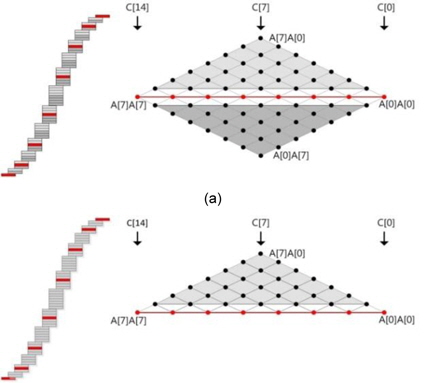
In this section, we introduce various multi-precision multiplication techniques, including operand scanning, product scanning, hybrid scanning, operand caching, and consecutive operand caching. Each method has unique features for reducing the number of load and store instructions and arithmetic operations. To describe the multi-precision multiplication method, we use the following notations. Let A and B be two operands with a length of m bits that are represented by multiple-word arrays. Each operand is written as follows: A = (A[n - 1], A[2], A[1], A[0]) and B = (B[n - 1], B[2], B[1], B[0]), where n = ⌈m/w⌉ and w denotes the word size. The result of the multiplication is twice as large as operand C = (C[2n - 1], C[2], C[1], C[0]).
For the sake of clarity, we describe the abovementioned method by using a multiplication structure and rhombus form. As shown in Fig. 1, each point represents a multiplication A[
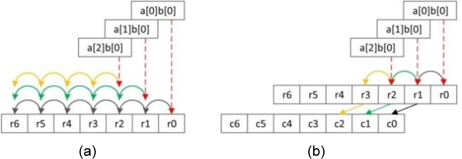
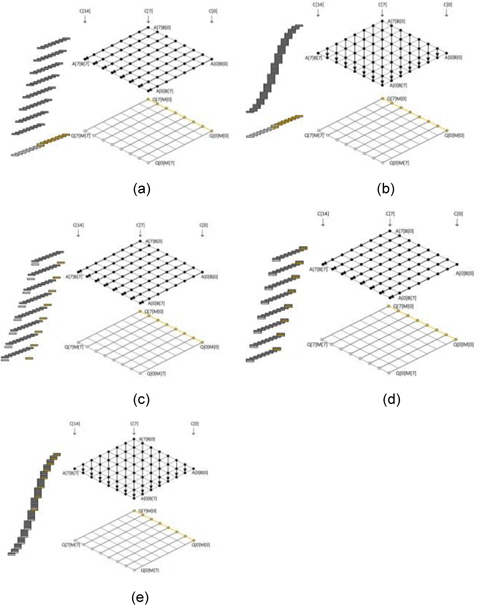
The squaring method can be implemented using the existing multiplication techniques because squaring requires almost the same operations as those required for multiplication, such as memory access and arithmetic operations. However, there are two main differences between multiplication and squaring; these are illustrated in Fig. 2. First, only one operand (A) is used for the squaring computation; therefore, the operand load is reduced to half of that in the case of multiplication and many registers that were previously used for operand holding are assigned the idle status and can be used for caching intermediate results or other values. Second, some duplicate partial products exist. In Fig. 2, the squaring structure consists of three parts, namely a red dotted middle part and light and dark gray triangle parts. The red part denotes the multiplication of the same operand, which is computed once. The other parts, namely the light and dark gray parts, generate the same partial product results. Therefore, these parts are multiplied once and added twice to the intermediate results. This computation generates the correct results, as expected. After removing the duplicate partial product results, we can describe the squaring structure as a triangular form, as shown in Fig. 2. Fig. 3(a) describes Yang et al.’s method [5]. This squaring method is intended for a hardware machine and not for a software implementation. Therefore, the software implementation has several disadvantages, such as an insufficient number of general-purpose registers to store all operands, carry-catcher values, and intermediate results obtained during partial product computations using operand scanning. Furthermore, reloading and restoring the intermediate results for doubling require many memory access operations. Thus, the straight-forward implementation of the squaring method used for hardware is not recommended for software. Prime field multiplication consists of a number of partial products. When we compute partial products in an ascending order, intermediate results generate carry values, accumulating the partial product results. Traditionally, carry values spread to the end of the intermediate results, as shown in Fig. 4(a). This case continuously updates the result register (r6_r0), and therefore, the addition arithmetic is used many times. To reduce the overhead, the carry-catcher method for storing carry values to additional registers (c6_c0), was presented in [6] and is illustrated in Fig. 4(b).
The carry-catching registers are immediately updated at the end of a computation. The carry-catcher-based squaring, illustrated in Fig. 3(b), was introduced in [6]. This method follows hybrid scanning and doubles the partial product results before they are added to the results. This method is inefficient because all products need to be doubled. The lazy doubling method, shown in Fig. 3(c), is an efficient doubling method and is described in detail in [7].
This method also follows a hybrid scanning structure; therefore, the constant size of the operands and the inner structure is computed and the carry-catcher method is used for removing the consecutive carry updates. An important advantage of this method is the doubling process, which is delayed to the end of the inner structure and then computed.
This method reduces the number of arithmetic operations by conducting doubling computations on the accumulated intermediate results. This technique significantly reduces the number of doubling processes to 1. In [8], the sliding block doubling method is proposed. This method delays the doubling process to the very end of the implementation and the remaining partial products are executed with the doubling process. Since the doubling operation is conducted with the accumulated results, the number of arithmetic operations is efficiently reduced.
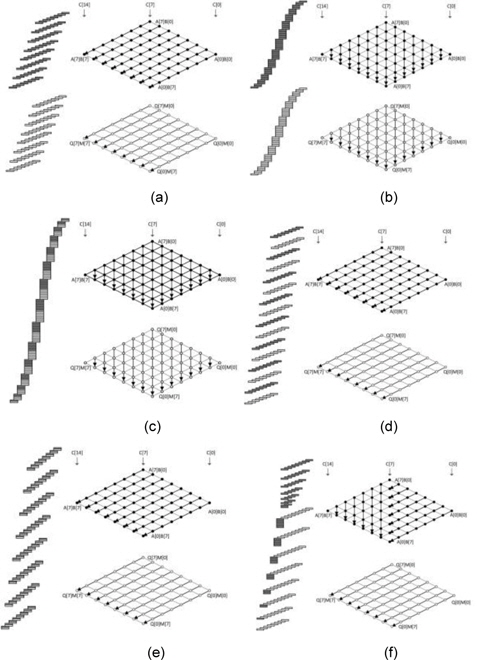
The Montgomery algorithms were first proposed in 1985 [9]. Montgomery algorithms avoid division in modular multiplication and reduction by introducing simple shift operations. Given two integers A and B and the modulus M, to compute the product P = A ∙ B mod M, in the Montgomery method, the original operands A and B are converted into the Montgomery domain, A′ = A ∙ R mod M and B′ = B ∙ R mod M. For efficient computation, the Montgomery residue R is selected as a power of 2 and the constant M′ = −𝑀−1 mod 2𝑛 is pre-computed. To compute the product, the following three steps are performed: P = A ∙ B , Q = P ∙ M′ mod 2𝑛 , Z = (P + QM) /2𝑛 . There are many variants of the Montgomery method. In Fig. 5, we illustrate the basic structure of Montgomery multiplication. In order to appropriately describe Montgomery multiplication, we introduce the double rhombus form.
The upper rhombus represents Montgomery multiplication and the under rhombus, Montgomery reduction. To distinguish both computations, we have denoted the product process in dark gray and the reduction process in white. Montgomery multiplication has two main modes. The first mode is the separated version shown in Fig. 5(a) and (b). This method separates the multiplication and the reduction processes. The second mode is the interleaving version shown in Fig. 5(c)–(f). This model combined multiplication and reduction. If multiplication and reduction are partly integrated, we call the mode the coarsely integrated mode, and if the operations are fully integrated, we call the mode the finely integrated mode. The first separated operand scanning (SOS) method computes the products and the reduction result separately.
The multiplication structure is simple, but the performance is highly degraded because the operand scanning method frequently accesses the memory to load or store the intermediate results and operands. The separated product scanning method performs the product scanning method for multiplication and reduction processes separately. As compared to that in SOS, in this method, the required number of registers is small; therefore, this method is a better choice when it comes to register-constrained devices. The coarsely integrated operand scanning (CIOS) method improves the previous SOS method by integrating the multiplication and reduction steps. Instead of computing all the full multiplication processes separately, the multiplication and reduction steps are alternated in every loop. With this technique, we can update the intermediate results more efficiently. In the case of CIOS, two inner loops are computed, but the finely integrated operand scanning (FIOS) method integrates the two inner loops of multiplication and reduction and computes one inner loop. This method reduces intermediate result load and store operations by computing all results at the intermediate stages. The finely integrated product scanning (FIPS) method is used for performing product scanning multiplication and reduction in the integrated model. This method does not reload the intermediate results; therefore, it is more efficient than the FIOS method. The coarsely integrated hybrid scanning method adopts hybrid multiplication.
The first half of the multiplication is conducted with product scanning; then, multiplication and reduction are coarsely integrated in the operand scanning methods. Recently, [10] discussed the performance of different Montgomery multiplications on an 8-bit AVR microcontroller and analyzed the exact computation complexity at the instruction level. The authors of [10] discussed different hybrid Montgomery multiplication algorithms, including hybrid finely integrated product scanning (HFIPS), and introduced a novel approach for Montgomery multiplication, which we call hybrid separated product scanning (HSPS). This method finely reschedules the inner structure to reduce the number of data transfer instructions.
V. OPTIMAL PRIME FIELD MONTGOMERY MULTIPLICATION
A special family of prime fields, called optimal prime field (OPF), was proposed in [11]. The n-bit OPF primes have the following form: M = u ∙ 2k + 𝑣. Let u and v be relatively small coefficients as compared to 2k; u is either 8-bit or 16-bit long, and v is several bits long.
Character k denotes n - m ∙ w, where m denotes a small integer, and m ∙ w represents the size of u. The OPF in [11] set u as a 16-bit-long integer and v as 1; this is formalized as M = u ∙ 2𝑛−16 + 1. Most of the OPF prime bits are 0 except a few bits in the most and least significant words. Due to the low hamming weight of OPF, Montgomery multiplication is considerably simpler than its ordinary counterparts. To describe the OPF model, we introduced two colored dots in Fig. 6. The first yellow dot describes the addition of Q to the intermediate results because parameter M has one in the least significant bit, which is computable with a simple addition operation instead of partial products. In the case of the white dot, 16-bit partial products Q ∙ M are added to the intermediate results. The various curves including Weierstraß, twisted Edwards curve, and GLV using OPF are reported in [12, 13].
160 bit: 52542 × 2144 + 1
0XCD3E000000000000000000000000000000000001
192 bit: 55218 × 2176 + 1
0XD7B200000000000000000000000000000000000000000 001
224 bit: 50643 × 2208 + 1
0XC5D300000000000000000000000000000000000000000 00000000001
256 bit: 37266 × 2240 + 1
0X9192000000000000000000000000000000000000000000 000000000000000001
OPF-based Montgomery multiplication can exploit an ordinary Montgomery method without difficulty. Among the straightforward adoptions of the previous methods, OPFFIPS finely combines multiplication and reduction and reports the highest performance because the results are located in the same column, which removes the duplicate intermediate load or store operations.
>
A. Evaluation on 8-bit Platform AVR
In this section, we will describe the performance evaluation using an 8-bit AVR processor. The embedded processor is equipped with an ATmega128 8-bit processor clocked at 7.3728 MHz. It has a 128-kB EEPROM chip and a 4-kB RAM chip [14]. The ATmega128 processor has the RISC architecture with 32 registers. Among them, 6 registers (r26–r31) serve as special pointers for indirect addressing. The remaining 26 registers are available for arithmetic operations. One arithmetic instruction incurs one clock cycle, and memory instructions or 8-bit multiplication operations incur two processing cycles.
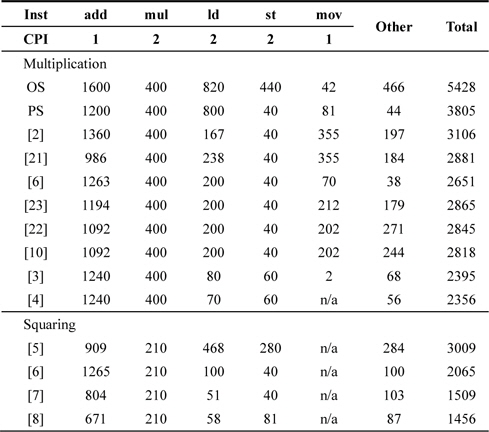
The comparison results of multiplication are presented in Table 1. In the case of the operand scanning (OS) method, intermediate results are retained in registers; therefore, operands are not cached in the registers and reloaded several times from the memory to the register. As described earlier, memory operations are the most expensive operations in RISC processors and degrade performance significantly. The alternative product scanning (PS) method reduces the number of store instructions required by using column-wise multiplication. This architecture avoids a high overhead to retain intermediate results on general-purpose registers. The remaining registers are efficiently used for caching operands. Thereafter, a hybrid scanning method that combines the efficient architectures of the previous OS and PS methods was proposed in [2]. This method adjusts the column and row widths to fit into a number of generalpurpose registers in the embedded processors. There are several hybrid scanning (HS) variants proposed in other papers, and small improvements were achieved in each of these papers. In CHES 2011, an operand caching method that caches operands in a row and significantly reduces the computational cost is proposed [3]. In Workshop on Information Security Applications 2012, an advanced operand caching (OC) method, called consecutive operand caching (COC), was presented; this method caches operands from the first row to the last row [4]. In the case of squaring, this distinct structure can be exploited to improve the performance significantly. Firstly, the operand scanning method is directly applied to the squaring method. This is faster than OS multiplication but slower than an advanced multi-plication method because of the requirement to store a large number of intermediate results. In [6, 7], duplicate parts are efficiently doubled with simple shift or addition. Further improvements are achieved in [19]. This method fully accumulates all the intermediate results and then doubles the parts with a simple shift operation; thus, the number of multiplication and arithmetic operations is decreased.
[Table 1.] Comparison of multiplication results in case of 160-bit unrolled version
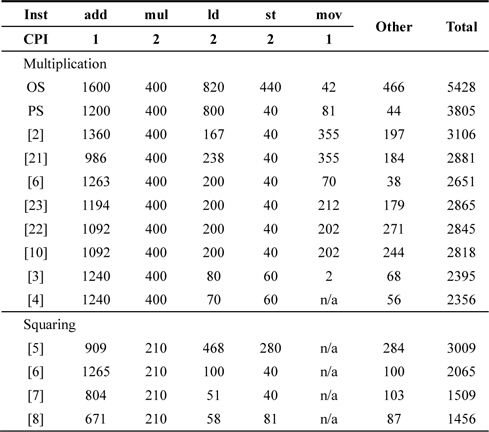
Comparison of multiplication results in case of 160-bit unrolled version
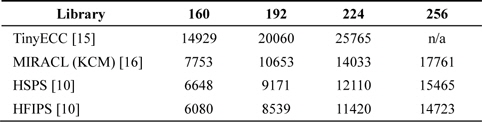
In terms of Montgomery multiplication, there are three representative results. First, TinyECC is the most referenced work and provides several ECC primitives over TinyOS [15]. The researchers of [15] adopted fast reduction for a modular operation. This technique is more efficient than any other method because programmers can hardcode the reduction process by following the target curves; however, this is not scalable architecture. In [16], a Karatsuba-based Montgomery method is introduced. This method exploits the features of the Karatsuba algorithm to reduce the number of required clock cycles. Recently, in [10], novel HSPS and HFIPS methods were presented. These methods redesign the inner loops to reduce the number of mov instructions and show the fastest performance ever achieved. The detailed clock cycle is presented in Table 2.
[Table 2.] Different length Montgomery multiplication execution time (clock cycles)
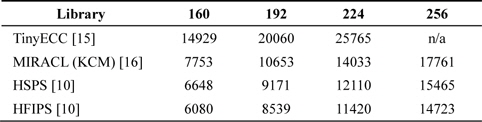
Different length Montgomery multiplication execution time (clock cycles)
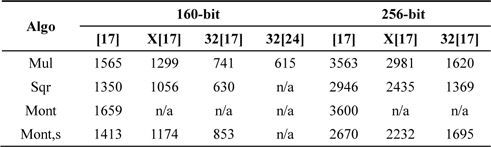
Alternative OPF-Montgomery multiplication has a low hamming weight than ordinary Montgomery multiplication. These methods exploit the FIPS method for the OPFMontgomery method. The direct implementation shows significant performance enhancements, and the squaring method shows a higher performance than the multiplication method. The detailed clock cycle is presented in Table 3.

Execution time (in cycles) of OPF-Montgomery multiplication and squaring in 160-bit on AVR
>
B. Evaluation on 16-bit Platform MSP430X
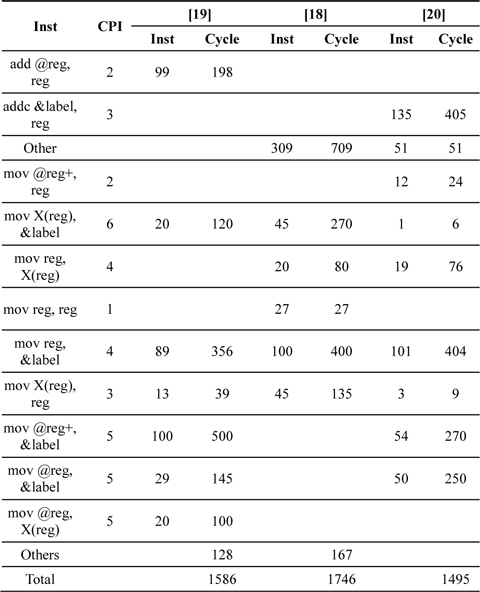
MSP430 is a representative 16-bit processor board with a clock frequency of 8 MHz [17], 32- to 48-kB ash memory, 10-kB RAM, and 12 general-purpose registers from r4 to r15 available. Among them, 2 registers serve as special pointers for indirect addressing, 4 registers for intermediate results, and the remaining 6 registers for operand caching. Unlike the AVR series, MSP430 provides an embedded 16- bit hardware multiplier that computes 16-bit real-number multiplication and multiplication and accumulation (MAC). In the MAC mode, values are multiplied and accumulated into the same location in the internal memory, yielding the final result at the same location. The latest target board, the MSP430X, operates at a higher clock frequency of 16–20 MHz and provides 32-bit multiplication. To perform multiplication, the multiplication mode is selected by allocating operands to memory maps among MPY32L, MPYS32L, MAC32L, and MACS32L. These denote multiplication modes including signed multiplication, MAC, and signed MAC. The MAC mode preserves intermediate results in the inner memory from RES0 to RES3. Only the SUMEXT value, a 65-bit result, is not maintained; therefore, it needs to be stored into a register every session. The multiplication and squaring results are presented in Table 4. First, the hybrid method is applied to upgrade performance [18]. This shows a high performance, but the latter method proposed in [19] is finely upgraded by exploiting the MAC method. This function finely accumulates all the intermediate results and updates the results immediately.
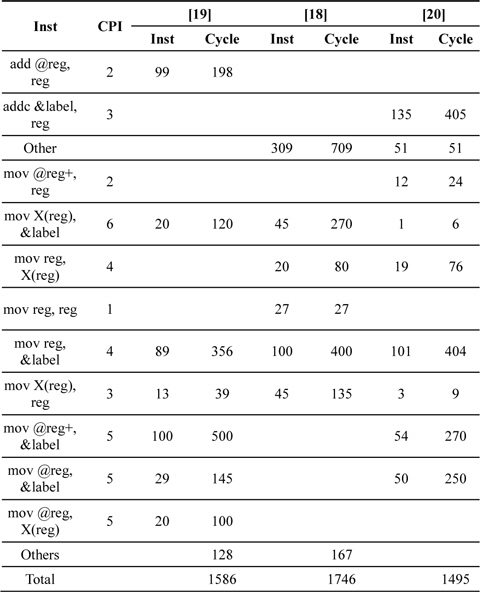
Comparison of Comba multiplication, variants of hybrid multiplication, and operand caching multiplication
Further improvements are described in [20]. The authors of [20] use fine register assignments to reduce the number of memory access operations. In the case of Montgomery multiplication, there is only one result available and the algorithm exploits the MAC-based product scanning methods. The results are presented in Table 5. In [17], the authors presented PS-based Montgomery multiplication. Its performance is better in a sparse form because this case reduces the number of arithmetic operations. Furthermore, the squaring method is faster than the multiplication method because of the duplicate partial products discussed in the previous section.
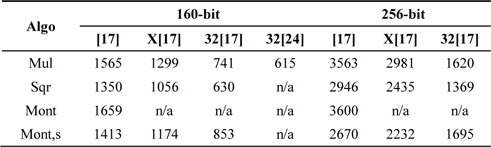
Comparison of Comba multiplication, variants of hybrid multiplication, and operand caching multiplication
In this paper, we reviewed several Montgomery multiplication methods on embedded processors. Each embedded processor has a specific architecture; therefore, the multiplication method should be carefully selected to achieve a high performance. In Table 4, we present the current stateof-the-art methods and candidate fields, which imply that there is room to improve performance by adopting advanced multiplication/squaring methods. In the case of ATmega, the most advanced multiplication and squaring methods are COC(Consecutive Operand Caching) and SBD(Sliding Block Doubling), respectively. However, for Montgomery multiplication, the PS method is still actively exploited. Therefore, we can expect performance enhancement by applying these advanced multiplication and squaring methods to Montgomery methods. In the case of MSP, because of the use of an advanced MAC method, the PS method is the best choice; therefore, all the implementations are conducted with the PS method. However, there are newly released methods including COC and SBD available. Furthermore, OPF-Montgomery multiplication and squaring have not yet been studied carefully. Therefore, we can apply PS, COC, or SBD to improve the performance.
Public key cryptography is widely used for key distribution and digital signature. However, high computational complexity is not practical for resource-constrained devices such as embedded processors. To accelerate performance in terms of speed, most expensive operations, such as finite field multiplication and squaring, should be considered. In this study, we explored various Montgomery algorithms on embedded microprocessors and analyzed each method in detail. In the evaluation part, we suggested several research topics that have not yet been studied carefully. This paper includes a discussion of a wide range of Montgomery multiplication methods for embedded microprocessors and would be a good reference paper for future researchers.
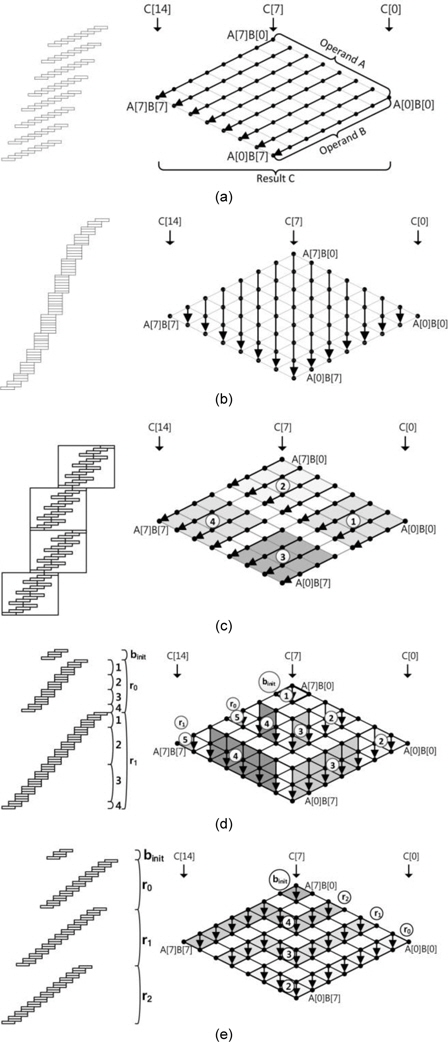
![(a) Yang et al. [5] squaring, (b) carry-catcher squaring, (c) lazy doubling squaring, and (d) sliding block doubling squaring.](http://oak.go.kr/repository/journal/14631/E1ICAW_2014_v12n3_145_f003.jpg)