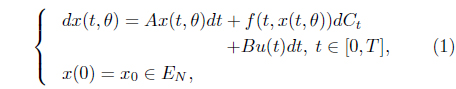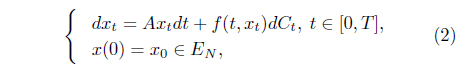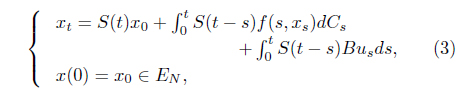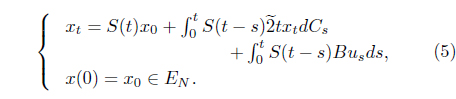The concept of fuzzy set was initiated by Zadeh via membership function in 1965. Fuzzy differential equations are a field of increasing interest, due to their applicability to the analysis of phenomena where imprecision in inherent. Kwun et al. [1-4] and Lee et al. [5] have studied the existence and uniqueness for solutions of fuzzy equations.

The theory of controlled processes is one of the most recent mathematical concepts to enable very important applications in modern engineering. However, actual systems subject to control do not admit a strictly deterministic analysis in view of various random factors that influence their behavior. The theory of controlled processes takes the random nature of a systems behavior into account. Many researchers have studied controlled processes. With regard to fuzzy systems, Kwun and Park [6] proved controllability for the impulsive semilinear fuzzy differential equation in n-dimension fuzzy vector space. Park et al. [7] studied the controllability of semilinear fuzzy integrodifferential equations with nonlocal conditions. Park et al. [8] demonstrated the controllability of impulsive semilinear fuzzy integrodifferential equations, while Phu and Dung [9] studied the stability and controllability of fuzzy control set differential equations. Lee et al. [10] examined the controllability of a nonlinear fuzzy control system with nonlocal initial conditions in n-dimensional fuzzy vector space Eⁿ_N .

In terms of the controllability of stochastic systems, P. Balasubramaniam [11] studied quasilinear stochastic evolution equations in Hilbert spaces, and the controllability of stochastic control systems with time-variant coefficients was proved by Yuhu [12]. Arapostathis et al. [13] studied the controllability properties of stochastic differential systems that are characterized by a linear controlled diffusion perturbed by a smooth, bounded, uniformly Lipschitz nonlinearity.

Stochastic differential equations driven by Brownian motion have been studied for a long time, and are a mature branch of modern mathematics. A new kind of fuzzy differential equation driven by a Liu process was defined as follows by Liu [14] dXt = f(Xt, t)dt + g(Xt, t)dCt where C_t is a standard Liu process, and f, g are some given functions. The solution of such equation is a fuzzy process. You [15] discussed the solutions of some special fuzzy differential equations, and derived an existence and uniqueness theorem for homogeneous fuzzy differential equations. Chen [16] for fuzzy differential equations. Liu [17] studied an analytic method for solving uncertain differential equations. In this paper, we extend the result of Liu [17] to fuzzy differential equations driven by a Liu process within a controlled system.

We study the exact controllability of abstract fuzzy differential equations in a credibility space:

where the state x(t, θ) takes values in X( E_N) and another bounded space Y ( E_N). We use the following notation: E_N is the set of all upper semi-continuously convex fuzzy numbers on R, (,,Cr) is the credibility space, A is a fuzzy coefficient, the state function x : [0, T] × (,,Cr) X is a fuzzy process, f : [0, T] × X X is a fuzzy function, u : [0, T]×(,,Cr) Y is a control function, B is a linear bounded operator from Y to X, C_t is a standard Liu process and x₀ E_N is an initial value.

In Section 2, we discuss some basic concepts related to fuzzy sets and Liu processes.

In Section 3, we show the existence of solutions to the free fuzzy differential equation (1)(u ≡ 0).

Finally, in Section 4, we prove the exact controllability of the fuzzy differential Eq. (1).

In this section, we give some basic definitions, terminology, notation, and Lemmas that are relevant to our investigation and are needed in latter sections. All undefined concepts and notions used here are standard.

We consider E_N to be the space of one-dimensional fuzzy numbers u : R [0, 1], satisfying the following properties: (1) u is normal, i.e., there exists an u0 R such that u(to) = 1; (2) u is fuzzy convex, i.e., u(λt+(1╶λ)s) ≥ min{u(t); u(s)} for any t, s R, 0 ≤ λ ≤ 1; (3) u(t) is upper semi-continuous, i.e., for any tk R (k = 0, 1, 2, ․ ․ ․ ), tk t0; (4) [u]0 is compact. The level sets of u, [u]^α = {t R : u(t) ≥ α}, α (0, 1], and [u]⁰ are nonempty compact convex sets in R [8].

Definition 2.1 [19] We define a complete metric D_L on E_N by for any u, v E_N, which satisfies D_L(u + w, v + w) = D_L(u, v) for each w E_N, and for every α [0, 1] where , R with ≤ .

Definition 2.2 [20] For any u, v C([0, T],E_N), the metric H₁(u, v) on C([0, T],E_N) is defined by

Let be a nonempty set, and let be the power set of . Each element in is called an event. To present an axiomatic definition of credibility, it is necessary to assign a number Cr{A} to each event A indicating the credibility that A will occur. To ensure that the number Cr{A} has certain mathematical properties that we intuitively expect, we accept the following four axioms:

(1) (Normality) Cr{} = 1. (2) (Monotonicity) Cr{A} ≤ Cr{B} whenever A B. (3) (Self − Duality) Cr{A}+Cr{Ac} = 1 for any event A. (4) (Maximality) Cr{∪iAi} = supi Cr{Ai} for any events {Ai} with supi Cr{Ai} < 0.5.

Definition 2.5 [21] Let be a nonempty set, be the power set of , and Cr be a credibility measure. Then the triplet (,,Cr) is called a credibility space.

Definition 2.6 [14] A fuzzy variable is a function from a credibility space (,,C_r) to the set of real numbers.

Definition 2.7 [14] Let T be an index set and (,,Cr) be a credibility space. A fuzzy process is a function from T × (,,Cr) to the set of real numbers.

That is, a fuzzy process x(t, θ) is a function of two variables such that the function x(t*, θ) is a fuzzy variable for each t*. For each fixed θ*, the function x(t, θ*) is called a sample path of the fuzzy process. A fuzzy process x(t, θ) is said to be sample-continuous if the sample ping is continuous for almost all θ. Instead of writing x(t, θ), we sometimes we use the symbol x_t.

Definition 2.8 Let (,,Cr) be a credibility space. For fuzzy random variable x_t in credibility space, for each α [0, 1], the α-level set is defined by where with when α [0, 1].

Definition 2.9 [22] Let 𝜉 be a fuzzy variable and r is real number. Then the expected value of 𝜉 is defined by provided that at least one of the integrals is finite.

Lemma 2.1 [22] Let 𝜉 be a fuzzy vector. The expected value operator E has the following properties: (i) if f ≤ g, then E[f(𝜉)] ≤ E[g(𝜉)], (ii) E[− f(𝜉)] = − E[f(𝜉)], (iii) if functions f and g are comonotonic, then for any nonnegative real numbers a and b, we haveE[af(𝜉) + bg(𝜉)] = aE[f(𝜉)] + bE[g(𝜉)]. Where f(𝜉) and g(𝜉) are fuzzy variables.

Definition 2.10 [?] A fuzzy process C_t is said to be a Liu process if (i) C0 = 0, (ii) Ct has stationary and independent increments, (iii) every increment Ct+s ― Cs is a normally distributed fuzzy variable with expected value et and variance σ2t2, whose membership function is , x R. The parameters e and σ are called the drift and diffusion coefficients, respectively. Liu process is said to be standard if e = 0 and σ = 1.

Definition 2.11 [23] Let x_t be a fuzzy process and let C_t be a standard Liu process. For any partition of closed interval [c, d] with c = t₀ < · · · < t_n = d, the mesh is written as . Then the fuzzy integral of x_t with respect to C_t is provided that the limit exists almost surely and is a fuzzy variable.

Lemma 2.2 [23] Let C_t be a standard Liu process. For any given θ with Cr{θ} > 0, the path C_t is Lipschitz continuous, that is, the following inequality holds |Ct1 − Ct2 | < K(θ)|t1 − t2|, where K is a fuzzy variable called the Lipschitz constant of a Liu process with and E[K^p] < ∞, ∀_p > 0.

Lemma 2.3 [23] Let C_t be a standard Liu process, and let h(t; c) be a continuously differentiable function. Define x_t = h(t;C_t). Then we have the following chain rule

Lemma 2.4 [23] Let f(t) be continuous fuzzy process, the following inequality of fuzzy integral holds where K = K(θ) is defined in Lemma 2.2.

In this section, by Definition 2.7, instead of longer notation x(t, θ), sometimes we use the symbol x_t. We consider the existence and uniquencess of solutions for the fuzzy differential Eq (1)(u ≡ 0).

where the state x_t takes values in X( E_N). E_N is the set of all upper semi-continuously convex fuzzy numbers on R, (,,Cr) is credibility space, A is fuzzy coefficient, the state function x : [0, T] × (,,Cr) X is a fuzzy process, f : [0,T] × X X is regular fuzzy function, C_t is a standard Liu process, x₀ E_N is initial value.

Lemma 3.1 [19] Let ɡ be a function of two variables and let at be an integrable uncertain process. Then a given uncertain differential equation by dXt = atXtdt + ɡ(t,Xt)dCt has a solution where and Z_t is the solution of uncertain differential equation dZt = Ytɡ(t, Y −1Zt)dCt with initial value Z₀ = X₀.

Using Lemma 3.1, we show that, for fuzzy coefficient A, the Eq. (2) have a solution.

Lemma 3.2 For x(0) = x₀, if x_t is solution of the Eq. (2), then the solution x_t is given bywhere S(t) is continuous with S(0) = I, |S(t)| ≤ c, c > 0, for all t [0, T].

Proof For fuzzy coefficient A, the following define inverse of S(t) S −1(t) = e −At. Then it follows that dS −1(t) = −Ae −Atdt = −AS −1(t)dt.Applying the integration by parts to the above equation provides That is, d(S −1(t)xt) = S −1(t)f(t, xt)dCt. Defining z_t = S ⁻¹(t)x_t, we obtain x_t = S(t)z_t and dzt = S −1(t)f(t, S(t)zt)dCt. Furthermore, we get in virtue of S(0) = I, and z₀ = x₀, Therefore the Eq. (2) has the following solution where we write S(t − s) instead of S(t)S ⁻¹(s).

Assume the following statements:

(H1) For x_t, y_t ∈ C([0, T] × (,,C_r),X), t ∈ [0, T], there exists positive number m such that dL([f(t, xt)]α, [f(t, yt)]α) ≤ mdL([xt]α, [yt]α) and f(0,X_{0}(0)) ≡ 0.

(H2) 2cmKT ≤ 1.

By Lemma 3.2, we know that the Eq. (2) have a solution x_t. Thus in Theorem 3.1, we show that uniqueness of solution for Eq. (2).

Theorem 3.1 For every x₀ ∈ E_N, if hypotheses (H1), (H2) are hold, then the eEq. (2) have a unique solution x_t ∈ C([0, T] × (,,C_r),X).

Proof For each 𝜉_t ∈ C([0, T] × (,,C_r),X), t ∈ [0, T] define Thus, one can show that 𝜉 : [0, T]× (,,C_r) C([0, T]× (,,C_r),X) is continuous, then : C([0, T] × (,,Cr),X) C([0, T] × (,,Cr),X).

It is also obvious that a fixed point of is solution for the Eq. (2). For , η_t ∈ C([0, T] × (,,C_r),X), by Lemma 2.4 and hypothesis (H1), we have Therefore, we obtain that Hence, for a.s. θ ∈ , by Lemma 2.1, By hypotheses (H2), is a contraction mapping. By the Banach fixed point theorem, Eq. (2) have a unique fixed point x_t ∈ C([0, T] × (,,C_r),X).

In this section, we study exact controllability for abstract fuzzy differential Eq. (1).

We consider solution for the Eq. (1), for each u in Y (⊂ E_N).

where S(t) is continuous with S(0) = I, |S(t)| ≤ c, c > 0, for all t ∈ [0, T].

We define the controllability concept for abstract fuzzy differential equations.

Definition 4.1 The Eq. (1) are said to be controllable on [0,T], if for every x₀ ∈ E_N there exists a control u_t ∈ Y such that the solution x of (1) satisfies x_T = x¹ ∈ X, a.s. θ (i.e., [x_T ]^α = [x¹]^α).

Define the fuzzy mapping : (R) X where (R) is a nonempty fuzzy subset of R and is closure of support u. Then there exists (i = l, r) such that We assume that , are bijective mappings.

We can introduce α-level set of u_s defined by

Then substitute this expression into the Eq. (3) yields α-level of x_T . Hence this control u_t satisfis x_T = x¹, a.s. θ.

We now set where the fuzzy mappings satisfies above statements.

(H3) Assume that the linear system of Eq. (1) (f ≡ 0) is controllable.

Theorem 4.1 If Lemma 2.4 and the hypotheses (H1), (H2) and (H3) are satisfied, then the Eq. (1) are controllable on [0, T].

Proof We can easily check that Φ is continuous from C([0, T]× (,,C_r),X) to itself. By Lemma 2.4 and hypotheses (H1) and (H2), for any given θ with C_r{θ} > 0, x_t, y_t ∈ C([0, T]× (,,C_r),X), we have

Therefore by Lemma 2.1,

We take sufficiently small T, (2cmKT) < 1. Hence Φ is a contraction mapping. We now apply the Banach fixed point theorem to show that the Eq. (3) have a unique fixed point.

Consequently, the Eq. (1) are controllable on [0, T].

Example 4.1 We consider the following abstract fuzzy differential equations in credibility space where the state x_t takes values in X(⊂ E_N) and another bounded space Y (⊂ E_N). E_N is the set of all upper semicontinuously convex fuzzy numbers on R, (,,C_r) is credibility space, A is a fuzzy coefficient, the state function x : [0, T]×(,,C_r) → X is a fuzzy process, f : [0, T]×X → X is a regular fuzzy function, u : [0, T] × (,,C_r) → Y is a control function, B is a linear bounded operator from Y to X. C_t is a standard Liu process, x₀ ∈ E_N is an initial value.

Let f(t, x_t) =tx_t, , defining z_t = S ⁻¹(t)x_t, then the balance equations become

Therefore Lemma 3.2 is satisfy.

The α-level set of fuzzy number is [2]^α = [α + 1, 3 − α] for all α ∈ [0, 1]. Then α-level sets of f(t, x_t) is [f(t, x_t)]^α = Further, we have where m = 3T satisfies the inequality in hypothesis (H1), (H2). Then all the conditions stated in Theorem 3.1 are satisfied.

Let an initial value x₀ is . Target set is x¹ = The α-level set of fuzzy number is [] = [α − 1, 1 − α], α ∈ (0, 1]. We introduce the α-level set of us of Eq. (4). Then substituting this expression into the Eq. (5) yields α-level of x_T . Then all the conditions stated in Theorem 4.1 are satisfied. So the Eq. (4) are controllable on [0, T].

If there is an exact controllability encouraged for the abstract fuzzy differential equations, it can provide a benchmark for an approach to handle controllability about the equations such as fuzzy semilinear integrodifferential equations, fuzzy delay integrodifferential equations on the credibility space. Therefore, the theoretical result of this study can be used to make stochastic extension on the credibility space.