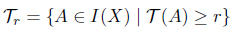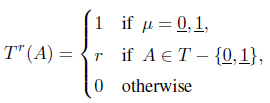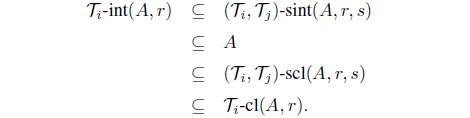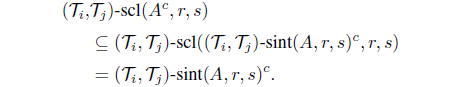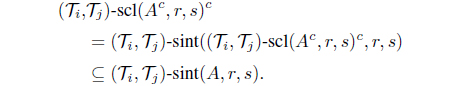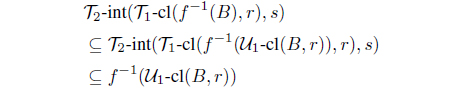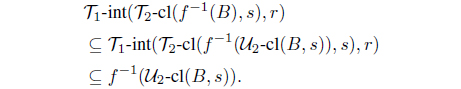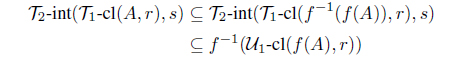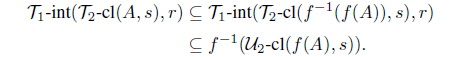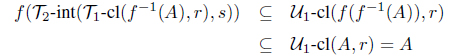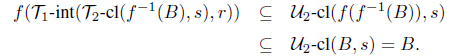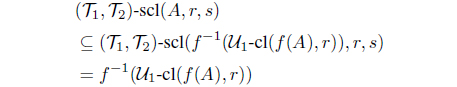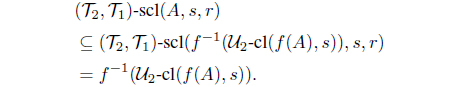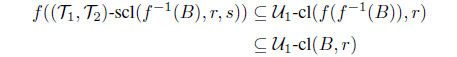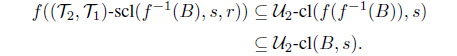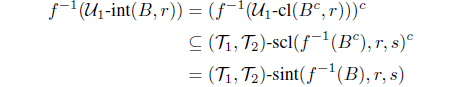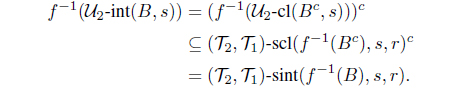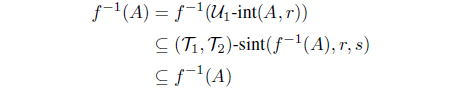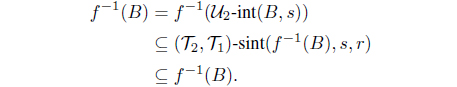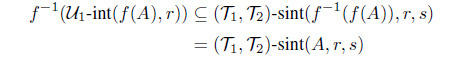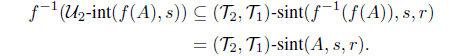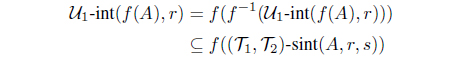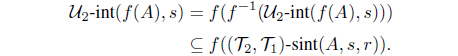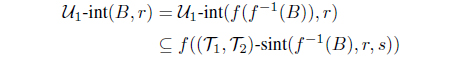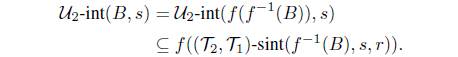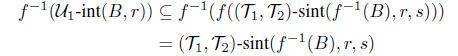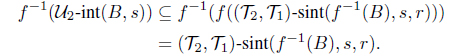Chang [1] introduced the notion of fuzzy topology. Chang’s fuzzy topology is a crisp subfamily of fuzzy sets. However, in his study, Chang did not consider the notion of openness of a fuzzy set, which seems to be a drawback in the process of fuzzification of topological spaces. To overcome this drawback, Šostak [2, 3], based on the idea of degree of openness, introduced a new definition of fuzzy topology as an extension of Chang’s fuzzy topology. This generalization of fuzzy topological spaces was later rephrased as smooth topology by Ramadan [4].

Çoker and his colleague [5, 6] introduced intuitionistic fuzzy topological spaces using intuitionistic fuzzy sets which were introduced by Atanassov [7]. Mondal and Samanta [8] introduced the concept of an intuitionistic gradation of openness as a generalization of a smooth topology.

On the other hand, Kandil [9] introduced the concept of fuzzy bitopological spaces as a natural generalization of Chang’s fuzzy topological spaces. Lee and his colleagues [10, 11] introduced the notion of smooth bitopological spaces as a generalization of smooth topological spaces and Kandil’s fuzzy bitopological spaces.

Lim et al. [12] defined the term “intuitionistic smooth topology,” which is a slight modification of the intuitionistic gradation of openness of Mondal and Samanta, therefore, it is different from ours.

In this paper, we introduce intuitionistic smooth bitopological spaces and the notions of intuitionistic fuzzy (,)-(r, s)-semiinterior and semiclosure. Based on these concepts, the characterizations for the intuitionistic fuzzy pairwise (r, s)-semicontinuous mappings are obtained.

I denotes the unit interval [0, 1] of the real line and I₀ = (0, 1]. A member μ; of I^X is called a fuzzy set in X. For any μ ∈ I^X, μ^c denotes the complement 1-μ. By and we denote constant mappings on X with value of 0 and 1, respectively.

Let X be a nonempty set. An intuitionistic fuzzy set A is an ordered pair A=(μA, γA) where the functions μ_A : X → I and γ_A : X → I denote the degree of membership and the degree of nonmembership, respectively, and μ_A + γ_A ≤ 1. Obviously, every fuzzy set μ in X is an intuitionistic fuzzy set of the form (μ,-μ). I(X) denotes a family of all intuitionistic fuzzy sets in X and “IF” stands for intuitionistic fuzzy.

Definition 1.1. ( [4]) A smooth topology on X is a mapping T : I^X → I which satisfies the following properties: (1) (2) (3) The pair (X, T) is called a smooth topological space.

Definition 1.2. ( [11]) A system (X, T₁, T₂) consisting of a set X with two smooth topologies T₁ and T₂ on X is called a smooth bitopological space.

Definition 1.3. ( [5]) An intuitionistic fuzzy topology on X is a family T of intuitionistic fuzzy sets in X which satisfies the following properties: (1) (2) If , then (3) If for each i, then The pair (X, T) is called an intuitionistic fuzzy topological space.

Now, we define the notions of intuitionistic smooth topological spaces and intuitionistic smooth bitopological spaces.

Definition 2.1. An intuitionistic smooth topology on X is a mapping : I(X) → I which satisfies the following properties:

(1)(0)=(1)=1.(2) (3)

The pair (X, T ) is called an intuitionistic smooth topological space.

Let (X, T ) be an intuitionistic smooth topological space. For each , an r-cut

is an intuitionistic fuzzy topology on X.

Let (X, T) be an intuitionistic fuzzy topological space and Then the mapping T^r : I(X) → I defined by

becomes an intuitionistic smooth topology on X.

Definition 2.2. Let A be an intuitionistic fuzzy set in intuitionistic smooth topological space (X, T ) and Then A is said to be

(1)IF - r -open if (2)IF - r -closed if

Definition 2.3. Let (X, T ) be an intuitionistic smooth topological space. For and for each A ∈ I(X), the IF -r-interior is defined by

and the IF -r-closure is defined by

Theorem 2.4. Let A be an intuitionistic fuzzy set in an intuitionistic smooth topological space (X, T ) and Then

(1)-int(A, r)c=-cl(Ac, r). (2)-cl(A, r)c=-int(Ac, r).

Proof. It follows from Lemma 2.5 in [13].

Definition 2.5. A system (X, , ) consisting of a set X with two intuitionistic smooth topologies and on X is called a intuitionistic smooth bitopological space(ISBTS for short). Throughout this paper the indices i, j take the value in {1, 2} and i ≠ j.

Definition 2.6. Let A be an intuitionistic fuzzy set in an ISBTS (X, , ) and r, s∈ I₀. Then A is said to be

(1) an IF (,)-(r, s)-semiopen set if there exist an IF --open set B in X such that B ⊆ A⊆ -cl(B, s), (2) an IF (,)-(r, s)-semiopen set if there exist an IF --closed set B in X such that -int(B,s)⊆A⊆B

Theorem 2.7. Let A be an intuitionistic fuzzy set in an ISBTS (X, , ) and r, s∈ I₀. Then the following statements are equivalent:

(1) A is an IF (, )-(r, s)-semiopen set. (2) Ac is an IF (, )-(r, s)-semiclosed set. (3) -cl(-int(A, r), s) ⊇ A. (4) -int(-cl(Ac, r), s) ⊆ Ac.

Proof. (1) ⇒ (2) Let A be an (, )-(r, s)-semiopen set. Then there is an IF -r-open set B in X such that B ⊆ A ⊆ -cl(B, s). Thus -int(B^c, s) ⊆ A^c ⊆ B^c. Since B^c is IF -r-closed in X, A^c is a IF (, ) -(r, s)-semiclosed set in X.

(2) ⇒ (1) Let A^c be an IF (, )-(r, s)-semiclosed set. Then there is an IF -r-closed set B in X such that -int(B, s) ⊆ A^c ⊆ B. Hence B^c ⊆ A ⊆ -cl(B^c, s). Because B^c is IF -r-open in X, A is an IF (, )-(r, s)-semiopen set in X.

(1) ⇒ (3) Let A be an IF , )-(r, s)-semiopen set in X. Then there exist an IF -r-open set B in X such that B ⊆ A ⊆ -cl(B, s). Since B is IF -r-open, we have B = -int(B, r) ⊆ -int(A, r). Thus -cl(-int(A, r), s) ⊇ -cl(B, s) ⊇ A.

(3) ⇒ (1) Let -cl(-int(A, r), s) ⊇ A and take B = -int(A, r). Then B is an IF -r-open set and Hence A is an IF (, )-(r, s)-semiopen set.

(3) ⇔ (4) It follows from Theorem 2.4.

Theorem 2.8. Let A be an intuitionistic fuzzy set in an ISBTS (X, , ) and r, s∈ I₀. Then (1) If A is IF -r-open in (X, ), then A is an IF (, )- (r, s)-semiopen set in (X,, ). (2) If A is IF -s-open in (X, ), then A is an IF (, )- (s, r)-semiopen set in (X,, ).

Proof. (1) Let A be an IF -r-open set in (X, ). Then A = -int(A, r). Thus we have -cl(-int(A, r), s) = -cl(A, s) ⊇ A. Hence A is IF (, )-(r, s)-semiopen in (X, , ).

(2) Similar to (1).

The following example shows that the converses of the above theorem need not be true.

Example 2.9. Let X = {x, y} and let A₁, A₂, A₃, and A₄ be intuitionistic fuzzy sets in X defined as

A1(x) = (0.1, 0.7), A1(y) = (0.7, 0.2); A2(x) = (0.6, 0.2), A2(y) = (0.3, 0.6); A3(x) = (0.1, 0.7), A3(y) = (0.9, 0.1);

and

A4(x) = (0.7, 0.1), A4(y) = (0.3, 0.6). Define : I(X) → I and : I(X) → I byand Then (, ) is an ISBT on X. Note that and

Hence A₃ is IF (, )-( , )-semiopen and A₄ is IF (, )-(, )-semiopen in (X, , ). But A₃ is not an IF - -open set in (X, ) and A₄ is not an IF --open set in (X, ).

Theorem 2.10. Let (X,, ) be an ISBTS and r, s∈ I₀. Then the following statements are true:

(1) If {A_k} is a family of IF (, )-(r, s)-semiopen sets in X, then A_k is IF (, )-(r, s)-semiopen.

(2) If {A_k} is a family of IF (, )-(r, s)-semiclosed sets in X, then A_k is IF (, )-(r, s)-semiclosed.

Proof. (1) Let {A_k} be a collection of IF (, )-(r, s)-semiopen sets in X. Then for each k,Ak -cl(-int(Ak, r), s).So we haveThus A_k is IF (, )-(r, s)-semiopen.

(2) It follows from (1) using Theorem 2.7 .

Definition 2.11. Let (X; , ) be an ISBTS and r, s I₀. For each A I(X), the IF (, )-(r, s)-semiinterior is defined by

and the IF ((, )-(r, s)-semiclosure is defined by

Obviously, (, )-scl(A, r, s) is the smallest IF (, )-(r, s)-semiclosed set which contains A and (, )-scl(A, r, s)is the greatest IF (, )-(r, s)-semiopen set which is contained in A. Also, (, )-scl(A, r; s) = A for any IF (, )-(r, s)- semiclosed set A and (, )-scl(A, r, s)= A for any IF (, )-(r, s)-semiopen set A.

Moreover, we have

Also, we have the following results:

(1) (, )-scl(, ,r, s) = , (, )-scl(, r, s) = .

(2) (, )-scl(A, r, s) A.

(3) (, )-scl(A, r, s)∪ (, )-scl(B, r, s) (, ))-scl(A ∪ B, r, s).

(4) (, )-scl((, )-scl(A, r, s), r, s) = (, )-scl(A, r, s).

(5) (, )-sint(, r, s) = , (, )-sint(, r, s) = .

(6) (, )-sint(A, r, s) A.

(7) (, )-sint(A, r, s) ∩(, )-sint(B, r, s) (, )-sint(A ∩B, r, s).

(8) (, )-sint((, )-sint(A, r, s), r, s) = (, )-sint(A, r, s).

Theorem 2.12. Let A be an intuitionistic fuzzy set in an ISBTS (X, , ) and r, s I₀. Then we have

(1) (, )-sint(A, r, s)^c = (, )-scl(A^c, r, s).

(2) (, )-scl(A, r, s)^c = (, )-sint(A^c, r, s).

Proof. (1) Since

(, ) - sint(A, r, s) A and (, ) - sint(A, r, s)

is IF (, )-(r, s)-semiopen in X, A^c (, ) - sint(A, r, s)^c and (, ) - sint(A, r, s)^c is IF (, )-(r, s)-semiclosed. Thus

From that A^c (, )-scl(A^c, r, s) and (, )-scl(A^c, r, s) is IF (, )-(r, s)-semiclosed, (, )-scl(A^c, r, s)^c A and (, )-scl(A^c, r, s)^c is IF (, )-(r, s)-semiopen. Thus we have

Hence

(, ) - sint(A, r, s)^c (, ) - scl(A^c, r, s).

Therefore

(, ) - sint(A, r, s)^c = (, ) - scl(A^c, r, s).

(2) Similar to (1).

We define the notions of IF pairwise (r, s)-semicontinuous mappings in intuitionistic smooth bitopological spaces, and investigate their characteristic properties.

Definition 3.1. Let f : (X, ) → (Y, ) be a mapping from an intuitionistic smooth topological spaces X to an intuitionistic smooth topological spaces Y and Then f is called an IF r-continuous mapping if f^-1(B) is IF -r-open in X for each IF -r-open set B in Y .

Definition 3.2. Let f : (X,, ) → (Y, , ) be a mapping from an ISBTS X to an ISBTS Y and r, s I₀. Then f is said to be IF pairwise (r, s)-continuous if the induced mapping f : (X, ) → (Y, ) is an IF r-continuous mapping and the induced mapping f : (X, ) → (Y, ) is an IF s-continuous mapping.

Definition 3.3. Let f : (X,, ) → (Y, , ) be a mapping from an ISBTS X to an ISBTS Y and r, s I₀. Then f is said to be IF pairwise (r, s)-semicontinuous if f^-1(A) is an IF (, )-(r, s)-semiopen set in X for each IF -r-open set A in Y and f^-1(B) is an IF (, )-(s, r)-semiopen set in X for each IF -s-open set B in Y .

Remark 3.4. It is obvious that every IF pairwise (r, s)-continuous mapping is IF pairwise (r, s)-semicontinuous. But the following example shows that the converse need not be true.

Example 3.5. Let (X,, ) be an ISBTS as described in Example 2.9. Define : I(X) → I and : I(X) → I byand

Then (, ) is an ISBT on X. Consider a mapping f : (X,, ) → (Y, , ) defined by f(x) = x and f(y) = y.

Then f is IF pairwise (, )-semicontinuous. But f is not an IF pairwise (, )-continuous mapping.

Theorem 3.6. Let f : (X,, ) → (Y, , ) be a mapping from an ISBTS X to an ISBTS Y and r, s I₀. Then the following statements are equivalent:

(1) f is IF pairwise (r, s)-semicontinuous.

(2) f^-1(A) is an IF (, )-(r, s)-semiclosed set in X for each IF -r-closed set A in Y and f^-1(B) is an IF (, )-(s, r)-semiclosed set in X for each IF -s- closed set B in Y .

(3) For each intuitionistic fuzzy set B in Y ,

and

(4) For each intuitionistic fuzzy set A in X,

f(-int(-cl(A, r), s))-cl(f(A), r)

and

f(-int(-cl(A, s), r))-cl(f(A), s).

Proof. (1) (2) Trivial.

(2) (3) Let B be an intuitionistic fuzzy set in Y . Then -cl(B, r) is IF -r-closed and -cl(B, s) is IF -s-closed in Y . Hence by (2), f^-1(-cl(B, r)) is an IF (, )-(r, s)- semiclosed set and f^-1(-cl(B, s)) is an IF (, )-(s, r)- semiclosed set in X. Thus we obtain

and

(3) (4) Let A be an intuitionistic fuzzy set in X. Then by (3), we have

and

Hence

f(-int(-cl(A, r), s)) -cl(f(A), r)

and

f(-int(-cl(A, s), r)) -cl(f(A), s).

(4) (2) Let A be any IF -r-closed set and B any IF -s-closed set in Y . By (4), we obtain

and

Hence

and

Therefore f^-1(A) is an IF (, )-(r, s)-semiclosed set and f^-1(B) is an IF (, )-(s, r)-semiclosed set in X.

Theorem 3.7. Let f : (X,, ) → (Y, , ) be a mapping from an ISBTS X to an ISBTS Y and r, s I₀. Then the following statements are equivalent:

(1) f is IF pairwise (r, s)-semicontinuous.

(2) For each intuitionistic fuzzy set A in X,

f(, )-scl(A, r, s)) -cl(f(A), r)

and

f(, )-scl(A, s, r)) -cl(f(A), s)

(3) For each intuitionistic fuzzy set B in Y ,

(, )-scl(f^-1(B), r, s) f^-1(-cl(B, r))

and

(, )-scl(f^-1(B), s, r) f^-1(-cl(B, s)).

(4) For each intuitionistic fuzzy set B in Y ,

f^-1(-int(B, r)) (, )-sint(f^-1(B), r, s)

and

f^-1(-int(B, s)) (, )-sint(f^-1(B), s, r).

Proof. (1) (2) Let A be an intuitionistic fuzzy set in X. Then -cl(f(A), r) is IF -r-closed and -cl(f(A), s) is IF -s-closed in Y . Since f is IF pairwise (r, s)-semicontinuous, f^-1(-cl(f(A), r)) is an IF (, )-(r, s)-semiclosed set and f^-1(-cl(f(A), s)) is an IF (, )-(s, r)-semiclosed set in X. Hence

and

Therefore

f((, )-scl(A, r, s)) -cl(f(A), r)

and

f((, )-scl(A, s, r)) -cl(f(A), s)

(2) (3) Let B be an intuitionistic fuzzy set in Y . Then by (2), we obtain

and

Hence

(, )-scl(f^-1(B), r, s) f^-1(-cl(B, r))

and

(, )-scl(f^-1(B), s, r) f^-1(-cl(B, s)).

(3) (4) Let B be an intuitionistic fuzzy set in Y . Then by (3), we have

(, )-scl(f^-1(B^c), r, s) f^-1(-cl(B^c, r))

and

(, )-scl(f^-1(B^c), s, r) f^-1(-cl(B^c, s)).

Hence

and

(4) (1) Let A be any IF -r-open set and B any IF -s- open set in Y . Then -int(A, r) = A and -int(B, s) = B. Hence

and

Thus

f^-1(A) = (, )-sint(f^-1(A), r, s)

and

f^-1(B) = (, )-sint(f^-1(B), s, r).

Hence f^-1(A) is an IF (, )-(r, s)-semiopen set and f^-1(B) is an IF (, )-(s, r)-semiopen set in X. Therefore f is IF pairwise (r, s)-semicontinuous.

Theorem 3.8. Let f : (X,, ) → (Y, , ) be a bijective mapping from an ISBTS X to an ISBTS Y and r, s I₀. Then f is IF pairwise (r, s)-semicontinuous if and only if

and

for each intuitionistic fuzzy set A in X.

Proof. Let A be an intuitionistic fuzzy set in X. Since f is one-to-one, by Theorem 3.7, we have

and

Because f is onto, we obtain

and

Conversely, let B be an intuitionistic fuzzy set in Y . Since f is onto, we obtain

and

Because f is one-to-one, we have

and

Therefore by Theorem 3.7, f is an intuitionistic fuzzy pairwise (r, s)-semicontinuous mapping.

No potential conflict of interest relevant to this article was reported.