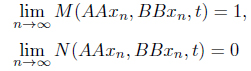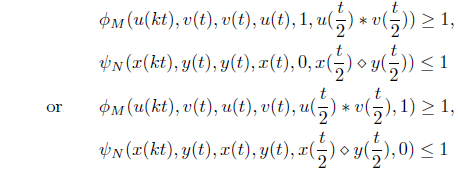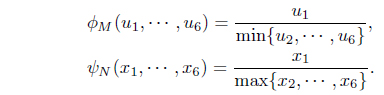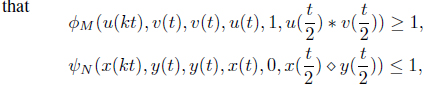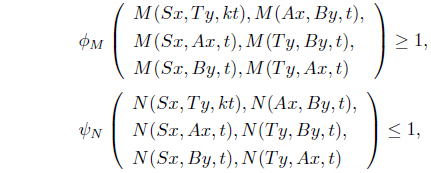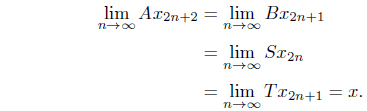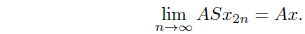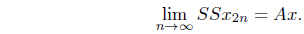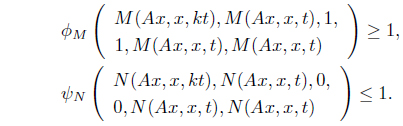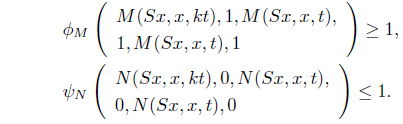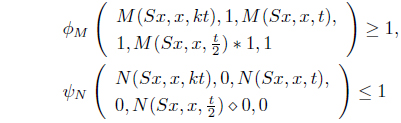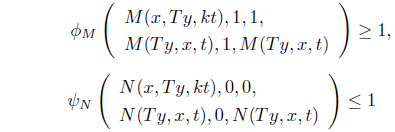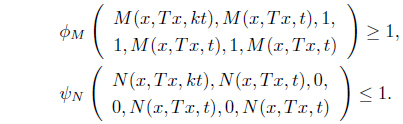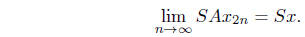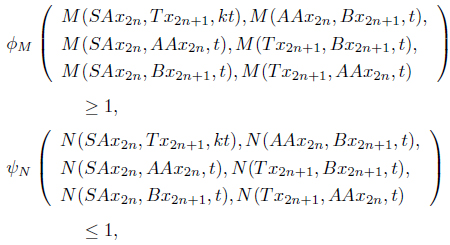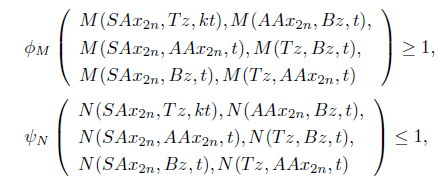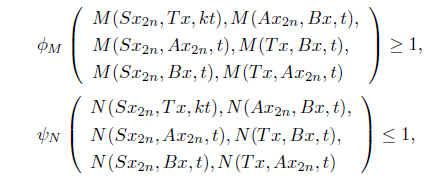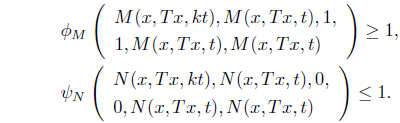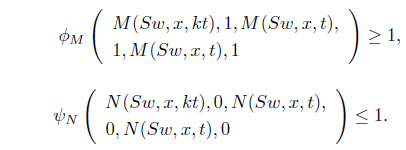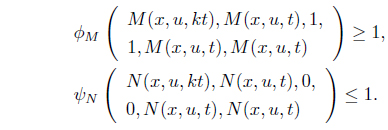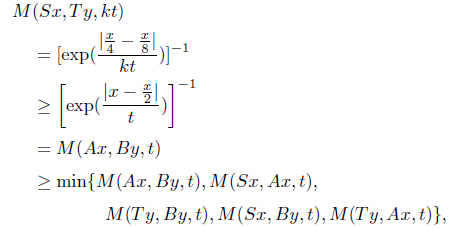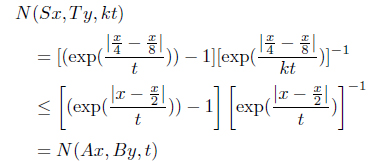In this paper, we establish common fixed point theorem for type(β) compatible four mappings with implicit relations defined on an intuitionistic fuzzy metric space. Also, we present the example of common fixed point satisfying the conditions of main theorem in an intuitionistic fuzzy metric space.
Zadeh [1] introduced the concept of fuzzy sets in 1965 and in the next decade, Grabiec [2] obtained the Banach contraction principle in setting of fuzzy metric spaces, Also, Altun and Turkoglu [3] proved some fixed theorems using implicit relations in fuzzy metric spaces. Furthermore, Park et al. [4] defined the intuitionistic fuzzy metric space, and Park et al. [5] proved a fixed point theorem of Banach for the contractive mapping of a complete intuitionistic fuzzy metric space. Recently, Park [6, 7], Park et al. [8] obtained a unique common fixed point theorem for type(𝛼) and type(𝛽) compatible mappings defined on intuitionistic fuzzy metric space. Also, authors proved the fixed point theorem using compatible properties in many articles [9–12].
In this paper, we will obtain a unique common fixed point theorem and example for this theorem under the type(𝛽) compatible four mappings with implicit relations defined on intuitionistic fuzzy metric space.
We will give some definitions, properties of the intuitionistic fuzzy metric space
Let us recall (see [13]) that a continuous
Similarly, a continuous
(a) is commutative and associative; (b) is continuous; (c) a 0 = a for all a ∈ [0, 1]; (d) a b ≥ c d whenever a ≤ c and b ≤ d (a, b, c, d ∈ [0, 1]).
Definition 2.1. ([14]) The 5..tuple (
(a) M(x,y,t) > 0, (b) M(x,y,t) = 1 x = y, (c) M(x,y,t) = M(y, x, t), (d) M(x,y,t) ⁎ M(y, z, s) ≤ M(x, z, t + s), (e) M(x,y,⋅) : (0,∞) → (0, 1] is continuous, (f) N(x,y,t) > 0, (g) N(x,y,t) = 0 x = y, (h) N(x,y,t) = N(y, x, t), (i) N(x,y,t) N(y, z, s) ≥ N(x, z, t + s), (j) N(x,y,⋅) : (0,∞) → (0, 1] is continuous.
Note that (
Definition 2.2. ([6]) Let
(a) {
M(xn, x, t) > 1 – 𝜖, N(xn, x, t) < 𝜖
for all
(b) {
M(xn, xm, t) > 1 – 𝜖, N(xn, xm, t) < 𝜖
for all
(c)
Lemma 2.3. ([8]) Let
M(x, y, kt) ≥ M(x, y, t), N(x, y, kt) ≤ N(x, y, t),
then
Definition 2.4. ([7]) Let
whenever {
Proposition 2.5. ([15]) Let
(a) BBxn → Ax if A is continuous at x, (b) AAxn → Bx if B is continuous at x, (c) ABx = BAx and Ax = Bx if A and B are continuous at x.
Implicit relations on fuzzy metric spaces have been used in many articles ([3, 16]). Let = {
(I)
(II) If, for some
for any fixed
u(ht) ≥ v(t) ⁎ u(t), x(ht) ≤ y(t) x(t).
(III) If, for some
ϕM(u(kt), u(t), 1, 1, u(t), u(t)) ≥ 1
for any fixed
𝜓N(x(kt), x(t), 0, 0, x(t), x(t)) ≤ 1
for any fixed
Example 2.6. ([6]) Let
Also, let
then from Park [6],
Now, we will prove some common fixed point theorem for four mappings on complete IFMS as follows:
Theorem 3.1. Let
(a) S(X) ⊆ B(X) and T(X) ⊆ A(X), (b) One of the mappings A, B, S, T is continuous, (c) A and S as well as B and T are type(𝛽) compatible (d) There exist k ∈ (0, 1) and ϕM, 𝜓N ∈ such that
for all x, y ∈ X and t > 0.
Then
Proof. Let
Now, let
By Proposition 2.5,
Using condition (d), we have, for any
and by letting
Therefore, by (III), we have
Hence
and, let
On the other hand, since
which implies that
which implies that
From (III), we have
Therefore, we have
Now, suppose that
By Proposition 2.5,
Using (d), we have for any
and by
Thus, we have, from (III),
Hence
letting
which implies that
letting
Thus,
Hence we have
x = Sx = SSw = AAw = Ax.
Hence
Finally, suppose that
Therefore, from (III),
Example 3.2. Let
a ⁎ b = min{a, b}, a b = max{a, b}
for all
Let
Thus the condition (d) of Theorem 3.1 is satisfied. Also, it is obvious that the other conditions of the theorem are satisfied. Therefore 0 is the unique common fixed point of
Park et al. [4, 5] defined an IFMS and proved uniquely existence fixed point for the mappings satisfying some properties in an IFMS. Also, Park et al. [8] studied the type(𝛼) compatible mapping, and Park [7] proved some properties of type(𝛽) compatibility in an IFMS.
In this paper, we obtain a unique common fixed point and example for type(𝛽) compatible mappings under implicit relations in an IFMS. This paper attempted to develop a proof method according to some conditions based on the fundamental properties and results in this space. I think that this results will be extended and applied to the other spaces, and further research should be conducted to determine how to combine the collaborative learning algorithm with our proof method in the future.
No potential conflict of interest relevant to this article was reported.