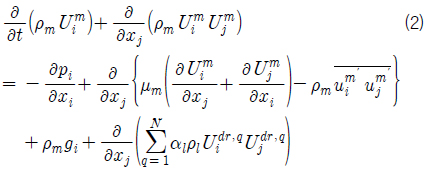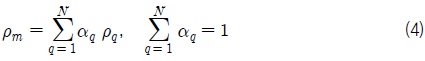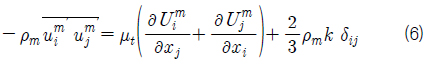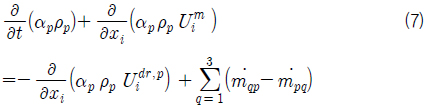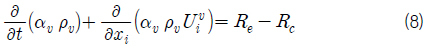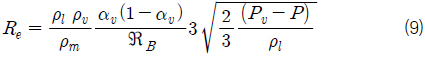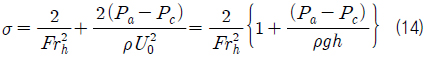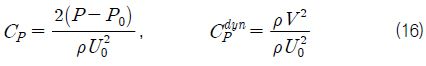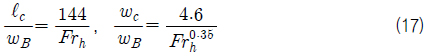The effects of the gravity field and the free surface on the cavity shape and the drag are investigated through a numerical analysis for the steady supercavitating flow past a simple two-dimensional body underneath the free surface. The continuity and the RANS equations are numerically solved for an incompressible fluid using a
최근 들어, 통상적인 운항 속도의 한계를 극복하고 수중에서 고속으로 운항이 가능하도록 하는 기술이 러시아, 미국, 독일 등 국방기술 선진국을 중심으로 연구·개발되고 있으며, 그 대표적인 예로 초월공동 또는 초공동(supercavitation)을 이용하는 어뢰 기술을 들 수 있다. 초공동 어뢰는 수중로켓에 의해 추진되며 머리에 장착된 캐비테이터(cavitator)에서 의도적으로 초공동을 발생시켜 몸통 전체를 감싸서 어뢰 표면이 물과 접촉하는 면적을 줄이고, 표면 압력분포를 변화시킴으로써 전체 항력을 낮추어 매우 빠른 속도로 운항할 수 있다. 이미 개발되어 배치된 것으로 알려진 초공동 어뢰로는 러시아의 Shkval과 이를 개조한 이란의 Hoot가 있고, 연구·개발 중인 것으로는 독일의 Barracuda와 미국의 Supercav가 있다(Kim & Nah, 2011). 이들 초공동 어뢰는 수중에서 200노트 이상으로 운항이 가능한 것으로 알려져, 일반 어뢰의 주행속도가 40노트 전후임을 감안하면, 매우 빠른 속도임을 알 수 있다.
초공동을 발생시키는 핵심부인 캐비테이터는 초공동 어뢰의 머리에 장착되어 어뢰 몸통 전체를 감싸는 초공동을 발생시키는데, 자연 공동(natural cavity)이 발생하는 속도보다 낮은 속도에서 더 크고 안정된 초공동을 발생시키고 유지하기 위해 통상 캐비테이터 후방의 노즐을 통해 고압가스를 분사시키는 환기 공동(ventilated cavity) 발생 방식을 사용하며, Fig. 1과 같이 Shkval은 원판(disk) 형상, Barracuda는 원뿔(cone) 형상의 캐비테이터를 채택하고 있다. 초공동 발생장치인 캐비테이터의 초공동 발생 및 항력 특성을 파악하고 성능을 평가하는 것은 초공동 어뢰의 연구·개발에서 핵심이 되는 기술로서 일찍부터 관련 연구가 이루어져 왔고, 최근까지도 지속되고 있다. 초공동 모델링에 대한 Riabouchinsky (1919)의 선도적인 연구를 필두로, 1940년대에는 Fisher (1944), Reichardt (1946), Eisenberg and Pond (1948), Plesset and Shaffer (1948) 등 주로 축대칭 또는 2차원 물체의 초공동 유동에 대한 실험을 중심으로 연구가 이루어졌고, 1950년대에는 Birkhoff, et al. (1950; 1952), Anderson (1953), Armstrong (1954), Self and Ripken (1955), Waid (1957a; 1957b), Wu (1957), Silberman (1958) 등 실험 및 포텐셜 유동 해석을 통한 연구가 수행되어 상당한 성과를 거두었다. 1960, 70년대에는 Schot (1962), Street (1963), Tulin (1964), Wu and Wang (1964), Street (1965), Gadd & Grant (1965), Klose and Acosta (1965), Brennen (1969), Logvinovich (1969), Wu, et al. (1971), May (1975) 등, 기초 연구는 물론 응용 연구가 활성화되었다. 1980년대 이후 20세기 말까지는 Epshtein and Laptin (1980), Delannoy and Kueny (1990), Kirschner, et al. (1995), Singhal, et al. (1997), Hrubes, et al. (1998), Kirschner (1997), Savchenko, et al. (1998) 등, 컴퓨터를 활용한 초공동 유동의 수치해석 연구를 중심으로 발전을 이루었고, 특히 러시아는 초공동 어뢰에 관한 응용 연구를 통해 큰 성과를 거두었다. 최근에는 Savchenko (2000), Kunz, et al. (2000), Ventikos and Tzabiras (2000), Vlasenko (2000), Hrubes (2001), Kunz, et al. (2001), Savchenko (2001), Singhal, et al. (2002), Alynak, et al. (2004), Schaffar, et al. (2005), Wosnik and Milosevic (2005), Wu, et al. (2005), Peng, et al. (2006), Karimi, et al. (2008), Passandideh-Farda & Roohi (2008), Nesteruk (2008), Ahn, et al. (2010), Petitpas, et al. (2011), Rabiee, et al. (2011), Ahn, et al. (2012), Lee, et al. (2013) 등, 실험 및 CFD 해석 그리고 기초 및 응용의 다양한 연구가 수행되고 있으며, 미국과 러시아 뿐 아니라 독일, 이란, 중국 등, 여러나라에서 관련 연구가 진행되고 있다.
이와 같이 오랫동안 수많은 연구가 수행되었음에도 불구하고 앞서 언급한 연구는 거의 모두가 무한유체 영역의 초공동을 대상으로 한 것으로서 수면이나 중력에 의한 영향을 제대로 고려하지 않고 있다. 단지, 캐비테이션 수를 정의할 때 운용 수심의 정수압을 포함시켜 고려하고 무한 Froude 수 가정을 사용하거나, 중력을 고려하지 않고 수면의 경계 조건만을 근사적으로 고려한 경우가 대부분이다. 그러나 초공동 어뢰가 운용되는 환경 조건은 균일한 압력의 무한유체 영역이 아니다. 끊임없이 운동하며 대기와 접촉하는 해수면이 가까이 존재하고, 중력과 수심에 따라 선형적으로 증가하는 정수압이 작용하는 환경에서 고속으로 주행한다. 따라서 중력과 수면의 경계조건이 초공동에 미치는 효과에 대한 연구가 필요하며, 특히 초공동 어뢰가 수심 10
한편, 초공동 어뢰가 실제 주행하는 환경 조건을 제대로 고려하여 실험을 수행하는 것은 현실적으로 거의 불가능하다. 특히 초공동 어뢰는 해수면 아래에서 고속으로 주행하기 때문에 원하는 수준의 낮은 캐비테이션 수에서 실험하기가 힘들고, 중력과 잠김 깊이의 영향과 대기압이 작용하는 수면의 경계조건을 포함 시켜서 실험하기는 더더욱 어려운 실정이다.
CFD 기법과 컴퓨터의 발전과 함께 최근에는 캐비테이션 해석모델과 수치해석해의 정도 향상을 위한 노력으로 인해 선박의 프로펠러와 타 등에서 발생하는 캐비테이션 유동에 대한 해석도 어느 정도 가능하게 되었다. 이 같은 CFD 기술의 현 수준은 초공동 유동에 대한 수치해석을 통해 초공동 어뢰의 성능 추정과 형상 설계에 필요한 초공동 발생 및 유체력 정보의 취득이 가능함을 시사한다. 따라서 CFD 기술을 적용하여 수중운동체의 초공동 유동과 유체력 특성에 대한 수치해석을 수행하는 것은 의미 있고 시의 적절하다고 판단된다.
본 논문에서는 2차원 단순 형상의 물체를 대상으로 중력장을 고려하고 대기와 수면을 포함시켜 초공동 유동에 대한 수치해석을 수행함으로써 중력과 자유표면이 초공동의 발생 및 항력에 미치는 효과에 대하여 조사하였다.
수면 아래에서 고속으로 운동하는 물체의 초공동 유동에 대한 수치해석을 수행하기 위해서는 공기, 물, 수증기가 혼재된 유동에 대한 수치해석 방법이 필요하다. 본 연구에서는 혼합유체 모델을 이용하여 대기와 물의 경계인 수면과 물과 수증기의 경계인 공동표면을 유동해석 영역 내부에 포함시켜서 비정상 난류유동에 대한 수치해석을 실시하였다.
공기, 물, 수증기의 2상 3종 유체 유동에는 물과 공기 그리고 물과 수증기 사이의 2가지 계면이 존재할 수 있으며, 유체역학적 관점에서 이 두 계면은 모두 자유 표면으로 정의할 수 있다. 하지만 본 논문에서는 혼동을 피하기 위해 대기와 접촉하는 물의 계면을 ‘자유 표면(free surface)’으로, 수증기와 물의 계면은 ‘캐비티 표면(cavity surface)’으로 구별하였다. 본 연구에서는 수치해석을 통해 구한 혼합유체의 체적분율 분포로부터 공기와 물의 체적분율이 0.5인 면을 ‘자유 표면’으로, 수증기와 물의 체적분율이 0.5인 면을 ‘캐비티 표면’으로 정의하였음을 미리 밝혀둔다.
혼합유체 유동에 대한 지배방정식은 연속방정식과 운동량 방정식인 RANS (Reynolds averaged Navier-Stokes) 방정식이다. 자유수면 아래의 초공동 유동에 대한 수치해석을 위해 지배방정식에 혼합유체 모델(mixture fluid model)을 적용하면, 연속방정식과 RANS 방정식은 각각 식 (1), (2)와 같이 나타낼 수 있다.
위, 아래 첨자
앞에서
한편, 식 (2) 우변의 는 혼합유체 내에 존재하는 개별 유체(
본 연구에서는 Boussinesq 가정으로부터 식 (6)과 같이 Reynolds 응력을 가정하고, turbulent eddy viscosity
체적분율 방정식(volume fraction equation)으로부터 공기와 수증기의 체적분율을 구하고, 식 (4)를 사용하여 물의 체적분율을 구한다. 공기와 수증기에 대한 체적분율 방정식은 다음과 같다.
계산된 각 체적분율로부터 혼합 밀도, 혼합 점성, 혼합 속도를 결정하고 액체와 기체 사이 계면의 위치를 구한다.
또한 캐비테이션 해석을 위해서는 체적분율 방정식 뿐 아니라 증기에 대한 수송방정식도 함께 풀어야 한다.
본 논문에서는 Schnerr and Sauer 캐비테이션 모델 (Fluent Theory Guide, 2011)을 사용하였다. 캐비테이션 해석을 위한 증기 수송방정식은 식 (8)과 같고, 우변은 기화 압력에 대한 상대 압력에 따라서 기화(evaporation) 또는 응축(condensation)하는 상변화를 모델링한 소스(source) 항이다.
여기서 𝜐는 증기 상(vapor phase)을 나타내고,
기포 반지름 과 같이 표현되고, 기화와 응축에 대한 계수는 동일하며, 증기 기포의 크기는 증기의 체적분율을 사용해서 식 (8)의 증기 수송방정식으로부터 구한다.
선체 주위 유동의 해석에 많이 사용하고 있는 유한체적법(FVM) 기반의 상용코드인 FLUENT(ver. 13)를 사용하였다. 지배 방정식의 확산항은 2차 중심차분, 대류항은 QUICK(Quardratic Upwind Interpolation for Converctive Kinematics) 방법으로 이산화 하였고, 속도-압력 연성은 SIMPLEC(Semi Implicit Method for Pressure Linked Equation Consistent) 방법을 사용하였다.
캐비테이션이 발생하는 유동의 상사를 위한 기본 무차원수는 캐비테이션 수로서 식 (11)과 같이 정의할 수 있다.
이 식에서
캐비티 유동의 상사를 엄밀하게 만족시키려면 캐비테이션 수 이외에도 Froude 수, Reynolds 수, Weber 수가 동일해야 하지만(Savchenko, 2001), 이 3개의 무차원수가 캐비티 유동에 미치는 영향은 무시할 수 있을 만큼 작은 경우가 대부분이기 때문에, 캐비테이션 수는 캐비티 유동의 특성을 규정하는 가장 중요한, 종종 유일한 무차원수로 인식되고 있다.
식 (11)로부터 알 수 있듯이 속도
한편, 수면 아래 가까운 곳에서 운동하는 물체에서 발생하는 초공동에 대해서는 중력은 물론 대기와 물의 경계인 수면의 영향을 무시할 수 없으며, Froude 수는 초공동 유동의 특성을 규정하는 중요한 무차원수가 된다. Froude 수는 다음과 같이 정의할 수 있으며,
물체에 의해 발생하는 수면파와 이에 따른 유동의 교란은 Froude 수가 커지면 상대적으로 작아져서 Froude 수가 아주 큰 경우에는 근사하여 처리할 수 있다. 초공동 물체의 경우에는 물체와 초공동을 포함한 전체 길이로 정의한 Froude 수를 사용하는 것이 보다 합리적이겠지만, 초공동의 길이는 초공동 유동 문제의 해로부터 정해지므로, 편의상 식 (12)와 같이 물체의 특성 길이로 정의하여 사용하는 것이 보통이다. 따라서 물체에서 발생하는 초공동의 길이를 고려하지 않은 Froude 수를 사용하여 수면파 및 관련 유동을 해석하는데 주의가 요구된다. 한편, 원판 캐비테이터의 초공동 유동에서는 통상 캐비테이터의 직경을 사용하여 정의한 Froude 수가 20~30 보다 큰 경우에 중력의 효과를 무시할 수 있다고 알려져 있다 (Savchenko, 2001).
식 (11)에서 기준 압력
위에서
수면 아래에서 운동하는 물체에서 초공동(supercavity)이 발생 하는 경우로는 물체의 속도가 매우 빨라져서 물체 주위의 압력이 증기압보다 낮아지면서 자연 초공동(natural supercavity)이 형성 되는 경우와 공기 또는 불활성 가스를 주입함으로써 캐비티 압력이 기준 압력에 근접해서 환기 초공동(ventilated supercavity)이 형성되는 경우를 생각할 수 있으며, 본 연구에서는 수면 아래에서 발생하는 자연 초공동을 대상으로 고려한다.
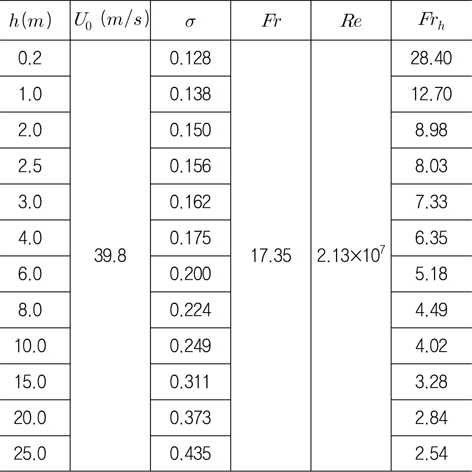
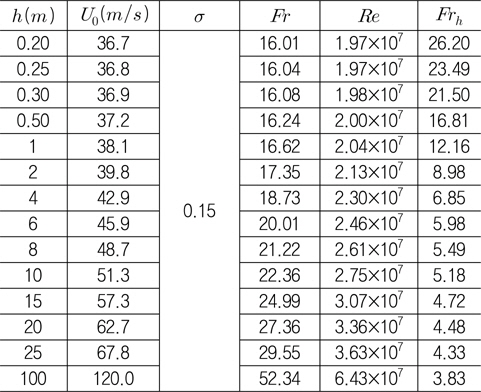
실제 수중 환경에서 발생하는 초공동 유동에서 캐비테이션 수를 변화시키는 주요 변수는 유입 속도와 잠김 깊이이다. 잠긴 깊이와 유입 속도가 달라지면 초공동 유동의 상사에 관계된 주요 무차원수인 캐비테이션 수(
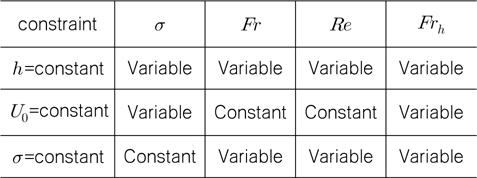
Table 1은 하나의 변수를 고정할 때 주요 무차원수의 변화 여부를 보여준다. 캐비테이션 수는 초공동 현상을 지배하는 가장 중요한 무차원수이지만 여기서는 초공동을 규정하는 변수로도 취급하였다. 잠김 깊이를 고정할 경우에는 유입 속도가 변하면 주요 무차원수가 모두 변하고, 유입 속도를 고정할 경우에는 잠김 깊이에 따라 캐비테이션 수와 잠김 깊이 Froude 수가 변한다. 또 캐비테이션 수가 동일하도록 잠김 깊이에 따라 유입 속도를 대응하여 변화시킬 경우에는 캐비테이션 수를 제외한 다른 무차원수가 함께 변한다. 한편, 어느 한 변수를 고정해도 잠김 깊이 Froude 수는 변한다.
[Table 1] Variation of dimensionless parameters

Variation of dimensionless parameters
캐비테이터의 기본 형상인 원판이나 원뿔에서 발생하는 초공동 유동은, 중력과 자유표면의 효과를 포함시키면, 축대칭성이 깨어져서 결과적으로 3차원 유동이 되므로, 본 연구에서는 우선 수치해석의 부담이 작은 웨지 각이 30°인 2차원 웨지를 대상으로 선택하여 중력과 자유표면 효과를 포함한 2차원 초공동 유동에 대한 수치해석을 수행하고, 그 결과를 무한유체 유동의 수치해(Lee, et al., 2013)와 비교, 분석하였다. 참고로 원뿔형 캐비테이터의 원추각(cone angle)이 통상 30° 정도인 것도 고려하였다.
2차원 초공동 유동에 미치는 중력과 자유표면의 효과를 체계적으로 조사하기 위해 Table 1과 같이 첫째로, 잠김 깊이를 고정하고 유입 속도를 변화시킨 경우, 둘째로, 유입 속도를 고정하고 잠김 깊이를 변화시킨 경우, 마지막으로 캐비테이션 수가 동일하도록 잠김 깊이에 따라 유입속도를 대응하여 변화시킨 경우에 대한 수치해석 결과를 순차적으로 조사, 검토하였다.
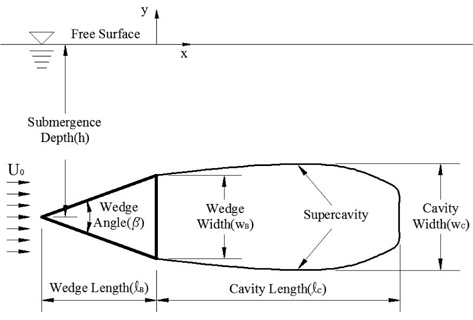
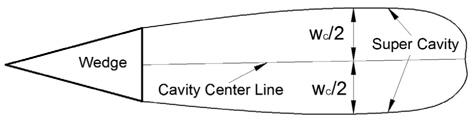
수치해석을 위한 좌표계와 초공동 형상의 정의를 Fig. 2에 나타내었다. 웨지 뒷날(trailing edge)로부터 수직 방향으로 정수면과 만나는 곳을 원점으로 잡고, 하류 방향을
3.2 잠김 깊이를 고정하고 유입 속도를 변화시킨 경우
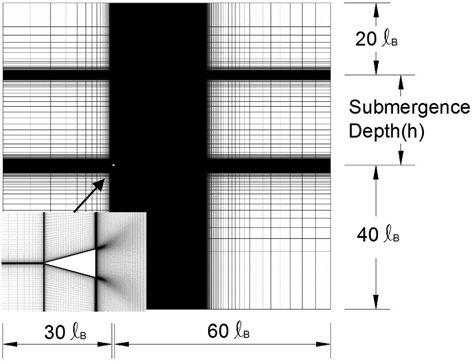
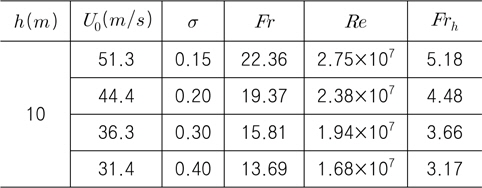
2차원 웨지에서 발생하는 초공동의 수치해석을 위해서 먼저 잠김 깊이를 10
[Table 2] Calculation conditions of cavity flow for 30° wedge under free surface (h=10m)
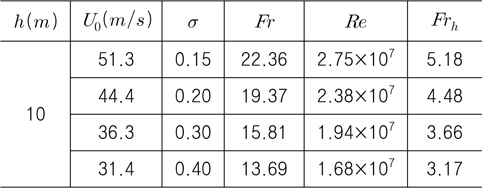
Calculation conditions of cavity flow for 30° wedge under free surface (h=10m)
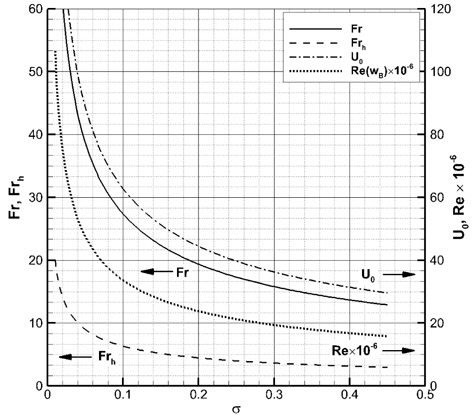
Fig. 4는 캐비테이션 수에 대응되는 유입 속도 및 다른 무차원 수의 변화를 보여준다. 유입 속도가 빨라짐에 따라 캐비테이션 수는 유입 속도의 제곱에 반비례하여 감소하고, Froude 수, Reynolds 수, 잠김 깊이 Froude 수는 모두 유입 속도에 선형적으로 비례하여 증가한다. 여기서, 캐비테이션 수가 작을수록 Froude 수와 잠김 깊이 Froude 수는 빠르게 증가하여 커지는 것을 주목할 필요가 있다.
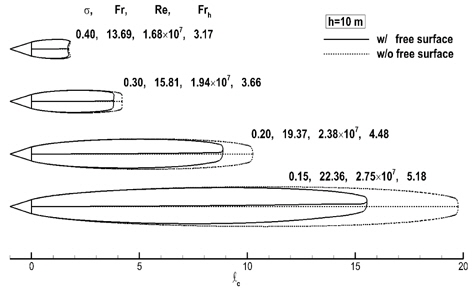
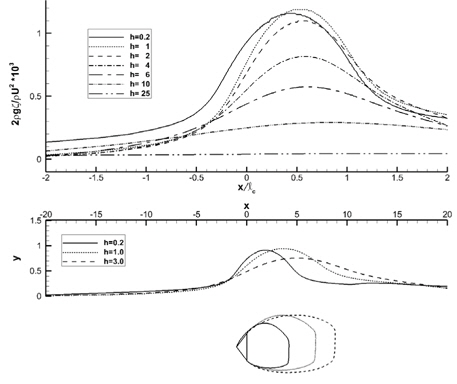
중력과 자유표면의 영향에서, 주로 부력에 의한 캐비티 형상의 변화를 나타내기 위해 동일한
Fig. 6은 캐비테이션 수에 따른 캐비티 형상의 변화를 보여준다. 중력과 자유표면을 포함시킨 경우와 무한유체 유동의 경우에 발생한 캐비티 형상을 비교하고, 각 캐비티 형상 옆에는 유동 조건에 해당되는 무차원수를 표시하였다. 두 경우의 캐비테이션 수와 Reynolds 수는 동일하고, Froude 수는 중력과 자유표면이 포함된 경우에만 해당된다.
두 경우 모두 캐비테이션 수가 작아질수록 캐비티는 빠르게 커진다. 캐비티가 가장 작은 경우(
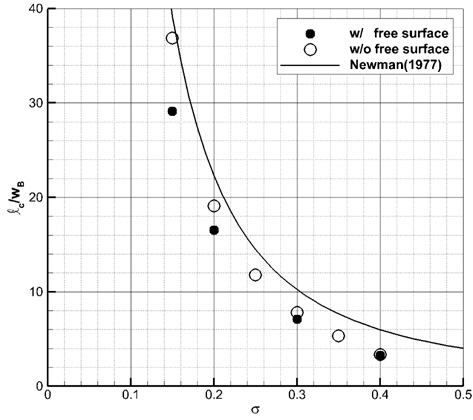
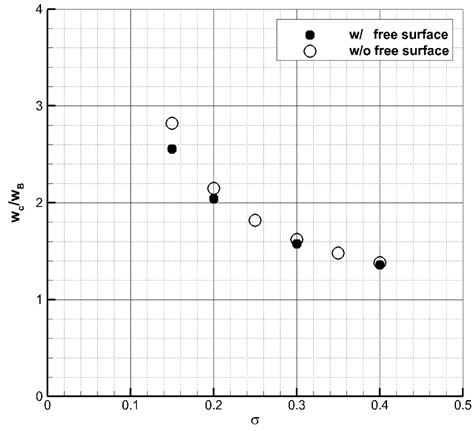
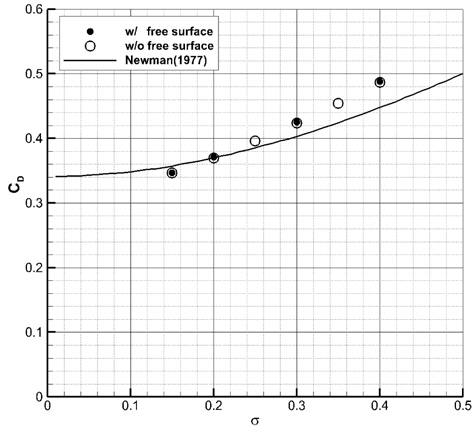
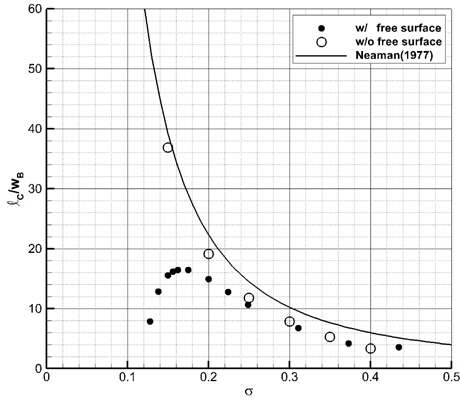
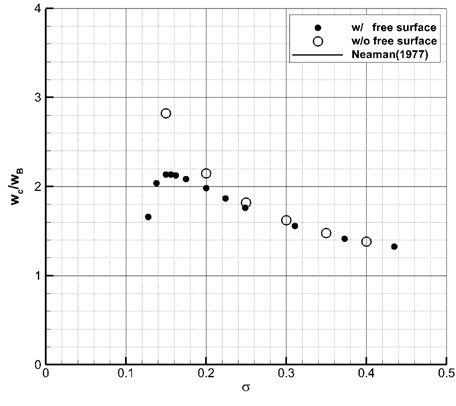
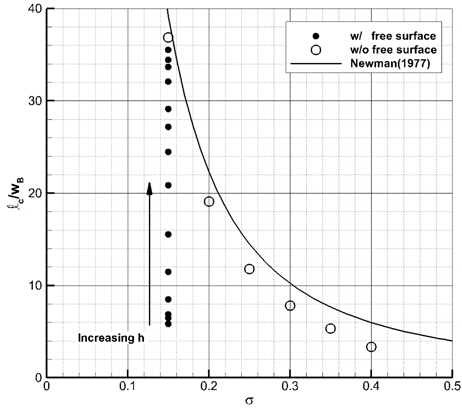
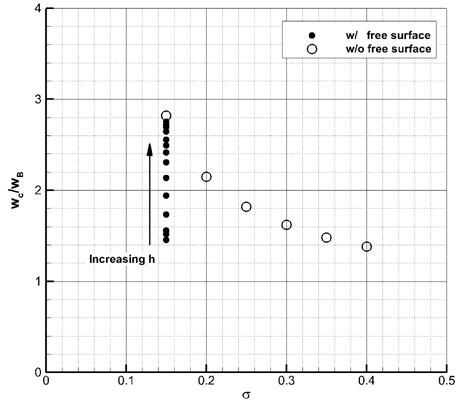
Fig. 7과 8에는 본 수치해의 캐비티 길이 및 두께를 무한유체 영역의 수치해 (Lee, et al., 2013) 및 선형이론해(Newman, 1977)와 비교하였다. 중력과 자유표면 효과 때문에 캐비테이션 수가 0.15일 때, 캐비티 길이는 20% 이상 줄어들고, 캐비티 두께는 10% 이내로 줄어든 것으로 나타났다. 캐비테이션 수가 작을수록 중력과 자유표면 효과로 인한 캐비티 길이와 폭의 감소율이 더 크다. 이 때, Froude 수는 증가하는 것을 고려하면, 캐비티 크기의 감소율이 더 커지는 본 연구의 결과는 Forude 수가 커질수록 중력과 자유표면의 효과가 상대적으로 작아진다는 통설과 맞지 않는다.
Fig. 9는 잠김 깊이가 10
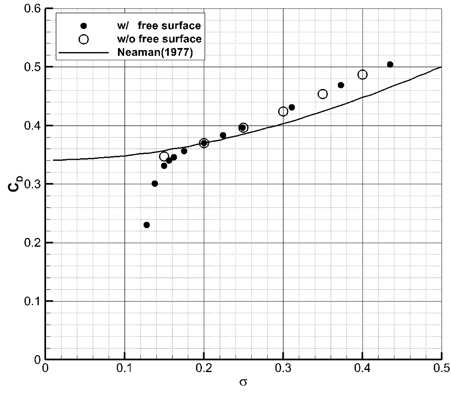
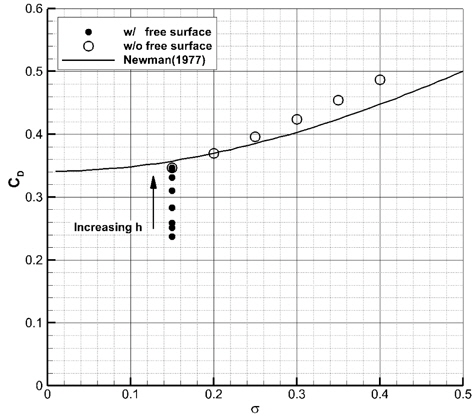
중력과 자유표면 효과 때문에 캐비티 크기가 눈에 띄게 줄어든 것과 달리, 항력 계수는 무한유체 유동의 경우보다 조금 크거나 차이가 거의 없어서 중력과 자유표면의 효과를 무시할 수 있음을 알 수 있다.
3.3 유입 속도를 고정하고 잠김 깊이를 변화시킨 경우
Froude 수가 일정한 조건에서 발생하는 초공동에 대해 조사하기 위해 잠김 깊이 2
Froude 수(
[Table 3] Calculation conditions of cavity flow for 30° wedge under free surface (U0=39.8m/s )
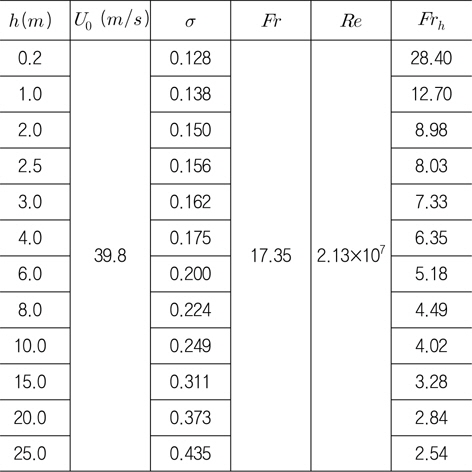
Calculation conditions of cavity flow for 30° wedge under free surface (U0=39.8m/s )
Fig. 10은 잠김 깊이에 대응되는 캐비테이션 수와 잠김 깊이 Froude 수의 변화를 보여준다. 식 (11)과 (12) 그리고 (13)으로 부터 알 수 있듯이 유입 속도를 고정한 본 경우에는 Froude 수가 일정하고, 잠김 깊이가 얕아짐에 따라서 기준 압력이 낮아져서 캐비테이션 수가 선형적으로 감소하며, 잠김 깊이 Froude 수는 잠김 깊이의 제곱근에 반비례해서 빠르게 증가한다.
Fig. 11은 잠김 깊이에 따라서 다르게 생성된 초공동 형상을 비교하여 보여주며, 각 잠김 깊이에 대응되는 캐비테이션 수와 잠김 깊이 Froude 수를 함께 표시하였다. 무한유체 유동의 경우에는 캐비테이션 수가 작아짐에 따라서 캐비티 길이와 두께가 빠르게 증가하는데, 유입 속도를 고정한 채 잠김 깊이를 변화시킨 본 경우에는 캐비테이션 수가 감소함에 따라서 캐비티의 길이와 두께가 증가하다가, 일정 깊이(3
Fig. 12와 Fig. 13을 살펴보면 중력과 자유표면의 효과 때문에 동일한 캐비테이션 수 조건에서 무한유체 유동의 경우에 비해서 캐비티 길이가 짧고 두께는 얇은 것을 알 수 있다. 잠김 깊이가 깊어짐에 따라서 캐비테이션 수가 증가하고 캐비티 크기는 무한 유체의 경우에 접근함을 확인할 수 있다. 잠김 깊이가 작아지면 캐비티 길이와 두께는 점점 더 커지고, 3.2절의 경우처럼 캐비테이션 수가 작을수록 캐비티 크기의 감소율이 더 크게 나타난다. 하지만 이 경우에는 3.2절과 달리 Froude 수가 고정되어 더 이상 중요한 변수가 아님을 주목할 필요가 있다.
잠김 깊이가 10
잠김 깊이가 3
이와 같이 수면에 아주 가까이 근접하게 되면 캐비테이션 수가 감소함에도 불구하고 중력과 자유표면 효과로 인해 초공동의 크기가 급격히 작아지는 ‘특이 양상’은 캐비테이터의 성능 추정 및 형상 설계에서 중요한 의미를 갖는다.
Fig. 14는 웨지의 항력 계수를 보여준다. 자유표면이 없는 경우와 거의 동일한 값과 유사한 변화를 나타내다가, 캐비티 크기의 경우와 마찬가지로 일정한 잠김 깊이(3
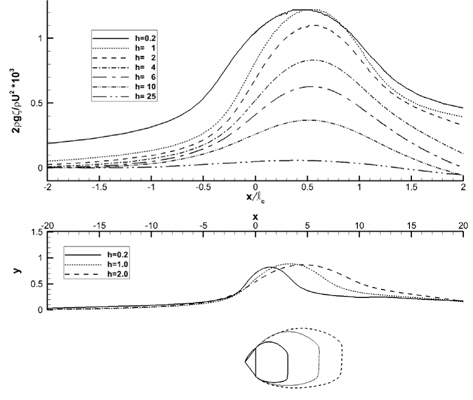
Fig. 15는 속도가 일정한 조건에서 잠김 깊이에 따른 자유수면의 변화를 보여준다. 잠김 깊이가 얕을수록 수면이 더 높이 상승 하다가 잠김 깊이가 1
3.4 캐비테이션 수를 고정하고 잠김 깊이를 변화시킨 경우
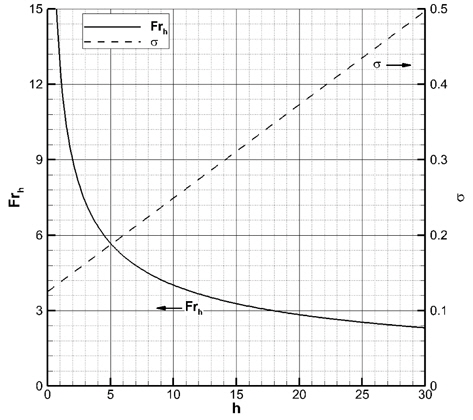
초공동 유동을 지배하는 가장 중요한 무차원수인 캐비테이션 수와 다른 무차원수의 영향을 분리하여 조사하기 위하여 0.2 ~ 100
[Table 4] Calculation conditions of cavity flow for 30° wedge under free surface (σ=0.15)
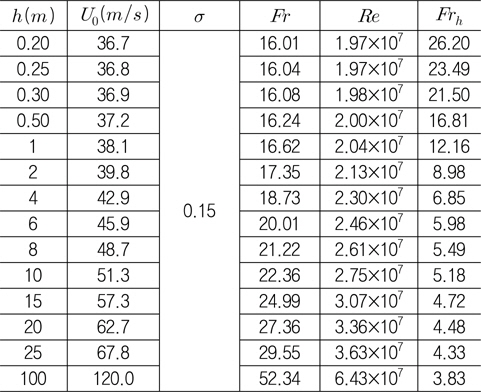
Calculation conditions of cavity flow for 30° wedge under free surface (σ=0.15)
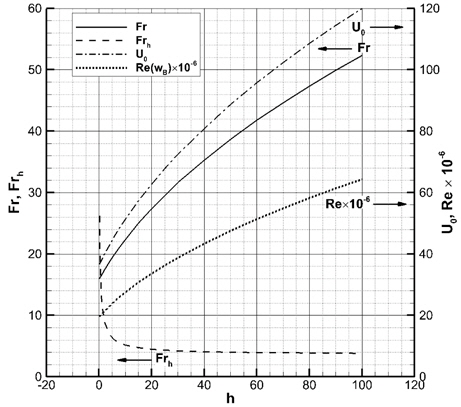
Fig. 16은 잠김 깊이에 대응되는 유입 속도 및 주요 무차원수의 변화를 보여준다. 초공동 웨지가 수면에 가까이 접근하여 잠김 깊이가 작을수록, 유입 속도, Froude 수, Reynolds 수가 더 빠르게 감소하고, 잠김 깊이 Froude 수는 잠김 깊이의 제곱근에 반비례하여 급격히 증가하는 것을 주목할 필요가 있다. 한편, 잠김 깊이가 깊어질수록 중력과 자유표면의 효과가 감소하여 초공동 유동이 무한유체 유동의 경우에 접근할 것이다.
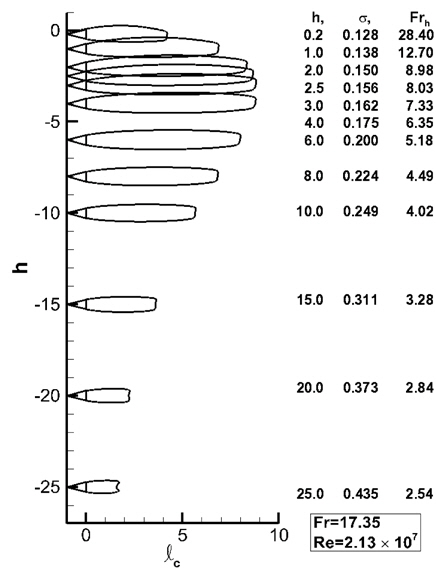
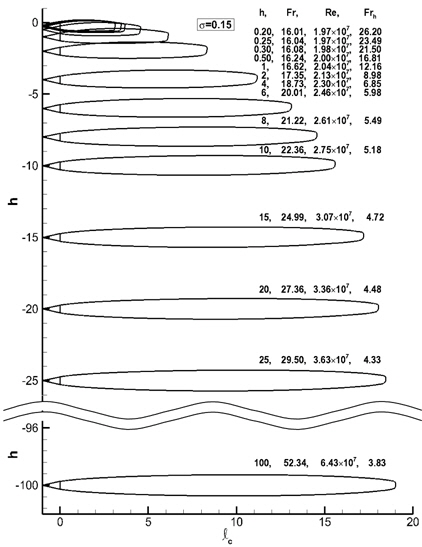
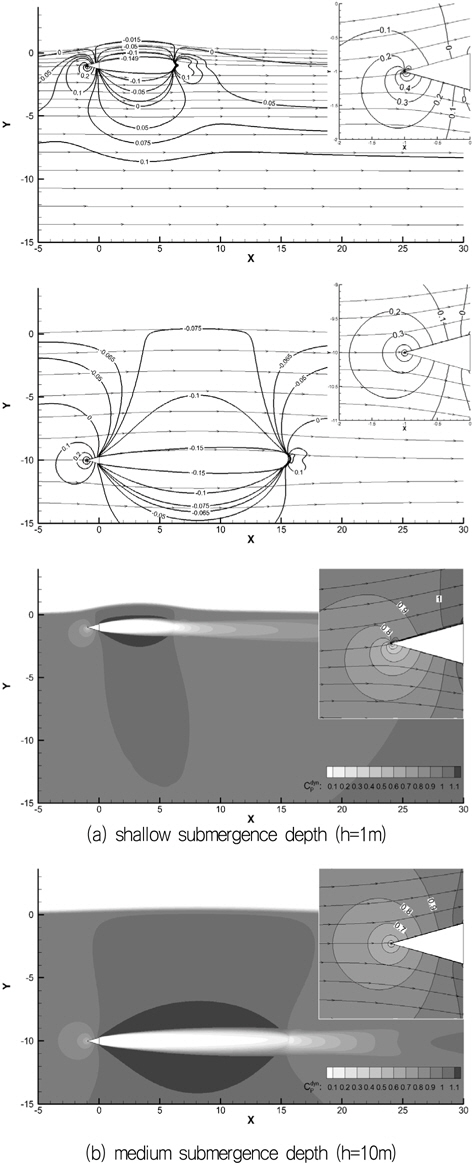
Fig. 17은 잠김 깊이 별로 생성된 초공동 형상을 비교하여 보여준다. 잠김 깊이가 20
Fig. 18과 19를 살펴보면 중력과 자유표면의 영향으로 동일한 캐비테이션 수 조건에서 캐비티 길이와 두께는 무한유체 유동의 경우 보다 모두 짧고 얇아지며, 잠김 깊이가 깊어짐에 따라서 캐비티 길이와 두께는 무한유체 유동의 값에 접근한다.
잠김 깊이 10
Fig. 20은 동일한 캐비테이션 수 조건에서 중력과 자유표면의 효과 때문에 잠김 깊이가 얕아짐에 따라서 웨지의 항력 계수가 감소하는 것을 보여준다. 잠김 깊이가 10
Fig. 21은 잠김 깊이 1
잠김 깊이에 따라 수면과 초공동 사이 유선의 곡률과 수직방향 압력구배의 차이가 크다. 잠김 깊이가 1
현재로서는 수면에 가까이 접근함에 따라서 캐비티 길이가 급격히 짧아지는 현상의 메커니즘과 원인을 정확히 설명하기 어렵지만, 대기압이 작용하는 수면과 증기압이 작용하는 초공동 캐비티 윗면 사이 아치형 유선의 곡률이 커지고 유선의 수직 방향으로 큰 압력구배가 작용하여 캐비티 닫힘을 촉진시키기 때문으로 판단된다. 이와 유사한 상황을 평판 초공동 유동에 대한 해석 결과 (Faltinsen & Semenov, 2008 의 Fig. 9)에서도 찾아 볼 수 있다.
Fig. 22는 수면 상승을 보여준다. 잠김 깊이에 따라 유입 속도가 크게 다름에도 불구하고 수면의 변화는 속도가 일정한 경우인 Fig. 15와 매우 유사하다. 특히 잠김 깊이가 얕은 경우, 캐비티 윗면의 유선 형상과 거의 동일하게 수면이 상승하여 아치형 유관을 형성한다.
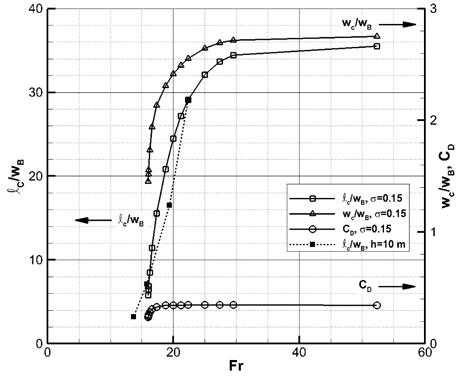
캐비테이션 수가 0.15로 고정된 조건에서 잠김 깊이에 따른 캐비티 길이와 두께 그리고 항력계수의 변화를 Froude 수를 변수로 하여 Fig. 23에 나타내었다. 또 잠김 깊이를 10
Froude 수가 대략 30 보다 커지면 캐비티 길이와 두께는 무한 유체 유동의 값에 점근하며, 항력계수는 Froude 수가 20 이상이면 무한유체 유동의 값과 동일하다. 이는 원판 캐비테이터의 초공동에서 Froude 수가 20 ~ 30 이상 일 경우, 중력의 효과를 무시할 수 있다는 통설 (Savchenko, 2001)과 어느 정도 맥락을 같이 한다.
Froude 수가 30보다 작아짐에 따라서 캐비티 길이와 두께는 빠르게 감소한다. 한편, 잠김 깊이를 10
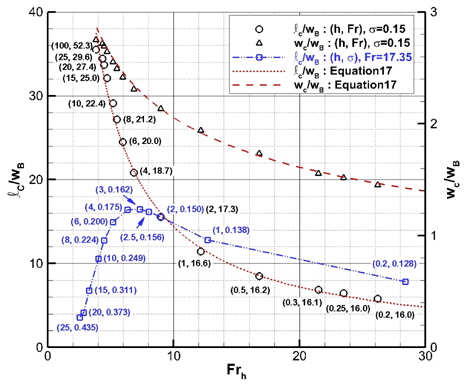
캐비테이션 수를 0.15로 고정시킨 경우의 캐비티 길이와 두께 그리고 Froude 수를 17.35로 고정시킨 경우의 캐비티 길이를 잠김 깊이 Froude 수를 변수로 하여 Fig. 24에 나타내었다. 수치해로부터 구한 캐비티 길이를 표시한 심볼 부근의 괄호 안 두 숫자는 전자의 경우, 잠김 깊이(
Froude 수가 고정된 경우의 캐비티 길이가 잠긴 깊이 Froude 수가 큰 영역에서 캐비테이션 수가 고정된 경우의 캐비티 길이와 유사한 경향으로 변하는 것으로부터, 수면에 가까이 근접하면 캐비티 길이가 잠긴 깊이 Froude 수에 의해서 지배되는 것을 알 수 있다. 또 잠김 깊이가 3
캐비테이션 수가 0.15로 고정된 경우의 결과는 캐비티 길이와 두께가 잠김 깊이 Froude 수에 역비례하여 줄어드는 것을 보여준다. 캐비티 길이와 두께를 잠김 깊이 Froude 수의 함수로 근사하여 Fig. 24에 표시하였으며, 근사식은 다음과 같다.
식 (17)은 웨지 각 30°인 2차원 웨지에 대해 캐비테이션 수가 0.15인 조건에서 도출된 근사식에 불과하지만, 더 큰 함의를 갖는다. 즉, 초공동 영역의 캐비테이션 수 조건에서 성립하는 식 (17)과 같은 근사식을 도출한다면, 캐비테이션 수만을 변수로 하는 경험식을 사용해서 추정한 무한유체 유동에 대한 초공동 캐비티의 길이와 두께로부터, 중력과 자유수면의 효과를 고려한 잠김 깊이에 따른 초공동 길이와 두께를 잠김 깊이 Froude 수만을 변수로 하는 근사식을 사용하여 추정할 수 있는 것이다.
수면 아래에서 발생하는 초공동 유동에 미치는 중력과 자유표면의 효과를 조사하기 위해 30° 웨지에서 발생하는 2차원 초공동 유동에 대한 수치해석을 수행하였다. 잠김 깊이와 유입 속도를 변화시켜 계산된 캐비티의 길이와 두께 그리고 웨지 항력을 무한 유체 유동의 결과와 비교함으로써 중력과 자유표면이 초공동 유동에 미치는 효과를 살펴보았으며, 그 결과는 다음과 같이 요약할 수 있다.
첫째, 중력과 자유표면의 효과 때문에, 동일한 캐비테이션 수 조건에서, 무한유체 유동의 경우에 비해 캐비티 길이는 짧아지고 두께는 얇아진다. 한편, 물체의 항력은 크게 달라지지 않는다.
둘째, Froude 수가 커질수록 중력과 자유표면의 효과는 감소하고, Froude 수가 어느 정도 이상 커지면 그 효과를 무시할 수 있으며, 결국에는 무한 Froude 수 또는 무한유체 유동의 경우로 점근한다.
셋째, 수면에 가까이 접근하여 잠김 깊이가 매우 얕아지면 캐비테이션 수가 감소함에도 불구하고 오히려 초공동 캐비티의 길이가 짧아지고 두께가 얇아지는 ‘특이 양상’이 나타난다.
마지막으로, 캐비테이션 수가 동일한 조건에서 초공동 캐비티의 길이는 잠김 깊이 Froude 수에 반비례하여 변한다.
본 연구를 통해 초공동 수중운동체가 수면 가까이에서 운용되는 경우에는 중력과 자유표면의 효과를 고려해야만 성능을 정확하게 추정할 수 있다는 것을 확인하였다. 향후, 원판 및 원뿔 캐비테이터 형상에 대한 후속 연구가 필요할 것으로 사료된다.