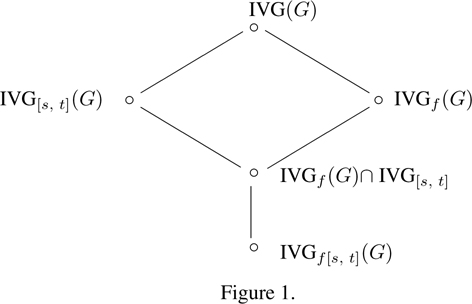
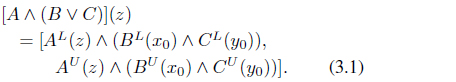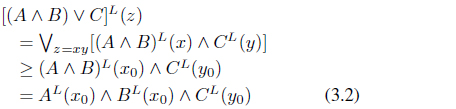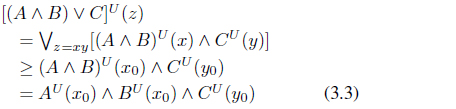We discuss some interesting sublattices of interval-valued fuzzy subgroups. In our main result, we consider the set of all interval-valued fuzzy normal subgroups with finite range that attain the same value at the identity element of the group. We then prove that this set forms a modular sublattice of the lattice of interval-valued fuzzy subgroups. In fact, this is an interval-valued fuzzy version of a well-known result from classical lattice theory. Finally, we employ a lattice diagram to exhibit the interrelationship among these sublattices.
In 1965, Zadeh [1] introduced the concept of a fuzzy set, and later generalized this to the notion of an interval-valued fuzzy set [2]. Since then, there has been tremendous interest in this subject because of the diverse range of applications, from engineering and computer science to social behavior studies. In particular, Gorzalczany [3] developed an inference method using interval-valued fuzzy sets.
In 1995, Biswas [4] studied interval-valued fuzzy subgroups. Subsequently, a number of researchers applied interval-valued fuzzy sets to algebra [5-11], and Lee et al. [12] furthered the investigation of interval-valued fuzzy subgroups in the sense of a lattice.
Later, in 1999, Mondal and Samanta [13] applied interval-valued fuzzy sets to topology, and Jun et al. [14] studied interval-valued fuzzy strong semi-openness and interval-valued fuzzy strong semicontinuity. Furthermore, Min [15-17] investigated interval-valued fuzzy almost M-continuity, the characterization of interval-valued fuzzy m-semicontinuity and intervalvalued fuzzy m
In this paper, we discuss some interesting sublattices of the lattice of interval-valued fuzzy subgroups of a group.
In the main result of our paper, we consider the set of all interval-valued fuzzy normal subgroups with finite range that attain the same value at the identity element of the group. We prove that this set forms a modular sublattice of the lattice of interval-valued fuzzy subgroups. In fact, this is an interval-valued fuzzy version of a well-known result from classical lattice theory. Finally, we use a lattice diagram to exhibit the interrelationship among these sublattices.
In this section, we list some basic concepts and well-known results which are needed in the later sections. Throughout this paper, we will denote the unit interval [0, 1] as
Let
Definition 2.1 [2,3]. A mapping
We will denote the set of all IVFSs in X as
Definition 2.2 [13]. Let
(i) A ⊂ B iff A L ≤ B L and A U ≤ B U. (ii) A = B iff A ⊂ B and B ⊂ A. (iii) A C = [1 − A U, 1 − A L]. (iv) A ∪ B = [A L ∨ B L , A U ∨ B U].(iv)' Aα = [ ,]. (v) A ∩ B = [A L ∧ B L, A U ∧ B U]. (v)' Aα = [,].
Result 2.A[13, Theorem 1]. Let
(a) ⊂ A ⊂ . (b) A ∪ B = B ∪ A , A ∩ B = B ∩ A. (c) A∪(B∪C) = (A∪B)∪C , A∩(B∩C) = (A∩B)∩C. (d) A, B ⊂ A ∪ B , A ∩ B ⊂ A, B. (e) A ∩ ( Aα) = ( A ∩ Aα). (f) A ∪ ( Aα ) = (A ∪ Aα). (g) () c = , () c = . (h) (A c) c = A. (i) (Aα) c = A cα , ( Aα) c = Acα.
Definition 2.3 [8]. Let (
Definition 2.4 [4]. Let
Result 2.A[8, Proposition 4.3]. Let
Result 2.B [4, Proposition 3.1]. Let
Result 2.C [8, Proposition 4.2]. Let
Definition 2.5 [8]. Let
3. Lattices of Interval-Valued Fuzzy Subgroups
In this section, we study the lattice structure of the set of intervalvalued fuzzy subgroups of a given group. From Definitions 2.1 and 2.2, we can see that for a set
Proposition 3.1. Let
Proof. Let {
Next we construct certain sublattice of the lattice IVG(
Definition 3.2[11]. Let (X, ·) be a groupoid and let
Lemma 3.3. Let
Proof. Let
The following is the converse of Lemma 3.2.
Lemma 3.4. Let
Proof. Let Then and Since Im
The following is the immediate result of Lemmas 3.3 and 3.4.
Proposition 3.5. Let
Definition 3.6 [8]. Let
We will denote the set of all IVNGs of
Result 3.A [6, Proposition 2.13]. Let
Result 3.B [6, Proposition 2.17]. Let
The following is the immediate result of Results 3.A and 3.B.
Theorem 3.7. Let
Result 3.C[8, Proposition 5.3]. Let
The following is the immediate result of Result 2.A and Definition 3.6.
Proposition 3.8. Let
It is well-known that the set of all normal subgroups of a group forms a sublattice of the lattice of its subgroups. As an interval-valued fuzzy analog of this classical result we obtain the following result.
Theorem 3.9. Let
Proof. Let
Let
Now let [
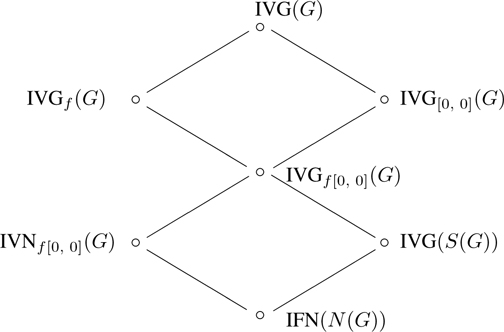
The relationship of different sublattice of the lattice of interval-valued fuzzy subgroup discussed herein can be visualized by the lattice diagram in Figure 1.
It is also well-known[20, Theorem I.11] that the sublattice of normal subgroups of a group is modular. As an interval-valued fuzzy version to the classical theoretic result, we prove that IVN([
Result 3.D [11, Lemma 3.2]. Let
Definition 3.10 [20,21]. A lattice (
In any lattice
Theorem 3.11. The lattice IVN
Proof. Let
On the other hand,
and
By (3.1), (3.2) and (3.3),
and
Then
and
Thus
and
So
and
By Result 2.B,
and
By Result 3.D,
Thus
This contradicts the fact that
We discuss some interesting facts concerning a special class of interval-valued fuzzy subgroups that attain the value [1, 1] at the identity element of
Lemma 3.12. Let A be a subset of a group
Proof. Let
The following can be easily seen.
Lemma 3.13. Let
Proposition 3.14. Let
Proof. Let
< [
Thus
[
Moreover, IVG(
Hence IVG(
Proposition 3.14 allows us to consider the lattice of subgroups
Now, in view of Theorems 3.9 and 3.11, for each fixed [
The lattice structure of these sublattices can be visualized by the diagram in Figure 2,
By using Lemmas 3.12 and 3.13, we obtain a well-known classical result.
Corollary 3.15. Let
Lee et al. [11] studied interval-valued fuzzy subgroup in the sense of a lattice. Cheong and Hur [5], Lee et al. [10], Jang et al. [6], Kang and Hur [8] investigated interval-valued fuzzy ideals/(generalized) bi-ideals, subgroup and ring, respectively.
In this paper, we mainly study sublattices of the lattice of interval-valued fuzzy subgroups of a group. In particular, we prove that the lattice IVNf[
In the future, we will investigate sublattices of the lattice of interval-valued fuzzy subrings of a ring.