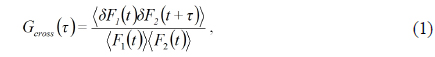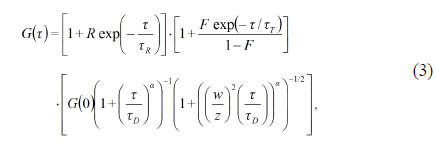Fluorescence correlation spectroscopy (FCS) was developed to study molecular diffusion dynamics and the photochemical properties of various fluorescent probes. FCS is based on the analysis of time-dependent fluorescence fluctuations from diffusing fluorescent probes. Since the late 1990s FCS has progressed due to advances in confocal systems and correlators, and due to the development of detectors with high quantum efficiency. It is well known that the diffusivity of a small particle in solution depends on the size of the particle and the viscosity of the solution. In most studies employing FCS, the relative size of the particle and viscosity of the sample solution have been determined using the Stokes-Einstein equation, based on the diffusion coefficient of a well-known probe in water [1-5]. These studies were unable to confirm particle shape, but the translational diffusion of fluorescent probes has often been investigated assuming that particles are spherical [6, 7].

The timescale of rotational diffusion for nanometer-sized probes introduces technical challenges, because the detectable time ranges of the correlator become expanded. However, photon antibunching and triplet formation occur on a timescale similar to that of rotational diffusion [8]. Fortunately, larger fluorescent probes (nanometer- or submicrometer-sized fluorescent particles such as quantum dots (Q-dots) and Q-rods) have different time scales for antibunching and lifetime, and they have no triplet state to complicate the analysis. Quantum particles are useful as probes due to their broad absorption bands, narrow emission bands, and high quantum yields [9, 10]. In particular, Q-rods of well-defined size and shape can be used as a standard to verify experimentally the diffusion properties of various rodlike molecules and particles.

In this study we built a simple confocal-microscope-based polarization FCS system using CW-laser excitation to investigate the rotational and translational diffusion of CdSe/CdS quantum rods. By autocorrelation analyses of various combinations of polarization and viscosity, we characterized the dependence of the rotational and translational diffusion of Q-rods on polarization by using the amplitude and characteristic time of the correlation function [11].

In a confocal microscope system, the movements of fluorescent particles into and out of the focal volume cause the detected fluorescence to vary in intensity, and this intensity variation inherently contains information about the size, number, shape, and speed of the particles. It is difficult to confirm a large number of total-time series data varying over less than a few milliseconds, so instead these data may be analyzed via the following correlation function:

where δF₁(t) is the fluctuation deviation in fluorescence intensity on one detector at time t, δF₂(t+τ) is the fluctuation deviation in fluorescence intensity on the other detector at time (t+τ), and <F₁(t)> and <F₂(t)> are the average fluorescence intensities of the time series signals at each detector. In general the correlation function obtained from experimental measurements shows several exponential decays, including those due to antibunching, triplet state, and translational and rotational diffusions [8]. The well-known correlation model equation includes three terms representing translational diffusion (G_D(τ)), triplet state (G_T(τ)), and rotational diffusion (G_R (τ)):

This equation can be expanded as follows:

where R is the rotational fraction, τ_R is the rotational diffusion time, F is the fraction of the triplet state, τ_T is the triplet state lifetime, G(0) is the initial amplitude of translational diffusion, and τ_D is the translational diffusion time. The terms τ_R, τ_T, and τ_D are characteristic times corresponding to the FWHM of each region. The beam waist w and axial length z are related to the form of the confocal volume [12].

The third term of Eq. (3) has been well established by various experiments showing that the parameters of the translational diffusion term carry quantitative information about the average particle number contained in the focal volume during τ_D, the diffusion coefficient, the hydrodynamic radius of the particles, and the viscosity of the solvent as determined by the Stokes-Einstein equation. The average particle number is simply the reciprocal of G(0). The second term indicating the triplet-state differs according to the presence or absence of each fluorophore. For fluorescent molecules such as rhodamine, this term varies according to background conditions [13], and this term is not present for semiconductors such as Q-dots. The first term shows a rotational diffusion; in the rotational diffusion, the rotational fraction R varies according to the polarization state of the FCS system [14,15]. In FCS the rotational diffusion coefficient D_R and translational diffusion coefficient D_T are often used to compare the dynamical properties of particles, given by Eq. (4) [16].

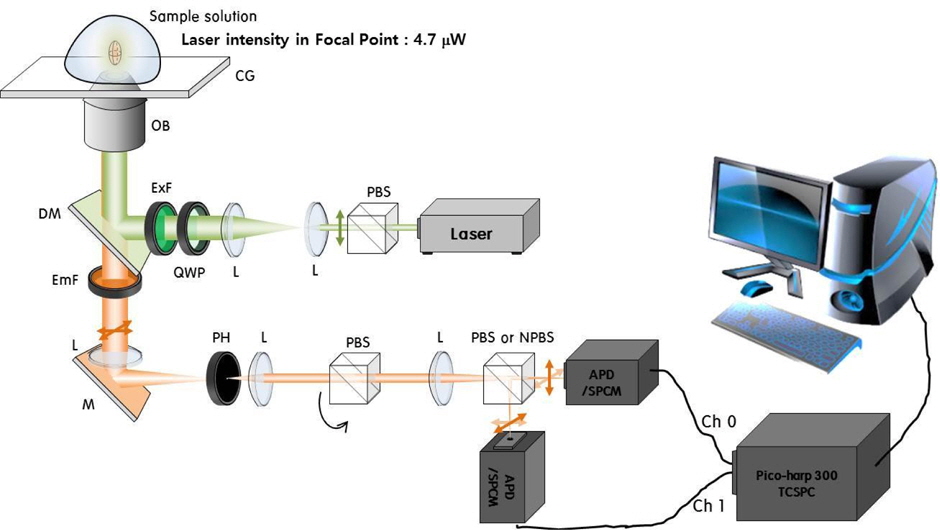
The FCS setup is illustrated schematically in Fig. 1. A 532-nm DPSS laser (Cobolt, Samba; 25 mW) and a single-photon counting module (SPCM; Id Quantique, id100-50) were used as the excitation source and detector respectively. Alignment of the optical components was accomplished using a commercial optical microscope (Olympus IX71). The optical components in the FCS setup were a polarization beam splitter (PBS), nonpolarized beam splitter (NPBS), excitation filter (ExF), dichroic mirror (DM), objective lens (OB), cover glass (CG), emission filter (EmF), lens (L), mirror (M), and pinhole (PH).

In this setup, the laser beam from the light source passes through the PBS and enters the optical microscope. The beam then passes through the ExF (Semrock, FF01-531/40-25) and reflects off the DM (Semrock, FF545/650-Di02). The reflected beam passes through the OB (Olympus, 60×, 1.2 NA), the immersion water, and the CG, and then focuses on a very small volume of a few fL inside the solution. The fluorescent particles in the focal volume are excited by the laser beam and then emit fluorescent light; a portion of this light enters the OB. After the light passes through the DM, EmF, and L, it escapes the microscope by the inner mirror. The light emerging from the microscope passes the PH, which is 30 μm in diameter, and the PBS. The PH and PBS are used to make a confocal conjugate point for the confocal volume, and to pass only the polarized fluorescence light, respectively. The light is split into two beams by the NPBS, and these beams are detected by two SPCMs. The fluorescent light detected at the SPCMs is converted into TTL signals, which are then converted into a correlation function by using a time-correlated single-photon counting system (PicoQuant, Picoharp300). The correlation function is monitored as the cross-correlation function of the responses of the two SPCSMs, using the FluoFit program (PicoQuant) [16], the delay time of the correlation being limited to the range from 0.15 μs to 0.1 s.

To investigate the rotational diffusion of rodlike particles, we used Q-rods (Q-rod591) of length 35 nm and width 5 nm (aspect ratio of 7) as the fluorescent particles. SEM analysis showed that the Q-rods were of uniform high quality, and TEM analysis showed that they were of uniform size (Fig. 2). The Q-rods were of a core/shell configuration, with CdSe cores and CdS shells. Q-rod growth is described in detail in Ref. [17]. The Q-rods had a maximum emission peak at 591 nm and could be sufficiently excited by the 532-nm laser beam.

To characterize the rotational diffusion of the Q-rod591 particles, we diluted them to a concentration of a few nM. At this concentration the number of Q-rods in the effective focal volume of our system would be less than 10. Therefore, we prepared samples of two different concentrations such that the average particle number in the focal volume would be approximately 4 (the “high-concentration” solution) or 0.5 (the “low-concentration” solution). In addition, Q-rod solutions with various viscosities were prepared, to study the dependence of rotational diffusion on viscosity, and to allow a comparison of that result to the effect of translational diffusion on viscosity. Glycerin was used to adjust the viscosity of the solutions with volume percentages of 0, 10, 20, 30, 40, and 50%; the corresponding viscosities of these solutions at 23 ℃ were 0.9, 1.2, 1.7, 2.6, 4.0, and 6.9 cP, as calculated using a formula for the viscosity of a glycerin-water mixture [18].

To examine the dependence of excitation and fluorescence on polarization states, two linear polarizers were used, one near the laser and one between the PH and the NPBS. The fluorescent light was split into two beams for cross correlation. The fluorescent light split by the NPBS was polarized into two states, XXX and XYY, in which the first letter X refers to the excitation light, and the last two letters denote the polarization states parallel to the excitation light (XX) and perpendicular to the light (YY), respectively.

Before analyzing the diffusion of Q-rods, we confirmed the effective focal volume of the FCS system based on polarization states using a rhodamine 6G (R6G) solution of about 10 nM concentration. At our laser intensity the correlation curve of the R6G solution revealed a triplet state and a translational diffusion state. Thus, the curve was fitted by Eq. (3) assuming the triplet state and linear translational diffusion (a=1). The fitting parameters was obtained via Eq. (3); for all polarization states the structure parameter s=z/w, triplet state time τ_T, and initial amplitude of translational diffusion G(0) were found to be 4.0±0.2, 1.4±0.22 μs, and 0.57±0.03 respectively, and the translational diffusion time τ_D was 43±4.7 μs for the XXX state and 43±5.0 μs for the XYY state. This result indicates that the effective focal volume (V_eff) of our FCS system does not depend on the polarization state. The beam waist was calculated to be 0.266 μm by Eq. (4), using the translational diffusion coefficient of R6G [19]. V_eff was calculated from this result, using the equation V_eff = π^3/2 w² z, yielding a value of 0.42 fL [1]. Additionally, to verify the performance of our FCS system we calculated the concentration of the R6G solution used in the measurements. The calculated concentration was 6 nM, which agreed fairly well with the expected value of 10 nM, with a difference of 4 nM; this indicated that the performance of the system was suitable to determine the concentration of the Q-rod solution. Therefore we determined the concentrations of both the low-concentration and high-concentration samples used in this study to be 2 and 16 nM respectively.

To investigate the polarization dependence of the rotational diffusion of Q-rods, we built the polarization FCS system and measured correlation functions of the Q-rods’ fluorescence responses. Measured functions were fitted by Eq. (3) to determine parameters related to the rotational and translational diffusion of the Q-rods. In Eq. (3) we neglected the triplet state because it does not appear in semiconductors such as Q-dots and Q-rods [19]. However, because the diffusion of Q-rods cannot be expected to be linear like that of Rhodamine 6G, due to the small differences in particle sizes and the irregular blinking in the full duration of the experiments, the anomalous diffusion exponent α was fitted by Eq. (3) using other parameters.

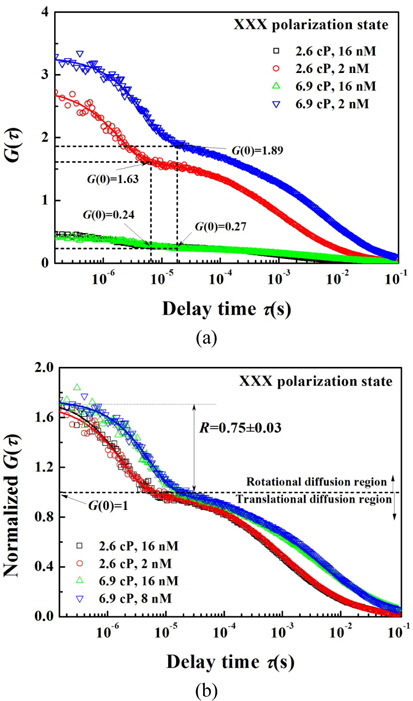
Before analyzing the influence of polarization, we examined the change in correlation function caused by varying the Q-rod concentration. Figure 3 shows the correlation functions obtained from Q-rod solutions of two different concentrations and the two solvent viscosities of 2.6 and 6.9 cP, in the XXX polarization state. The correlation functions varied greatly with viscosity and sample concentration (Fig. 3(a)). In samples of viscosity 2.6 cP, the amplitude of the correlation function G(τ) increased as the sample concentration decreased. This result was also observed in samples of viscosity 6.9 cP, indicating that G(τ) is inversely proportional to the concentration of the solution. In general, the initial value of the translational diffusion G(0) is proportional to the reciprocal of the number of particles in the effective focal volume. In the 2-nM samples, G(τ) increased as the viscosity of the sample was increased from 2.6 to 6.9 Q-rods’ fluorescence response, but the variation in G(τ) was less than the concentration variation. A similar result was also obtained for the 16-nM samples, but the increase in G(τ) with viscosity was very small compared to that for the 2 nM samples. This means that G(τ) depends more strongly on concentration than on viscosity. Although G(τ) showed a weaker dependence on viscosity than on concentration, the variation of G(τ) with viscosity cannot be neglected at the 2-nM concentration level.

As shown in Fig. 3(a), in samples of concentration 2 nM the G(0) values of the correlation functions for viscosities of 2.6 and 6.9 cP were 1.63 and 1.89 respectively. This result indicates that the effective focal volume was reduced as the viscosity of the solvent was increased. In both 2-nM samples the concentration of Q-rods was the same; therefore, the difference in viscosity was responsible for the variation in G(0). The samples of viscosity 6.9 cP used in this study included more glycerin than those of viscosity 2.6 cP; this increment of glycerin concentration increases the refractive index of the solution [20], thereby reducing the focal volume, and consequently decreasing the number of Q-rods passing through the reduced focal volume. This can be regarded as a reduction of the concentration of the solution.

According to the results in Fig. 3(a), the correlation functions obtained based on measurements of the Q-rod solutions were affected by the solutions’ concentration and viscosity. As mentioned previously, the goal in this study is to investigate the rotational diffusion of Q-rods in combination with their polarization states. To carry this out, the influences of the concentration and the viscosity in the translational diffusion of the correlation function were eliminated by using a normalized correlation function. The normalization was achieved by dividing G(τ) by G(0), which yielded the same normalized results for the two concentrations; the normalized functions differed only between the 2.6- and 6.9-cP viscosity groups (Fig. 3(b)). The function for the 6.9-cP group was time-delayed relative to that for the 2.6-cP group, but the normalized functions had the same amplitude in the rotational and translational diffusion regions, respectively. The functions were separated into regions corresponding to rotational and translational diffusion, described by two decay functions before and after approximately 10^-5 s. For translational diffusion the amplitude G(0) was 1, and the amplitude of rotational diffusion was 1.75±0.05. The difference of the amplitudes of rotational diffusion and translational diffusion is the rotational fraction; in this case, the rotational fraction was 0.75±0.05. This fraction has same value as the parameter R obtained by fitting. At a viscosity of 2.6 cP, the initial value of the function was lower than the rotational fraction. This means that the rotational region begins before 0.15 μs.

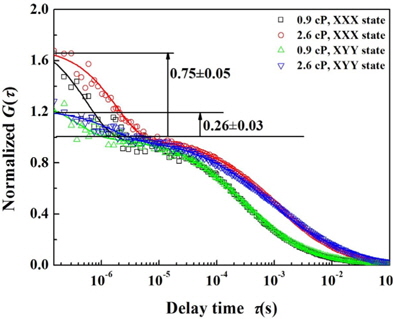
To analyze the rotational diffusion of Q-rods in combination with the polarization state, we measured and normalized the correlation function using viscosities of 0.9, 1.2, 1.73, 2.57, 4.06, and 6.9 cP and the polarization states XXX and XYY, and the normalized functions were fitted by Eq. (3) to obtain the parameters R, τ_R, τ_D, and α. For all polarization states the translational and rotational diffusion times increased as the viscosity increased. For the XXX state, the rotational diffusion time increased from 0.58±0.055 μs to 5.17±0.50 μs as the viscosity of the solvent increased from 0.9 to 6.9 cP; the diffusion time for the XYY state showed a similar trend, with the rotational diffusion time increasing from 0.42±0.074 μs to 3.27±0.22 μs as the viscosity increased in the same range. For the lowest viscosity of 0.9 cP, the diffusion times of the XXX and XYY states differed slightly, by 0.16 μs, but for the viscosity of 6.9 cP the difference was 1.90 μs. This result for the 6.9 cP viscosity may be due to nonlinear diffusion caused by irregular blinking and the small differences in size of the Q-rods in the high-viscosity solvent. Furthermore, the anomalous diffusion exponent α, quantifying the nonlinear diffusion of the Q-rods, decreases from 0.75 to 0.61 with increasing solvent viscosity [21]. This result also may indicate that the difference in diffusion times under high-viscosity conditions is due not to the polarization state but to nonlinear diffusion [22].

Figure 4 illustrates the normalized G(τ) for viscosities of 0.9 and 2.6 cP and the two polarization states studied; as shown in the figure, the rotational fractions were 0.75±0.05 in the XXX state and 0.26±0.03 in the XYY state. The fractions in the XYY state were smaller than those in the XXX state, which might an artifact of our FCS system. The system used in this study may be regarded as having three polarizers: a linear polarizer, a rotating linear polarizer, and an analyzer. The linear polarizer is in front of the light source, the rotating linear polarizer is the Q-rods in solution, and the linear analyzer is in front of the detector. The angle between the first polarizer and the last analyzer is 0° in the XXX state and 90° in the XYY state. The intensity of light passing through the three polarizers can be described by Malus’ law [23]: At 0° the maximum intensity ratio of input to output is 1, and at 90° the ratio is 0.25. According to this assumption the fraction for the XXX state would be 4 times as large as the value for the XYY state, but the observed difference was about 3 times as large, indicating that the Q-rods do not act as an ideal linear polarizer. If the Q-rods were rotating linear polarizers then the rotational diffusion time would also be expected to change with polarization state, but the rotational axis in Brownian rotation of the rod like particles is random at the full duration of the experiments.

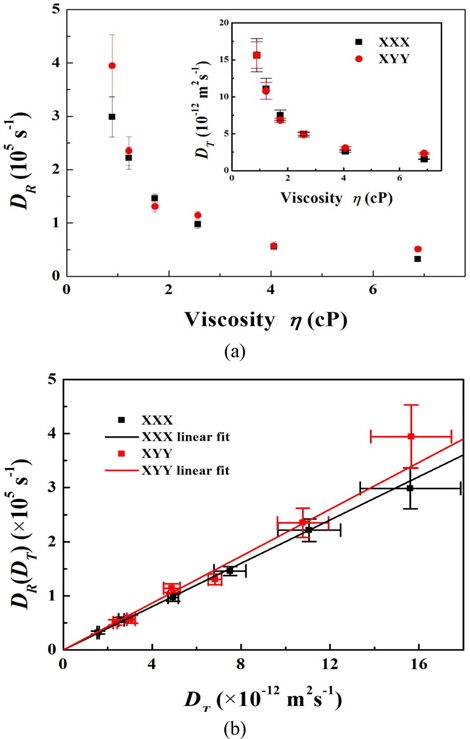
The rotational and translational diffusion coefficients were calculated by Eq. (4) using the diffusion time; the results are shown in Fig. 5(a) and Table 1. The results agree with the trend in diffusion time. As shown in Fig. 5a, the translational and rotational diffusion coefficients in 0.9-cP samples were (1.6±0.2)×10^-11 m² s^-1 and (2.9±0.4)×10⁵ s^-1 for the XXX state, and (1.5±0.2)×10^-11 m² s^-1 and (3.9±0.6)×10⁵ s^-1 for the XYY state, respectively.

The relationship between D_R and D_T was fairly linear in all polarization states (Fig. 5(b)); the linear-fit values of the slope D_R/D_T were 2.0×10¹⁶ m^-2 for the XXX state and 2.2×10¹⁶ m^-2 for the XYY state. According to previously published theories on the diffusion coefficient [22], D_R/D_T has a constant value determined by the particle’s aspect ratio and the square of the particle’s length. In the results herein, the linear fit with D_R=0 and D_T=0 gave a better result for the XXX state than for the XYY state.

We built a polarized fluorescence correlation spectroscopy system based on a confocal microscope, and measured and analyzed the correlation functions of CdSe/CdS Q-rods in solution for various concentrations and viscosities, and for two polarization states. In our analysis of the correlation functions with respect to polarization states, translational diffusion did not depend on the polarization state, whereas rotational diffusion depended strongly on polarization. The rotational fraction was 0.75±0.05 in the XXX state and 0.26±0.03 in the XYY state, and the rotational diffusion time in the XXX state was similar to that in the XYY state. We determined the diffusion coefficients based on the relation between the rotational and translational diffusion coefficients. The translational and rotational diffusion coefficients respectively ranged from 1.5×10^-11 m² s^-1 to 2.6×10^-12 m² s^-1 and from 2.9×10⁵ s^-1 to 5.6×10⁴ s^-1. Our results can be used to determine the size of rodlike particles, or to determine the rotational diffusion coefficients of particles of other sizes [25].