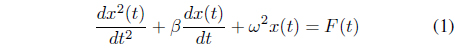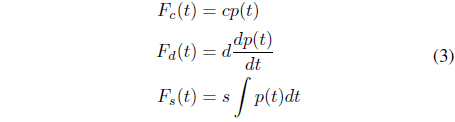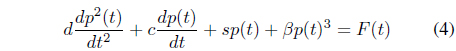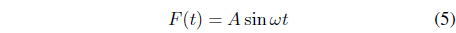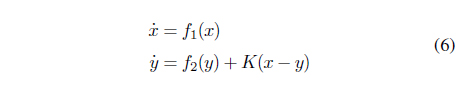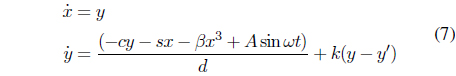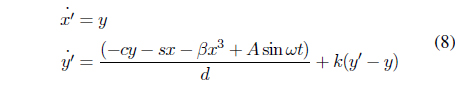In the last two decades, chaotic dynamics has been used widely in real-world applications, such as biological systems [1], brain modeling [2], weather modeling [3], vibration modeling [4], mechanical and electrical engineering [5, 6], control and synchronization [7-11], robotics [12, 13], and others [14-18]. Currently, it is also being studied by many researchers in biology, physics, sociology, psychology, physiology, and engineering. However, this research is not limited to the natural sciences, but is spreading to the social sciences, such as politics, economics, and the prediction of societal events such as happiness and addiction [14, 19].

Most people pursue happiness. However, happiness is not easy to define, because people differ in how they perceive it. Research in mathematical models of happiness has been conducted by many researchers including physicists, psychologists, engineers, physiologists, and mathematicians. Many mathematical models of happiness have been introduced [15-17]. Sprott [15] proposed dynamical models of happiness in 2004 and in 2005. He described a simple linear model, a lottery-winning model, a drug or other addiction model, and an anticipation model for arousing happiness. Sinha et al.[14] proposed a dynamics of love and happiness and discussed the stability of their proposed model.

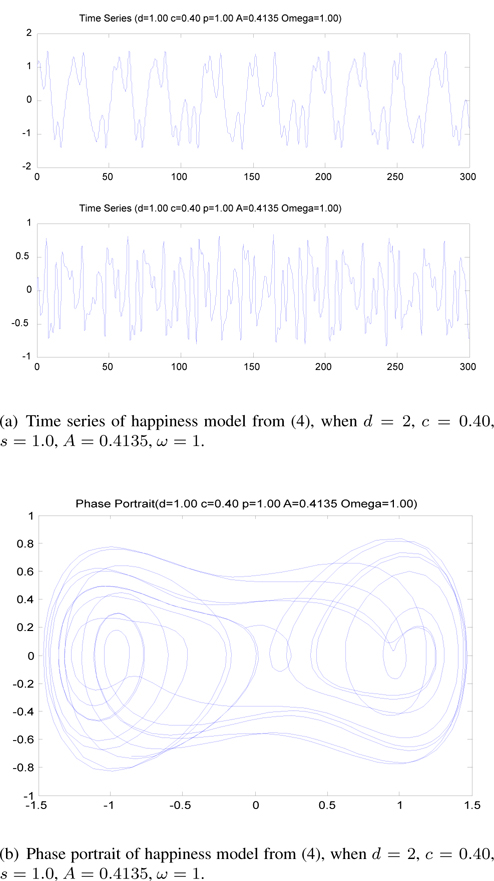
In this paper, we propose a chaotic synchronization method in a mathematical model of happiness organized by a secondorder ordinary differential equation with external force. This proposed mathematical happiness equation is similar to Duffing’s equation, as shown in Figure 1, because it is derived from that equation. We introduce our mathematical happiness model by using the derived Duffing equation, and then we demonstrate chaotic phenomena from the happiness model using a time series and phase portrait. We assume that the happiness model is divided into two parts, spiritual and physical.

To achieve chaotic synchronization between the human mind and body, we apply an idea of mind/body unity originating in Oriental philosophy. Of many chaotic synchronization methods [5-8], such as coupled, driven, coupled driven, phase, completed, and generalized synchronization, we use only coupled synchronization, because this method is closest to representing mind/body unity. Typically, coupled synchronization can be applied only to non-autonomous systems, such as a modified Duffing system. We represent the result of synchronization using a differential time series mind/body model.

The mathematical happiness models proposed by Sprott [15] in 2005 include simple linear, lottery-winning, drug and other addiction, real-life, nonlinear effect, and anticipation models. The formulation of happiness is given by Eq. (1).

where β is the damping (rate of decay), ω is the natural resonant frequency of oscillation in radians per unit time, and F(t) is an external power. Without loss of generality, we can assume ω = 1. Because ω = 2πf, we can measure time in units of .

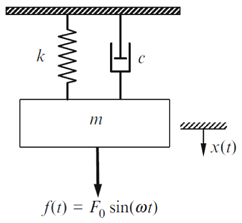
However, Eq. (1) does not provide an exact definition of a dynamical happiness model for each parameter. To describe exact variables in such a model, we must define the parameter that relates happiness and perception. This is similar to current in an electrical RLC series circuit and velocity in a mechanical spring-damper-mass system. Hence, we can apply those ideas in our dynamical happiness model to derive a new formula.

In this paper, we define happiness (H) as the amount of perception variation (dp) per amount of time variation (dt), as in Eq. (2).

where n is the amount of perception. Eq. (2) is equivalent to velocity in a spring-damper-mass model of a mechanical system. Perception in Eq. (2) includes human behavior, habituation, acclimation, and recognition adaption.

We define happiness (H) based on Eq. (2) to describe Eq. (3).

where c, d, and s represent control, desire and sense coefficients, respectively.

The control coefficient (c) represents the fact that when humans feel happy, the sense coefficient naturally reduces with passing time. If this value is zero, there is no other response, because the simple harmonic motion continues forever with the number of vibrations, . This situation is identical to the phenomenon of a frictionless mechanical system. Of course, if the value of the control coefficient is sufficiently large, there is no variation in feeling. If the control coefficient has a reasonable or small value, a human being can have feeling for a long time.

The desire coefficient represents a criterion of human desire. It is related to will and gratitude, which are person-dependent. If this value is sufficiently high, people tend to feel happy about minor things. As a result, their happiness will continue for a long time. The sense coefficients that represent the feeling of happiness differ greatly from person to person owing to differences in perceptivity.

In this paper, as vibrations result from the exchange of energy between the motion energy of a mass and the position energy of a spring in a spring-damper-mass system, we handle the occurrence of physical and mental fluctuation in terms of an exchange of energy or consciousness between the desire and sense coefficients in our dynamical happiness model.

With that theoretical background, we can finally derive a second-order equation for happiness with three independent parameters, the control, desire, and sense coefficients. This equation is given by (4).

where, F(t)is the power being applied externally. This external power is the cause of a happiness event. Examples may include periodic administration of medication or drugs, winning the lottery, or periodic gaming. In real life, it may be provided in the form of a sine or Gaussian wave. Periodic external power can be written as in Eq. (5).

From Eq. (4), we obtain a time series and phase portrait, as shown in Figures 2(a) and (b), respectively.

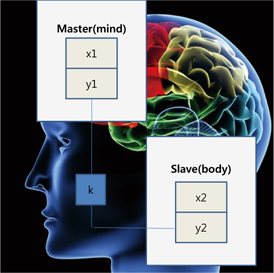
In this section, we establish a chaotic synchronization technique between mind and body in human beings using an Oriental philosophical idea of mind/body unity. To achieve mind/body synchronization, we assume that mind and body each has a chaotic model, such as a Duffing equation similar to Eq. (4). Figure 3 shows a human mind/body synchronization device.

From Figure 3, we can distinguish three synchronization methods, linearly coupled, driven, and coupled-driven. However, in this paper, because we consider only non-autonomous systems, the modified Duffing type, we need apply only linearly coupled synchronization. Because driven and coupled-driven synchronization can be used only with autonomous systems, we do not consider applying them to a modified Duffing type.

Linearly coupled synchronization in two identical systems has been studied in several papers [20, 21]. It can be described in general form by Eq. (6).

where , and K is a real nonnegative parameter.

The synchronization procedure is formulated to find K such that y(t) → x(t) for t → ∞. This means that the solution y(t) will be synchronized to the signal x(t).

To apply linear coupling to the human mind and body using the Duffing equation, we must define identical master and slave models as follows.

Master model

We assume that the master model is the mind model and that it can be expressed using the Duffing Eq. (7).

Slave model

We also assume that the slave model is the physical model and that it can be expressed using the Duffing Eq. (8).

From Eqs. (7) and (8), we must find a stable solution for k. To obtain a stable solution for k, we use the characteristic Eqs. (7) and (8) and find a stable area using the Routh-Hurwitz condition. We were able to get k > 0.10. In a human being, we can think of k as representing breathing or meditation.

Because we assume that the master is the mind and the slave is the body, the parts of this system can communicate with each other by recognizing a human being. Finally, the mind and the body can be synchronized through action recognition. For these situations, we will call these the oneness of mind and body.

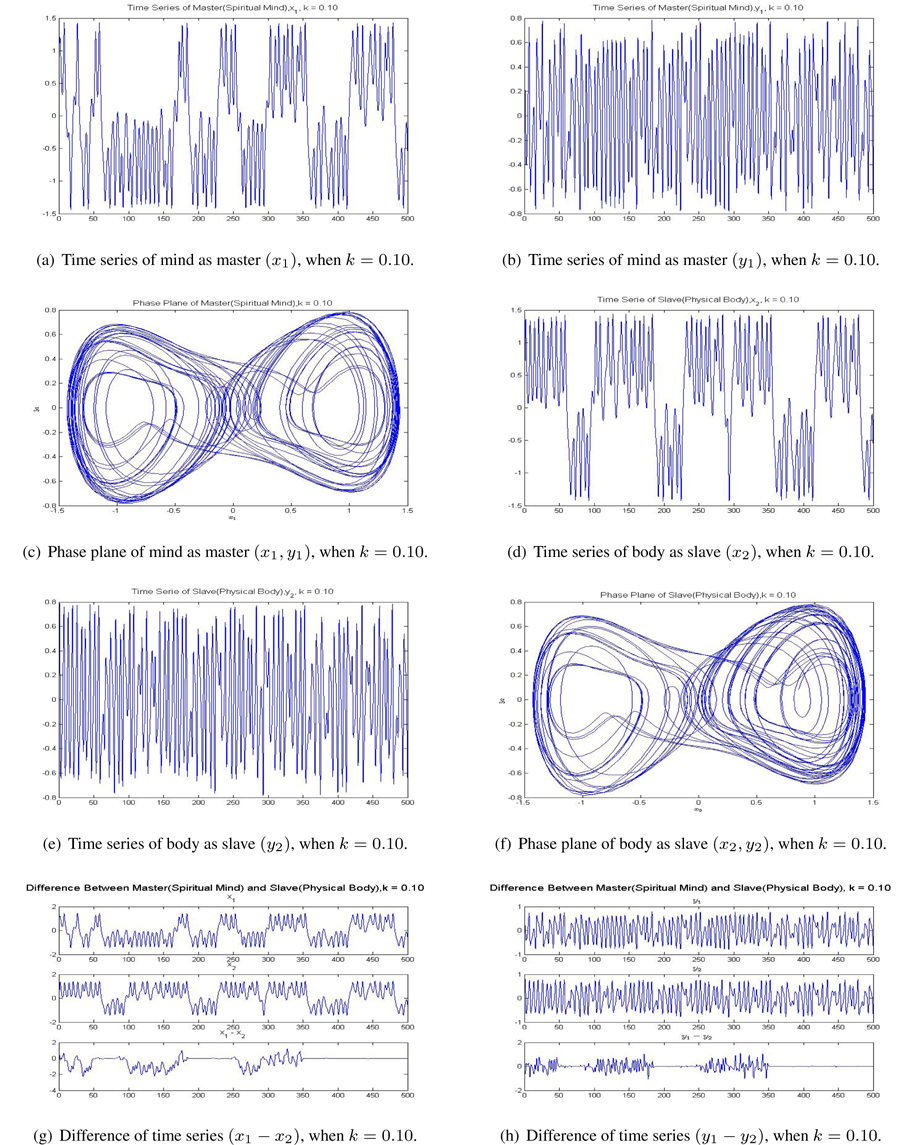
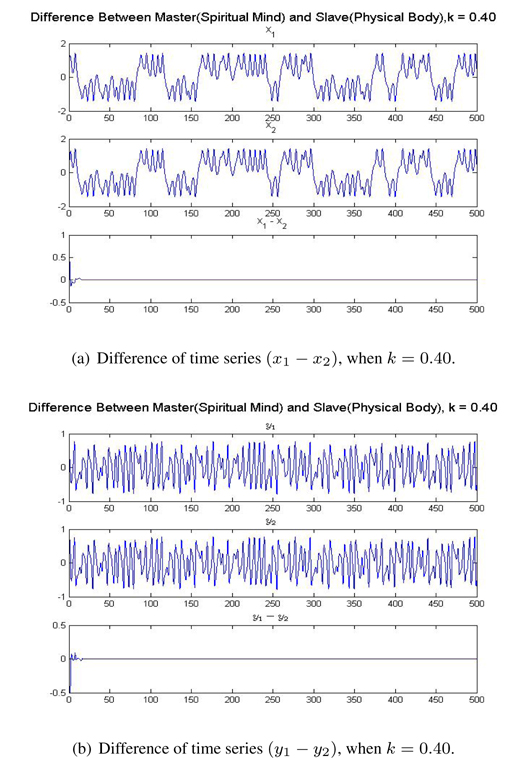
Figure 4 shows the results of mind/body synchronization, when k = 0.10. Figures 4(a) and (b) display (x₁, y₁) of a time series of the mind, respectively. Figure 4(c) represents (x₁, y₁) of the phase portrait of the mind. Figures 4(d) and (e) show x₂, y₂ of a time series of the body, respectively. Figure 4(e) represents (x₁, y₂) of the phase portrait of the body. Figures 4(f) and (g) show the results of synchronization as (x₁ − x₂) and (y₁ −y₂) of the differences of the time series, respectively.

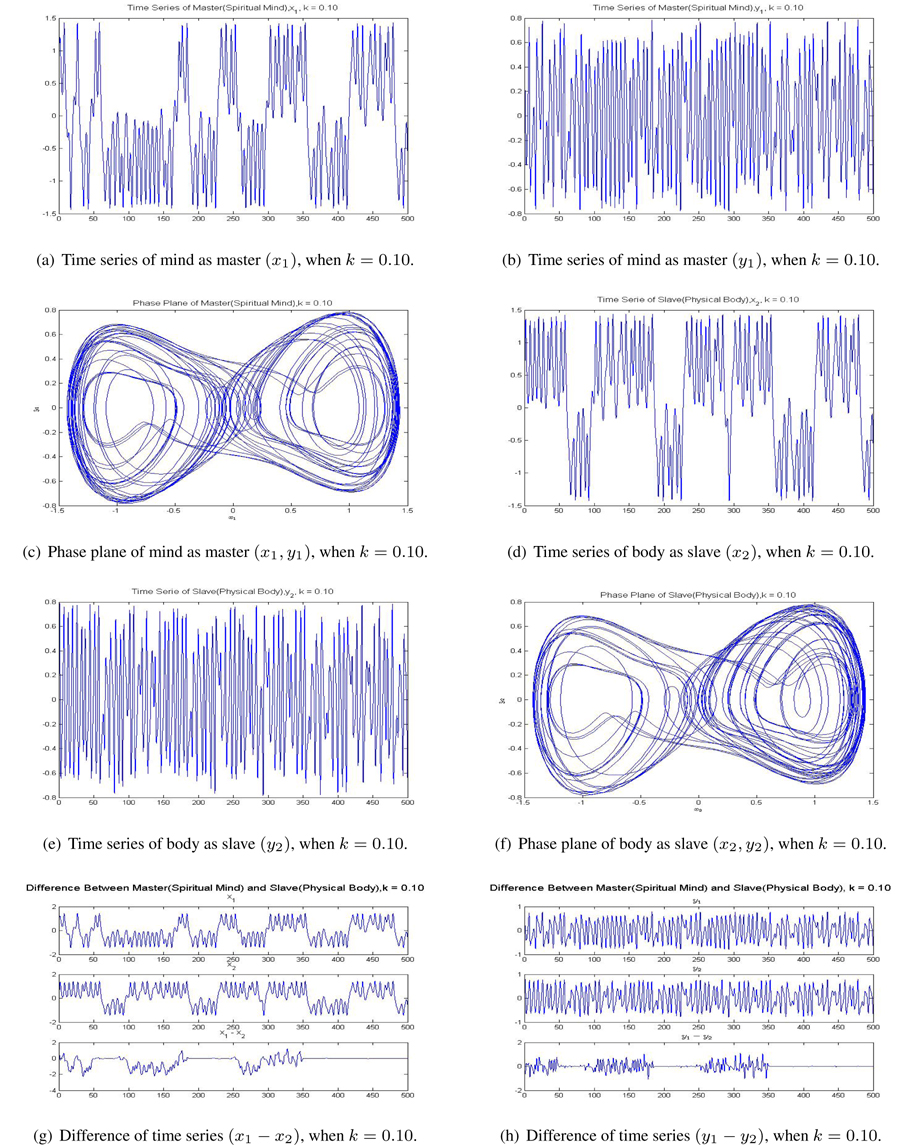
From Figure 4 we recognize that synchronization between mind and body is not achieved completely. This means that mind and body have not become one.

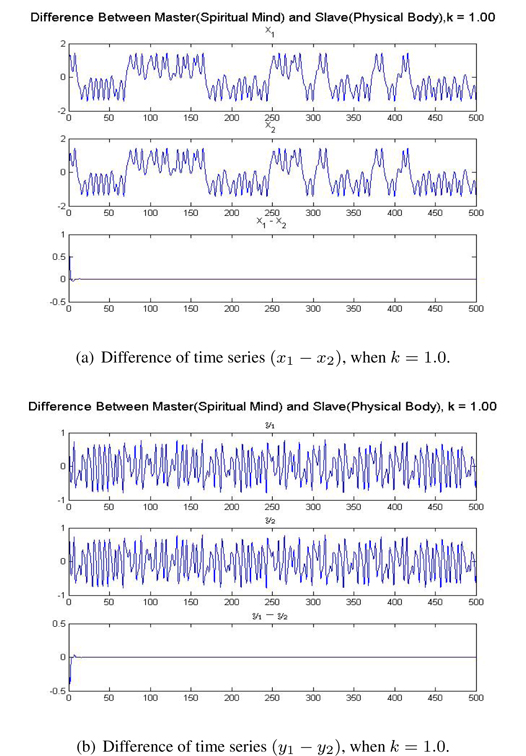
With the same condition, when we change to k = 0.40 and k = 1.0, we get the synchronization results shown in Figures 5 and 6, respectively.

From Figures 5 and 6, we see that synchronization between mind and body is achieved completely and is achieved more rapidly and fully, when the value of k is greater than 0.10. This means that mind and body have become one.

We proposed a chaotic synchronization method in a mathematical happiness model organized by a second-order ordinary differential equation with external force. This proposed mathematical happiness equation is similar to a modified Duffing’s equation and is derived directly from that equation. We applied linear coupling synchronization to the modified Duffing equation to demonstrate the result of synchronization by determining the feedback gain, k. Finally, we showed the result of synchronization through a time series and phase portrait of master and the slave models, as well as the difference of the two time series.