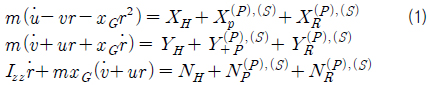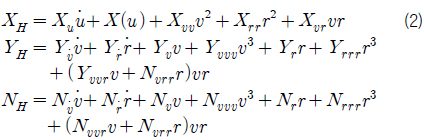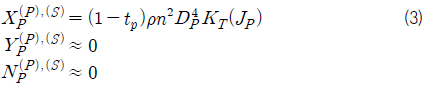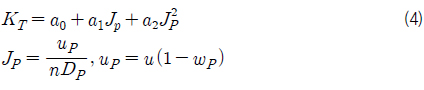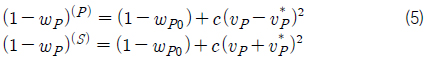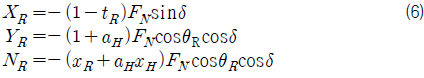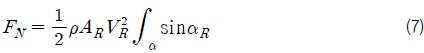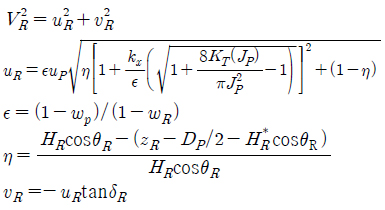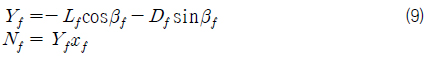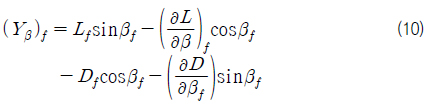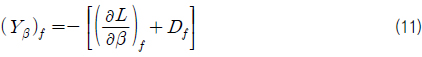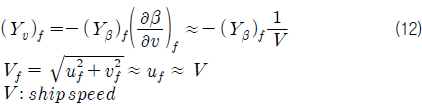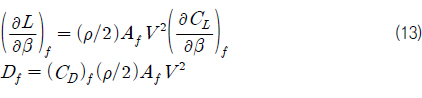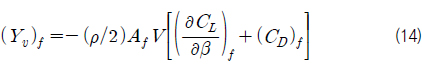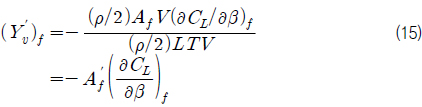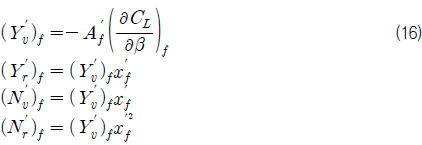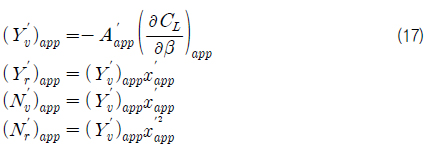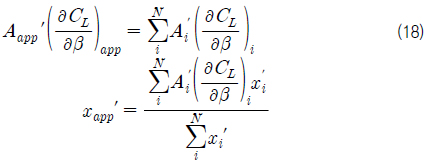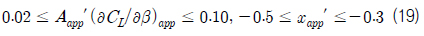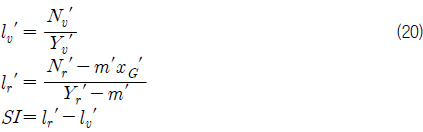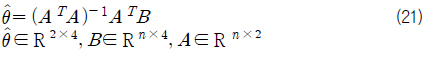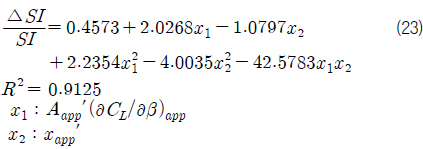Naval ships have hull appendages which are more exposed to the outside because of its small block coefficient compared with commercial ships. These exposed hull appendages like skeg, strut and shaft line affect the maneuverability of a ship. The effect of hull appendages has considered at initial design stage to estimate more accurate maneuverability. In this paper, sensitivity analysis is used to analyze the effect on maneuverability by hull appendages. 3 DOF maneuvering equations based on Mathematical Modelling Group (MMG) model are used and propeller & rudder model are modified to reflect the characteristics of twin propeller & twin rudder. Numerical maneuvering simulations (Turning test, Zig-zag test) for benchmark naval vessel, David Taylor Model Basin (DTMB) 5415 are performed. In every simulation, it is calculated that stability indices and maneuverability characteristics (Tactical Dia., Advance, 1st Overshoot, Time of complete cycle) with respect to the parameters (area times lift coefficient slope, attachment location) of hull appendages. As a result, two regression formulas are established. One is the relation of maneuverability characteristics and stability indices and the other is the relation of stability indices and hull appendages.
선박의 조종성능 추정은 설계 단계에서 수행되는 필수적인 부분이다. 특히나 함정은 상선에 비해 비교적 빠른 속도를 가지며, 실제 운용 중에 상선에서는 볼 수 없는 회피기동을 하기 때문에 더 좋은 조종성능이 요구되며, 그에 따라 초기 설계 단계에서 더 정확한 조종성능의 추정이 필요하다. 함정은 일반적으로 상선에 비해 더 많은 부가물들 (스케그, 스트럿, 샤프트 라인 등)이 부착되며, 작은 방형계수를 가진 탓에 넓은 면적이 바깥으로 노출되어 있다. 직진 안정성을 좋게 하기 위해 선미에 추가적으로 부착하는 스케그 외에 다른 부가물들도 역시 직진 안정성에 영향을 미친다. 그러므로 함정의 설계 단계에서 각 종 선체 부가물들이 조종성능에 미치는 영향을 반드시 고려해 주어야 한다.
함정은 일반적으로 2축2타 추진 시스템을 가지는데, 이 때문에 기존의 조종운동 수학모델은 다소 부정확한 부분들이 있다. 2축2타 상선의 조종성능 추정에 관한 선행 연구가 몇몇 있었다(Lee, et al., 1997; Sohn, et al., 2001; Lee, et al., 2003; Kim, et al., 2006). 실제 함정의 조종성능 추정 연구와 관련하여 대표적으로 사용되는 함정 공시선형 DTMB 5415 모델의 조종성능 추정에 관한 연구가 있었다 (Hess, et al., 2008; Miller, et al., 2008; Toxopeus, et al., 2008; Carrica, et al., 2013). 이에 비해 상대적으로 선체 부가물이 조종성능에 미치는 영향에 관련된 직접적 연구는 수행된 바가 많지 않다. Biandardi (1997) 는 선체 부가물에 의한 영향을 선체의 종방향 형상 변화로 고려하여 조종 성능 추정에 반영하였으며, Jacobs (1963) 와 Ankudinov (1993)는 선체 부가물이 조종성능에 미치는 영향을 선체와는 별개로 고려하여 조종성능 추정에 반영하였다. Lee, et al. (1998) 은 컨테이너선의 러더 및 부가물 그리고 선미형상을 변화시켜가며 구속모형시험을 수행하여, 부가물이 직진 안정성 향상에 미치는 영향을 실험적으로 입증하였다. 하지만 여기까지 연구된 내용에서 조종성능에 영향을 미치는 선체 부가물은 오직 스케그에 한정되어 있었으며, 스트럿이나 스테빌라이져 핀 등에 의한 영향은 고려되지 않아왔다. 이제까지의 조종성능 추정이 모두 상선에 그 초점이 맞추어져 있었는데, 스케그를 제외한 다른 부가물들의 면적이 상대적으로 작아서 조종성능에 미치는 영향이 작았기 때문이다. 다양한 부가물들에 대한 연구로써 Dubbioso, et al. (2013) 은 선미에 다양한 형상의 러더, 스케그 그리고 핀을 부착하여 모형 시험을 수행한 후, 이들이 조종성능에 미치는 영향에 대하여 고찰하였다. 민감도와 관련하여 잠수체의 조종성능에 적용한 연구 사례가 있다. Yeo, et al. (2005) 는 유체력 미계수와 상태변수와의 민감도 해석을 수행하였고 Yeo, et al. (2006) 는 형상 설계 인자들에 대한 안정성 지수의 민감도 해석을 수행하여 대표적인 조종성능 특성치들 (전술반경, 전진거리, 첫 번째 오버슈트, 두번의 오버슈트 이 후 선수각이 0으로 돌아오는데 걸리는 시간)에 실제로 어느 정도의 영향을 미치는지에 대해 알기가 어려웠다. 본 논문은 Jacob (1964) 의 연구에서 고정 핀이 유체력 미계수 변화에 미치는 영향을 참고하여, 선체 부가물이 상태변수가 아닌 조종성능 특성치들과의 민감도 해석을 수행한다. 선체 부가물의 변화에 따른 유체력 미계수 및 안정성 지수 (Stability index)의 변화를 살펴보고, 이를 이용하여 다시 안정성 지수와 조종성능 특성치와의 민감도 해석을 수행한다. 전역 민감도를 알아보기 위해해석적 방법이 아닌 수치적 방법에 의한 민감도 해석을 수행하고, 이를 위해 3 자유도 MMG 조종운동 수학모델을 사용한다. 최종적으로 선체 부가물 및 안정성 지수 그리고 조종성능 특성치들과의 수치적 관계를 정의한다.
본 논문의 구성은 다음과 같다. 2장에서는 2축2타 함정의 조종성능 추정을 위해 보정된 MMG 기반 조종운동 수학모델을 소개한다. 3장에서는 선체 부가물에 의한 유체력 미계수 변화에 대한 내용을 설명하고, 4장에서는 공시선형 DTMB 5415를 이용하여 조종운동 시뮬레이션 및 민감도 해석 결과를 분석한다. 얻어낸 수치 해석 결과를 회귀분석하여 조종성능 특성치와 안정성 지수 그리고 안정성 지수와 선체 부가물과의 관계식을 정의한다. 마지막으로 5장에서 결론으로 끝을 맺는다.
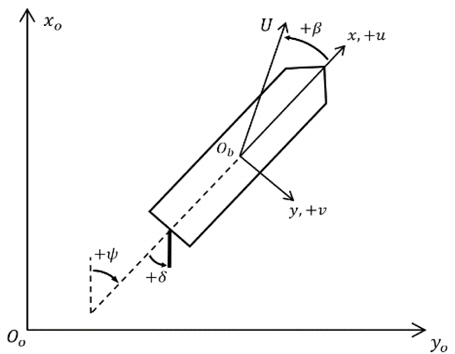
좌표계는 Fig. 1과 같이 지구고정좌표계
운동방정식 (1) 에서 아래 첨자 H, P, R 은 각각 선체, 프로펠러, 러더를 나타내고, G는 무게중심을 나타낸다. 위첨자 (P) 와 (S)는 각각 좌현 (Port) 과 우현 (Starboard) 을 나타낸다. 위첨자는 프로펠러 및 러더 모델에서 같은 의미로 사용한다.
프로펠러에 힘과 모멘트는 다음과 같다.
2축2타선에서는 좌우가 같은 프로펠러를 사용하므로 같은 추력계수
2축의 프로펠러가 중앙에서 벗어나 각각 좌와 우로 치우쳐져 있기 때문에 프로펠러 위치에서의 반류비가 좌우동요 속도에 대하여 좌우 대칭에서 비대칭이 된다. Lee et al. (2003) 을 참고하여 간단한 2차 다항식의 형태로 나타내었다.
러더에 의한 힘과 모멘트는 다음과 같다.
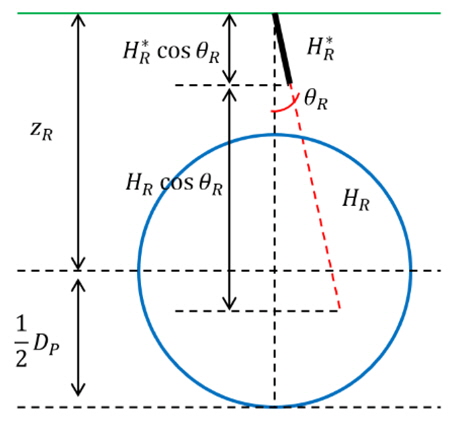
타직압력
여기서
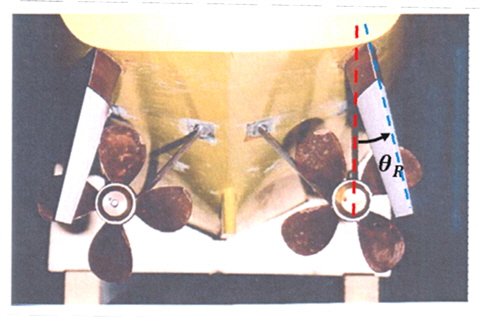
다양한 선체 부가물 중에서 조종성능에 영향을 미치는 선체 부가물들을 정의해야 한다. 선체 횡단면적에 비하여 무시할 수 없는 정도의 면적을 지닌 부가물들이 그 대상이 된다. Fig. 4 는 DTMB 5415 선미의 측면 사진인데, 조종성능에 영향을 미치는 부가물들을 표시하였다.
가장 왼쪽부터 스케그, 중간에 있는 것이 프로펠러를 지지하고 있는 스트럿, 그리고 러더스케그 부분이다. 이 외에도 선체 중앙 양 옆에 부착된 스태빌라이져 핀 역시 선체 부가물로써 고려된다.
선체 부가물들은 일종의 고정된 핀으로써, 일반적으로 선미 부근의 횡단면적을 커지는 역할을 한다. 이는 기존의 선체에 작용하던 유체의 압력중심을 더욱 후미로 옮겨가게 하여 직진 안정성을 증가시키는 효과를 가져온다. 이러한 고정된 핀에 의한 고려는 선체의 유체력 미계수에 반영될 수 있다. Jacobs (1964) 을 참고하여 고정된 핀에 의한 선형 유체력 미계수 유도과정을 살펴보도록 한다. 고정된 핀에 의해 발생하는 횡동요 힘
식 (9) 에서 횡동요 힘
(
이 때, (
식 (11) 에서 우변의 각 항들은 양력 계수 구배 (
식 (13) 를 식 (11) 에 대입하고, 식 (12) 을 이용하여 정리하면 다음과 같다.
미소한 유체 입사각에서 (
선체의 중심으로부터 고정된 핀이 부착된 위치 (고정된 핀의 압력중심 위치)를 사용하면 최종 무차원화된 고정 핀에 의한 4개의 선형 유체력 미계수 식을 얻을 수 있다.
식 (16) 를 통해 결국 고정된 핀, 즉 선체 부가물의 무차원화된 단면적과 양력계수구배와의 곱 그리고 선체의 중심으로부터 고정된 핀이 부착딘 위치 (고정된 핀의 압력중심 위치)에 의해 선체 부가물에 의한 선형 유체력 미계수가 표현된다.
민감도 해석이란 입력 변수의 변화에 대하여 출력 변수의 변화 정도에 대한 수치를 얻는 것을 일컫는다. 민감도 해석을 통해 입력 변수와 출력 변수와의 관계를 정의할 수 있으며, 이에 따라 얻고자 하는 출력변수의 값에 따른 입력변수의 변화를 예측할 수 있다. 민감도 해석 방법은 크게 수학모델을 변형시켜 얻은 민감도 미분방정식을 푸는 해석적 방법 (직접법)과 매개변수를 직접 변화시켜가며 수치모사를 수행하는 수치적 방법 (간접법)으로 나뉜다 (Saltelli, 2001). 해석적 방법은 수치적 방법에 비하여 정확하지만 국소 민감도를 얻는 데에만 적용할 수 있다. 본 연구에서의 입력 변수는 선체 부가물들의 면적 및 부착위치 등에 대한 정보인데, 이는 비교적 넓은 범위의 입력 변수 범위를 가지므로, 수치적 방법에 의한 민감도 해석을 수행하도록 한다
민감도 해석을 수행하기 앞서서 입력변수와 출력변수를 정의한다. 식 (16) 는 각각의 선체 부가물들을 고정된 핀으로 보고 나타낸 식이다. 실제 모든 선체 부가물들에 의한 영향을 하나의 부가물에 의한 영향으로 간주한다.
식 (17) 에서 각 파라미터들은 다음과 같이 정의한다.
입력변수는
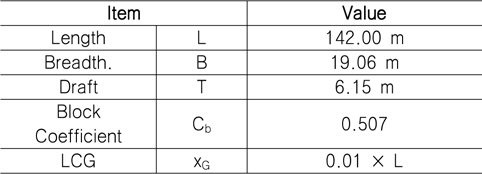
조종운동 시뮬레이션 수행을 위해 사용된 Hull 유체력 미계수는 구속모형시험을 통해 얻은 데이터를 이용하였다 (Benedetti, et al., 2006; Yoon, 2009). Table 1 은 DTMB 5415 모델의 실선 제원이다.
[Table 1] Principal dimensions of DTMB 5415
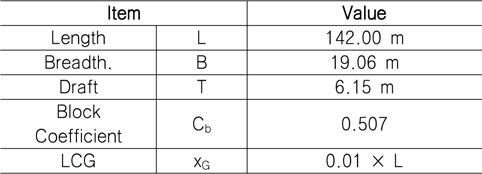
Principal dimensions of DTMB 5415
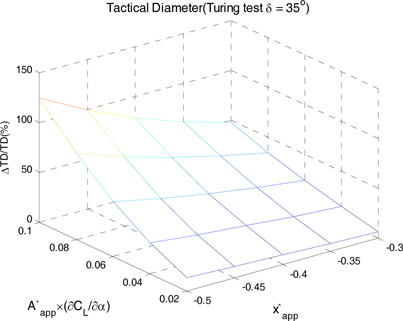
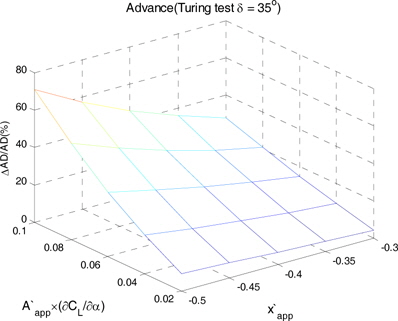
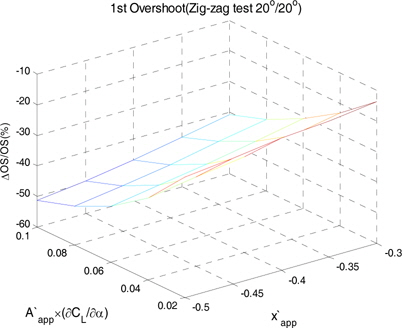
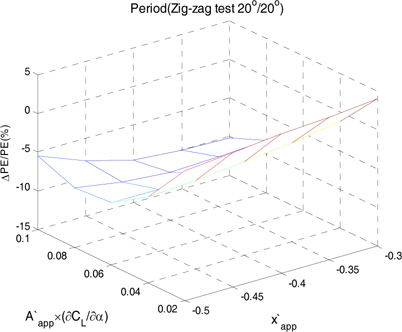
Fig. 5 ~ Fig. 8 은 앞 서 정의한 입력변수의 변화에 따른 조종성능 특성치들의 변화를 나타낸 것이다. 각각의 3차원 그래프에서 세로축이 0.0 값을 가리킬 때, 선체 부가물이 고려되지 않은 조종성능 특성치들이다. 전술반경이 최대 124%, 전진거리가 최대 71%, 첫 번째 오버슈트 각이 최대 51% 그리고 두 번의 오버슈트 이 후 선수각 0으로 돌아오는데 걸리는 시간이 10% 변화하였다. 이를 통해 선회 시험이 지그재그 시험에 비해 평균적으로 약 3배 이상 선체 부가물에 더 민감하게 변화함을 알 수 있다.
입력변수들의 절대값이 증가함에 따라 전술반경과 전진거리가 증가하고 첫 번째 오버슈트 각은 감소하였다. 하지만 두 번의 오버슈트 이 후 선수각이 0으로 돌아오는데 걸리는 시간은 안정성 지수가 음수인 구간에서는 감소하는 경향을 보였지만 양수인 구간에서는 뚜렷한 경향성을 보이지 않았다. 안정성 지수가 양수일 때에는 지그재그 시험 시 전진속도 감소량이 커서 오버슈트가 작더라도 시간은 크게 줄어들지 않는다고 볼 수 있다.
조종성능에서 직진 안정성을 판별하는 가장 대표적인 기준으로 선형 미계수들을 이용한 안정성 지수를 사용한다. 안정성 지수
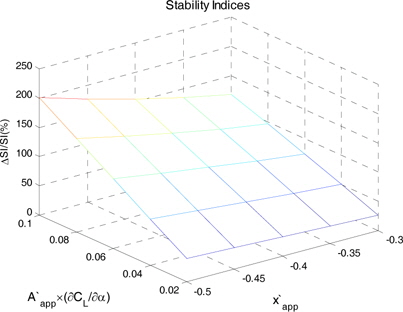
민감도 해석 입력변수의 변화에 따른 안정성 지수의 변화를 Fig. 9 에 나타내었다.
민감도 해석 입력변수의 절대값이 커질수록 안정성 지수 역시 그 값이 양의 방향으로 커졌으며, 최대 200%까지 변화하는 것을 볼 수 있다. 실제 선체만의 안정성 지수는 −0.2587 이며, 계산 결과 부가물에 의해 최소 −0.1902, 최대 0.2603 까지 증가하였다.
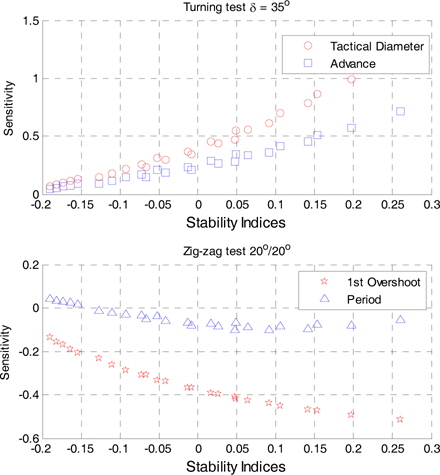
앞 서 구한 민감도 결과를 이용하여 조종성능 특성치와 안정성 지수와의 관계 그래프를 Fig. 10 에 나타내었다. 세로축의 민감도가 0.0 일 때가 선체 부가물의 영향이 고려되지 않은 값이다. 민감도가 아닌 실제 안정성 지수의 변화에 따른 민감도를 확인하기 위하여 실제 수치를 그대로 표기하였다.
안정성 지수와 조종성능 특성치들간의 관계를 수치적으로 정의하기 위해 선형 회귀분석을 수행하였다. 최소자승법을 사용하였으며, 다음과 같은 행렬의 형태로 계산하였다. 식 (21) 에서
식 (22) 에 결정계수
선형설계가 끝난 선박에 부가물들이 부착될 때, 스케그를 제외하고는 다른 부가물이 조종성능에 미치는 영향은 큰 고려대상이 아니다. 하지만 함정과 같이 큰 면적에 많은 수의 부가물이 부착되게 되면 조종성능에 많은 영향을 미치게 된다. 본 연구에서 민감도 해석을 통해 얻은 회귀식들은 부가물 설계 시 형상 및 부착 위치에 따른 선체 안정성 지수의 변화정도의 참고자료가 될 수 있다. 그리고 안정성 지수 변화에 따른 조종성능 특성치들의 변화를 직접적으로 추정하는데 역시 참고자료로 활용될 수 있다.
본 연구에서는 민감도 해석을 통하여 선체 부가물이 함정의 조종성능 특성치에 미치는 영향을 분석하였다. 조종운동 시뮬레이션을 위해 MMG 조종운동 수학모델을 사용하였으며, 2축2타 함정으로의 적용을 위해 몇몇 파라미터들을 추가하거나 보정하여 주었다. 수치적 방법을 통한 민감도 해석을 위해 입력변수들을 변화시켜가며 조종운동 시뮬레이션을 수행하고, 조종성능 특성치들의 변화양상을 비교하였다.
민감도 해석 수행 결과, 선회시험이 지그재그 시험에 비해서 선미 부가물의 변화에 더 민감함을 알 수 있었다. 선회시험 안에서는 전술반경이 직진거리보다 더 큰 영향을 받았으며, 지그재그시험 안에서는 첫 번째 오버슈트 각 만 영향을 받을 뿐, 두 번의 오버슈트 이 후 선수각이 0으로 돌아오는데 걸리는 시간은 뚜렷한 경향성을 보이지 않았다.
선체 부가물들의 변화에 따른 안정성 지수의 변화, 그리고 안정성 지수의 변화에 따른 조종성능 특성치 변화들의 수치적으로 관계를 정립하기 위해 회귀분석을 수행하였다. 이는 함정의 초기설계 단계에서 선체 부가물들이 조종성능에 미치는 영향을 추정할 때 유용하게 사용될 것으로 기대된다.
본 연구에서는 하나의 함정만을 이용해 수치적으로 부가물들이 조종성능에 미치는 영향을 분석하였다. 추가로 다른 함정들의 실험결과 및 부가물의 유무에 따른 실험결과들을 회귀분석에 추가한다면 더 신뢰성 있는 회귀분석을 얻을 수 있을 것이다.