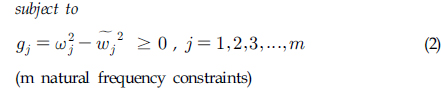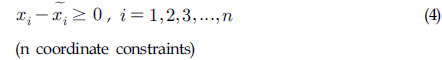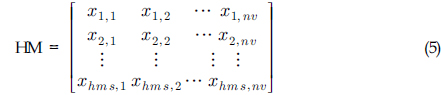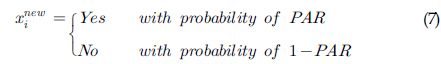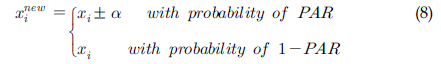하모니 서치 알고리즘과 고유진동수 제약조건에 의한 트러스의 단면과 형상 최적설계

doi:10.5574/KSOE.2013.27.5.036

OA학술지
Journal of Ocean Engineering and Technology

하모니 서치 알고리즘과 고유진동수 제약조건에 의한 트러스의 단면과 형상 최적설계 Optimum Design of Truss on Sizing and Shape with Natural Frequency Constraints and Harmony Search Algorithm

DOI : 10.5574/KSOE.2013.27.5.036
Publish: Journal of Ocean Engineering and Technology Volume 27, Issue5, p36~42, 31 Oct 2013

ABSTRACT

We present the optimum design for the cross-sectional(sizing) and shape optimization of truss structures with natural frequency constraints. The optimum design method used in this paper employs continuous design variables and the Harmony Search Algorithm(HSA). HSA is a meta-heuristic search method for global optimization problems. In this paper, HSA uses the method of random number selection in an update process, along with penalty parameters, to construct the initial harmony memory in order to improve the fitness in the initial and update processes. In examples, 10-bar and 72-bar trusses are optimized for sizing, and 37-bar bridge type truss and 52-bar(like dome) for sizing and shape. Four typical truss optimization examples are employed to demonstrate the availability of HSA for finding the minimum weight optimum truss with multiple natural frequency constraints.

KEYWORD

최적설계 , 고유진동수 , 하모니 서치 알고리즘

본문

Collapse all

1. 서 론

동적하중을 받고 있는 구조물은 비교적 낮은 진동수의 동적하중으로 인해 구조물에 심각한 손상을 준다. 특히 구조물의 고유진동수와 동적하중에 의한 진동수가 일치할 때 발생하는 공진으로 인해 구조물에 큰 피해를 발생 시킨다. 이처럼 구조물의 공진을 피하기 위해서는 우선 구조물의 고유진동수를 알아야 하며, 이를 바탕으로 구조물에서 동적하중에 의한 진동수와 구조물의 고유진동수가 일치하지 않도록 설계되어야 할 것이다. 그리고 진동수 제약을 사용하는 구조물 최적설계는 비선형문제가 되어 이를 해결하는 데는 많은 어려움이 따른다. 그런고로 수학적인 접근 방식보다는 확률론적인 알고리즘을 사용하는 것이 효율적이라 하겠다.

진동수 제약조건 및 형상 최적화에 의한 트러스의 최적설계는 Kaveh and Zolghadr(2012), Lingyun et al(2005), Gomes(2011), Wang et al.(2004), Sedaghati et al.(2002), Kim(2012), Park et al.(2005)등 많은 학자들에 의해 연구되었다. Kaveh and Zolghadr(2012)는 Charged system search - Big bang big crunch(CSSBBBC)방법을 사용하여 트러스의 단면 및 형상최적화를 연구하였다. Lingyun et al.(2005)은 동적제약조건을 고려한 트러스의 형상 및 단면의 최적설계에 Niche hybrid genetic algorithm(NHGA)을 사용하여 최적화 하였다. Gomes(2011)는 Partical swarm optimizer(PSO)방법을 사용하여 트러스의 단면 및 형상 최적화를 연구하였으며, Wang et al.(2004)은 Optimality criteria를 사용하여 트러스의 단면 및 형상을 최적설계 하였다. Sedaghati et al.(2002)는 진동수제약조건을 고려한 트러스와 프레임 구조물에 Finite element force method를 사용하여 수학적 알고리즘으로 최적설계 하였다. Kim(2012)은 고유진동수 제약과 유전자 알고리즘을 사용하여 트러스의 단면최적화를 연구하였다. Park et al.(2005)은 트러스의 단면과 형상에 대해 유전자 알고리즘을 사용하여 최적화 하였다.

본 연구에서는 고유진동수 제약조건을 적용한 트러스의 단면 및 형상 최적화를 연구하였다. 최적화 기법은 하모니 서치 알고리즘(Harmony search algorithm)을 사용 하였다. 하모니 서치 알고리즘은 확률론적 접근방식에 근거하여 주로 전공간 탐색에 매우 효과적으로 사용되는 검색방법이다. 이는 유전자 알고리즘은 이진수를 사용하지만 하모니 서치 알고리즘은 십진수를 사용한다는 점만 차이가 있을 뿐 최적화에서의 탐색 방법은 매우 유사하다. 특히, 하모니 서치 알고리즘은 일반적인 최적화기법과는 달리 최적화 과정에서 함수의 연속성 및 미분이 요구되지 않고 확 률적인 접근방법으로 비선형문제의 최적화문제에 아주 적합한 검색방법이라 하겠다. 최근에는 하모니 서치 알고리즘을 사용한 구조물의 최적화문제에 대한 연구도 많이 다루어지고 있다(Erdal et al., 2011; Saka, 2009; Lee and Geem, 2004).

본 연구에서 트러스 구조물의 설계예제에는 동적제약조건(고유진동수)과 최소단면 제약조건을 가지는 10-bar, 72-bar 트러스를 대상으로 하였으며, 37-bar 교량형 트러스와 Dome(52-bar)의 경우는 고유진동수 제약조건과 최소단면 및 형상 최적화를 위한 절점좌표의 제약조건이 적용되었다.

2. 구조물의 최적화 문제형성

구조물 최적화에는 다양한 설계조건들이 있으나 주로 비용이 최소가 되게 하든지 아니면 총무게가 최소가 되도록 설계하고 있다. 본 연구에서는 트러스의 총 무게가 최소가 되게 최적설계하였다. 최적설계에는 연속변수를 사용하여 단면 설계를 하였으며, 이 경우 목적함수(W)는 구조물의 총무게가 된다. 제약조건은 동적제약조건 즉 고유진동수와 단면 최소치수 및 절점좌표가 되며, 구조물의 최적설계에 대한 목적함수 W 및 제약조건식은 다음과 같다.

여기서,

ρi, Ai, Li ; i번째 부재에 대한 밀도, 단면적 및 길이 wj, ; j번째 고유진동수 및 주어진 특정고유진동수 Ai, ; i번째 부재의 단면적 및 최저 한계값 xi, ; i번째 절점좌표의 최저 한계값

10-bar 트러스에서는 3개의 고유진동수(w₁,w₂,w₃)와 최소단면 제약조건을 사용하여 무게가 최소가 되도록 최적설계 하였으며, 설계변수는 부재별 단면으로 모두 10개가 된다. 72-bar 트러스는 2개의 고유진동수(w₁, w₃)와 최소단면 제약조건을 사용하여 무게가 최소가 되도록 최적설계 하였다. 그리고 72개의 부재를 16의 그룹으로 분류해서 설계변수의 수를 16개로 하였다. 37-bar 트러스는 3개의 고유진동수 제약조건(w₁,w₂,w₃)과 14개의 단면변수 및 트러스의 상현재 절점의 y방향 5개의 좌표변수로 모두 19개의 설계변수를 사용하였다. 52-bar 트러스는 2개의 고유진동 수(w₁,w₂)와 최소단면 및 특정 절점에서의 이동거리 제한 제약조건을 사용하여 무게가 최소가 되도록 최적설계 하였다. 37-bar와 52-bar 트러스의 경우는 단면 및 형상 최적화로 설계하였다.

3. 하모니 서치 알고리즘

하모니 서치(Harmony search; HS) 알고리즘은 확률론적인 이론을 바탕으로 최적화문제를 해결하는 최적화기법이다. 하모니 알고리즘은 음악가가 보다 좋은 음악의 구성요소를 만들기 위한 과정을 수리 모델화시켜 문제를 해결하는 방법이다(Lee and Geem, 2004). HS알고리즘은 십진수를 사용하여 확률론적으로 해를 구하는 방법인데 이는 유전자 알고리즘에서 이진수를 사용하여 해를 구하는 방법과 매우 유사하다. 결국 HS알고리즘과 유전자 알고리즘은 Random process의 과정을 통해 확률론적으로 해에 접근하는 방법은 유사하나, 초기 설계집단을 구성하는 과정에 다 소 차이가 있다. HS알고리즘은 5단계의 과정으로 구성되며 아래와 같다.

Step 1. 초기값 설정

최적화문제의 해를 구하기 위한 초기값의 설정. 설계변수의 크기 및 변수의 최소값과 최대값의 설정, 하모니 메모리 크기(Harmony memory size, HMS)설정, 하모니 메모리 채택 비(Harmony memory considering ratio, HMCR)설정, 피치 조정비(Pitch adjusting ratio, PAR)설정, 전 과정의 반복횟수 설정. 그리고 일반적으로 비율 hmcr은 0.70-0.90의 사이 값을 사용하며, 비율 par은 0.2-0.5사이의 값 중에서 선택 할 수 있다. 이 비율은 문제의 성격에 따라 조정 할 수 있다.

Step 2. 하모니 메모리(Harmony memory, HM) 초기화

하모니 메모리의 초기화 단계. 초기값 설정단계에서 설계변수의 수와 HMS의 값에 의해 무작위 과정을 거쳐 HM을 초기화 시킨다(식 (5)). 이 초기화 과정에서 제약조건이 만족 되지 않은 값은 큰 페널티를 주어 HM에서 제외시킨다. 이 과정에서 설계 조건이 만족된 값들로 HM를 초기화 함으로서 보다 빠르게 해에 접근 할 수 있다. HMS는 유전자 알고리즘의 초기 설계집단의 구성과정과 매우 유사하다.

여기서 nv은 설계변수의 수이며, hms은 HM에서 설계집단의 크기이다.

Step 3. 새로운 하모니 메모리 구성

새로운 하모니 메모리의 구성단계. 새로운 HM은 확률 hmcr, par의 값에 따라 HM에서 설계들이 새로운 HM에 선택되는 기준의 판단 여부를 결정하는 과정이다. 확률 hmcr, par의 값은 0과 1사이의 Random수이다. 새로운 HM을 구성하기위한 설계는 아래 식의 조건으로 만들어진다.

이 과정은 확률 hmcr과 par에 따라 이전 단계의 하모리 메모리에서 새로운 HM을 구성하는 과정이며, 우선 Random수와 hmcr을 비교하여 Random수가 hmcr보다 적을 경우 HM의 설계가 새로운 HM의 설계로 선택 되고, 그렇지 않으면 Random과정을 거쳐 새로운 HM을 구성한다(식 (6)). 그리고 위의 과정에서 선택된 설계중 다시 Random수와 확률par를 비교하여 Random수가 par보다 적을 경우 설계를 다시 수정하여 새로운 HM을 구성한다(식 (7)). 이 과정에서 HS는 확률 hmcr, par를 사용하여 전공간 설계 또는 보다 개선된 국지설계를 찾을 수 있다. 그리 고 이 단계는 유전자 알고리즘에서 번식, 교차, 돌연변이를 사용하는 과정과 유사하다.

Step 4. 하모니 메모리 업데이트

새로운 HM이 구성된 후 각각의 설계변수에 해당되는 설계값을 구하여 HM을 업데이트 하는 과정이다. 이 과정에서 설계값을 서로 비교하여 가장 나쁜 값은 HM에서 제외하고 새로운 설계로 업데이트되는 과정이다. 그리고 HM에 가장 우수한 값부터 차례로 설계값을 나열한다.

Step 5. Step 3과 Step 4의 반복과정

Step 3과 Step 4가 주어진 반복수만큼 반복 작업을 통해 해를 구하는 단계이다.

4. 구조물의 최적화 과정

고유진동수 제약조건을 사용한 트러스의 단면 및 형상최적화에 HS알고리즘을 사용하였다. 본 연구에서 최적화 과정에 사용된 계수들과 HS의 과정을 구성단계별로 알아본다.

Step 1. HS알고리즘에 사용 된 초기값 설정. 설계 변수의 수 설정으로 10-bar 트러스는 10개의 설계변수이며, 72-bar 트러스는 16개의 설계변수로 하였다. 37-bar 트러스는 14개의 단면변수와 5개의 좌표변수를 사용하였고, 52-bar 트러스는 8개의 단면 설계변수와 5개의 절점 좌표로 설계변수를 13개로 하였다. 그리고 모든 예제에서 사용된 HMS의 크기는 30이며, 확률 hmcr과 par은 0.9와 0.3로 하였다.

Step 2. 새로운 HM을 구성하는 과정. 이 과정에서 확률 hmcr에 의해 선택된 설계들 중에서 다시 확률par에 해당되는 설계를 선택한 후 선택된 이 설계들의 십진수를 업데이트 한다(식 (8)).

여기서, α는 x_i의 증분 값이며, 주로 1을 사용한다. 본 연구에서는 증분 α에 1보다 적은 Random수를 사용하였다. 식 (8)은 설계 x_i에 이웃하는 또 다른 설계를 증분값 α로 셈플링하여 보다 개선된 해를 구하는 과정이다. 이 과정을 통해 또 다른 국지해를 구할 기회가 주어된다.

3. 본 연구에서는 α에 Random수를 사용하며, 초기 HM구성과정에서 제약조건을 모두 만족하는 설계들로만 HM이 구성 되도록 하여 해의 수렴상태를 증가 시키는 방법을 제시하였다.

구조물의 최적화 과정에는 Linux o/s 인 Fedora ver. 17을 기반으로 Fortran프로그램을 사용하였다.

5. 설계예제

   5.1 10-bar 트러스

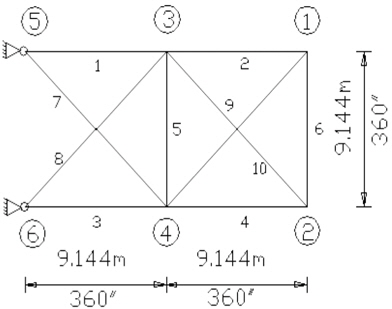
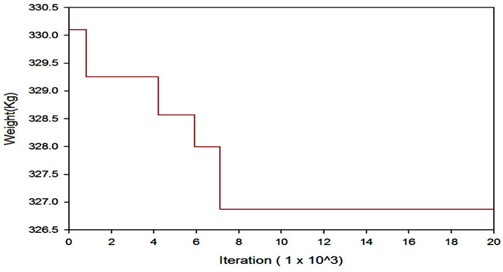
10-bar 트러스의 제원은 아래 Fig. 1과 같으며, 재료의 탄성계수E=7.03x10⁵Kg/cm², 부재의 밀도 ρ=2770k/m³등의 값을 사용하였으며, 10개의 연속변수를 사용하여 최적설계 하였다. 모든 부재에서 단면의 최소값은 0.645 cm²로 하였으며, 4개의 절점(Node 1, 2, 3, 4)에 454kg의 질량을 첨가 하였다. 동적제약조건인 고유진동수 w₁≥7.0Hz, w₂≥15.0Hz, w₃≥20.0Hz가 적용되었으며, 총무게가 최소가 되게 최적 설계하였다. Table 1은 본 연구에서 제시된 HS알고리즘에 의한 최적 설계결과이다. Table 2는 고유진동수에 대한 최적 설계결과이며, 제약조건(w₁,w₂,w₃)을 모두 만족하였고, 초기 8개의 고유진동수도 비교적 만족한 결과를 얻었다. Table 1의 결과로부터 여러 연구결과를 비교하여 본 연구에서 제시된 HS알고리즘을 사용한 경우가 개선된 설계결과를 얻을 수 있었으며, Kaveh and Zolghadr보다 8.107%의 개선된 결과를 얻었다. HS알고리즘에서 반복 횟수는 50000이며, Fig.2는 해의 수렴 상태이다. Fig. 2는 3가지의 조건을 달리한 해의 수렴 상태로 본 연구에서 제시한 방법이 비교적 안정적으로 해에 수렴함을 볼 수 있다.

[Fig. 1] Configuration of 10-bar truss

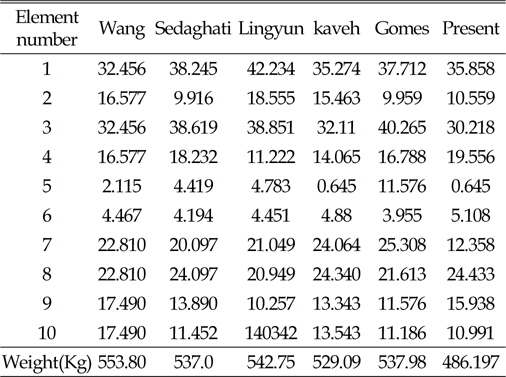
[Table 1] Optimum design of cross-sectional(cm2) of 10-bar truss

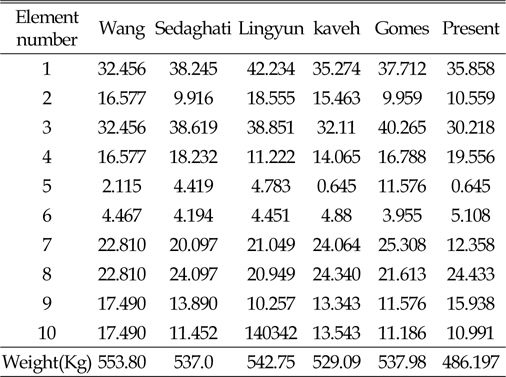
Optimum design of cross-sectional(cm2) of 10-bar truss

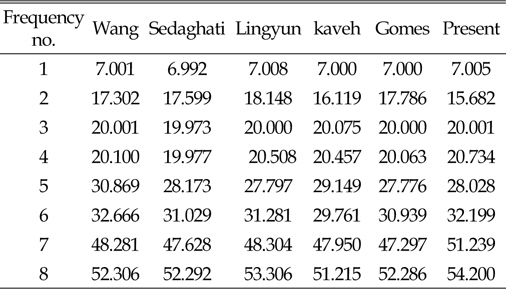
[Table 2] Natural frequency(Hz) of 10-bar truss

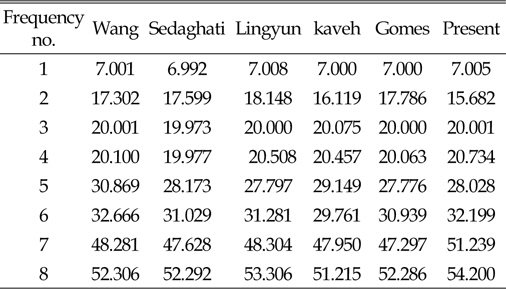
Natural frequency(Hz) of 10-bar truss

[Fig. 2] Iteration of 10-bar truss

   5.2 72-bar 트러스

72-bar 트러스의 제원은 아래 Fig. 3과 같으며, 재료의 탄성계수E=7.03x10⁵Kg/cm², 부재의 밀도 ρ=2770kg/m³의 값을 사용하였으며, 72개의 부재를 그룹별로 16개의연속변수를 사용하여 최적설계 하였다. 모든 부재에서 단면의 최소값은 0.645cm²로 하였으며, 4개의 절점(Node 1, 2, 3, 4)에 2270kg의 질량을 첨가하였다. 동적제약조건인 고유진동수 w₁=4.0Hz, w₃≥6.0Hz가 적용되었다. Table 3은 HS알고리즘에 의한 최적 설계결과이며, Gomes보다는 0.43% 개선된 설계결과를 얻었다. Table 4는 고유진동수에 대한 설계결과이며, 동적제약조건을 모두 만족하였다. Fig. 4는 해의 수렴 상태이다.

[Fig. 3] Configuration of 72-bar truss

[Table 3] Optimal design of 72-bar truss(cm2).

Optimal design of 72-bar truss(cm2).

[Table 4] Natural frequency(Hz) of 72-bar truss

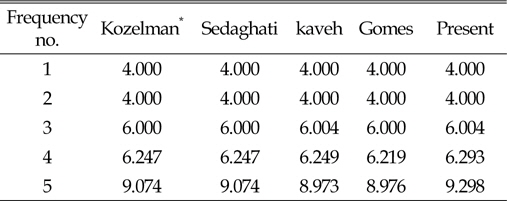
Natural frequency(Hz) of 72-bar truss

[Fig. 4] Iteration of 72-bar truss

   5.3 37-bar 트러스

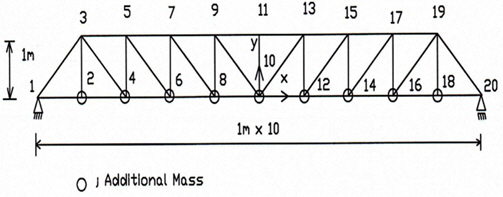
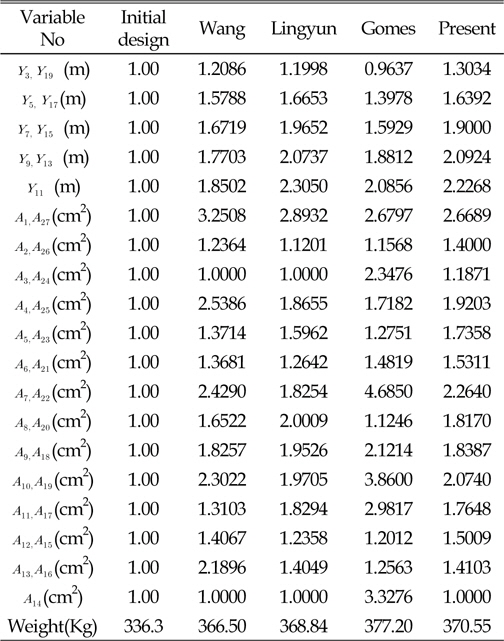
37-bar 트러스의 제원은 아래 Fig. 5와 같으며, 재료의 탄성계수E=2.1×10¹⁰N/m², 부재의 밀도 ρ=7800kg/m³의 값을 사용하였으며, 37개의 부재중 트러스의 하현재는 단면적(50cm×80cm)을 일정하게 하였다. 하현재를 제외한 부재는 구조물의 대칭성을 하현재의 절점에는 10kg의 질량을 첨가 하였다. 제약조건인 고유진동수는 w₁≥20.0Hz, w₂≥40.0Hz, w₃≥60.0Hz가 적용되었다. Table 5는 HS알고리즘의 최적 설계결과이며, Wang, Lingyun의 결과 보다는 높게 나왔으나 Gomes보다는 1.8% 개선된 결과를 얻었다. Table 6은 고유진동수에 대한 설계결과이며, 동적제약조건을 모두 만족하였다. Fig. 5는 초기값에 의한 형상이며, Fig. 6은 Wang에 의한 결과이다. Fig. 7은 HS알고리즘을 사용하여 최적화된 결과의 형상이며, Fig. 8은 해의 수렴 상태이다.

[Fig. 5] Initial Configuration of 37-bar truss

[Fig. 6] Optimized shape in Wang

[Fig. 7] Optimized shape by HA algorithm

[Table 5] Optimum design of cross-sectional(cm2) and y-coordinates (m) of 37-bar truss

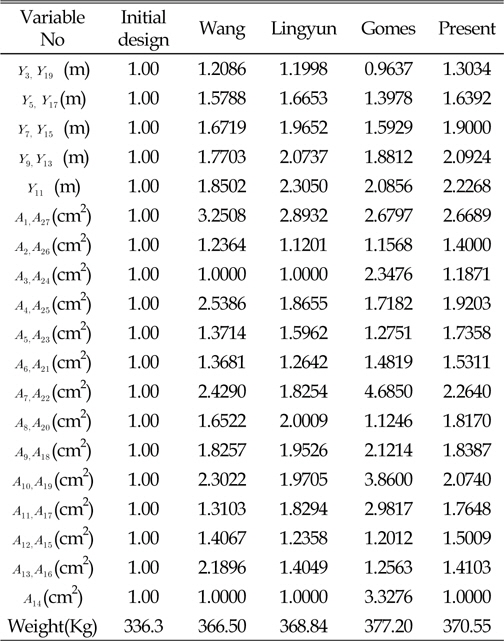
Optimum design of cross-sectional(cm2) and y-coordinates (m) of 37-bar truss

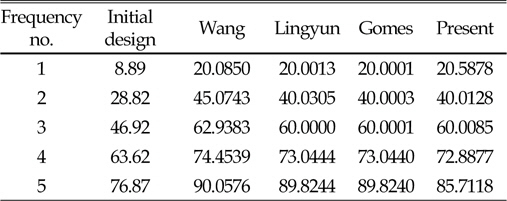
[Table 6] Natural frequency(Hz) of 37-bar truss

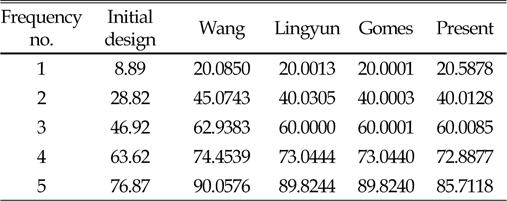
Natural frequency(Hz) of 37-bar truss

[Fig. 8] Iteration of 37-bar truss

   5.4 52-bar 트러스(Dome형)

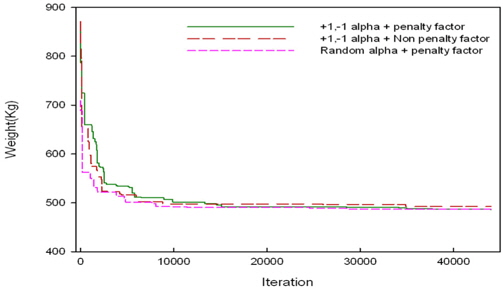
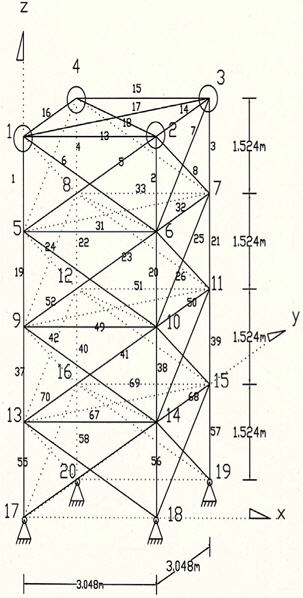
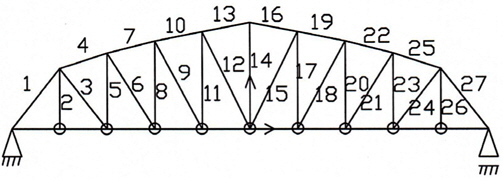
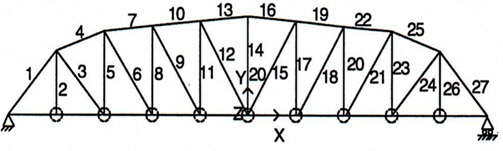
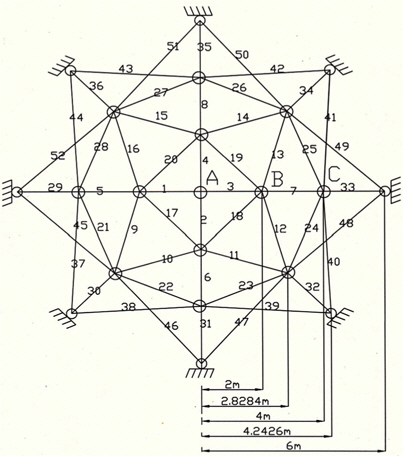
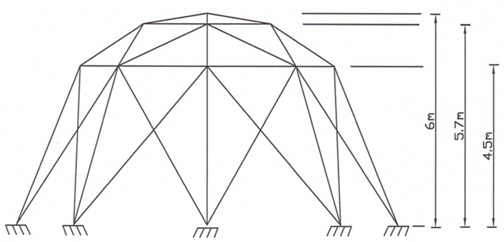
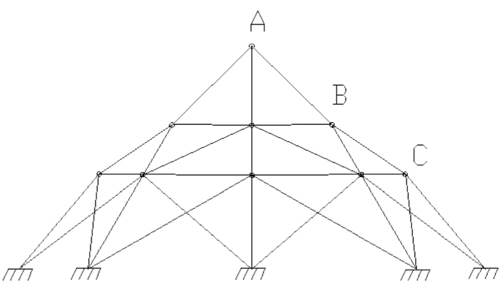
52-bar 트러스의 제원은 아래 Fig. 9와 같으며, 재료의 탄성계 수E=2.1×10¹⁰N/m², 부재의 밀도 ρ=2770kg/m³의 값을 사용하였으며, 52개의 부재를 그룹별로 8개변수와 절점(A,B,C)에서의 x,y,z좌표변수 5개로 하여 총설계변수를 13개로 하여 최적설계하였다. 그리고 절점변수는 상,하 그리고 좌,우 모두가 대칭되는 절점은 같은 좌표를 사용한다. 모든 부재에서 단면의 최소, 최대값은 1.0cm²에서 10.0cm²로 하였으며, 구속되지 않는 절점 모두에 50kg의 질량을 첨가 하였다. 동적제약조건인 고유진동수 w₁≤15.916Hz, w₃≥28.648가 적용되었다. Table 7은 HS알고리즘에 의한 최적설계결과이며, Gomes의 결과 보다는 16.2% 개선된 결과를 얻었다. Table 8은 고유진동수에 대한 설계결과이며, 동적제약조건을 모두 만족하였다. Fig. 10은 초기상태의 형상이며, Fig. 11은 HS알고리즘을 사용하여 최적화된 결과의 형상이다. Fig. 12는 해의 수렴상태이다.

[Fig. 9] Configuration of 52-bar truss structure

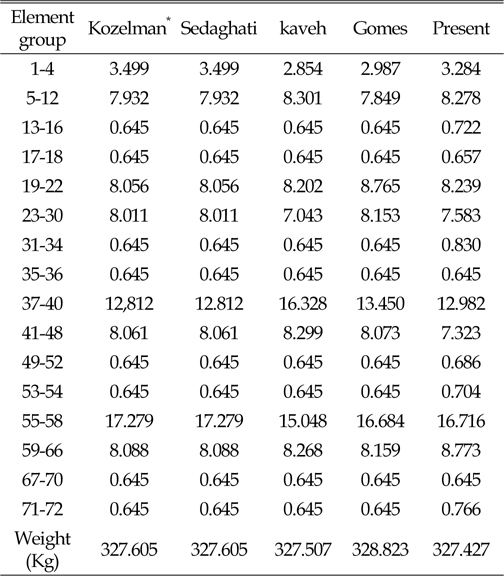
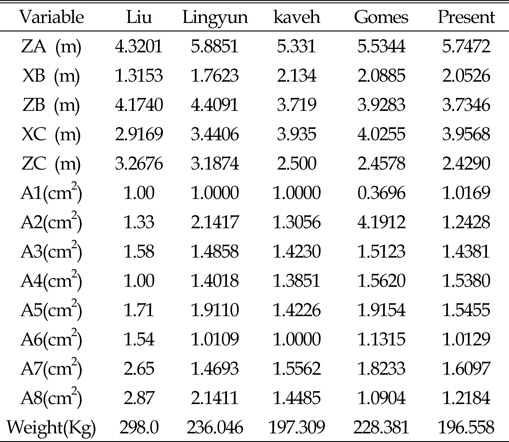
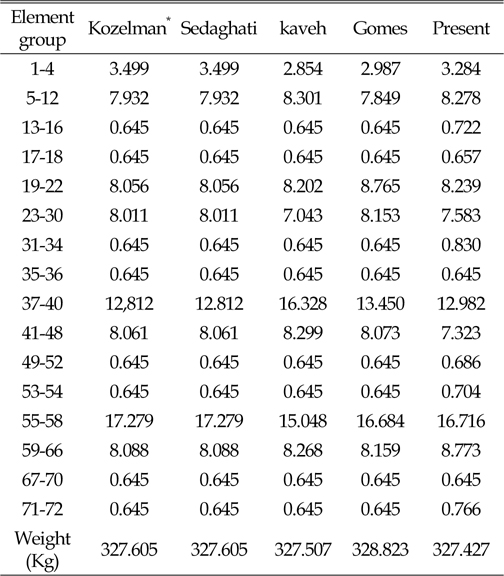
[Table 7] Optimum design of 52-bar truss

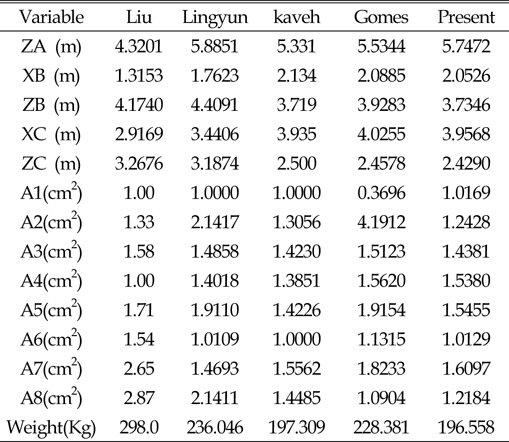
Optimum design of 52-bar truss

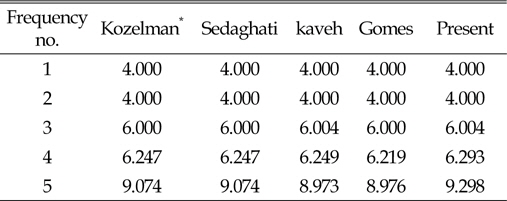
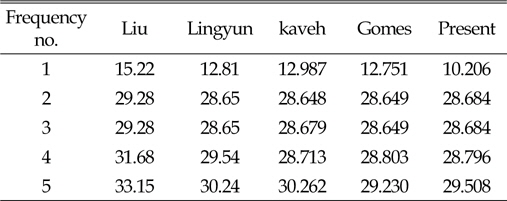
[Table 8] Natural frequency(Hz) of 52-bar truss

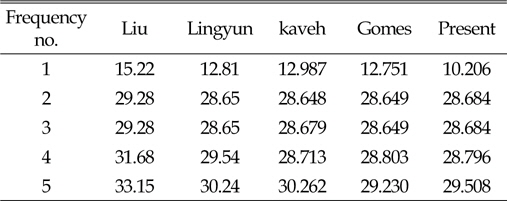
Natural frequency(Hz) of 52-bar truss

[Fig. 10] Initial configuration of 52-bar truss(side view)

[Fig. 11] Optimized shape of 52-bar truss

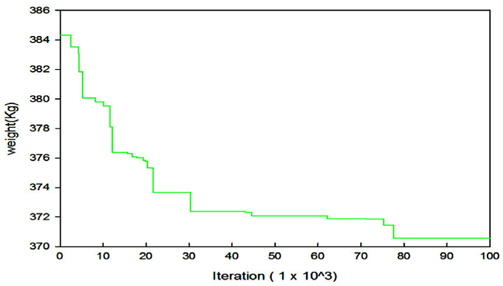
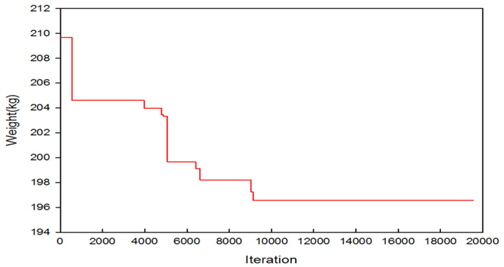
[Fig. 12] Iteration of 52-bar truss

6. 결 론

동적하중을 받는 구조물은 낮은 진동수의 동적하중으로 인해 구조물에 심각한 손상을 준다. 이 경우 구조물의 고유진동수와 동적하중에 의한 진동수가 일치할 때 발생하는 공진현상으로 인해 구조물에 큰 피해를 발생 시킨다. 구조물의 공진현상을 피하기 위해서는 우선 구조물의 고유진동수를 알아야 하며, 이를 바탕으로 구조물에서 동적하중에 의한 진동수와 구조물의 고유진동수가 일치하지 않도록 설계되어야 할 것이다. 본 연구에서는 고유진동수 제약에 의한 트러스구조물의 단면과 형상최적설계를 연구하였다. 트러스의 최적설계에는 연속변수를 사용하였으며, 최적화 기법으로는 업데이트과정중 Random수를 사용한 HS알고리즘을 사용하였다. 트러스의 단면 최적설계에는 10-bar, 72-bar를 사용 하였으며, 단면 및 형상 최적설계에는 37-bar, 52-bar로 네 경우를 사용하였다. 10-bar 트러스의 경우 CSS-BBBC방법을 사용한 Kaveh and Zolghadr의 결과보다는 8.1%, 72-bar의 경우는 Gomes의 결과 보다는 0.43% 개선된 설계값을 구하였다. 37-bar 트러스의 경우 Wang, Lingyun의 결과와 유사하나 Gomes의 결과 보다는 1.8%의 개선된 값을 얻었다. 52-bar 트러스의 경우는 Gomes의 결과 보다는 16.2% 개선된 결과를 얻을 수 있었다. 지금까지의 예로 사용한 결과와 여러 연구결과를 비교하여 본 연구에서는 HS알고리즘의 초기 메모리 구성과정에 제약조건이 만족되는 설계만을 사용하고, 업데이트과정중 Random수를 증분값(α)으로 사용하는 최적화방법을 제시하였으며, 이 방법의 실용성과 적용성을 보였다. 결론적으로 HS알고리즘은 확률론적 방법으로 전공간 최적화의 해를 구하는 방법으로 함수의 미분값이 요구되지 않으며, 설계변수의 수 및 여러 제약조건 등에 많은 제약을 받지 않는 단순 수리 과정임을 고려하면 현실적인 트러스 구조물의 최적화문제에 매우 적합한 방법이라 하겠다.

참고문헌

1. Erdal F., Dogan E., Saka M.P. 2011 Optimum Design of Cellular Beams using harmony Search and Partical Warm Optimizer [Journal of Constructional Steel Research] Vol.67 P.237-247
2. Gomes H.M. 2011 Truss Optimization with Dynamic Constraints using Partical Swarm Algorithm [Expert System with Application] Vol.38 P.957-968
3. Kaveh A., Zolghadr A. 2012 Truss Optimization with Natural Frequency Constraints using Hybridized CSS-BBBC Algorithm with Trap Recognition Capability [Computer & Structures] Vol.102-103 P.14-27
4. Kim B.I. 2012 Optimum Design of Steel Structures Using Genetic Algorithms [Journal of Korean Society of Steel Construction, KSSC] Vol.24 P.701-710
5. Lee K.S., Geem Z.W. 2004 A New Structural Optimization Method Based on the Harmony Search Algorithm [Computer & Structures] Vol.82 P.781-798
6. Lingyun W., Mei Z., Guangming W., Guang M. 2005 Truss Optimization on Shape and Sizing with Frequency Constraints Based on Genetic Algorithm [Computer Mechanics] Vol.35 P.361-368
7. Park C.W., Kang M.M., Yun Y.M. 2005 Unified Section and Shape Discrete Optimum Design of Planar Improved Fuzzy Genetic Algorithms [Journal of Korean Society of Steel Construction, KSSC] Vol.1794 P.385-394
8. Saka M.P. 2009 Optimum Design of Steel Sway Frames to BS5950 using Harmony Search Algorithm [Journal of Constructional Steel Research] Vol.65 P.36-43
9. Sedaghati R., Suleman A., Tabarrok B. 2002 Structural Optimization with Frequency Constraints Using the Finite Element Force Method [AIAA] Vol.40 P.382-388
10. Wang D., Zhang W.H., Jiang J.S. 2004 Truss Optimization on Shape and Sizing with Frequency Constraints [AIAA Journal] Vol.42 P.622-630

이미지 / 테이블

[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 1 ] Configuration of 10-bar truss
[ Table 1 ] Optimum design of cross-sectional(cm2) of 10-bar truss
[ Table 2 ] Natural frequency(Hz) of 10-bar truss
[ Fig. 2 ] Iteration of 10-bar truss
[ Fig. 3 ] Configuration of 72-bar truss
[ Table 3 ] Optimal design of 72-bar truss(cm2).
[ Table 4 ] Natural frequency(Hz) of 72-bar truss
[ Fig. 4 ] Iteration of 72-bar truss
[ Fig. 5 ] Initial Configuration of 37-bar truss
[ Fig. 6 ] Optimized shape in Wang
[ Fig. 7 ] Optimized shape by HA algorithm
[ Table 5 ] Optimum design of cross-sectional(cm2) and y-coordinates (m) of 37-bar truss
[ Table 6 ] Natural frequency(Hz) of 37-bar truss
[ Fig. 8 ] Iteration of 37-bar truss
[ Fig. 9 ] Configuration of 52-bar truss structure
[ Table 7 ] Optimum design of 52-bar truss
[ Table 8 ] Natural frequency(Hz) of 52-bar truss
[ Fig. 10 ] Initial configuration of 52-bar truss(side view)
[ Fig. 11 ] Optimized shape of 52-bar truss
[ Fig. 12 ] Iteration of 52-bar truss