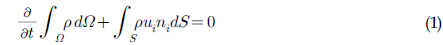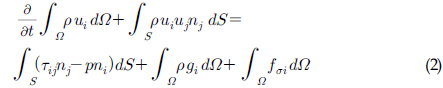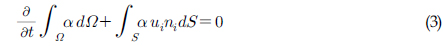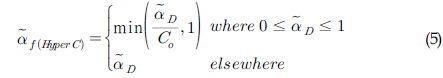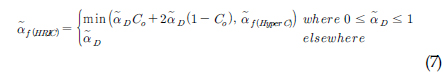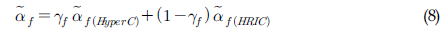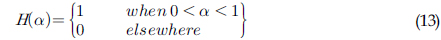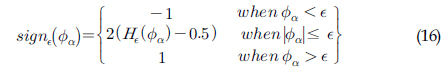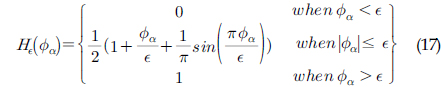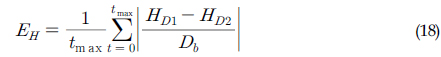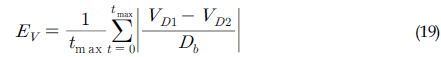The present paper proposes a coupled volume‐of‐fluid (VOF) and level‐set (LS) method for simulating incompressible two‐phase flows that include surface tension effects. The interface of two fluids and its motion are represented by a VOF method designed using high‐resolution differencing schemes. This hybrid method couples the VOF method with an LS distancing algorithm in an explicit way to improve the calculation of the normal and curvature of the interface. It is developed based on a rather simple algorithm to be efficient for various practical applications. The accuracy and convergence properties of the method are verified in a simulation of a single gas bubble rising in a three‐dimensional flow with a large density ratio.
이상유동(Two-phase flow) 해석법으로서 VOF(Volume of fluid)법은 선박과 해양공학 분야의 관심 유동 현상인 조파(Wave making) 문제 해석은 물론, 그린워터(Green water), 슬로싱(Sloshing), 슬래밍(Slamming) 등의 복잡한 비선형 자유수면 유동 해석에 있어 유용하고 신뢰할 만한 결과를 제공하는 수치기법들 중 하나로 평가되고 있다(Kim and Lee, 2002; Lee et al., 2007; Liu et al., 2008; Nam et al., 2010; Park et al., 2010; Seo et al., 2010; Park and Jung, 2012; Jung et al., 2011; Jeong et al., 2013; Kim et al., 2013).
일반적으로 VOF법은 유체의 체적비율(Volume fraction)을 활용하여 유체의 경계면(Interface)을 나타낼 때 크게 두 가지 접근법으로 분류될 수 있다. 그 하나는 유체의 경계면을 주어진 체적비율에 따라 기하학적으로 재구성(Geometric reconstruction)하는 알고리즘으로 재현하고 Lagrangian개념으로 그 움직임을 추적하는 계면추적법(Interface tracking method) 계열이다. 가장 잘 알려진 대표적인 방법으로 SLIC(Simple line interface calculation, Noh and Woodward, 1976), Hirt and Nichols(1981)의 VOF 그리고 PLIC(Piecewise line interface calculation, Young, 1987)이 있다. 이 후 비슷한 개념을 바탕으로 다수의 확장된 방법들이 개발되었으며 다소 최근에 개발된 고차 정도의 기법을 일례로 들자면 MOF(Moment of fluid, Ahn and Shashkov, 2009)법을 소개할 수 있다. 한편으로, 이 계열의 방법들 중 2차 정도 이상의 기법들은 그 정확도에 대비되어 알고리즘이 복잡하기 때문에 다양한 격자에 대한 적용성 및 3차원 확장성이 상대적으로 어려운 것으로 알려져 있다(Ubbink and Issay 1999). 계면추적법에 대비된 다른 개념의 VOF법은 계면포착법(Interface capturing method)으로 분류되며 유체의 체적비율을 함수로 취급하고 이를 고차 차분법(High resolution differencing scheme)으로 추정하고 이송하는 방법이다. 이 접근법의 전략은 질량보존 특성을 만족하기 위해 사용하는 상류차분법(Upwind differencing scheme)과 정확한 유체 경계면 포착을 위해 도입하는 하류차분법(Downwind differencing scheme)을 적절한 방법으로 혼합하여 새로운 차분법을 개발하는 것이다. 대표적으로 널리 사용되는 방법은 HRIC (High resolution interface captureing, Muzaferija et al. 1998), CICSAM(Compressive interface capturing scheme for arbitrary meshes, Ubbink and Issay 1999) 그리고 MHRIC(Modified HRIC, Fluent 2006)이다. 이러한 계면포착 개념의 기법들은 앞서 열거한 사례에서 조선해양공학 문제에 적용되고 있는 VOF법들의 대부분을 차지하고 있는데, 이는 알고리즘의 복잡성 정도, 계산시간, 문제에서 요구되는 정확도 수준 그리고 다양한 격자 조건 및 문제에 대한 강건성(Robustness) 등을 고려할 때 상대적인 이점이 많기 때문이다.
본 논문에서 다루고자 하는 표면장력의 영향을 고려해야하는 유동문제에서 VOF법은 유체 경계면을 통한 체적비율의 불연속적 특성을 가지기 때문에 이 값을 그대로 이용하여 경계면의 법선 벡터 및 곡률을 계산할 경우 부정확한 결과를 얻을 수 있다. 최근 이러한 문제를 해결하기 위해 질량보존 특성이 우수한 VOF법과 유체 경계면의 기하학적 특성을 계산하는데 적합한 LS법(Level-set method)을 엄밀한 접목 알고리즘으로 혼합하는 수치 해석법들이 개발되고 있다(Son, 2003; Sussman et al., 2007). 본 논문에서는 계면포착법 개념의 VOF법을 이용하고 유체 경계면의 법선벡터 및 곡률 계산의 정확도를 개선하기 위해 LS법을 직접적이고 보다 용이한 접근법으로 접목하는 새로운 수치 해석법을 소개한다. 본 방법은 복잡한 알고리즘이 필요한 엄밀한 연성(Coupling)은 피하고 타당한 정확도의 해를 얻으면서 계산의 효율을 높이는데 목적을 두고 있다. 수치해석 결과에서는 밀도차가 큰 유동장의 3차원 단일기포 상승 문제를 다루고 격자 수렴성 검토 및 타 연구 결과와의 비교를 통해 본 수치 해석법의 정도를 검증하였다.
본 논문에서 사용된 이상유동에 대한 지배방정식으로 비압축성 (Incompressible) Navier-Stokes 방정식과 연속방정식(Continuity equation)의 적분표현은 다음과 같이 쓸 수 있다.
여기서 𝛺는
지배방정식은 유한체적법(Finite volume method)으로 이산화하였다. 시간적분은 2차 정도의 Three-time-level법(Ferziger and Perić, 1996)으로 수행되며, 대류항과 확산항에 대한 이산화는 3차 정도의 MUSCL(Monotonic upstream centered scheme for convection laws, van Leer, 1979)법과 2차 정도의 중심차분법(Central differencing scheme)으로 수행하였다. 연속방정식은 SIMPLE (Patankar, 1980)알고리즘을 이용하여 만족시켰다.
두 유체의 경계면은 유동장에서 각 유체가 차지하는 체적비율로 모델링할 수 있으며 다음의 이송방정식(Transport equation)을 풀어 그 움직임을 구할 수 있다.
여기서, 𝛼는 체적비율로서 액체 영역에서 1, 기체 영역에서 0, 두 유체의 경계면에서 0 <𝛼 <1의 값을 갖는다.
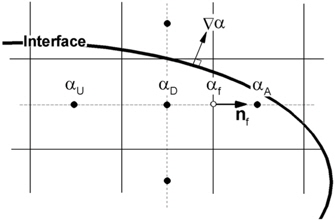
본 논문에서는 대표적인 계면포착법 개념의 VOF법인 HRIC, MHRIC 그리고 CICSAM에서 사용하는 차분법 개념을 도입하고 기존 HRIC와 MHRIC의 정도를 개선한 RHRIC(Refined HRIC, Park et al. 2010)를 사용하였다. 다음은 RHRIC에서 도입된 방법으로서 상류차분법과 하류차분법을 적절히 혼합하여 식 (3)을 풀기위해 필요한 격자요소 경계면을 통한 𝛼
여기서, 아래첨자
여기서,
여기서, 는 격자 경계면에서의 질량유량이고, Δ
최종적으로 RHRIC는 상기 상류차분법과 하류차분법을 혼합하여 격자의 경계면에서 정규화된 체적비율 𝛼
여기서, 𝛾
유체 경계면의 표면장력의 영향은 다음과 같은 CSF모델 (Continuum surface force model, Brackbill et al., 1992)을 이용하여 운동량방정식에 고려할 수 있다.
여기서, 𝜎는 표면장력 계수이고 𝜅는 유체 경계면의 곡률을 나타낸다. 식 (13)의
본 논문에서는 계산시간을 위해 VOF법과 병행하여 LS법의 이송방정식을 별도로 풀지 않고 VOF법에서 얻어진 해를 바탕으로 유체 경계면을 영점으로 한 주위 근방 영역의 각 위치에서의 거리함수 분포를 구하는 방법을 도입하였다. 이 때 일반적으로 LS법에서 이송방정식을 풀고 난 후 부정확하게 변한 거리함수 분포를 수정하기 위해 사용되는 아래와 같은 비선형 쌍곡선 미분방정식 형태의 재초기화(Reinitialization) 방정식을 도입하였다(Sussman et al., 1997).
여기서, 𝜏는 방정식을 풀기 위한 가상의 시간이며 𝜙𝛼는 식 (14)에 주어지는 초기조건으로 VOF법에서 구한 유체 경계면(𝛼=0.5)을 포함한 주위 체적비율 정보를 거리함수로 다음의 식을 통해 변화시킨 값이다.
여기서, 𝞊은 수치해석에서 필요한 유체 경계면의 두께를 나타내고 본 논문에서는 𝞊 =2Δ
여기서,
재초기화 방정식 (14)는 시간 적분법으로 1차 정도의 Euler법을 사용하고 우변의 대류항은 5차 정도의 WENO법(Weighted essentially non-oscillatory scheme)을 이용하여 풀었다. 5차 정도의 WENO법은 다른 ENO계열보다 질량보존 특성이 우수하고 주어진 유체 경계면의 원래 위치를 손상시킬 수 있는 수치 번짐(Numerical smearing)의 영향이 적은 것으로 알려져 있다. 이에 대한 검증 결과와 복잡한 수식 전개 결과는 Croce et al.(2004)의 자료에서 참고할 수 있다.
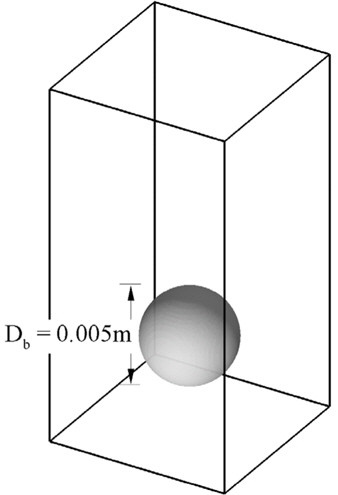
본 논문에서 제시하는 수치기법의 검증을 위해 점성은 물론 밀도의 차가 1:1000인 3차원 기포 운동 계산을 수행하였다. 초기 정지해 있는 상태의 기포를 포함한 유동장의 그림은 Fig. 2에서 볼 수 있으며, 여기서, 기포의 직경은 0.005
본 수치기법의 격자 민감도를 검토하기 위해 coarse(35×35×70), medium(50×50×100), fine(70×70×140)의 균등 분포를 가지는 세 가지 직교격자(Cartesian grid)를 생성하였다. 생성된 직교격자들의 내부 절점 간격과 격자 수는 각 격자 간 배의 비율로 변한다. 수치계산은 Fig. 2와 같이 초기 정지 상태로부터 시작하고 검증을 위해 필요한 데이터로서 매시간 기포의 수평방향의 최대 직경(
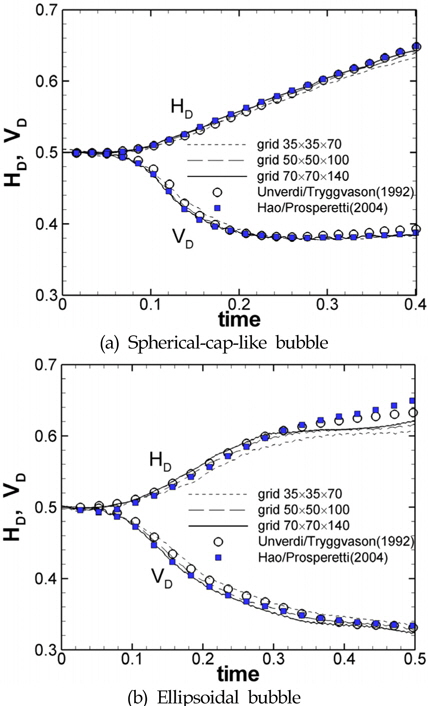
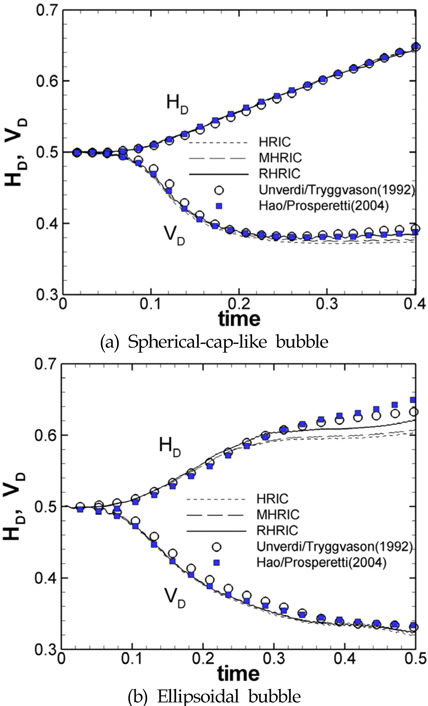
Fig. 3은 두 가지 조건의 표면장력 계수 값에 따른 기포의 수평 및 수직방향 최대 직경들의 시간 변화를 비교하고 있다. Unverdi and Tryggvason(1992)과 Hao and Prosperetti(2004)의 수치해석 결과들은 이전 절에서 간단히 설명한 바와 같이 유체의 경계면인 기포를 표면격자로 구성하여 그 변형과 운동을 직접적으로 추적하는 방법으로 얻은 결과들이다. 표면장력의 영향이 크지 않고 이와 관련된 수치오차가 작을 것으로 예상되는 구형-모자형태 기포 상승 문제에 대한 비교 결과인 Fig. 3-(a)에서 격자 변화에 따른 본 수치해석의 결과들이 Unverdi and Tryggvason(1992)과 Hao and Prosperetti(2004)의 수치해석 결과들과 좋은 일치를 보여주고 있다. Fig. 3-(b)에서는 높은 표면장력 계수에 대한 타원형태의 기포 상승 문제의 결과들이 격자 및 수치해석법들 사이에서 표면장력의 영향이 작은 앞선 결과보다 다소 차이를 보여주고 있다. 표면장력 영향이 커지면서 격자의 민감도가 다소 높아지는 것을 볼 수 있으며, 타 연구결과에서 표면장력을 운동량방정식에 고려하는 수치기법 차이와 기포를 구성하는 표면격자의 수 등에 의한 세밀한 수치적 차이들이 Fig. 3-(b)에 나타나는 차이를 만든 것으로 보인다. 이와 같이 수치 해석적 차이에서 기인된 Fig. 3-(b)에 보이는 세밀한 차이가 존재하지만, 본 수치해석 결과는 전반적으로 높은 밀도차와 표면장력 영향에 대해 비교적 만족할만한 타당한 해를 제공하는 것으로 판단된다.
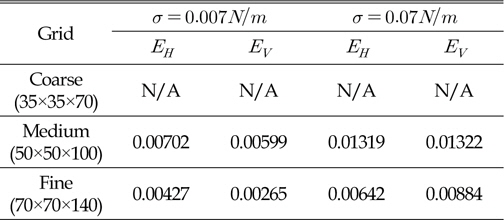
Table 1은 격자 수렴성을 수치화하여 보다 구체적으로 검토하기 위해 Fig. 3의 격자에 따른 수평방향 및 수직방향의 최대 직경에 대한 시간 변화 결과를 다음 식에 대입하여 격자 간 수렴오차를 각각 구한 값을 보여주고 있다.
[Table 1] Relative errors between succeeding grids
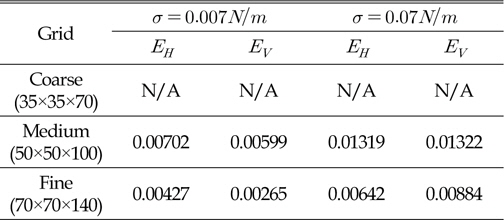
Relative errors between succeeding grids
여기서, 아래첨자 1과 2는 연속된 두 격자를 나타낸다. Fig. 3의 비교에서 볼 수 있었듯이 표면장력의 영향이 큰 경우 격자 간상대 오차가 다소 증가된 것을 볼 수 있다. 그러나 결과적으로 두 시뮬레이션 조건에 대해 본 논문에서 제시하는 수치해석 기법은 coarse와 medium간의 오차보다 medium과 fine격자 간의 오차가 작은 단조 수렴하는 특징을 잘 보여주고 있다.
Fig. 4는
Fig. 5는 x-z면에서 기포 경계면 주위 VOF법의 체적비율
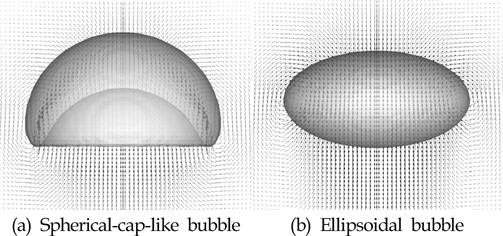
Fig. 6은 본 수치기법으로 계산된 3차원 기포의 모양과 겹쳐 x-z평면에서의 기포 내부영영과 그 주위 유동장의 속도벡터 분포를 보여주고 있다.
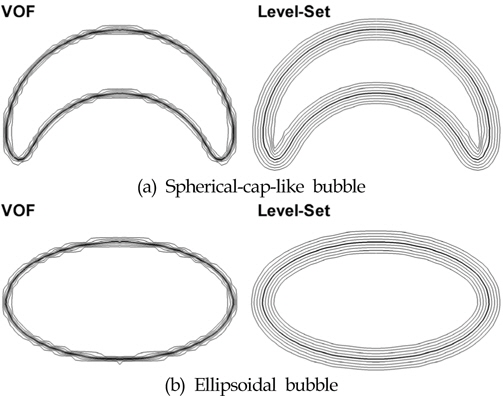
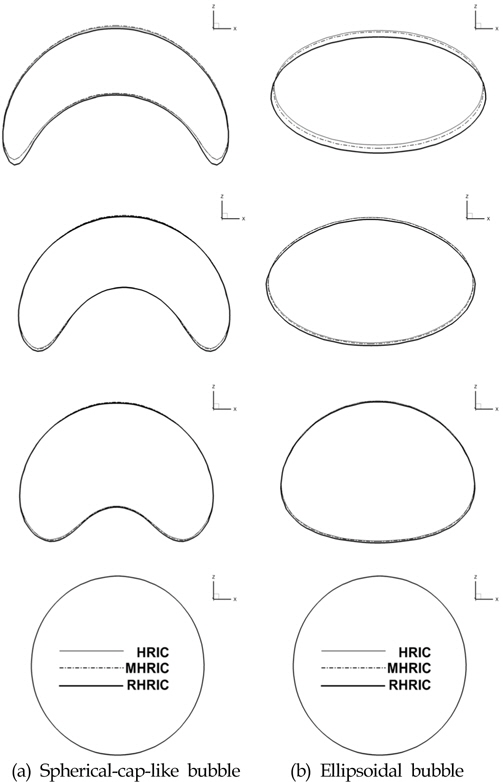
Fig. 7은 HRIC, MHRIC 그리고 본 방법인 RHRIC의 세 가지 VOF법으로 계산한 상승하는 기포의 수평 및 수직방향 최대 직경들의 시간 변화를 비교하고 있다. Fig. 7-(a)는 표면장력의 영향이 작은 경우로서 수평방향의 최대 직경의 차이는 거의 무시할 정도로 동일하며 수직방향의 직경의 변화가 미미하게 나타고 있지만 대체로 세 가지 방법이 거의 동일한 결과를 보여주고 있다. 이러한 결과는 Fig. 8-(a)에 제공된 그림에서 x-z평면에서의 시간에 따른 기포의 위치를 포함한 윤곽선(Profile) 비교에서도 동일하게 볼 수 있다. 정확하게는 시간의 경과에 따라 본 수치기법의 결과가 타 수치해석 결과와 어느 정도 더 근접하다고 말할 수 있다. 표면장력의 영향이 큰 Fig. 7-(b)의 비교 결과에서는 세 VOF법 간에 다소 서로 다른 차이를 보이고 있다. 수평방향의 최대 직경에 대한 시간변화의 경우 RHRIC의 경우가 타 수치기법의 결과와 더 잘 일치하고 HRIC와 MHRIC의 경우 시간의 경과에 따라 기포의 크기를 다소 작게 예측하고 있다. 이러한 경향은 Fig. 8-(b)의 그림에서 다시 확인할 수 있다. 수직방향의 크기에 대해서는 거의 비슷한 결과를 보이고 있지만, Fig. 8-(b)를 보면 기포의 수직방향 위치가 서로 다른 것을 볼 수 있다. 여기서, 기포의 수직 위치 차이는 시간이 흐를수록 더 커지는 것을 그림에서 확인할 수 있다. 작은 차이이지만 비슷한 경향이 표면장력의 영향이 작은 결과에서도 나타나고 있다. 결과적으로 본 논문에서 사용한 RHRIC기법이 Unverdi and Tryggvason(1992)과 Hao and Prosperetti(2004)의 수치기법의 결과에 더 근접한 일치를 보여준다고 할 수 있는데, 이는 Park et al. (2010)의 논문에서 볼 수 있듯이 각 VOF법이 가지는 질량보존 정도에 기인된 결과로 판단된다.
본 논문에서는 표면장력 영향을 고려한 비압축성 이상유동을 해석하기 위해 VOF법과 LS법을 접목한 새로운 수치기법을 소개하였다. 본 수치기법은 표면장력 계산에 필요한 유체 경계면의 법선벡터와 곡률의 계산 정확도를 개선하기 위해 VOF법에서 얻어진 해를 초기조건으로 사용하여 LS법의 재초기화 방정식을 풀고 여기서 구한 부드러운 연속함수인 LS함수 분포를 이용한다. 본 논문의 접근법은 복잡한 알고리즘이 필요한 VOF법과 LS법 사이의 엄밀한 연성은 피하고 비교적 타당한 정확도의 해를 얻을 수 있는 계산의 효율에 목적을 두고 있다. 검증을 위해 두 가지 표면장력 계수 조건을 가지는 점성과 밀도 차이가 큰 이상유동장 내 3차원 기포 상승 문제에 본 방법을 적용하였다. 수치해석 결과에서 본 수치기법은 각각의 해석 조건에 대해 모두 단조 수렴하는 격자 의존성 특징을 잘 보여주었으며, 다른 두 가지 접근 방법으로 구한 타 수치기법의 결과와도 비교적 좋은 일치를 보여주었다. 동일한 문제에 대해 HRIC와 MHRIC VOF법을 적용하여 그 결과를 비교하였으며 표면장력의 영향이 큰 시뮬레이션 조건에서 RHRIC법이 두 방법보다 타 수치해석 결과와 더 근접한 일치를 보였다. 향후 관련된 다양한 문제에 대해 본 방법을 검증할 필요가 있으며 해석 정도의 향상을 위해 표면장력 영향을 보다 정확히 모델링 할 수 있는 수치기법을 검토하여 고려해야 할 것으로 판단된다.