The effect of the third-body perturbation is one of the most important mechanisms in delivering the major Earth orbiting objects into the regions where the atmosphere starts to decay. Several papers have studied the third-body perturbation of the Sun and the Moon on a satellite orbiting the Earth and major related works are listed as follows. In a series of papers (Kozai 1959, 1962, 1965), Kozai developed the secular and long period terms of the disturbing function due to lunisolar perturbations in terms of the orbital elements of a satellite, the Sun and the Moon, and applied those secular perturbations to asteroids with high inclination and eccentricity assuming that Jupiter is the perturbing body. Blitzer (1959) obtained the estimates of secular terms due to lunisolar disturbances. In the sequence, Cook (1962) used the Lagrange’s planetary equations to obtain expressions for the variations of elements during the revolution of a satellite and for the rates of variation of the elements. Giacaglia (1974) obtained the disturbing function for the disturbance of the Moon using the ecliptic elements for the Moon and the equatorial elements for a satellite. Hough (1981) studied the effects of lunisolar disturbances in orbits close to critical inclinations from the point of view of the geopotential of the Earth and concluded that the effects are significant in high altitudes. Broucke (2003) and Prado & Costa (1998), truncated the disturbing function of the third body after the second and the fourth order expansion in Legendre polynomials, respectively. After that, Costa (1998) expanded the order of this model to the eighth order. Solόrzano & Prado (2007) developed a semi-analytical study of the perturbation caused on a spacecraft by a third body with a single averaged model to eliminate the terms due to the short-lived periodic motion of the spacecraft. Prado (2003) studied the evolution of retrograde orbits around the Earth. The existence of circular, equatorial and frozen orbits was also considered. Costa & Prado (2002) discussed the critical angle of a third-body perturbation that is a value for the inclination such that any near-circular orbit with inclination below this value remains near- circular. Domingos et al. (2008) showed an analytical expansion to study the third-body perturbation for a case where the perturbing body is in an elliptical orbit, based on the expansion of the perturbing function in polynomials of Legendre.

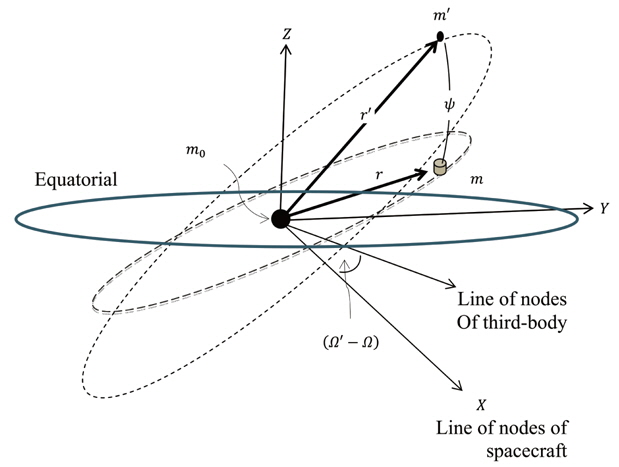
In this paper, the study done by Broucke (2003), Prado (2003) and Domingos et al. (2008) is expanded, including the eccentricity and inclination of the perturbing body. A three-dimensional model is used to study the effects of a third-body gravitational potential on the spacecraft that orbits near a celestial body including the eccentricity and the inclination of the third-body in the formulation. There is no assumption in our study on the perturbed and perturbing orbits except the usual assumption that there are only three bodies involved in the system: the first body with mass, m₀, fixed at the origin of the reference. The doubleaverage is taken over the mean motion of the spacecraft and that of the disturbing body after expansion of the disturbing function in Legendre polynomials.

This paper is organized as follows. In Section 2, we formulate the disturbing function (using the traditional expansion in Legendre polynomials) due to a third body truncated up to the second-order term. In Section 3, The Lagrange’s planetary equations for the variations of spacecraft’s orbital elements are shown. In Section 4, we simulate the study assuming a spacecraft in an elliptical inclined orbit around the Moon with its motion perturbed by the Earth.

About notations through this paper, we use the wellknown Keplerian elements: the semi-major axis, a, the eccentricity, e, the inclination, i, the right ascension of ascending node, Ω, the argument of periapsis, w, f is the true anomaly and the mean anomaly, M. Also, the same notations with prime will be used for the third body. It is assumed that the main body with mass m₀ is fixed in the center of the reference system. The perturbing body, with mass m' is in an elliptic inclined orbit with mean motion n', given by the expression n'²a'³=g(m₀+m'), where r and r' are the radius vectors of the spacecraft and m' (assuming r'»r₀ ), and ψ is the angle between these radius vectors. The disturbing function (using the traditional expansion in Legendre polynomials; P_n) due to the third body is given by

where g is the gravitational constant and ψ is the angle between the line that connects the massive central body and the perturbed body (the spacecraft) and the line that connects the massive central body and the perturbing body (the third body).

For the models used in this research, it is necessary to calculate the parts of the disturbing function due to R₂,

The magnitude of the effect of the disturbing body on the orbit of a spacecraft depends on the position of the disturbing body in its orbit. The next step is to express cos ψ in terms of the orbital elements. It is clear from Fig. 1 that the base vectors along and may be defined as

where r and r' are the moduli of vectors and from which

where u=f+ω is usually known as the argument of latitude and ΔΩ=Ω'-Ω is the difference of the nodal longitudes. In the subsequent developments the adopted reference frame is an equatorial system with the positive X-axis towards the node of the orbit of m, Z-axis towards the north pole of the equator of the primary, and the Y-axis completing a right handed system.

The last relation can be rewritten in a compact form as below:

where the non-vanishing coefficients are

The next step is to average expression (2), using Eq. (3), over the short period of the spacecraft as well as with respect to the distant perturbing body. The standard definition for the average can be written as:

This yields

Rewriting above equation gives

where the non-vanishing coefficients are

Using Lagrange planetary equations, the variation of the orbital elements due to the averaging disturbing potential «R₂» is established as, e.g. Brouwer & Clemence (1961):

where

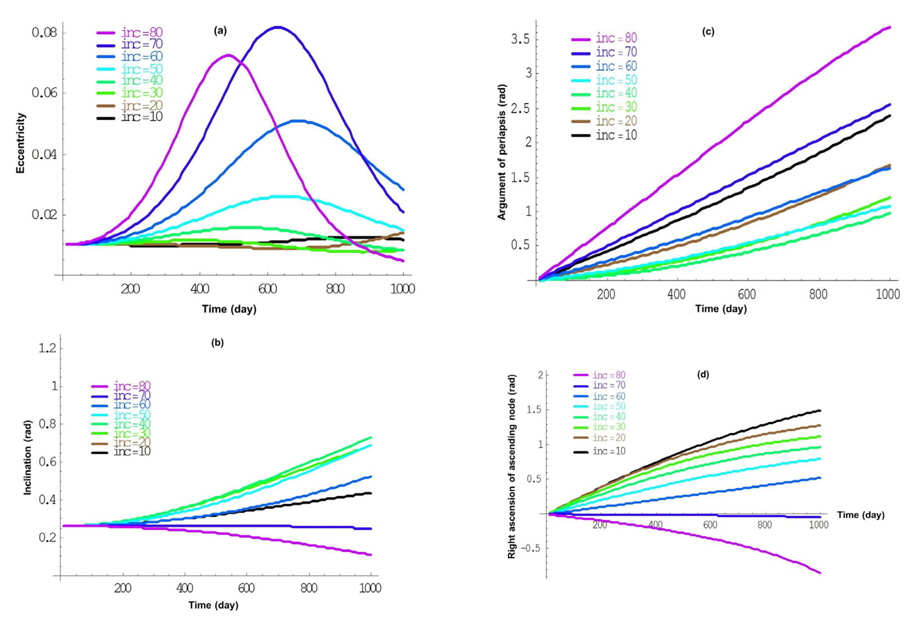
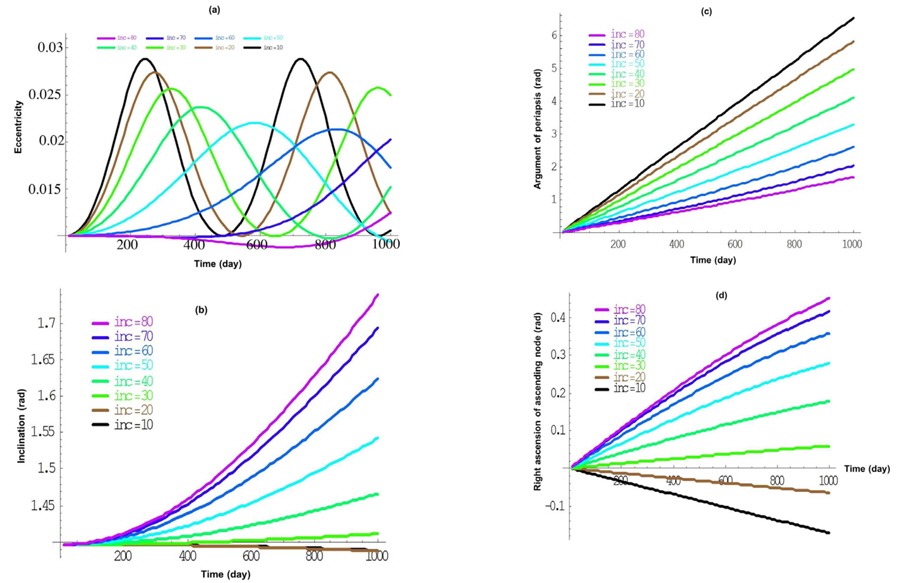
In this section, we suppose a spacecraft in an elliptical inclined orbit around the Moon and its motion perturbed by the Earth for a duration time of 1,000 days. The initial conditions found in Prado (2003) and Domingos et al. (2008) ; a lunar satellite with a₀=0.01 (3,844km), e₀=0.01, i₀=15°,60° and ω₀=Ω₀=0°were used to show the behavior of the evolutions of the spacecraft orbital elements with time. The perturbing body was in elliptical (e'=0.1) inclined ( 10°≤i'≤80°). From the graphs shown in Fig. 2 and Fig. 3, it is revealed that the evolutions of argument of pericenter (ω) keeps increasing for a fixed third body's inclination (i') but as (i') goes to higher angle, the rate of increase in ω gets lower. On another hand, the evolutions of right ascension of the ascending node (Ω) and inclination (i) keep decreasing with fixed i' up to the certain angle but as i' changes upward, they increase while the rate of increase in Ω and i decreases. The evolution eccentricity (e) shows periodical behavior with the time even if the amplitude depends strongly on the (i').

Beginning this study, the basic question is; what is the effect of inclined third body on the spacecraft orbital elements? For the answer, the effects of wide range of the inclinations of the third body (10°-80°) are presented. Using the initial conditions found in Prado (2003) and Domingos et al. (2008), the results of changing the third body’s inclinations over (10°-80°) on the model indicated that the effect of the third body’s inclinations cannot be neglected to be consistent with many previous studies.

In this paper, we have used three-dimensional model to analyze the perturbations of the third body potential on a spacecraft that orbits close to a heavenly body including the eccentricity and the inclination of the third-body of the perturbing body within the formulation.

All curves turned out to be smooth through the well-known double-average model based on the mean motion of the spacecraft and the perturbing body which plays an important role in the analysis of spacecrafts long term dynamics enabling the short-lived periodic terms to be eliminated.