This paper presents an extensive experimental comparison of a variety of multi-label learning methods for the accurate prediction of subcellular localization of proteins which simultaneously exist at multiple subcellular locations. We compared several methods from three categories of multi-label classification algorithms: algorithm adaptation, problem transformation, and meta learning. Experimental results are analyzed using 12 multi-label evaluation measures to assess the behavior of the methods from a variety of view-points. We also use a new summarization measure to find the best performing method. Experimental results show that the best performing methods are power-set method pruning a infrequently occurring subsets of labels and classifier chains modeling relevant labels with an additional feature. futhermore, ensembles of many classifiers of these methods enhance the performance further. The recommendation from this study is that the correlation of subcellular locations is an effective clue for classification, this is because the subcellular locations of proteins performing certain biological function are not independent but correlated.
단백질은 생명체내에서 효소, 영양 저장, 호르몬, 운동, 면역, 정보교환, 구조형성 등의 많은 기능을 수행한다. 동물, 식물, 곰팡이와 같은 진핵생물은 세포 내부의 정교한 구획과 세포소기관이 존재하는데, 이들 지역은 서로 다른 생화학적 환경이 생겨 세포내 위치에 따라 특정한 대사 기능을 수행한다. 따라서 단백질의 기능을 알기 위한 기초 지식은 단백질이 존재하는 세포내의 위치를 알아내는 것이다. 단백질의 세포내 위치를 예측하는 많은 연구들은 오직 하나의 세포내 위치에 존재하는 단백질만을 대상으로 하였지만, 여러 세포내 위치에 동시에 존재하는 단백질의 생물학적 기능이 중요하므로, 이를 예측하려는 시도가 커지고 있다[1-8]. 다중 세포내 위치 예측은 하나의 단백질에 대해 세포내 위치를 나타내는 레이블 집합의 부분집합을 예측하는 다중레이블 분류문제이다. 세포내 위치 개수
다중 세포내 위치 예측에 적용할 수 있는 기계학습방법인 다중레이블 분류 방법은 최근 들어 활발히 연구 되고 있다[9-11]. 이는 이미지, 비디오, 텍스트, 음악, 마케팅, 생물학 분야에서 하나의 입력 자료에 대해 여러 가지 분류에 동시에 속하는 상황이 발생하기 때문이다. 다중레이블 분류 방법을 (1)알고리즘 적응, (2)문제 변환, (3)메타 학습으로 나누어 볼 수 있다[9-11]. 알고리즘 적응 방법은 기존의 단일 분류 알고리즘인 최근접-이웃 분류기, 신경망, 결정 트리, 지지 벡터 기계를 다중레이블에 맞도록 변형한 방법이다. 문제 변환 방법은 다중레이블 분류문제를 다수의 단일레이블 분류문제로 변환한 후에 단일레이블 분류 알고리즘을 적용하는 방법이다. 메타 학습 방법은 알고리즘 적응방법이나 문제 변환 방법의 여러 개를 동시에 적용하여 조합하여 분류기를 구성하는 방법이다.
다중레이블 분류를 이용하여 단백질의 세포내 위치를 예측 방법들을 살펴보면, 최근접-이웃 분류기의 앙상블을 사용하는 방법[1, 7], 가우시안 과정 모델과 공분산 행렬로 레이블간의 연관성을 표현하는 방법[3]이 있다. 문제 변환 방법을 사용하는 예로, 세포내 위치의 모든 쌍들에 대한 분류기를 구성하여 투표하여 최종 결과를 얻는 방법[2]과 특정 레이블에 관련된 사례들과 관련되지 않은 사례들로 학습하는 BR(binary relevance)을 사용하는 방법[4,6]이 있다. 또한,
최근에 개발된 다양한 다중레이블 분류 방법이 단백질의 다중 세포내 위치 예측의 적용을 위하여 충분히 비교 분석되지 않았다. 본 논문에서는 광범위한 다중레이블 분류 방법의 비교를 통하여, 단백질 세포내 위치 예측에 효과적인 방법을 알아내고, 그 방법들의 특징을 분석한다. 또한, 다중레이블 분류의 복잡한 예측결과를 다양한 측면에서 살펴보기 위하여 12개의 평가 척도를 사용하고, 새로운 요약 척도를 사용하여 최적의 방법들을 찾는다.
단백질 세포내 위치 예측에 효과적인 방법을 찾고자 다중레이블 분류 방법을 알아본다. 다중레이블 분류는 사례(example)와 관련된 다중 레이블을 찾는다. 즉, 레이블들의 집합을
이번 장에서는 IV장의 비교 실험에 사용되는 다중레이블 분류 알고리즘을 중심으로 하여 (1)알고리즘 적응, (2)문제 변환, (3)메타 학습으로 나누어 살펴 본다[9-11]. 알고리즘 적응 방법은 단일레이블 분류 알고리즘인 최근접-이웃 분류기, 트리 분류, 신경망, 지지 벡터 기계 등을 다중레이블 분류에 적합하도록 확장하거나 변형한다. Ml-knn의 경우에는 각 사례에 제일 근접하는 이웃을 찾고, 평가 자료의 레이블집합을 결정하는 과정에서 각 레이블에 대하여 k 개의 최근접 이웃의 사전확률과 사후확률을 사용한다[12]. BRkNN도 최근접-이웃 분류기를 사용하고, 다중레이블 분류문제를 아래에 설명할 문제 변환인 BR(binary relevance)을 사용한다[13]. IBLR_ML은 로지스틱 회귀와 최근접-이웃 분류기를 결합한 방법이다[14]. BPMLL은 기존의 역전파 학습을 사용한 신경망을 다중레이블 분류를 고려하여 새로운 오류 함수를 도입한 방법이다[15].
문제 변환 방법은 다중레이블 분류를 다수의 단일레이블 분류로 바꾸는데, BR(binary relevance), LP(label power-set)와 PW(pair-wise)로 나누어 볼 수 있다[9-11]. BR은 각 레이블에 관련된 사례로 양성 집합(positive set), 이외의 사례로 음성 집합(negative set)을 구성하여 학습하고, 각 레이블에 해당하는 분류기의 결과를 조합한다. CC(classifier chains)는 BR과 유사한 방법으로
메타 방법은 여러 다중 레이블 분류기를 배깅(bagging), 부스팅(boosting)과 스태킹(stacking)을 사용하여 조합한다. 배깅은 동일한 종류의 여러 분류기를 조합하는 방법으로 투표를 사용 하는 경우에 각 방법에 동일한 가중치를 부여한다. ECC(ensemble of classifier chains) 와 EPS(ensemble of pruned sets)는 각각 CC[16]와 PS[17]로 다수의 분류기의 구성하는 배깅 방법이다. HOMMER는 여러 레이블들 간의 계층적 관계를 구성하고, 각 계층에서 분류기를 구성하는 방법이다. 각 분류기는
다중레이블 분류기에 대한 성능 평가는 기존의 단일레이블 분류기에 사용되는 성능 척도를 그대로 사용할 수 없다. 즉, 예측된 레이블이 실제 레이블과 일치하는 것만을 판단하면 지나치게 엄격한 평가 척도가 되므로, 일부만 일치하는 경우도 고려한다. 따라서 여러 관점에서 예측 정확도를 판정할 수 있는 방법들이 사용되고 사례기반(example-based)과 레이블기반(label-based)으로 나눈다[9-11]. 식 (1)~(6)의 사례기반 방법은 각 사례에 대해 실제 레이블과 예측된 레이블간의 차이를 평균하고, 식 (7)~(12)의 레이블기반 방법은 각 레이블에 대해 개별적으로 예측성능을 구하고 이를 평균한다.
사례
다음에 설명할 척도들은 값이 클수록 정확한 예측이다.
본 연구에서는 식 (1)~(12)의 많은 평가 척도를 사용하므로 각 방법의 비교가 쉽지 않다. 이를 요약하기 위한 새로운 척도로서 합계를 구하는데,
단백질의 세포내 위치 예측에 효과적인 다중레이블 분류방법을 찾기 위해 비교 하였다. 실험에 사용한 자료는 인간 단백질 자료로 세포내 위치는 14개(centriole, cytoplasm, cytoskeleton, endoplasmic reticulum, endosome, extracell, golgi apparatus, lysosome, microsome, mitochondrion, nucleus, peroxisome, plasma membrane, synapse)이고, 2,580개의 단백질은 하나의 세포내 위치, 480개는 두 개의 위치, 43개는 3개의 위치, 3개는 4개의 위치에 존재한다[1]. 단백질 서열들은 25% 이하의 작은 서열 동일성을 가지고 있으므로, 서열 유사성만을 이용하여 단백질의 세포내 위치를 예측하기는 어려운 자료이다.
비교 실험에는 5겹 교차검증을 수행하기 위해서 실험 자료를 균등하게 5개로 나누어 사용하였다. 단백질 자료를 다중레이블 분류를 위한 특징 벡터로 변환하기 위해서 논문[1,2,4-7]처럼, 유전자 온톨로지를 가진 데이터베이스(http://www.ebi.ac.uk/GOA)를 탐색하여 주어진 단백질 자료와 가장 유사한 단백질의 유전자 온톨로지를 사용하였다. 유전자 온톨로지는 분자적 기능, 생물학적 과정, 세포 요소의 관점에서 특징화한 용어로 유전자를 표현한 것으로, 유전자 해당하는 단백질의 특징을 나타낸다.
다중레이블 분류기는 Mulan 라이브러리로 구현하였고, 기본 설정을 사용하였다[9]. 각 방법의 성능은 III장의 평가척도 식(1)~(12)로 측정하였고, 비교를 위해 간략한 척도
표 1은 II장에서 설명한 알고리즘 적응 방법의 실험 결과이다. 알고리즘 적응 방법은 이후의 비교 방법들보다 성능이 저조하므로, 다중레이블 분류를 위해서 보다 개선된 알고리즘의 확장이 필요하다.

알고리즘 적응 방법의 성능 비교
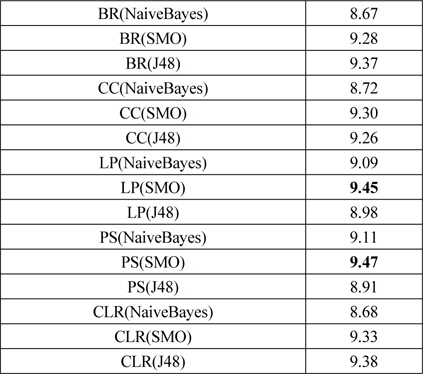
문제 변환 방법은 다중레이블 분류문제를 다수의 단일레이블 분류문제로 변환하고 단일레이블 분류를 하므로, 단일 분류 방법이 필요하다. 이를 위해 기본적인 문제 변환 방법인 BR에 대해서 단일 분류 방법들을 비교하여 우수한 단일 분류기를 이후에 사용하였다. Mulan 라이브러리가 기반한 Weka[24]에서 베이즈 분류기 (NaiveBayes, NaiveBayesMultinomial), 지지 벡터 기계 (SGD, SMO), 예제 기반 lazy 분류기(IBk, KStar, LWL), 신경망(MultilayerPerceptron), 트리 기반 분류기(J48, LMT, RandomForest, REPTree)를 비교하였다. 베이즈 분류기에서는 NaiveBayes, 지지 벡터 기계에서는 SMO, 트리 기반 분류기에서는 J48 방법이 우수하였다. 예제기반 lazy 분류기는 성능이 저조하고, 신경망은 실험 시간이 오래 걸려서 문제 변환 방법에 적용하기 어려웠다. 표 2는 문제 변환 방법의 성능이고, 괄호 안에 사용한 단일 분류 방법을 표시하였다.
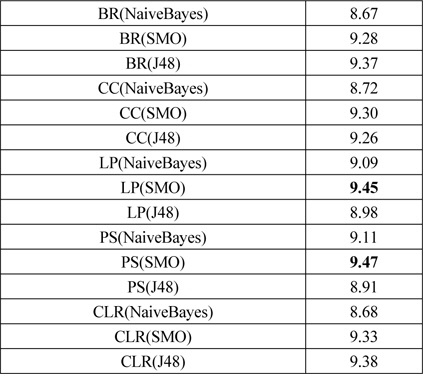
문제 변환 방법의 성능 비교
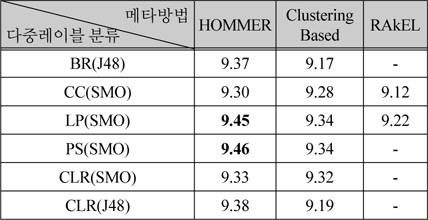
메타 방법 중에서 HOMMER, ClusteringBased, RAkEL은 다중레이블 분류기를 조합하는 방법이다. 표 1과 표 2에서 성능이 9.3 이상인 BR(J48), CC(SMO), LP(SMO), PS(SMO), CLR(SMO), CLR(J48)에 대하여 조합한 결과를 표 3에 나타내었다. 표 3에서 - 표시는 메모리 부족으로 실행 실패를 나타낸다. 본 논문에서는 16 기가바이트의 메모리를 사용하였고, 5겹 교차 검증을 병렬로 수행하였다.
[표 3.] 다중레이블 방법을 조합한 메타방법의 성능 비교
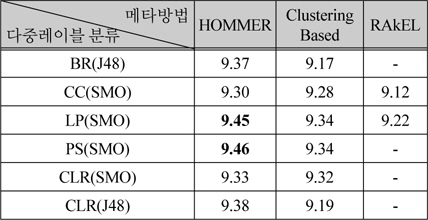
다중레이블 방법을 조합한 메타방법의 성능 비교
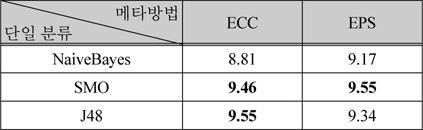
표 4는 메타 방법 중에서 배깅을 사용하는 방법인 ECC와 EPS의 결과이다. 이 방법들에서도 단일분류로 NaiveBayes, SMO, J48을 적용하였다.
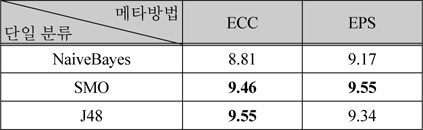
배깅을 사용한 메타방법의 성능 비교
메타 방법에서 부스팅을 사용하는 AdaBoostMH는
비교실험한 모든 다중레이블 분류 방법에서 성능이 9.4이상인 방법들에서 대해서, 부가적으로 단백질의 특징을 보다 효과적으로 표현하면 분류 성능이 향상되는지를 실험하였다. 카이제곱 검정값을 변형하여 단백질의 세포내 위치를 판별력이 높게 나타내는 유전자 온톨로지 가중하는 방법을 적용하였다[25]. 원래의 방법이 가장 유사한 서열의 유전자 온톨로지만을 사용하는 것에 반하여, 본 연구에서는 가장 유사한 두 개의 서열에서 나타나는 유전자 온톨로지의 빈도를 이용하였다.
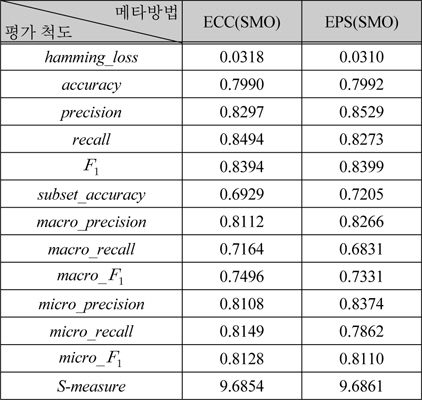
표 6은 표 5에서 성능이 가장 높은 ECC(SMO)와 EPS(SMO)를 식 (1) ~ (12)의 평가 척도로 다양한 관점의 성능을 보여준다. 표 6의 두 가지 방법은 전체적인 성능은 유사하지만, precision, recall이 상반된 값을 갖는다. 이러한 경향은 레이블기반 평가척도에서 유사한 것으로부터, EPS에 비해 ECC가 실제 레이블보다 더 많은 레이블을 예측함을 알 수 있다.
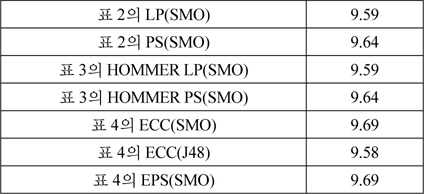
[표 5.] 유전자 온톨로지 가중을 사용한 다중레이블 분류기 성능
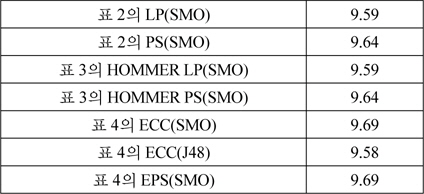
유전자 온톨로지 가중을 사용한 다중레이블 분류기 성능
[표 6.] 다양한 평가 척도를 사용한 다중레이블 분류기의 성능
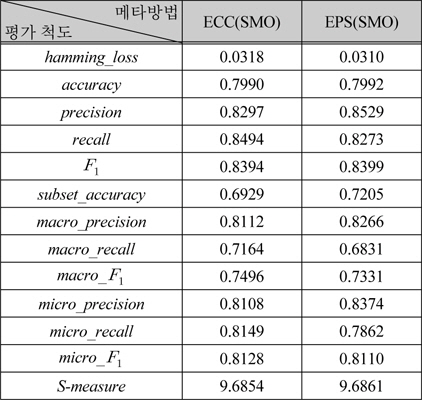
다양한 평가 척도를 사용한 다중레이블 분류기의 성능
표 6의 결과를 실험 방법은 약간씩 다르지만, 동일한 단백질 자료를 사용하는 다른 방법들과 비교한다. 논문 [3]의 실험결과에 따르면, 최근접-이웃 분류기를 배깅으로 조합하는 Hum-mPLOC 2.9[1]은
본 연구에서는 기본 설정의 파라미터를 가진 다중레이블 분류방법을 사용하였음에도 불구하고, 비교한 논문들의 방법보다 성능이 높았다. 따라서 우수한 접근법인 EPS, ECC를 문제에 적합하게 최적화하면 더욱 향상된 성능을 얻을 수 있다고 판단된다.
본 논문에서는 단백질의 세포내 위치 예측을 위하여 여러 다중레이블 분류방법을 광범위하게 비교하였다. 또한, 다중레이블 분류방법을 비교하기 위하여 일부분 척도가 보다 다양한 척도를 사용하여 다양한 관점에서 요약할 수 있는 척도로 쉽게 비교하여 적합한 방법 선택할 수 있게 하였다.
비교 실험을 통하여 살펴보면, 단백질을 세포내 위치 예측에는 세포내 위치간의 연관관계를 학습 모델에 포함하는 방법이 성능이 높았다. 이러한 연관관계를 자료의 속성에 추가하는 CC(classifier chain)나 관련된 레이블 부분 집합으로 직접적으로 레이블간의 연관관계를 표현하고 적은 빈도의 집합을 제거하는 PS(Pruned sets)를 사용하여 여러 분류기를 구성하고 이를 배깅으로 조합하는 것이 가장 성능이 좋았다.
본 논문에서는 많은 수의 분류기를 비교하기 위하여 기본적인 설정을 사용하였으나, 향후에는 효과적인 것으로 밝혀진 CC나 PS로 구성된 여러 분류기를 조합하는 방법을 최적화하고, 분류기를 구성할 때 사용되는 단일 분류기의 파라미터를 최적화하는 것이 필요하다.