최단강하선 문제의 해는 cycloid 형태라는 것이 밝혀졌으나, bead의 정확한 각도 값은 복잡한 비선형방정식의 역관계를 테이블 형태로 구해야 얻을 수 있다. 본 논문에서는 이러한 근사해의 정확도를 높이기 위해 신경회로망을 이용하여 비선형방정식의 역관계식을 표현하였고, 신경회로망의 보간 기능으로 인해 높은 정확도의 최단시간제어가 가능하였다. 여러 가지 최종목표점에 대한 컴퓨터 시뮬레이션을 통해서 본 논문에서 제안한 방법이 기존의 방법보다 우수함을 확인할 수 있었다.
The solution of brachistochrone problem turned out the form of a cycloid but correct angle values of bead can be obtained from the table form of inverse relations for the complicated nonlinear equations. To enhance the accuracy, this paper employs the neural network to represent the inverse relation of the complicated nonlinear equations. The accurate minimum-time control is possible with the interpolation property of the neural network. For various final target points, we have found that the proposed method is superior to the conventional ones through the computer simulations.
최단강하선(Brachistochrone) 문제의 해법은 중력장 내의 인공위성 또는 항공기가 최소시간으로 이동하기 위한 제어방법이나 무인 로켓의 최소 시간 궤적 설계 등에 응용될 수 있다. Johann Bernoulli에 의해서 제기된 최단강하선 문제는 최소시간제어 문제로 질량이
본 논문에서 이러한 근사오차를 감소시키기 위해 일반화와 보간 기능을 갖는 신경회로망을 사용하여 최적 제어 각도의 정확도를 높여 bead가 최단시간으로 주어진 최종점에 도달하도록 하고자 한다. 또한 신경회로망은 입력층(input layer), 히든층(hidden layer), 출력층(output layer)의 뉴우런 개수에 따라 신경회로망의 복잡도, 학습에 걸리는 시간, 학습의 성능 등에 매우 큰 영향을 미친다[4-6]. 신경회로망의 빠른 학습과 수렴 정도를 올리기 위하여 신경회로망의 입출력 변수를 단일 입출력 변수가 되도록 관련 수식이 유도될 수 있다. 단일 입출력 변수로 구성된 신경회로망 최적제어기법은 입출력 개수가 줄고 입출력 함수 관계가 단순하여 적은 뉴우런의 개수로도 학습 시간과 학습 오차가 매우 줄어 듦을 알 수 있으며, 실시간 제어에도 매우 적합하다. 본 논문에서 제안한 신경회로망을 이용한 최적제어기의 성능을 확인하기 위해서, 여러 가지 경우의 최종 bead 위치에 대해서 제어 성능을 모의 실험하였으며, 그 결과 본 논문에서 제안한 방법이 일반적인 최적화 방법보다 우수함을 확인할 수 있었다.
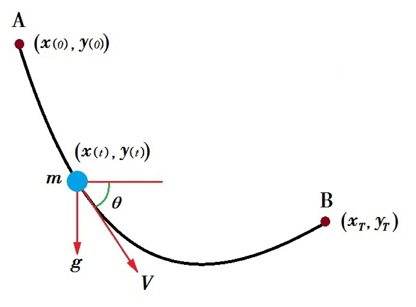
최단강하선 문제는 질량이 m인 bead가 수직 평면 위에 주어진 두 점 A, B에 대해 A점을 출발하여 중력 하에서 B점에 도착할 때 가장 짧은 시간이 걸리는 경로를 찾는 문제로, bead가 중력장에서 최단시간으로 운동하는 최적 경로를 찾는 문제이다.
그림 1과 같이 질량 m인 bead가 정지 상태에서 원점(
단,
위에서 초기 속도
그림 1에서 bead 운동을 미분방정식으로 표현하면
최단시간문제이므로 성능지수(performance index)는 아래와 같이 정의하였다.
단,
위에서 각도 𝜃 는 최단시간 경로를 찾기 위한 제어 변수로, Frank L. Lewis[3]가 제시한 최종상태가 고정된 함수를 갖는 비선형 최적제어기 설계를 사용하여, 최단 강하선 문제에 대입하면 최적 제어량 𝜃(
최종 시간
식(6), (7)은 다음과 같이 식(8), (9)와 같이 간단하게 표현될 수 있다[3]. 식(9)는 초기조건[𝜃(0) = 90° ⇒ 𝜙(0) = 0° ,
단, 이다.
식 (8)을 초기 조건을 만족하도록 다시 정리하면 아래 식(10)과 같이 표현된다.
방정식의 좌측 항을 상수항으로 식을 정리하면 식 (11)과 같다.
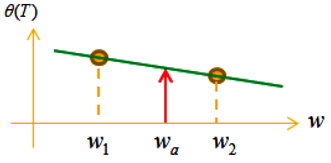
앞에서의 식(8), (9)는 cycloid 곡선을 의미하며, 이는 위에서 수식이 최소시간 경로임을 확인할 수 있다. 식(11)로부터 𝜃(
𝜃(
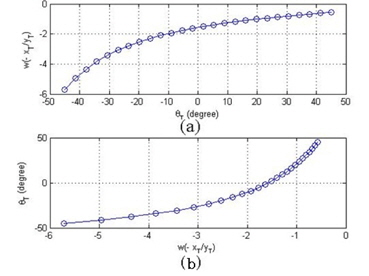
인공신경회로망은 생물체의 뇌 신경세포들의 연결관계를 단순화시켜 이를 수학적으로 표현하여 인간의 두뇌가 가지는 기능을 구현하고자 하는 시스템이다. 본 논문에서는 가장 일반적으로 사용되는 앞먹임 신경회로망(feedforward neural networks) 구조를 취하고, 역전파 학습 알고리즘(back propagation learning algorithm)을 사용하여 신경회로망을 학습하였다[4-6]. 신경회로망의 보간 기능을 위하여 위의 식(11)을 사용하여 입출력 데이터의 역관계를 표현하였다. 이렇게 구성된 신경회로망은 임의의 목표점(
적절히 세분화된 𝜃(
신경회로망의 학습을 위해 𝜃(
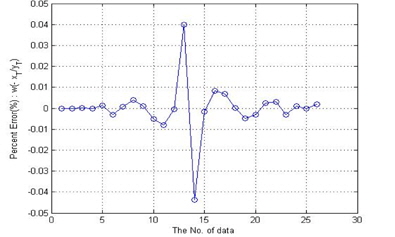
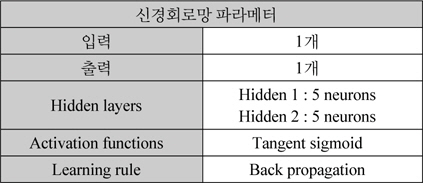
그림 4는 표 1과 같이 신경회로망의 학습을 위한 파라메터들을 설정하여 학습한 후, 학습 데이터에 대한 퍼센트 오차를 표시하였다. 신경망 학습 데이터는 비선형이 크지 않고 부드러운 곡선 모양을 갖고 있어 신경회로망의 학습이 매우 용의하고, 신경회로망의 히든층 뉴우런 개수가 적어도 학습이 매우 잘 됨을 알 수 있다.
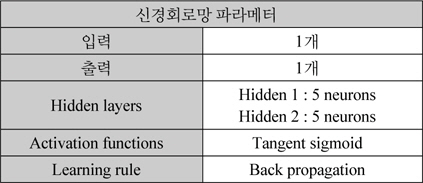
신경회로망 파라메터
신경회로망을 이용한 시간 최적제어의 성능평가를 위해서 다음과 같이 2가지로 근사된 최적제어방법들을 사용하였다[7,8]. 임의의 최종점 (
모의실험을 위하여 중력 가속도
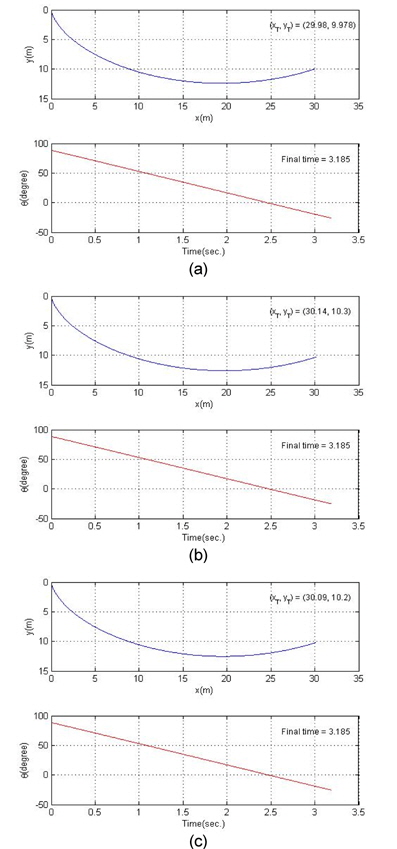
그림 6은 여러 가지 최종점에 대한 모의 실험 경우 중, 최종점의 위치가 (
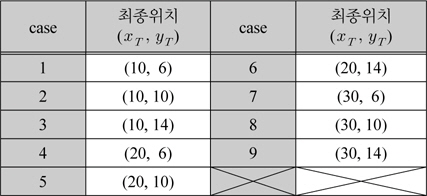
표 2는 제안된 제어기와 일반적인 최적 제어기들의 성능 평가를 위하여 다양한 최종점을 표시하였다.
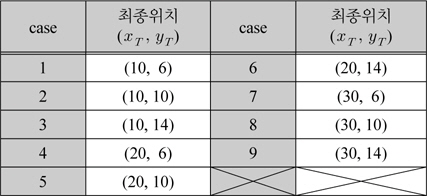
제어기 성능 비교를 위한 다양한 최종점
다양한 최종점에 대해 3가지 제어기법 모두 수렴 시간에 있어서 비슷한 수렴시간을 얻었다. 이것은 비선형다 변수 입력을 갖는 수식의 해 𝜃(
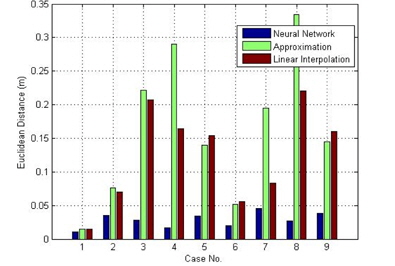
수렴 정도에 있어서는 모든 최종점에 대하여 신경회로망에 의한 최적제어기법이 다른 최적제어기법들에 비하여 뛰어난 성능을 보임을 알 수 있다. 그림 7은 표 2의 9가지 최종점에 대하여 신경회로망 최적 제어기법과 일반적인 최적 제어기법들의 수렴 정도를 막대 그래프로 나타내었다. 신경회로망을 사용한 최적 제어기법은 모든 최종점에 대하여 수렴정도가 0.05(Euclidean distance) 안에 존재함을 알 수 있다. 이는 다른 최적 제어기법에 비하여 매우 뛰어난 성능을 나타내었다.
최단강하선 문제의 해는 cycloid 형태라는 것이 밝혀 졌으나 bead의 정확한 각도 값은 비선형방정식을 풀어야 얻을 수 있다. 따라서 최단강하선 문제를 최적제어 문제로 해석하여 bead의 최적제어 각도를 그래프 또는 테이블 형태의 근사치로 구할 수 있으나, 이러한 테이블 형태로 주어지는 최적제어 각도는 테이블을 얼마나 세분화하는가에 따라 다르다. 따라서 최적제어 각도를 무한히 세분화할 수 없으므로 근사오차가 발생한다.
본 연구에서는 이러한 근사오차를 감소시키기 위해 일반화 및 보간 기능을 갖는 신경회로망을 선택하여 bead가 갖는 최적제어 각도의 정확도를 높여 최단시간에 최종점에 도달하도록 하였다. 여러 가지 경우의 최종점에 대해 모의 실험한 결과 본 논문에서 제안한 방법이 일반적인 최적제어 방법보다 매우 우수함을 확인할 수 있었다.