최근 CMOSFET를 이용한 마이크로프로세서 및 메모리반도체는 고속/저전력용으로 발전하기 위하여 초소형 트랜지스터을 요구하게 되었다. 그러나 기존의 CMOSFET구조는 10nm이하의 채널 길이로 제작하기 위해선 심각한 단채널 효과 문제가 발생하여 트랜지스터로서 제대로 작동할 수 없게 된다. 채널길이의 감소는 전류량의 증가, 입력커패시턴스의 감소, 스위칭주파수의 증가 및 셀 면적의 감소 등과 같은 중요한 출력효과를 나타내는 반면, 문턱전압의 이동, 드레인 유도 장벽감소, 문턱전압이하 스윙특성 저하 및 항복전압특성저하 등과 같은 심각한 단채널 효과에 의한 소자기능저하를 발생시키고 있다. 이러한 문제점 중 문턱전압이하 특성의 저하는 트랜지스터의 온-오프 동작에 문제점을 야기시켜 디지털회로에 오동작을 일으키게 된다. 트랜지스터 구조를 개선하여 단채널 효과를 해결하기 위한 연구 결과, CMOSFET를 대치할 가장 각광받는 차세대 트랜지스터 소자로서 다중게이트 (Multi Gate) MOSFET를 개발하게 되었다[1-3]. 다중게이트 소자는 여러 가지 형태로 개발되고 있으며 그중 가장 간단하며 제작이 용이한 소자가 상하에 게이트단자를 제작하여 채널 내 전하의 제어능력을 향상시킨 이중게이트 MOSFET소자이다. 기존의 CMOSFET와는 달리 이중게이트 MOSFET는 게이트를 두 개 제작하여 게이트의 전류제어능력을 향상시키고 이로 인하여 채널길이 감소에 의한 단채널 효과를 줄여줄 수 있다고 알려져 있다. 본 연구에서는 이러한 이중게이트 MOSFET가 채널크기 변화에 따라 발생하는 문턱전압이하 전류의 변화를 분석하였다. 문턱전압 전류모델은 Tiwari의 포아송 방정식에 대한 해석학적 전위모델을 이용하였다[4]. Tiwari의 전위모델에 대한 타당성은 여러 논문에서 이미 언급한 바와 같이 수치해석학적 해와 매우 잘 일치하므로 본 연구에서는 가우스함수를 전하분포함수로 이용한 Tiwari의 전위모델을 사용하였다[5-6]. Tiwari등은 전위모델을 이용하여 문턱전압 등을 분석하였으나 문턱전압이하 전류특성에 대해선 언급하지 않았으므로 본 연구에서는 채널크기 변화에 따라 발생하는 단채널효과 중 문턱전압이하 전류변화에 대하여 분석하였다. 또한 이중게이트 MOSFET는 두 개의 게이트 단자를 가지므로 상하단의 게이트 단자에 의한 영향을 분석하기 위하여 상단부분과 하단부분으로 흐르는 전류의 채널길이 및 채널두께에 대한 변화도 함께 분석하였다.

2장에서는 포아송방정식의 해석학적 전위모델 및 전류모델에 대하여 설명하였으며 3장에서 이 모델을 적용하였을 경우, 문턱전압이하 전류의 채널크기에 대한 변화를 고찰하였다. 또한 4장에서 결론을 맺었다.

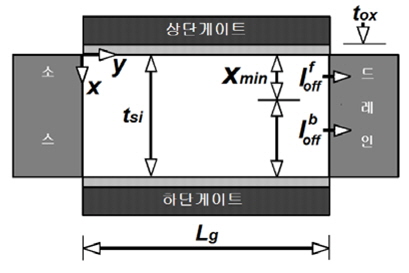
그림 1은 이 논문에서 사용한 이중게이트 MOSFET의 이차원 개략도이다. 상단게이트와 하단게이트는 상호 대칭적인 구조를 하고 있으며 구조의 z방향에 대한 전위분포는 거의 일정하므로 단지 x와 y방향에 대한 전위분포를 구하기 위하여 Tiwari 등의 계산방법과 동일하게 포아송방정식을 풀어 전위분포 ϕ(x,y)를 구한다[4].

차단전류를 구하기 위하여 상하단 게이트전압의 영향에 의하여 전위분포가 x방향으로 최소인 점을 x_min이라 할 때, 두 부분으로 전류를 나누어 합산한다. 즉,

이다.

Havaldar 등[7]은 3차원으로 전개하였으나 전술한바와 같이 z방향으로의 대칭성 때문에 본 연구에서는 2차원으로 전개방식을 이용하면 상단전류와 하단전류는 다음과 같이 유도할 수 있다.

여기서 W는 채널폭, V_t는 열전압, μ_n은 전자이동도, n_i는 순수반도체의 전자농도, V_DS는 드레인전압, ϕ_min (x)는 표면전위 ϕ_s가 최소가 되는 y점에서의 x방향 전위분포이다. 또한 N_p는 포아송방정식을 풀 때 사용하는 도핑분포함수 n(x)에 나타나는 이온주입 시 도즈량에 의하여 결정되는 최대 도핑분포 값이다. 즉, 포아송방정식을 풀 때 다음과 같은 가우스 함수를 이용하였다.

여기서 R_p와 σp는 각각 이온주입범위 및 분포편차를 나타낸다. n(x)는 채널 내 두께방향 즉, 깊이방향으로의 불순물원자 분포함수로서 y와 z방향으로는 일정하게 분포되며 단지 x방향으로만 변화한다고 가정하였다. 식(2)와 식 (3)을 풀면 다음과 같은 해석학적 차단전류 모델을 구할 수 있다.

여기서 는 상단 게이트단자와 접하는 표면전위중 y = y_min일 때의 전위이며 는 하단 게이트단자와 접하는 표면전위 중 y = y_min때의 전위이다. 이론적으로 x방향으로 대칭적인 전위를 보인다면 x_min =t_si/2 지만 이온주입범위 R_p와 분포편차 σ_p에 따라 x_minmin값은 변화를 겪게 된다. 그러므로 상단전류 와 하단전류 는 총 차단전류에서 차지하는 비율이 변화하게 된다. 본 연구에서는 이와 같이 이온주입범위 및 분포편차에 따라 변화하는 상하단 차단전류와 각각에 대한 총 차단전류에 대한 비를 고찰하였다.

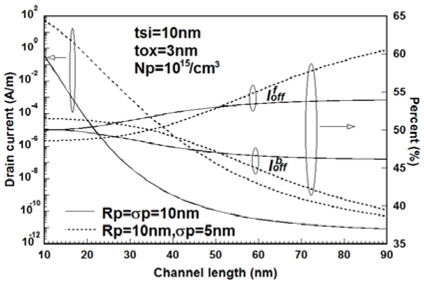
식 (5)와 식(6)의 문턱전압이하 전류모델의 타당성은 기존에 발표된 논문[6]에서 이미 언급하였으므로 이 절에서는 채널크기 변화에 대하여 고찰하였다. 그림 2에 채널길이 변화에 대한 문턱전압이하 전류의 변화를 도시하였다. 상단전류 와 하단전류 변화를 채널길이 변화 및 가우스함수의 파라미터인 이온주입범위 그리고 분포편차의 변화에 대하여 도시하였다. 단채널 효과에 의하여 채널길이가 감소할수록 문턱전압이하 전류는 크게 증가하는 것을 알 수 있다. 또한 채널길이가 증가하면, 대칭적인 구조이지만 가우스함수분포에 의한 전하분포에 따라 상단전류가 하단전류보다 문턱전압이하 전류에 대한 구성비가 증가하는 것을 알 수있다. 그러나 이는 이온주입범위 및 분포편차의 변화에 따라 크게 변화하였다. 즉, R_p = σ_p = 10 nm인 경우는 채널길이가 약 10 nm정도에서 상단전류의 구성비와 하단전류 구성비가 거의 동일하며 약 45 nm정도 이상의 채널길이에선 구성비가 거의 일정하게 유지되고 있다는 것을 관찰할 수 있다. 그러나 이온주입범위는 일정하게 유지하면서 단지 분포편차를 감소시켜 전하분포의 모양을 변화시키면 즉, σ_p = 5 nm로 감소시키면 채 널길이가 약 35 nm이하에선 오히려 하단전류의 구성비가 상단전류의 구성비보다 크게 유지되다가 35 nm이상의 채널길이에서 상단전류의 구성비가 급격히 증가하는 것을 관찰할 수 있다. 이와 같이 상하단 전류의 구성비는 전하분포함수인 가우스함수의 모양에 따라 크게 변화하였다. 문턱전압이하 전류도 가우스함수의 모양에 영향을 받아 σ_p = 5 nm로 분포편차가 감소하면 증가추세를 보이고 있었다. 그러나 채널길이가 증가하면 증가분이 감소하여 가우스함수의 모양에 영향을 덜 받는 것을 알 수 있었다.

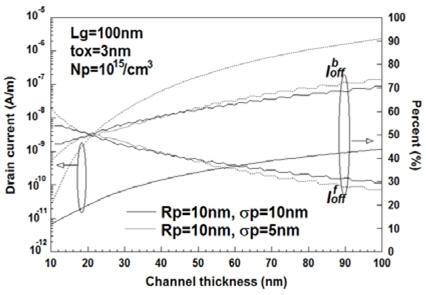
채널두께의 변화에 대한 문턱전압이하 전류의 변화를 고찰하기 위하여 그림 3에 채널길이가 100 nm일 때 의 결과를 도시하였다. 그림 2의 결과와는 달리 채널두께가 증가할수록 하단전류의 구성비가 증가하고 있었다. 그러나 채널 두께가 약 20 nm이하에선 상단전류의 구성비가 더욱 크게 분포하였다. 가우스함수의 모양을 결정하는 이온주입범위 및 분포편차의 변화에 대하여 고찰해 보면 상하단전류의 구성비의 경우, 가우스함수의 모양에 따른 변화는 거의 나타나지 않았다. 그러나 분포편차가 10 nm에서 5 nm로 감소할 경우, 문턱전압이하 전류는 채널두께가 증가할수록 크게 증가하고 있다는 것을 알 수 있었으며 이 때 문턱전압이하 전류의 차는 채널두께가 감소할수록 일정하게 유지되다가 채널두께가 상하단전류의 구성비가 역전되는 20 nm이하로 감소하면 차가 급격히 감소하는 것을 관찰할 수 있었다.

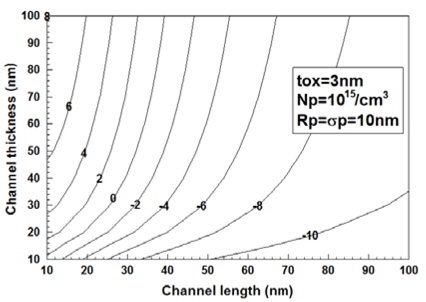
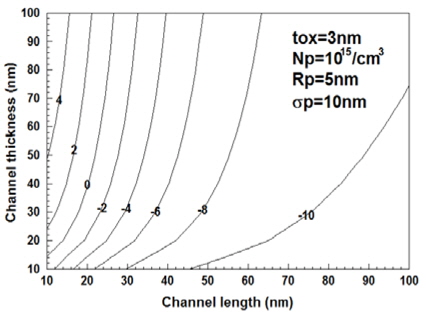
채널두께 및 채널길이에 대한 문턱전압이하 전류의 변화를 고찰하기 위하여 그림 4에 문턱전압이하 전류의 승수변화에 대한 등고선 그래프를 도시하였다. 채널길이가 짧아지면 단채널효과에 의하여 문턱전압이하 전류가 급격히 상승하고 있다는 것을 관찰할 수 있다. 일반적으로 채널두께보단 채널길이를 길게 제작하므로 채널길이가 채널두께보다 길 경우, 상대적으로 문턱전압이하 전류가 감소하는 것을 알 수 있다. 특히 채널길이가 채널두께보다 매우 길어지면 문턱전압이하 전류는 매우 작아지나 상대적으로 이중게이트 MOSFET의 크기가 커지는 문제가 있다. 그러므로 채널길이와 채널두께의 결정은 문턱전압이하 전류의 관점에서 볼 때 매우 민감한 사항이다.

가우스함수의 변수인 이온주입 범위 및 분포편차의 변화에 대한 문턱전압이하 전류의 변화를 관찰하기 위하여 그림 5와 그림 6에 이온주입 범위 및 분포편차를 5 nm로 변화시킨 문턱전압이하 전류의 변화를 도시하였다. 이온주입범위를 변화시킨 그림 5와 그림 4를 비교해 보면 동일한 채널길이와 채널두께를 가진 경우, 이온주입 범위가 감소하면 문턱전압이하 전류의 크기가 상대적으로 감소하고 있다는 것을 알 수 있다.

그러나 감소 정도는 매우 미미하여 이온주입 범위의 변화에 대한 문턱전압이하 전류의 변화는 거의 무시할수 있을 정도라는 것을 알 수 있다. 그림 4와 동일하게 채널두께가 작을 경우 채널길이에 따른 문턱전압이하 전류의 변화가 더욱 크게 나타나며 채널두께가 클 경우, 상대적으로 채널길이 증가에 따른 문턱전압이하 전류의 변화가 완만하게 나타나고 있다는 것을 관찰할 수 있다. 그러나 변화정도는 채널길이가 길 경우, 이온주입 범위가 작은 그림 5의 경우가 더욱 완만하게 나타나고 있다.

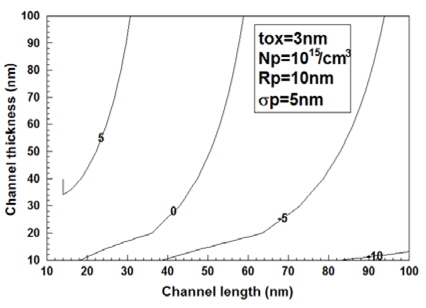
문턱전압이하 전류의 분포편차에 대한 변화를 고찰하기 위하여 그림 6에 분포편차를 5 nm로 감소한 경우, 문턱전압이하 전류의 변화를 도시하였다. 그림 2와 그림 3에서 관찰한 바와 같이 분포편차가 감소하면 문턱전압이하 전류가 크게 증가하고 있다는 것을 알 수 있었다. 특히 채널길이가 길고 채널두께가 두꺼울 경우, 문턱전압이하 전류의 증가가 더욱 심각하게 나타나고 있다는 것을 알 수 있다. 분포편차가 5 nm로 감소한 경 우, 그림 4와 비교해 보면 10^-10A/m 이하의 우수한 문턱전압이하 전류를 나타내기 위해서 채널길이는 80 nm이상 이어야하며 채널두께는 15 nm이하이어야만 한다는 것을 알 수 있다. 이와 같이 분포편차가 작아지면 채널두께가 현저히 작아져야만 문턱전압이하 전류특성이 우수하다는 것을 알 수 있다.

본 연구에서는 이중게이트 MOSFET의 채널크기 변화 및 전하분포의 변화에 따른 문턱전압이하 전류의 변화를 분석하였다. 나노소자인 이중게이트 MOSFET에 대한 정확한 해석학적 분석을 위하여 전위분포는 포아송방정식을 이용하여 구하였으며 이때 전하분포함수에 대하여 가우시안 함수를 사용하였다. 가우시안 함수의 변수인 이온주입범위 및 분포편차 그리고 채널크기 등에 대하여 문턱전압이하 전류 특성의 변화를 관찰하였다.

결과적으로 문턱전압이하 전류는 채널길이 및 채널두께의 변화에 크게 영향을 받으며 채널길이가 증가할수록 그리고 채널두께가 감소할수록 감소하는 것을 알수 있었다. 전하분포의 변화에 대한 문턱전압이하 전류의 변화를 고찰해본 결과 분포편차가 감소할수록 문턱전압이하 전류는 증가하는 것을 알 수 있었다. 그러므로 분포편차가 5 nm정도로 감소하였을 경우 시뮬레이션 조건에서 문턱전압이하 전류가 10^-10A/m 이하정도로 우수한 값을 갖기 위해선 채널두께는 15 nm이하로 매우 작아져야하는 문제점을 나타냈다. 상대적으로 이온주입 범위의 변화는 문턱전압이하 전류값에 그리 큰 영향을 미치지 않는 것을 알 수 있었다. 상·하단전류의 구성비 또한 채널크기 및 이온주입 범위 그리고 분포편차에 따라 크게 변화하였다. 이와 같이 문턱전압이하전류는 채널의 크기변화 및 전하분포함수의 모양에 따라 크게 변화하므로 이중게이트 MOSFET 설계 시 주의하여야 할 것이다.