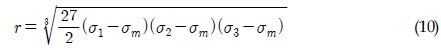This paper discusses a new formulation for the failure strain in the average stress triaxiaility domain for a low-temperature high-strength steel (EH36). The new formula available at a low average stress triaxiality zone is proposed based on the comparison of two results from tensile tests of flat type specimens and their numerical simulations. In order to confirm the validity of the failure strain formulation, a user-subroutine was developed using Abaqus/Explicit, which is known to be one of the most popular commercial finite element analysis codes. Numerical fracture simulations with the user-subroutine were conducted for all the tensile tests. A comparison of the engineering stress–strain curves and engineering failure strain obtained from the numerical simulation with the user-subroutine for the tensile tests revealed that the newly developed user-subroutine effectively predicts the initiation of failure.
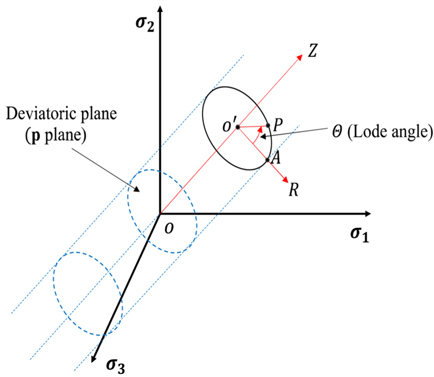
선박 또는 해양플랜트의 구조용 강재는 연성재료(Ductile material)로 간주되며, 이러한 연성재료로 만들어진 구조물이 외력을 받아 구조물 내부에서 발생한 응력장(Stress field)이 파단을 지배하는 것으로 알려져 있다. von Mises 항복조건은 연성재료에 가장 적합한 것으로 알려진 항복조건이기 때문에, 많은 연구자들은 파단도 von Mises 등가응력(von Mises equivalent stress) 또는 von Mises 등가소성변형률(von Mises equivalent plastic strain)이 지배할 것으로 예측해왔다. 그러나 최근의 연구 사례로부터 파단은 응력 삼축비(Stress triaxility)와 로드각(Lode angle)의 함수로 인식되고 있다. 응력 삼축비는 정수압응력 (Hydrostatic stress)과 편차응력(엄밀하게 von Mises 등가응력)의 비이므로, 높은 응력 삼축비는 정수압응력이 편차응력에 비하여 많이 발달하였다는 의미이다. von Mises 항복조건을 사용할 때 정수압 응력이 소성변형에 기여하지 않지만 파단에 영향을 미친다는 사실을 주지할 필요가 있다. 로드각은 항복면에 직교하는 편차응력평면(Deviatoric plane)을 이용하여 응력의 성분 또는 상태를 표현하기 위한 각도이다.
이러한 응력 삼축비와 로드각이 파단에 미치는 영향에 대하여 많은 연구가 진행되고 있다. Bao and Wierzbicki(2004)는 알루미늄 시편에 대한 압축, 전단, 인장, 인장-전단 실험을 실시하였으며, 평균 응력 삼축비의 개념을 최초로 도입하였다. Bai and Wierzbicki(2008)는 수정 Mohr-Coulomb (MMC, modified Mohr-Coulomb) 항복조건을 개발하고, 이에 상응하는 파단 변형률을 응력 삼축비와 로드각의 함수로 나타내었다. 이 파단 조건은 Bai and Wierzbicki(2010), Luo and Wierzbicki(2010), Dunand and Mohr(2011), Beese and Mohr(2011), Luo et al.(2012) 등에 의하여 타당성이 증명되고 있다.
조선해양 산업계에서는 주로 충돌, 좌초, 폭발과 같은 대변형 및 대변형률을 유발하는 문제에서 파단을 중요한 문제로 인식하고 있다. 사고로 인한 파공의 크기를 예측하기 위하여 파단조건의 설정이 가장 중요하기 때문이다. RTCL(Rice-Tracey and Cockcroft-Latham) 파단조건은 Urban(2003)과 Törnqvist(2003)에 의하여 제시되어 현재까지도 많은 연구에 응용되고 있다 (Nguyen et al., 2011; Haris and Amdahl, 2013; Liu et al., 2011). Choung(2009)과 Choung et al.(2010)은 기공률(Porosity)을 파단조건으로 사용하여 파단을 수치 해석적으로 구현한 바 있다. 가장 일반적인 파단조건은 파단 변형률로서 과거에는 파단 변형률이 상수로 인식되었지만, 최근에는 파단 변형률을 변수로 인식하고 이를 예측하기 위한 연구가 진행되고 있다. Choung et al.(2011; 2012)는 EH36 강재의 환봉형 노치재에 대한 실험과 수치해석을 통하여 파단 변형률을 평균 응력 삼축비의 함수로 정식화하였고, Choung and Nam(2013)은 동일 강재의 판상형 노치재에 대한 실험을 추가적으로 실시하여 낮은 평균 응력 삼축비 영역에서 파단 변형률의 변화를 관찰하였다.
본 논문은 기존의 연구(Choung et al., 2011; Choung et al., 2012; Choung and Nam, 2013)결과를 보충하기 위하여 추가적인 실험을 실시하여 낮은 평균 응력 삼축비에 대한 정식화를 실시하였다. 또한 정식화된 파단 변형률의 검증하기 위하여 정식화된 파단 변형률을 상용유한요소코드인 Abaqus.Explicit (Simulia, 2008)의 사용자-서브루틴 (User-subroutine)에 이식하여 그 유효성을 검증하였다.
본 논문이 참조한 참고문헌(Choung et al., 2011; Choung et al., 2012; Choung and Nam, 2013)에는 국내 P사에서 제조한 저온용 고장력강 EH36을 대상으로 각종 노치재에 대한 인장실험을 실시한 결과가 수록되어 있다. 이를 요약하자면 다음과 같다.
시편의 기본 형상은 환봉형(Round bar type)과 판상형(flat bar type)의 2가지이며, 다양한 노치의 크기를 포함하여 설계 및 가공되었다. 평활재(Smooth specimen)의 경우 Fig. 1 (a)에 보인바와 같이 ASTM(2004)에서 제시하는 시편 설계기준을 적용하였으며, 노치의 크기에 따른 파단특성의 변화를 관찰하기 위하여 Fig. 1(b), (c)에 보인바와 같이 다양한 크기를 가지는 노치재가 환봉형과 판상형으로 제작되었다. 환봉형 및 판상형의 노치 종류는 평활재 포함하여 12가지 및 10가지였다. 강재의 가공방향(Rolling direction)을 고려하여 가공 평행방향(Longitudinal direction) 시편과 가공 직교방향(Transverse direction) 시편으로 나누어 시편을 가공하였다. 모재의 두께가 25mm였기 때문에 두께 방향 위치에 따라 상층(Top layer), 중층(Middle layer), 하층(Bottom layer)에 대하여 2mm두께의 판상형 시편이 가공되었다. 반면 환봉형은 두께에 따른 층의 분류가 불가능하였으며, 대체적으로 층별 평균적인 특성치를 나타낸다고 볼 수 있다.
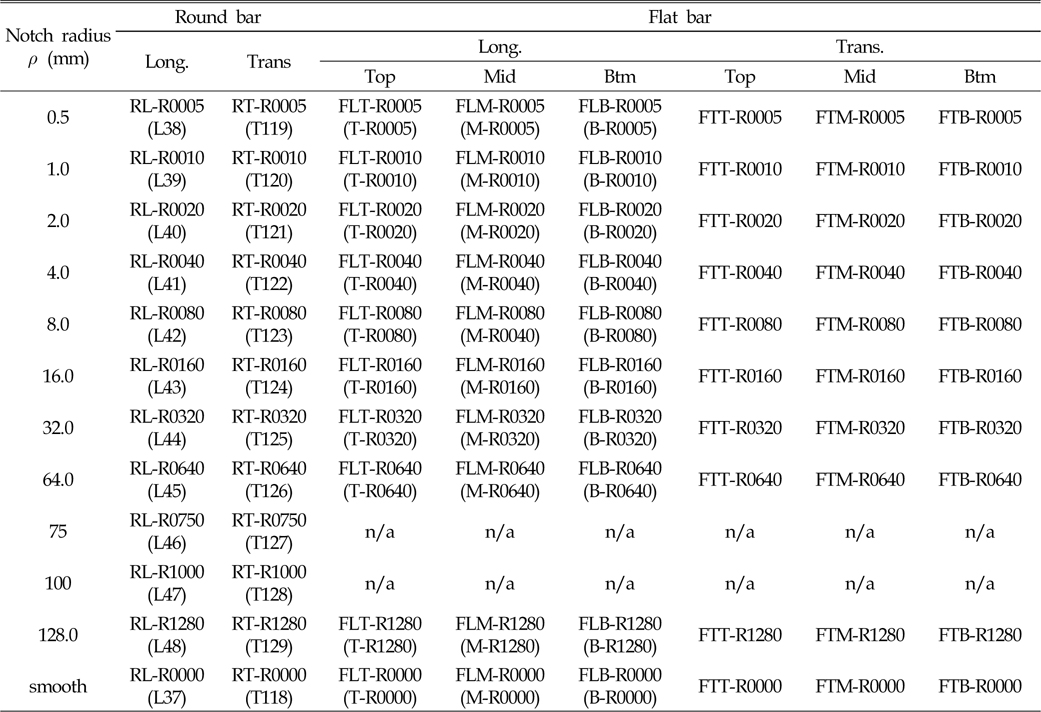
본 논문에서는 환봉형 및 판상형 시편의 이름을 각각 노치크기, 가공방향, 두께 층에 따라 Table 1과 같이 다시 명명하였으며, 여기서 괄호안의 표기는 참고문헌(Choung et al., 2011; Choung et al., 2012; Choung and Nam, 2013)에서 사용했던 시편의 이름을 나타낸다. 단 Table 1의 가공 직교방향으로 제작된 판상형 시편의 경우에는 본 논문을 통하여 제작되고 새로이 실시된 실험임을 밝힌다.
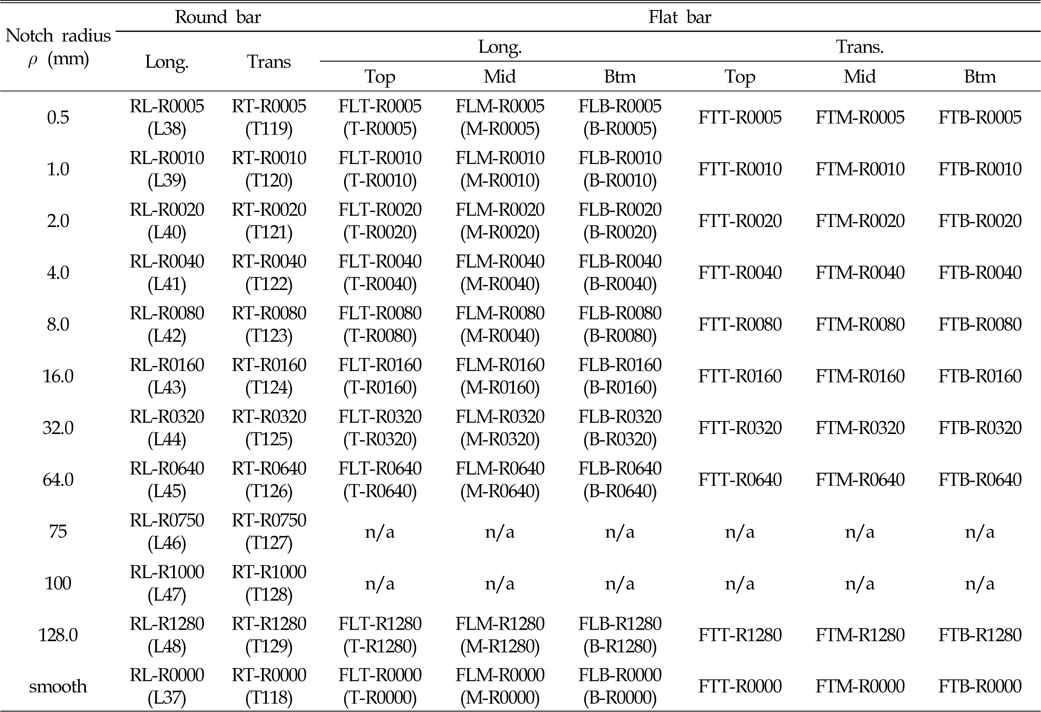
Labels of specimens
비선형 유한요소해석을 위해서는 초기 항복응력 뿐만 아니라 대변형률 구간까지의 유동응력을 도출해야 한다. 참고문헌(Choung et al., 2011; Choung et al.,2012)에서는 대변형률 구간에서의 유동응력을 도출하기 위하여 식 (1), (2)를 이용하여 공칭응력 – 공칭변형률 곡선을 얻은 후, 식 (3), (4)를 이용해 균일 진응력 – 균일 진변형률 곡선을 얻었다, 또한 네킹 이후의 진응력을 얻기 위하여 균일 진응력 - 균일 진변형률 곡선을 식 (5)에 곡선 적합 (Curve fitting)하여 재료상수
P : 인장 하중 A0 : 초기 단면적 l0 : 시편의 표점거리 δl : 표점거리 연신 S : 공칭 응력 e : 공칭 변형률 σun : 균일 진응력 εun : 균일 진변형률 σ : 진응력 εp : 소성 진변형률 K : 강도 계수 n : 소성 변형률 경화 지수
네킹 이후 대변형률 구간에서 소성 변형률이 증가하면서 평균 진응력(Average true stress)이 비선형적으로 증가하는 현상을 보정하기 위하여 실험에서 얻은 공칭응력 - 공칭변형률 선도를 수치해석에서 얻은 결과와 비교하면서 수정된 유동응력 곡선을 도출하는 방법을 적용한 바 있다(Choung and Nam, 2013). 이후 이 진응력을 수정 유동응력으로 정의한다.
재료나 구조물에 수십 퍼센트 이상의 큰 소성변형률이 발달하면 외삽 진응력의 부정확성으로 인하여 구조물의 소성 및 파단의 예측에 부정확도가 커지게 된다. 특히 평활재나 노치 반지름이 큰 시편과 같이 큰 소성변형률에서 파단이 예상되는 경우에는 반드시 수정 유동응력을 적용할 필요가 있다.
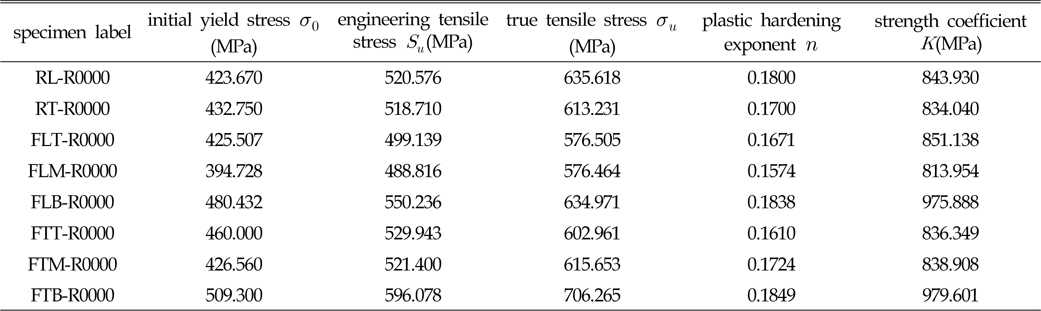
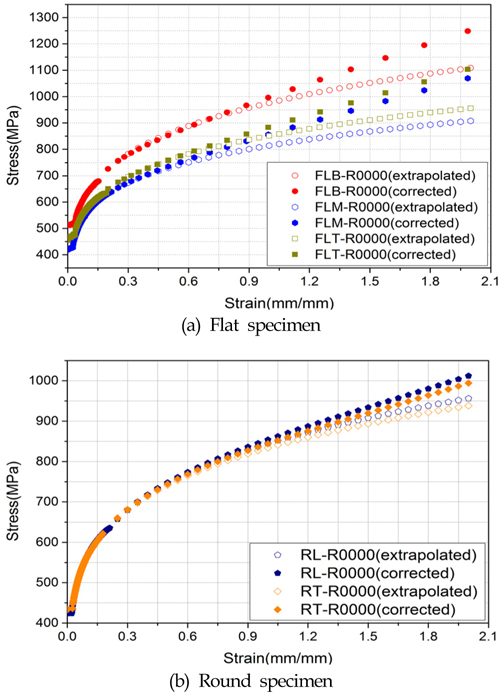
Fig. 2 (a)는 Choung et al.(2012)이 판상형 시편에 대하여 제시한 수정 진응력을 나타낸다. 환봉형 시편도 동일한 재료로 제작되었기 때문에 Fig. 2 (a)에서 도출한 수정 진응력의 기울기와 동일한 기울기를 가질 것으로 예측하여 Fig. 2 (b)에 나타내었다. 이후 수행될 모든 수치해석에서 Fig. 2의 수정 유동응력이 적용된다. 또한 초기 항복강도, 인장강도 등의 기계적 특성치를 Table 2에 요약하여 나타내었다.
[Table 2] Mechanical properties obtained from mechanical tests
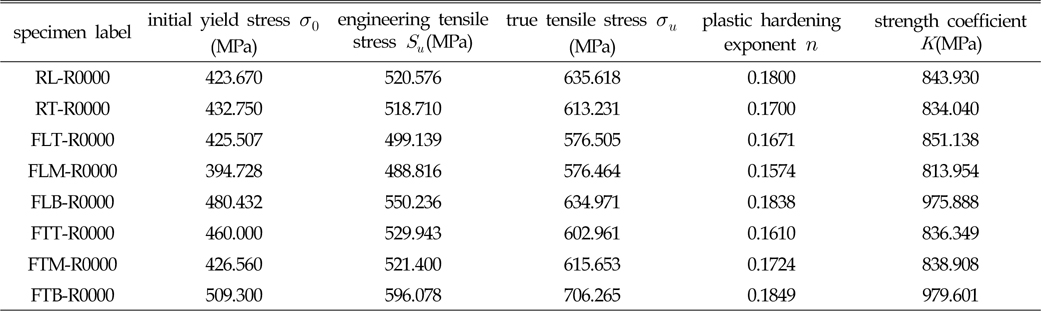
Mechanical properties obtained from mechanical tests
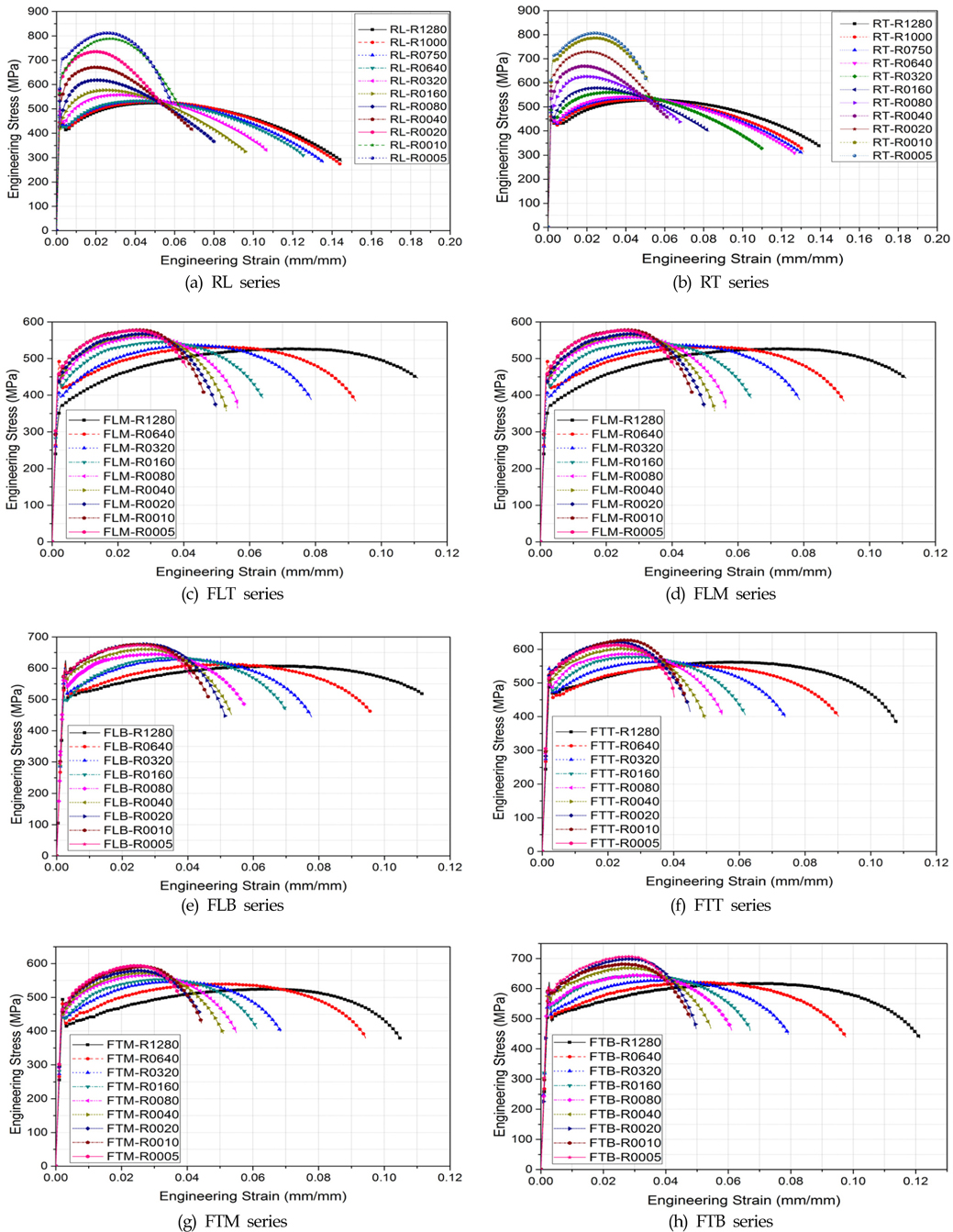
노치에 따른 인장하중과 연신률의 변화를 보기 위해 Fig. 3에 판상형 노치재 및 환봉형 노치재의 공칭응력-공칭변형률 곡선을 나타내었다. 모든 환봉형 시편의 단면적은 동일하고, 모든 판상형의 시편의 단면적도 동일하다. 그러나 노치 반지름이 커질수록 공칭 인장강도는 작아지고 파단까지의 연신률이 증가하는 것을 확인할 수 있다.
노치재 실험을 통하여 얻은 공칭응력-공칭변형률 곡선은 크게 다음의 용도로 사용된다. 첫 번째 노치재의 수치해석으로부터 얻은 공칭응력-공칭변형률 곡선과 실험 곡선을 비교하여 수치해석의 정량성을 검증하는데 사용된다. 두 번째 수치해석의 정량성이 검증된 후 실험과 수치해석을 비교하여 파단의 시점을 인지하는데 사용된다. 즉 파단 변형률 정식화를 위해서 파단이 발생하는 시점에서의 응력장(Stress field)과 변형률장(Strain field)이 요구되는데 실험으로부터 얻는 것이 불가능하므로 이를 수치해석으로부터 얻어야 한다.
세 개의 주응력 성분(
그러나 원통 좌표계를 정확하게 표현하기 위해서는 나머지 한 개의 좌표값
평균 응력 삼축비 (
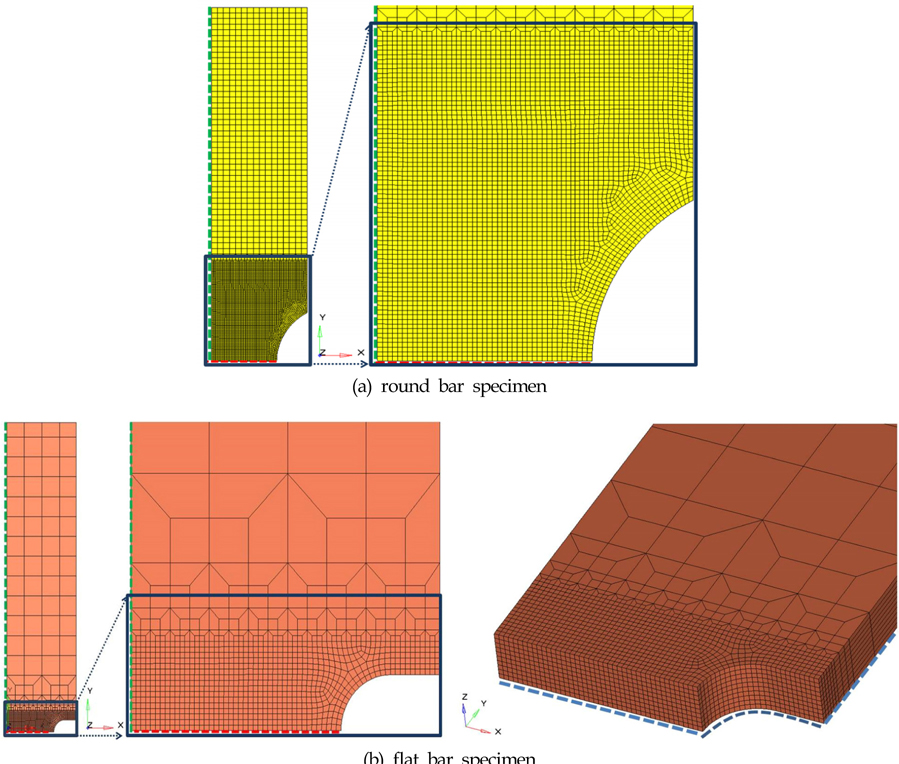
시편의 형상을 유한요소로 모델링하기 위하여 Altair/ HyperMesh(Altair, 2011)를 이용하였다. 수치해석에서 파단을 직접 구현하는 것이 아니라 파단의 개시 시점에서의 응력장과 변형률장을 수치해석으로부터 도출하는 것이 목표이므로 상용 유한요소해석 프로그램인 ABAQUS/Standard를 사용하였다. 환봉형 시편의 경우, 감차적분 4절점 축대칭 요소(CAX4R) 요소를 사용하여 해석시간의 효율을 극대화 하였다. 판상형 시편은 모든 축에 대하여 정확한 대칭 형상이므로 각 방향의 1/2만을 모델링(1/8 모델)하였다. 요소의 모델은 감차적분 8절점 고체요소(C3D8R)를 사용하였다.
환봉형 및 판상형 시편의 노치부에서
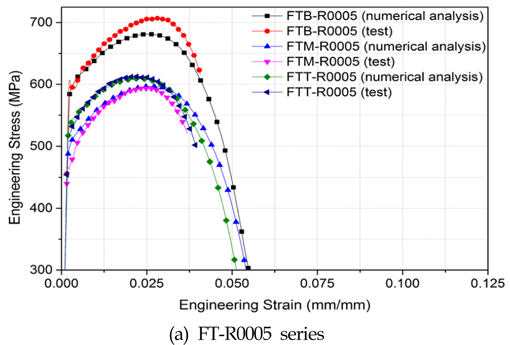
전술한 바와 같이 파단 변형률의 정식화에 선행하여 수치해석의 정확도에 대한 검증이 우선적으로 필요하다. 환봉형 시편의 경우 수치해석의 정량도는 이미 Choung et al.(2011; 2012)에 의하여, 가공 평행방향으로 제작된 판상형 시편의 경우 Choung and Nam(2013)에 의하여 검증된바 있다. 따라서 여기서는 가공 직교방향으로 제작된 판상형 시편의 수치해석 정량성만을 Fig. 6에 나타내었다. 시편의 노치가 커질수록 실험과 수치해석의 차이가 커지는 경향이 있지만, 전반적으로 실험과 수치해석이 일치하는 경향을 보이는 것으로 판단할 수 있다.
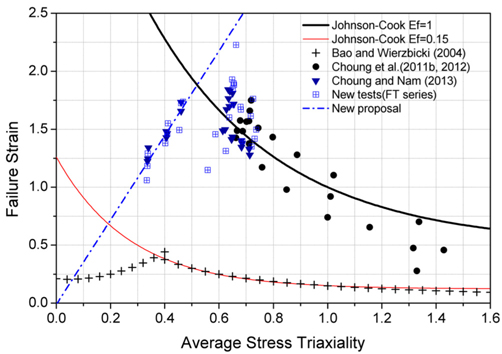
Choung et al.(2011 2012) 및 Choung and Nam(2013)은 무차원 임계에너지 수준에 따른 파단 변형률을 Johnson-Cook 파단 변형률 공식을 이용하여 정식화한바 있으며 이를 Fig. 7에 도시하였다. 무차원 임계에너지 수준에 따른 파단 변형률의 정식화는 예를 들어 100%, 80%, 60%, 등과 같이 일정한 간격을 두고 무차원 임계에너지 수준에 따른 파단 변형률 곡선을 만들어내는 것을 의미한다. 이와 같은 방법의 장점은 금속재료의 종류에 따라 무차원 임계에너지 수준만 달라지기 때문에 한번 정식화를 수행한 후 여러 금속재료에 대하여 응용이 가능하다는 것이다. Bao and Wierzbicki(2004)는 알루미늄 합금의 파단 변형률 곡선을 정식화한바 있는데, Choung et al.(2011; 2012)은 알루미늄 합금의 무차원 임계에너지가 EH36 강재의 15% 무차원 임계에너지 수준과 동일하다는 사실을 증명한바 있다. 정식화된 파단 변형률 곡선에 실험 결과를 같이 도시(평균 응력 삼축비와 파단 변형률의 값을 도시)하였으며, 무차원 임계에너지 수준을 확인할 수 있다.
본 논문에서는 새로이 실시된 판상형 시편 실험 및 Choung and Nam(2013)의 실험 결과를 토대로 작은 응력 삼축비 영역에서 파단을 표현 할 수 있는 파단 변형률을 정식화하였으며 이를 식 (14)와 Fig. 7에 나타내었다.
ABAQUS/Explicit에서 파단 변형률을 정의하기 위한 기본 변수는 변형률속도, 응력 삼축비, 온도의 세 가지 이므로 평균 응력 삼축비를 파단 변형률의 변수로 설정하기 위한 사용자-서브루틴의 개발이 필요하다. Fig. 7에서 볼 수 있듯이 EH36 강재의 평균 응력 삼축비에 따른 파단 변형률은 무차원 임계 에너지 100% 수준에 근사하며, 이 파단 변형률 곡선을 상용 유한요소 프로그램 ABAQUS/Explicit 사용자-서브루틴에 이식하였다. 사용자-서브루틴은 포트란(Fortran)을 이용하여 개발되었다.
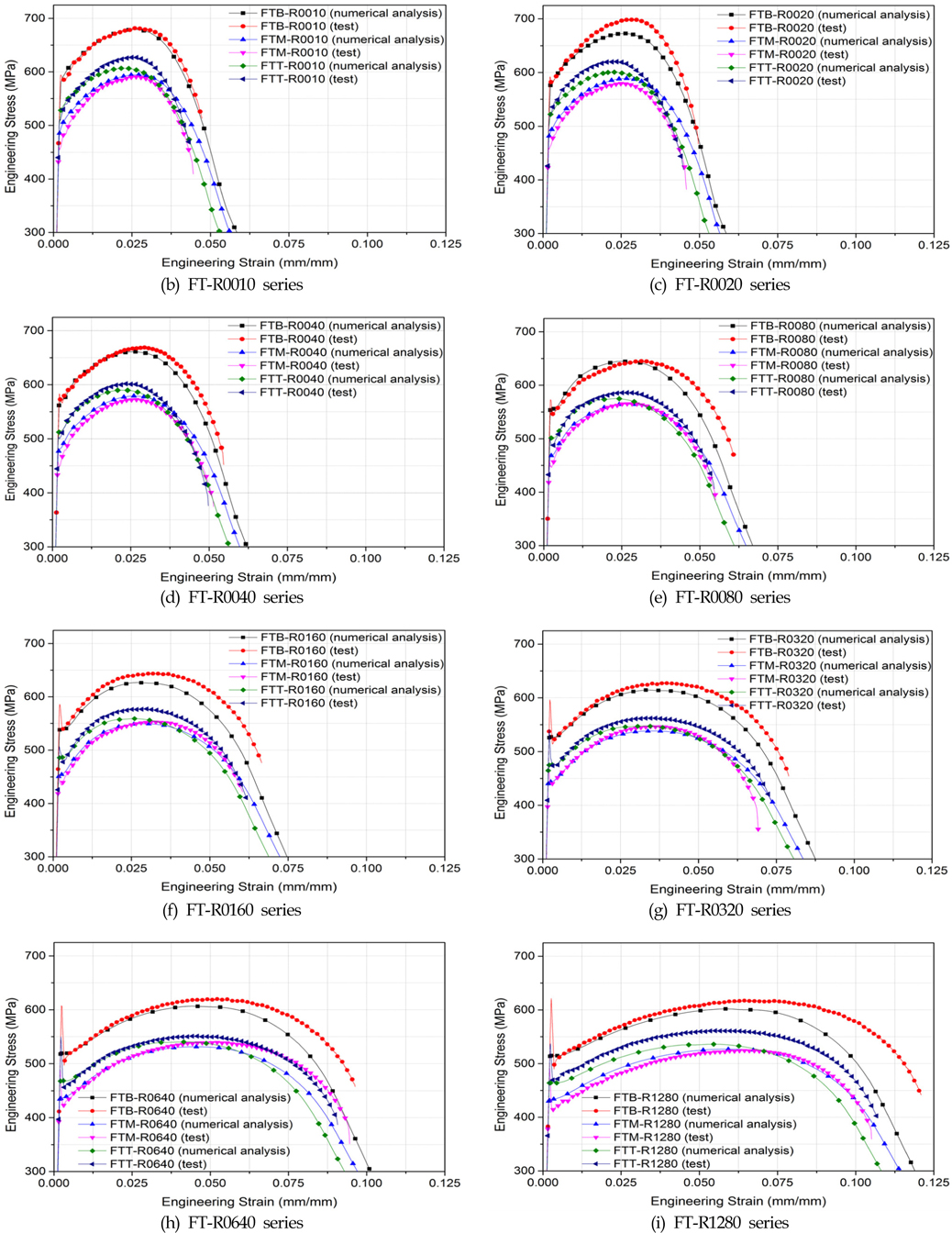
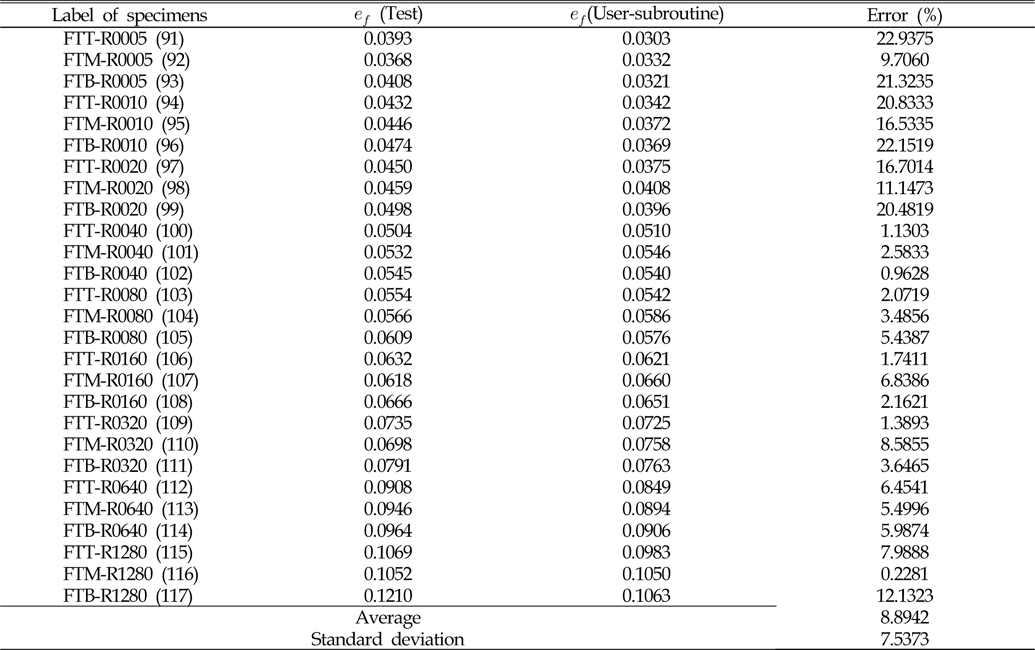
정식화된 파단 변형률 곡선이 노치재의 파단을 정확하게 예측하는지 확인하기 위하여, Table 1에 나타낸 노치 시편을 대상으로 ABAQUS/Explicit 사용자-서브루틴을 이용하여 비선형 유한요소해석이 수행되었다. Fig. 8은 실험 및 수치해석에서 얻은 공칭응력-공칭변형률 곡선을 비교하여 나타내었는데, 가독성을 높이기 위하여 일부 시편에 대하여만 나타내었다. 대신 Table 3-5에 공칭 파단 변형률(
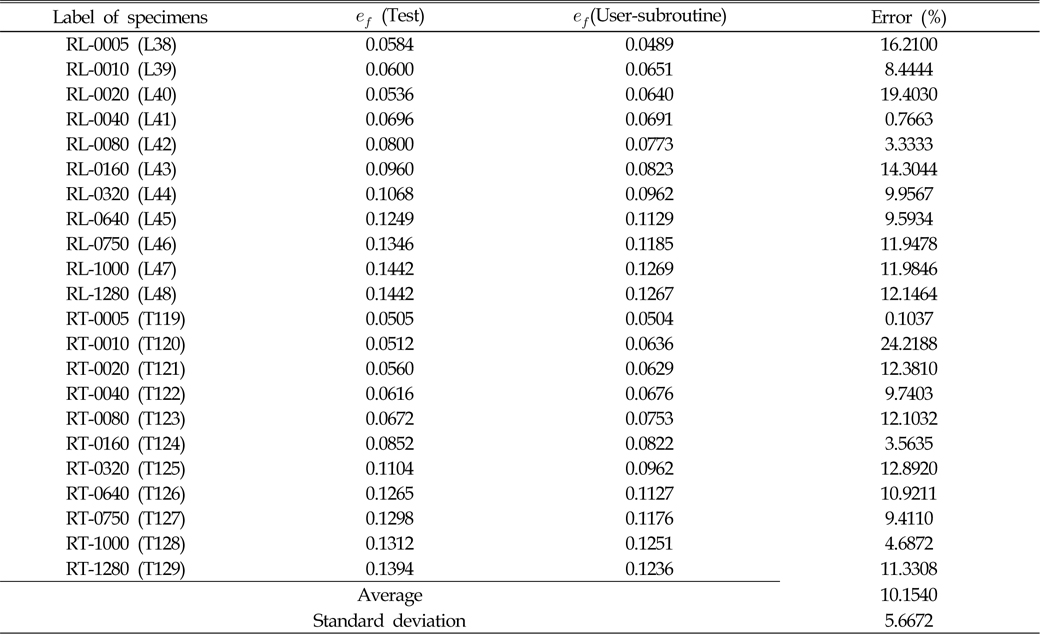
[Table 3] Comparison of engineering failure strain for round bar specimens
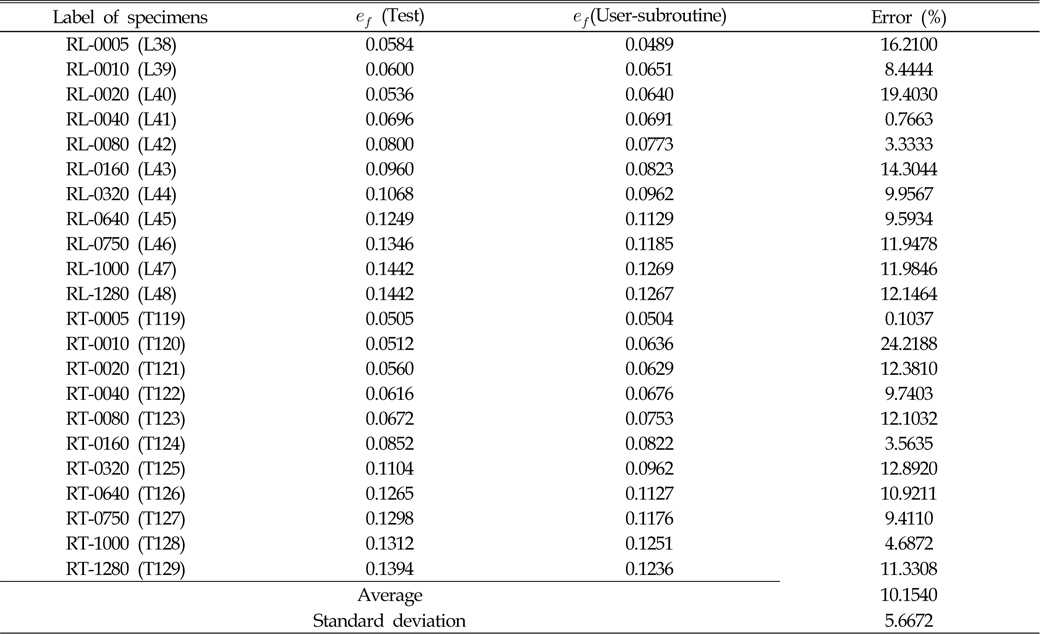
Comparison of engineering failure strain for round bar specimens
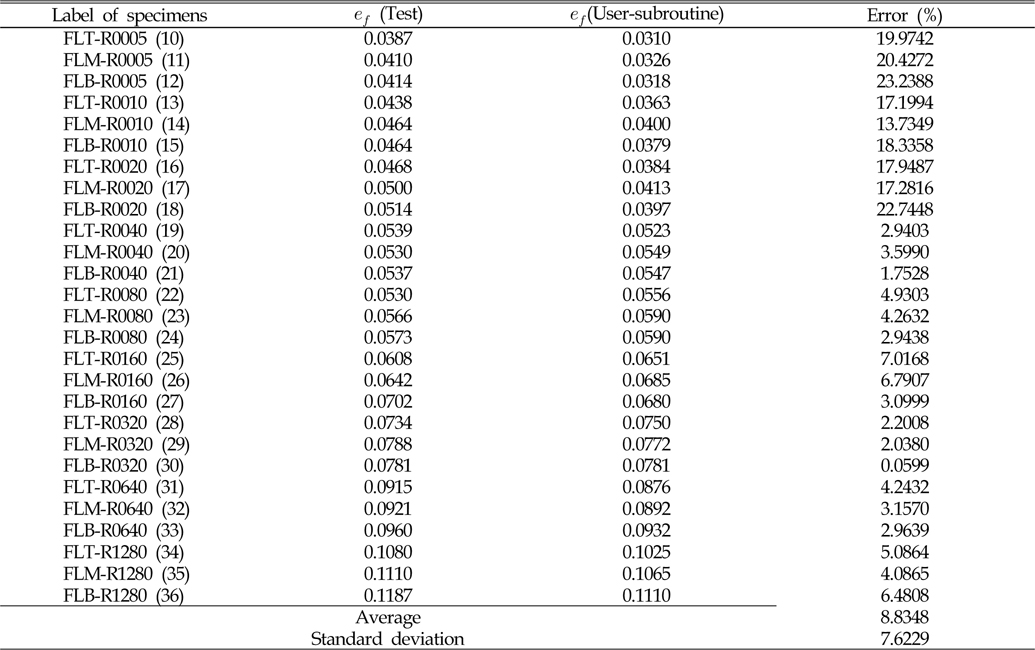
Comparison of engineering failure strain for flat bar specimens (rolling-parallel direction)
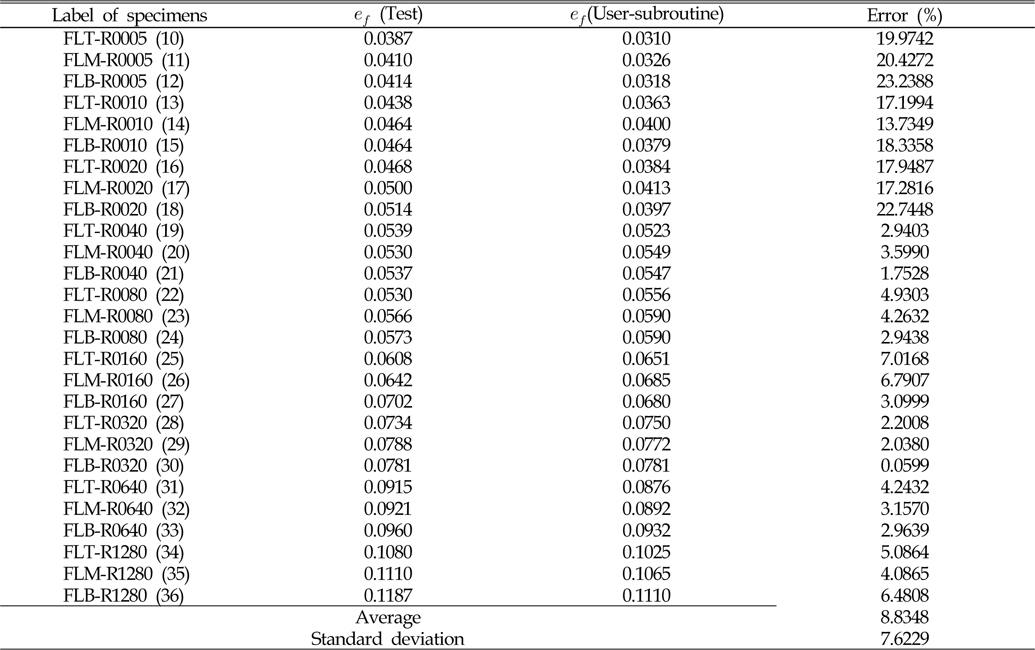
[Table 5] Comparison of engineering failure strain for flat bar specimens (rolling-normal direction)
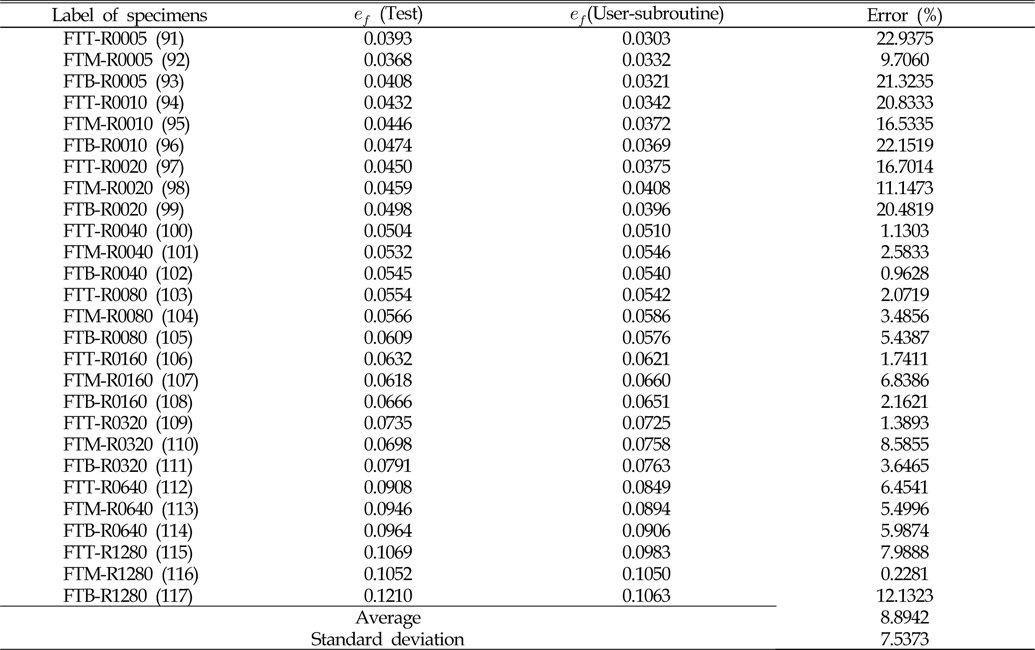
Comparison of engineering failure strain for flat bar specimens (rolling-normal direction)
본 논문에서는 기존에 Choung et al.(2011) 및 Choung and Nam(2013)에 의하여 제시된 결과와 함께 새로운 실험을 실시하여 낮은 응력삼축비 영역에 적용될 새로운 파단 변형률 곡선을 정식화하였다. 이를 위하여 재료의 파단 변형률을 평균 응력삼축비의 함수로서 표현하고 EH36 강재의 인장 실험 및 수치해석을 실시하였다. 새로운 실험은 서로 다른 노치를 가지는 판상형 노치재에 대하여 실시되었다. 수치해석 시 필요한 유동응력을 얻기 위해 평활재의 균일 진응력 곡선을 도출하고 네킹 이후의 대변형률 구간에서 비선형적인 진응력 선도를 고려하여 수정 진응력을 유동응력으로 사용하였다.
시편의 인장실험으로부터 얻은 공칭응력-공칭 변형률 곡선을 수치해석과 비교한 결과 수치해석이 높은 신뢰성을 갖고 있음을 확인하였다. 이후 수치해석과 실험 결과를 비교하여 파단 시점을 확인할 수 있었고 파단이 시작되는 지점에서의 정수압 응력, von Mises 응력을 도출하여 평균 응력 삼축비를 계산하였다. 파단 시점에서의 등가 소성 변형률을 파단 변형률로 정의하여 평균 응력 삼축비에 따른 파단 변형률 관계를 얻을 수 있었으며, 이에 대한 곡선 적합을 통하여 낮은 평균 응력 삼축비 영역에서 파단 변형률을 직선으로 정식화하였다.
이렇게 얻어진 파단 변형률 곡선을 재료의 파단 조건으로 사용하기 위하여 ABAQUS/Explicit 사용자-서브루틴을 개발하였다. 사용자-서브루틴의 타당성을 검증하기 위하여 노치재 시편의 인장 파단 시뮬레이션을 실시하였고, 공칭 응력-변형률선도의 비교 및 공칭 파단 변형률의 비교를 통하여 개발된 사용자-서브루틴의 유효성을 검증할 수 있었다.
수치해석 결과를 실험 결과와 비교하면, 대부분의 노치재 시편에서 파단의 개시점이 유사하였지만, 일부 환봉형 시편과 매우 작은 노치 반지름을 가지는 판상형 시편의 경우 상이한 결과를 보이기도 하였다. 이를 정밀하게 규명하기 위해서는 로드각이 파단 변형률 곡선에 포함될 필요가 있으며, 이를 위해서 전단 응력 또는 압축 응력 등이 지배적인 실험이 수행되어야 한다.