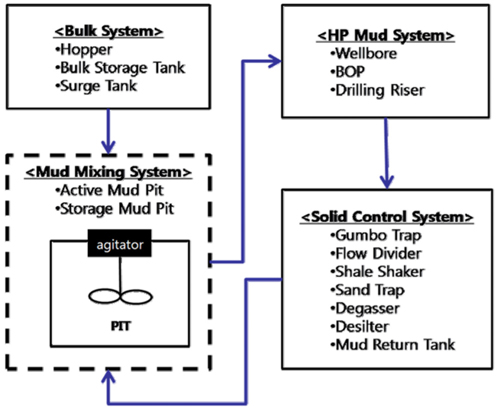
최근의 해양플랜트 설비는 EPC(Engineering, procurement and construction)의 형태로 수주를 하는 경향이 크게 증가하고 있다. EPC사업은 넓은 분야의 엔지니어링을 수행하여야 하며 여기에 CFD(Computational fluid dynamics)와 같은 컴퓨터 시뮬레이션 기술을 다방면으로 활용하고 있다. 드릴쉽, 반잠수식 시추선 등의 시추설비는 시추 시에 유정의 함몰이나 붕괴를 방지하기 위한 목적의 드릴링 유체로 머드를 사용하며 Fig. 1과 같은 머드 순환 시스템이 구비된다(An and Oh, 2012). 머드는 바라이트(Barite), 벤토나이트(Bentonite) 등을 포함하고 시추설비에 탑재된 머드 탱크에서 혼합 및 저장되었다가 머드 펌프를 이용하여 드릴 비트에 공급된다. 이때, 머드를 일정한 밀도, 점도로 혼합하여 드릴 파이프에 주입하므로 머드 탱크에서 내부 순환 및 혼합이 지속적으로 이루어져야 한다(Guo and Liu, 2011). 해양플랜트의 특성상 머드 탱크는 일반적인 교반 설비에 비하여 대형이며 2개 이상의 다축 및 다수의 임펠러를 사용하는 경우가 많다. 교반기의 성능을 나타내는 주요한 지표로는 교반에 필요한 소요 동력과 교반되는 혼합 시간이 있다(Edward et al., 2008). 머드 탱크와 같은 교반기의 연구는 다양한 방법으로 진행되고 있으며 최근의 컴퓨터 시뮬레이션 기술의 발달로 CFD를 통한 연구도 활발하게 진행되고 있다.
Edward et al.(2008)은 임펠러의 양수 능력을 나타내는 지표인 플로우 수(Flow number)의 비교검토를 수행하였다. 교반 레이놀즈 수(Reynolds number) 40~10,000의 유동장에 대한 교반기CFD해석과 LDV(Laser doppler velocimetry)실험을 수행하여 플로우 수가 잘 일치함을 보였다(Edward et al., 2004; Chhabra and Richardson, 2008). 본 연구에서는 다상유동해석을 통하여 머드탱크 내부의 교반기 회전 방향에 따른 유체력을 계산하여 소요되는 동력을 추정하였고 혼합 시간을 추정하여 설계검증을 수행하고자 하였다. 또, 이를 통하여 다축 및 다수의 임펠러를 사용해야 하는 경우의 효율적인 구동방식에 대한 검토를 수행하였다.
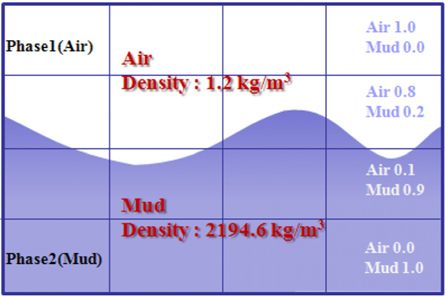
머드 탱크의 비정상유동 해석을 수행하기 위해 슬라이딩 격자법과 VOF(Volume of fluid)법을 이용하였다. 슬라이딩 격자법은 회전체의 회전을 직접 반영하기 위한 해석 기법이고 VOF 법은 2상 유동 해석을 위한 기법이다. 머드 탱크 내부 유동을 해석하기 위한 3차원 비압축성 점성유동을 표현하는 지배방정식을 식 (1) ~ 식 (4)와 같이 나타내었다. 이들은 각각 질량 보존 및 운동량 보존을 표현하는 것으로 일반적인 Navier-Stokes 방정식을 표현하는 것이다.
연속 방정식(Mass conservation law)
여기서 𝜌는 밀도,
운동량 방정식(Momentum conservation law)
여기서,
공기와 머드 사이의 자유수면을 추적하기 위하여 식 (5)와 같은 연속방정식 형태의 체적분율(Volume fraction)에 대한 추가 방정식을 구성한다. 상간의 질량 전달 및 생성을 무시하는 경우 해당 항은 0이다. 본 논문에서는 범용 유동해석 프로그램인 ANSYS Fluent 15.0을 사용하였으며 ANSYS Fluent에서는 제1상을 제외한 상에 대하여 방정식을 풀고 식 (6)과 같이 셀에서 의 체적분율이 1이 되도록 계산하는 방법을 사용한다. Fig. 2에식 (6)의 이미지를 표시하였다(Kolev, 2011; ANSYS, 2013).
여기서
교반기의 성능을 나타내는 지표 중 하나는 혼합 시간이 있다. 교반기가 내부 유체를 잘 섞어주는지를 판단하기 위하여 혼합 시간을 측정하였다. 혼합 시간을 측정하기 위하여 머드에 가상의 추적 입자를 분포시키고 이를 추적하여 체적분율이 일정하게 수렴하는 시간을 혼합 시간으로 판단하였다. 식 (7)은 추적 입자의 수송 방정식이다. 결국, 상기 기본 방정식에 임의의 스칼라 함수를 하나 더 추가하는 것으로 혼합 시간을 추정할 수 있다.
여기서
문제를 간단히 하기 위하여 식 (7)에서 확산항을 제거하였다. 확산항을 제거하여 모델링한 근거는 식 (8)에 나타낸 바와 같이 페클레수(Pecklet number)를 기준으로 하였다.
여기서
일반적인 액체의 확산계수는 10–9정도이기 때문에
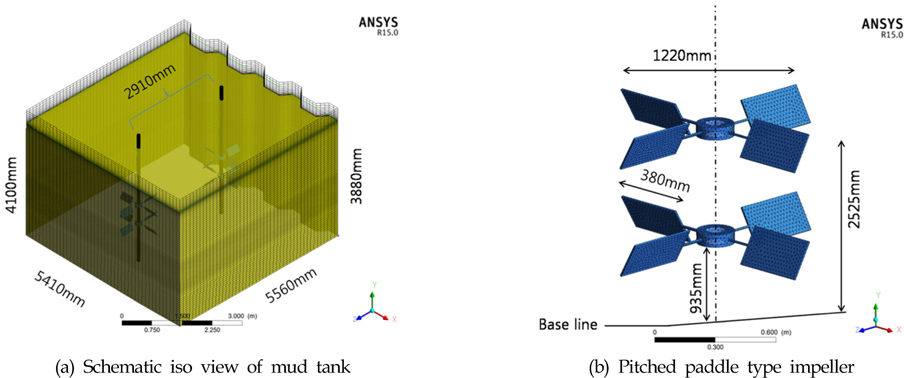
본 논문에서 사용한 머드 탱크의 형상과 임펠러를 Fig. 3에 나타내었다. 탱크의 바닥면에는 x방향으로 약간의 경사를 배치하였는데 이는 실제 사용하는 선체의 형상을 그대로 모사한 것이다. 탱크내부에는 2개의 축을 사용하여 교반하고 있으며 각 축에는 4장의 블레이드로 구성된 2개의 임펠러로 구성되어 있다.
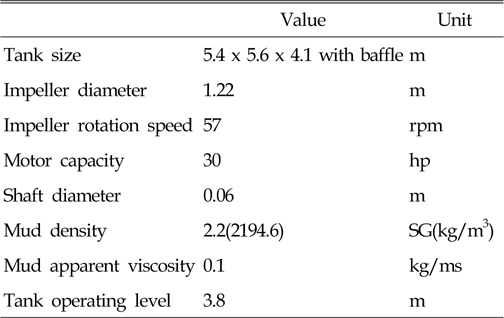
본 논문에서 다루고자하는 머드는 실제 시추선에서 사용하고 있는 물성을 참고하여 뉴턴 유체로 가정하였고 탱크의 제원 및 계산에 사용한 머드의 물성 등의 주요한 제원은 Table 1과 같다. 머드 유동층은 상대적으로 낮은 농도에서는 의가소성 유체의 거동을 보이나, 고농도에서는 빙햄(Bingham) 소성유체의 거동을 보이는 비뉴턴 유체이다(Nguyen et al., 2012). 본 논문에서는 소요 동력의 산정에 주요하게 영향을 미치는 것이 회전수와 임펠러 직경이며 회전방향의 영향을 비교 평가하는 것이 주요한 목적이기 때문에 머드를 점도의 변화가 없는 뉴턴유체로 가정하였다.
[Table 1] Geometric data and mud properties
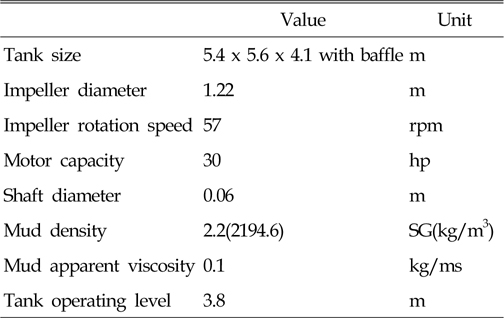
Geometric data and mud properties
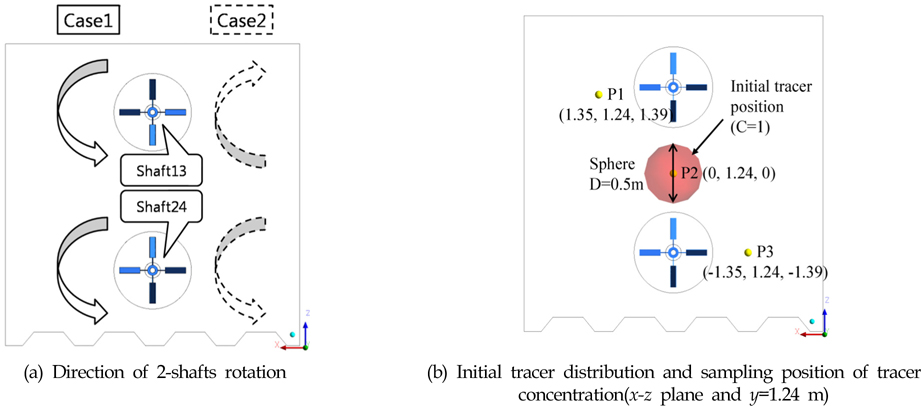
Fig. 4는 머드 탱크의 평면도를 나타내고 있다. 본 논문에서 비교 검토하고자 하는 것은 Shaft13, Shaft24로 명명된 두 개의 축이 동일하게 반시계방향으로 회전하는 경우(Case 1: co-rotating case)와 각각 시계방향과 반시계방향으로 회전하는 경우(Case 2: counter-rotating case)의 횡력, 축력, 토크 등의 유체력을 계산하여 교반에 필요한 소요 동력을 추정하고 혼합 시간을 비교 검토하였다. Case 2의 반대방향으로 회전하는 Shaft 13은 블레이드의 피치도 회전방향에 맞게 수정하여 계산하였다. 여기에 CFD에 의한 소요 동력의 추정치를 비교하기 위하여 Nagata 등이 제안한 상관식으로 소요 동력을 산정하였고 각 케이스와 상관식의 소요 동력을 비교하였다(Japan Society for Chemical Engineers, 2011). 혼합 시간을 추정하기 위한 추적 입자는 Fig. 4(b)와 같이 머드체적의 0.52%를 초기 배치하였다.
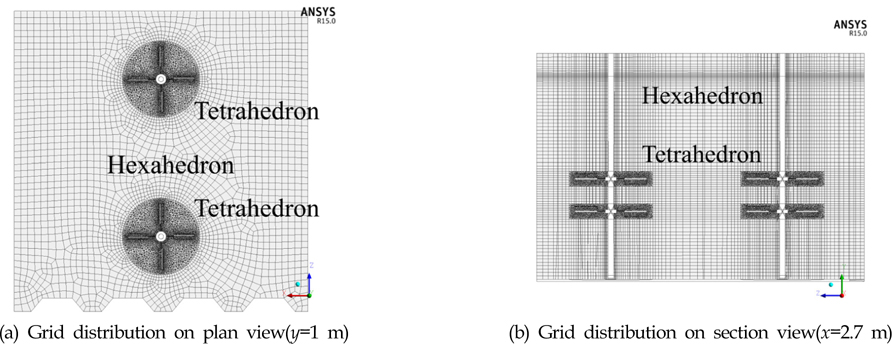
Fig. 5는 본 논문에서 사용한 격자를 나타내고 있다. 교반기의 회전부인 축을 포함한 임펠러는 4면체(Tetrahedron) 타입의 격자를 적용하고 나머지 비회전부의 머드 탱크 영역은 6면체(Hexahedron) 타입의 격자로 수렴성을 고려하였다. 해석에 사용한 전체 격자수는 약 80만개이다. 회전부와 비회전부가 만나는 접촉면은 해석의 안정성을 위해서 비슷한 비율로 변화하도록 하였다.
Table 2에 본 논문에서 사용한 수치 계산 방법을 나타내었다. 운동에 따른 내부 유체의 거동을 파악하기 위하여 비정상 해석을 수행하였고 해석의 안정적인 압력-속도 커플링을 위해 PISO 법을 사용하였다. 그 외에 공간 이산화에는 2차정도의 고차정도 스킴을 사용하였으며 수렴판정 조건 등은 ANSYS Fluent의 기본값을 사용하였다.
[Table 2] Multi-phase simulation settings
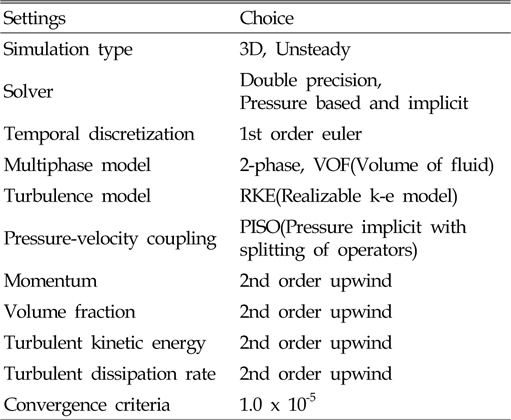
Multi-phase simulation settings
통상 교반조는 상관식으로 추정하여 설계한다. 교반기의 직경, 방해판의 수, 회전수와 같은 기본 사양을 바탕으로 필요한 동력을 예측한다. 본 논문에서는 상관식으로 추정한 동력을 기준 값으로 회전 방향에 따라서 소요 동력은 어느 정도 차이가 나는지 확인하였다. 교반동력을 결정할 때 사용하는 무차원 수는 교반 레이놀즈 수와 동력 수이다(Edward et al., 2008). 교반기의 소요 동력은 액체의 용량 및 점성, 교반기의 회전수, 교반기 임펠러의 종류 이외에도 교반조의 형상 및 방해판과 같은 다양한 변수가 적용되기 때문에 엄밀하게 실험 및 해석을 통하여 산정하여야 한다. 고전적인 방법으로는 Nagata 등이 제시한 상관식으로 추정할 수 있다(Japan Society for Chemical Engineers, 2011). 식 (9)는 교반 레이놀즈 수이고, 식 (10)은 동력 수이다. 식 (11)의 교반 동력을 나타내는 식은 식(9), 식 (10) 을 이용하여 구할 수 있다. 식 (11)로부터 동력을 산정하거나 식(12)를 이용하여 실험 시에 토크 메타로 읽은 토크 값 혹은 CFD해석에 의한 토크를 이용하여 산정할 수 있다. 여기에, 식(13)은 Nagata 등이 제안한 동력수를 구하기 위한 상관식이다. 여기서 구한 동력수 또한 식 (11)을 이용하여 소요 동력을 계산하였다.
여기서 𝜌는 밀도,
여기서
상관식을 이용한 동력 계산에는 교반조의 형상 및 방해판을 가정하여 계산하였다. 0.24m의 폭을 가지는 방해판을 4장 가정하였고 교반조는 직경 3.6m의 원통형으로 가정하여 계산한 후 두 개의 축 값으로 환산하였다. 식 (13)의 상관식으로 추정한 동력수
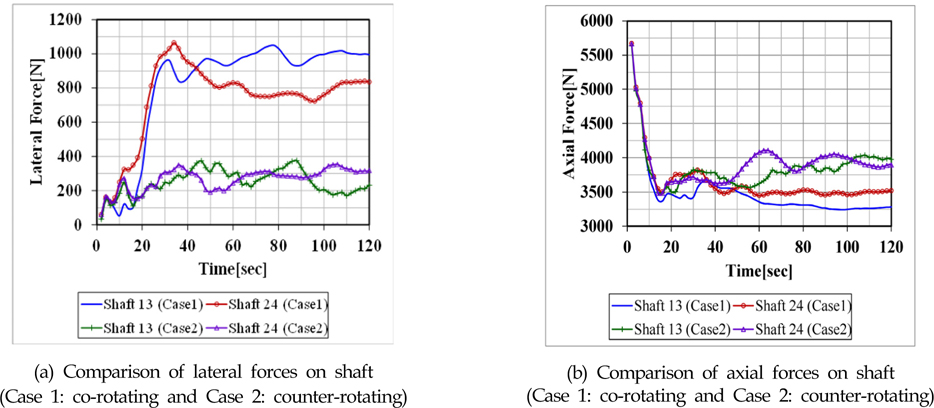
Fig. 6은 CFD해석을 통하여 계산된 횡력과 축력을 비교한 것이다. Case 2에 비하여 Case 1의 횡력의 절대값이 크다. 이는 Case 1이 축계의 진동에 취약하다는 의미로 볼 수 있다. Case 2 의 경우, 하나의 대칭형 임펠러가 회전할 경우 마주보는 블레이드에 가해지는 유체력에 의한 항력이 서로 상쇄되어 축에 횡력이 발생하지 않는 것으로 판단된다. 축력은 두가지 케이스 모두 비슷한 수준이지만 Case 2가 약 500N정도 큰 값으로 Case 1에 비하여 더 오래 진동하고 있음을 알 수 있다. 운전의 관점에서 보면 두 개의 축을 서로 다른 방향으로 회전시키는 것 보다 같은 방향으로 회전시키는 것이 축의 진동 방지의 측면에서 유리 하다고 판단된다.
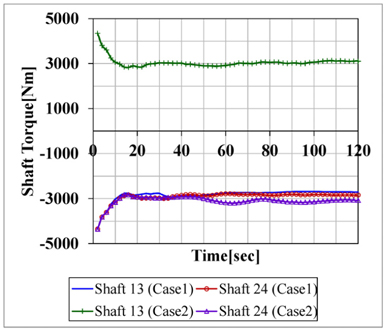
Fig. 7은 각 축에 걸리는 토크이다. Case 2의 경우 Shaft13이 반시계방향으로 회전하고 있다. 이 토크 값은 식 (12)를 이용하여 소요동력으로 환산할 수 있다.
Table 3에 두 가지 케이스에서 계산되어진 토크를 이용하여 환산한 소요 동력을 표시하였다. 서로 반대로 회전하는 Case 2가 대략 12%(3.7 kW)의 동력을 더 필요로 하는 것을 알 수 있다.
[Table 3] Comparison of power consumption

Comparison of power consumption
운전의 관점에서 보면 두 개의 축을 서로 다른 방향으로 회전시키는 것보다 같은 방향으로 회전시키는 것이 소요 동력의 측면에서도 유리하다고 판단된다.
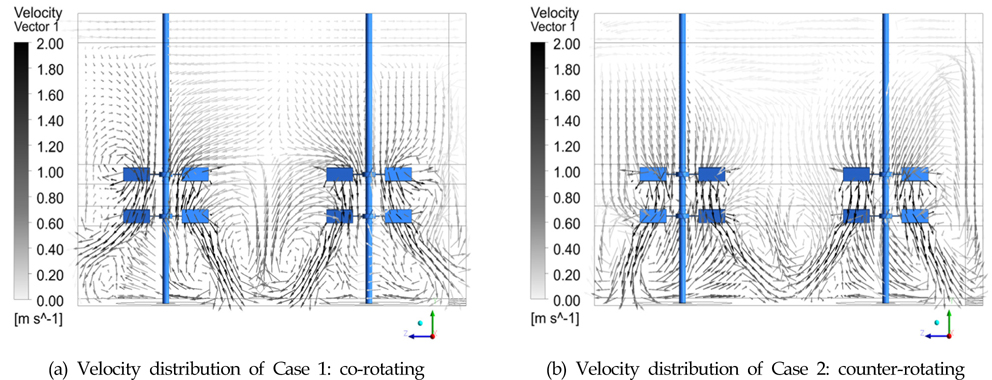
Fig. 8은 축 중앙의
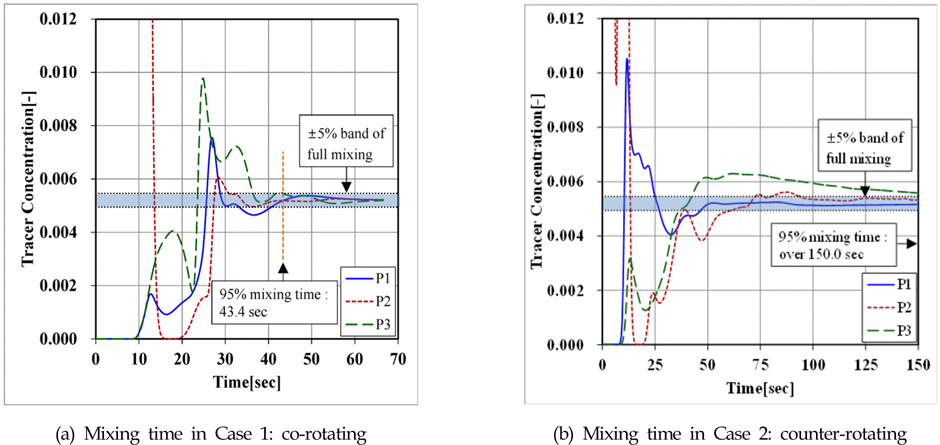
Fig. 9는 두 가지 케이스의 혼합 시간을 나타내고 있다. Fig. 4(b)에 나타낸 것과 같이 전체 체적의 0.52%의 농도에 해당하는 추적 입자를 초기 분포하였기 때문에 각 계측 포인트의 추적입자의 농도는 0.52%로 수렴해야 한다. Fig. 9는 농도 0.52%의 95%인 0.494%까지 수렴하는 시간을 측정한 것으로 Case 1이 Case 2에 비하여 혼합 시간이 약 100초 이상 짧다. 운전의 관점에서 보면 두 개의 축을 서로 다른 방향으로 회전시키는 것보다 같은 방향으로 회전시키는 것이 유동장 혼합의 측면에서 유리하다고 판단된다.
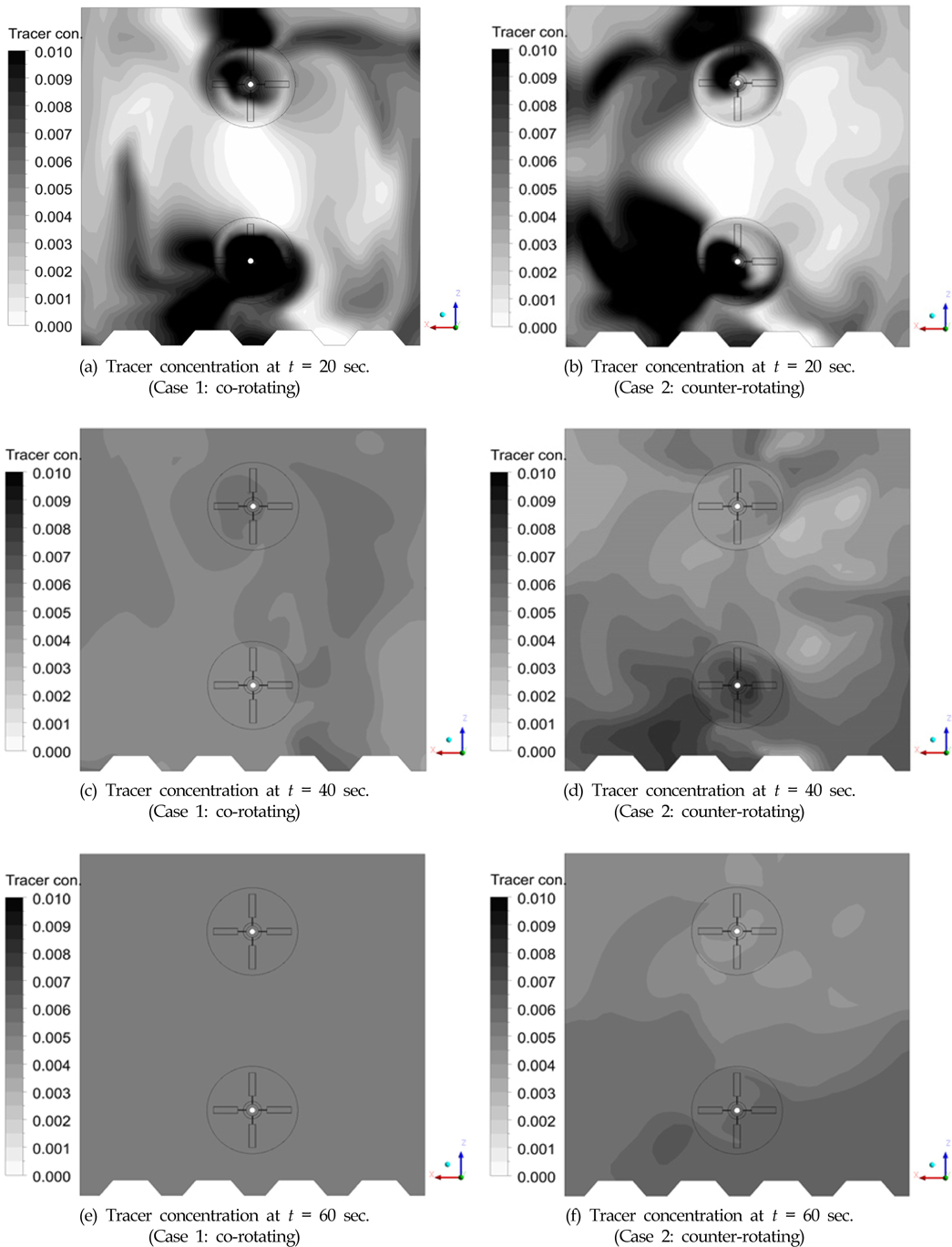
Fig. 10은 초기분포 후 각 20초, 40초, 60초에서 추적 입자의 농도 분포를 나타내고 있다. Fig. 10(a), (c), (e)는 Case 1의 분포이고 Fig. 10(b), (d), (f)는 Case 2의 분포이다. Case 1은 60초에 균등한 분포를 보이는 것에 비해 Case 2는 균등한 분포를 이루기 위해서는 더 많은 시간 동안 혼합이 이루어져야 한다는 것을 알 수 있다. Case 2와 같이 두 축이 서로 반대방향으로 회전하는 경우 방해판 측에 농도차가 큰 것으로 미루어 짐작하면 방해판이 혼합에 악영향을 미치는 것으로 판단된다.
본 논문에서는 머드 탱크에서 서로 다른 두 개의 축의 회전 방향에 따른 유체력, 소요 동력, 유동 패턴, 혼합 시간 등의 교반기의 성능을 검토하였다. 이상의 검토결과, 두 개의 축을 사용하는 경우의 회전방향에 대한 종합적인 평가는 축의 회전방향은 같은 방향으로 일치시키는 것이 유리하다는 결론에 도달했다.
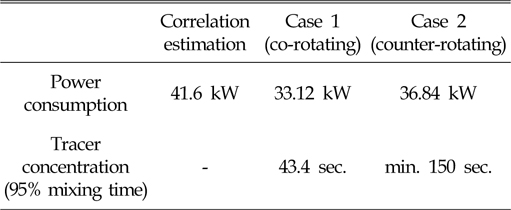
Table 4에 나타낸 것과 같이 머드 탱크의 주요 성능지표인 교반 소요 동력과 혼합 시간에 대하여 다음과 같은 상세 결론을 얻을 수 있다.
[Table 4] Power consumption and mixing time
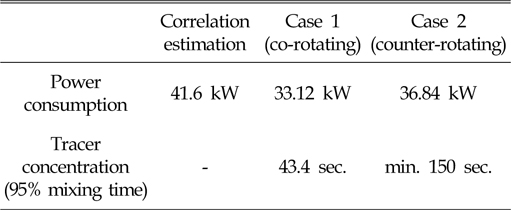
Power consumption and mixing time
(1) 서로 다른 두 개의 축을 사용하는 경우 운전의 측면에서 서로 반대 방향으로 회전시키는 것보다는 동일한 방향으로 회전시키는 것이 소요 동력의 약 10% 적게 소비하는 것을 알 수 있다. 또한, 상관식으로 추정한 소요 동력은 약 25% 정도 높은 값으로 추정되었다.
(2) 서로 다른 두 개의 축을 사용하는 경우 운전의 측면에서 서로 반대 방향으로 회전시키는 것보다는 동일한 방향으로 회전시키는 것이 혼합 시간의 측면에서 약 1/3의 시간만 소모하는 것을 알 수 있다.