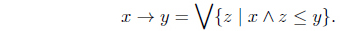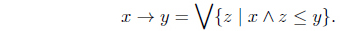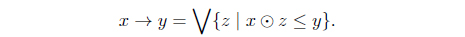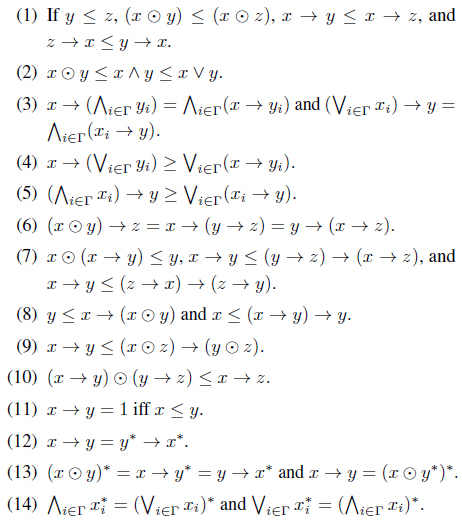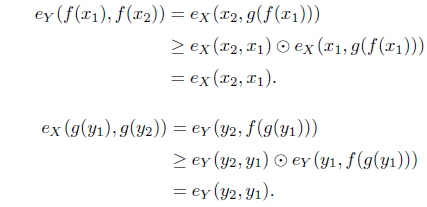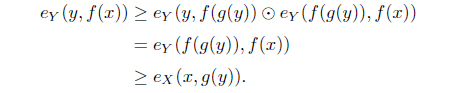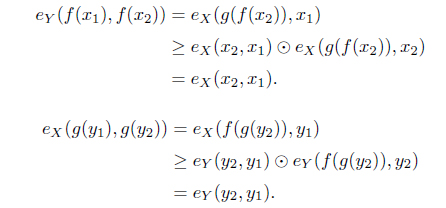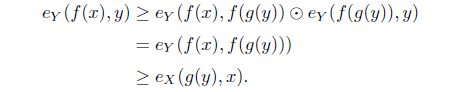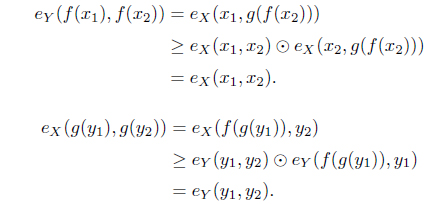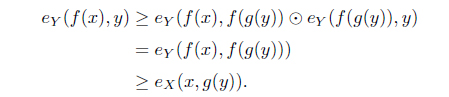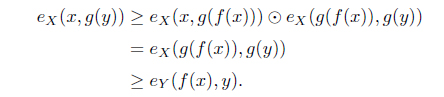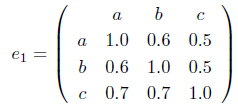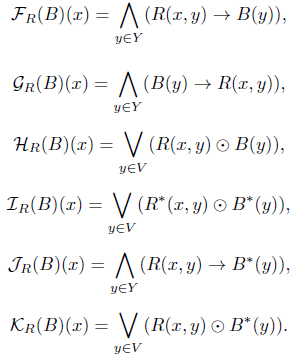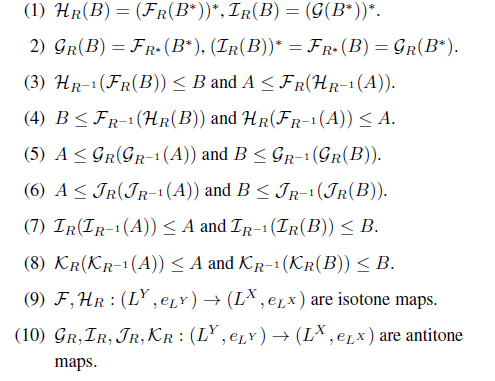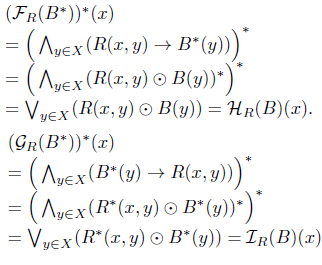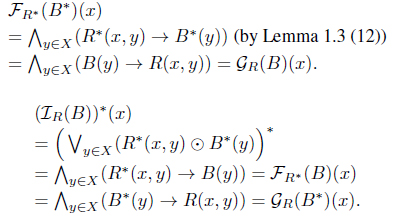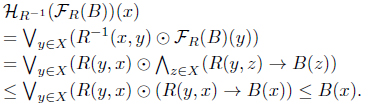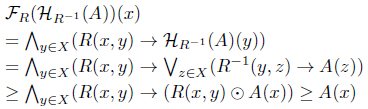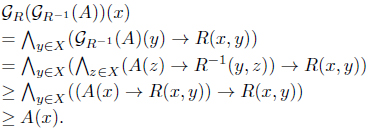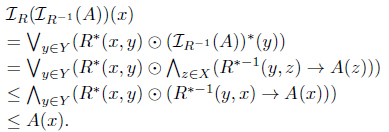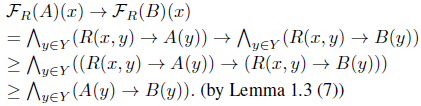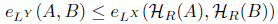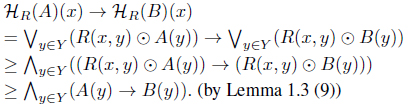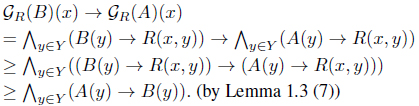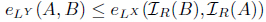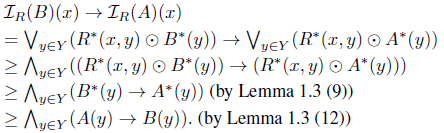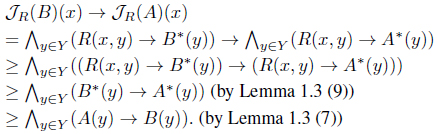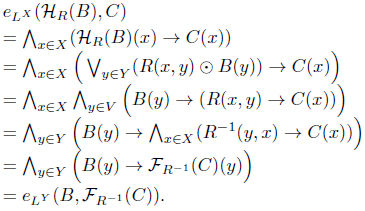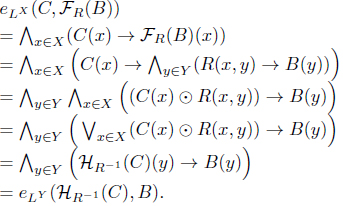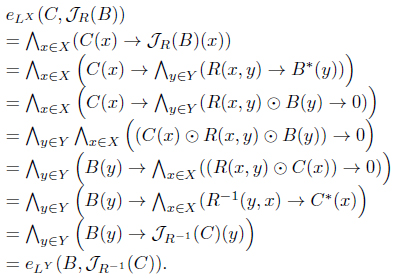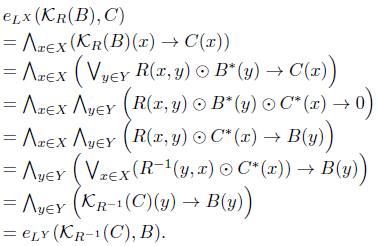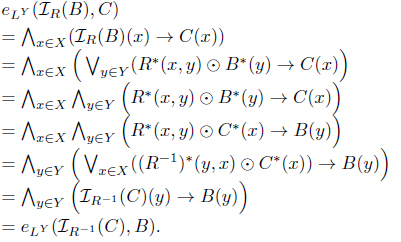A Galois connection is an important mathematical tool for algebraic structure, data analysis, and knowledge processing [1-10]. Hájek [11] introduced a complete residuated lattice L that is an algebraic structure for many-valued logic. A context consists of (U, V, R), where U is a set of objects, V is a set of attributes, and R is a relation between U and V. Bĕlohlávek [1-3] developed a notion of fuzzy contexts using Galois connections with R ∈ L^X×Y on L.

In this paper, we investigate properties of fuzzy Galois (dual Galois, residuated, and dual residuated) connections in L and give their examples. In particular, we study fuzzy Galois (dual Galois, residuated, and dual residuated) connections induced by L-fuzzy relations.

Definition 1.1. [11, 12] An algebra is called a complete residuated lattice if it satisfies the following conditions:

(C1) is a complete lattice with the greatest element 1 and the least element 0; (C2) (L, , 1) is a commutative monoid; (C3) x y ≤ z iff x ≤ y → z for x, y, z ∈ L.

Remark 1.2. [11, 12] (1) A completely distributive lattice is a complete residuated lattice defined by

In particular, the unit interval is a complete residuated lattice defined by

(2) The unit interval with a left-continuous t-norm , , is a complete residuated lattice defined by

In this paper, we assume that is a complete residuated lattice with the law of double negation, i.e., a = a** where a = a → 0.

Lemma 1.3. [12] For each x, y, z, x_i, y_i ∈ L, we have the following properties.

Definition 1.4. [4, 7] Let X denote a set. A function e_X : X × X → L is called:

(E1) reflexive if eX(x, x) = 1 for all x ∈ X, (E2) transitive if eX(x, y) eX(y, z) ≤ eX(x, z), for all x, y, z ∈ X, and (E3) if eX(x, y) = eX(y, x) = 1, then x = y.

If e satisfies (E1) and (E2), (X, e_X) is a fuzzy preorder set. If e satisfies (E1), (E2), and (E3), (X, e_X) is a fuzzy partially order set (for simplicity, fuzzy poset).

Example 1.5. (1) We define a function

e_Lx : L^X × L^X → L

as

e_Lx(A, B) = (A(x) → B(x)).

Then, (L^X, e_Lx) is a fuzzy poset from Lemma 1.3 (10, 11).

(2) If (X, e_X) is a fuzzy poset and we define a function (x, y) = e_X(y, x), then (X, ) is a fuzzy poset.

Definition 2.1. Let (X, e_X) and (Y, e_Y) denote fuzzy posets and f : X → Y and g : Y → X denote maps.

(1) (e_X, f, g, e_Y) is called a Galois connection if for all x ∈ X, y ∈ Y,

eY(y, f(x)) = eX(x, g(y)).

(2) (e_X, f, g, e_Y) is called a dual Galois connection if for all x ∈ X, y ∈ Y,

eY(f(x), y) = eX(g(y), x).

(3) (e_X, f, g, e_Y) is called a residuated connection if for all x ∈ X, y ∈ Y,

eY(f(x), y) = eX(x, g(y)).

(4) (e_X, f, g, e_Y) is called a dual residuated connection if for all x ∈ X, y ∈ Y,

eY(y, f(x)) = eX(g(y), x).

(5) f is an isotone map if e_Y(f(x₁), f(x₂)) ≥ e_X(x₁, x₂) for all x₁, x₂ ∈ X.

(6) f is an antitone map if e_Y(f(x₁), f(x₂)) ≥ e_X(x₂, x₁) for all x₁, x₂ ∈ X.

(7) f is an embedding map if e_Y(f(x₁), f(x₂)) = e_X(x₁, x₂) for all x₁, x₂ ∈ X.

If X = Y and e_X = e_Y, we simply denote (e_X, f, g) for (e_X, f, g, e_Y). (X, (e_X, f, g)) is called a Galois (resp. residuated, dual Galois, and dual residuated) pair.

Remark 2.2. Let (X, e_X) and (Y, e_Y) denote a fuzzy poset and f : X → Y and g : Y → X denote maps.

(1) (eX, f, g, eY) is a Galois (resp. dual Galois) connection iff (eY, g, f, eX) is a Galois (resp. dual Galois) connection. (2) (eX, f, g, eY) is a Galois (resp. residuated) connection iff (, f, g, ) is a dual (resp. dual residuated) Galois connection. (3) (eX, f, g, eY ) is a residuated (resp. dual residuated) connection iff (, g, f, ) is a residuated (resp. dual residuated) connection. (4) (eX, f, g, eY) is a Galois (resp. dual Galois) connection iff (eX, f, g, ) is a residuated (resp. dual residuated) connection. (5) (eX, f, g, eY) is a residuated connection iff (eY, g, f, eX) is a dual residuated connection.

Theorem 2.3. Let (X, e_X) and (Y, e_Y) denote a fuzzy poset and f : X → Y and g : Y → X denote maps.

(1) (eX, f, g, eY) is a Galois connection if f, g are antitone maps and eY(y, f(g(y))) = eX(x, g(f(x))) = 1. (2) (eX, f, g, eY) is a dual Galois connection if f, g are antitone maps and eY(f(g(y)), y) = eX(g(f(x)), x) = 1. (3) (eX, f, g, eY) is a residuated connection if f, g are isotone maps and eY(f(g(y)), y) = eX(x, g(f(x))) = 1. (4) (eX, f, g, eY) is a dual residuated connection if f, g are isotone maps and eY(y, f(g(y))) = eX(g(f(x)), x) = 1.

Proof. (1) Let (f, g) denote a Galois connection. Since

e_Y(y, f(x)) = e_X(x, g(y)),

we have

1 = e_Y(f(x), f(x)) = e_X(x, g(f(x)))

and

e_Y(y, f(g(y))) = e_X(g(y), g(y)) = 1.

Furthermore,

Conversely,

Similarly, e_Y(y, f(x)) ≤ e_X(x, g(y)).

(2) Since e_Y(f(x), y) = e_X(g(y), x), we have

1 = e_Y(f(x), f(x)) = e_X(g(f(x)), x)

and

e_Y(f(g(y)), y) = e_X(g(y), g(y)) = 1.

Furthermore,

Conversely,

Similarly, e_Y(f(x), y) ≤ e_X(g(y), x).

(3) Since e_Y(f(x), y) = e_X(x, g(y)), we have

1 = e_Y(f(x), f(x)) = e_X(x, g(f(x)))

and

e_Y(f(g(y)), y) = e_X(g(y), g(y)) = 1.

Furthermore,

Conversely,

Moreover,

(4) It is similarly proved as (3).

Example 2.4. Let X = {a, b, c} denote a set and f : X → X denote a function as f(a) = b, f(b) = a, f(c) = c. Define a binary operation (called Łukasiewicz conjunction) on L = [0, 1] using

x y = max{0, x + y − 1},

x → y = min{1 − x + y, 1}.

(1) Let (X = {a, b, c}, e₁) denote a fuzzy poset as follows:

Since e₁(x, y) = e₁(f(x), f(y)),

e₁(x, f(f(x))) = e₁(f(f(x)), x) = 1,

then, (e₁, f, f) are both residuated and dual residuated connections. Since 0.7 = e₁(c, a) e₁(f(a, f(c)) = e₁(b, c) = 0.5, f is not an antitone map. Hence, (e₁, f, f) are neither Galois nor dual Galois connections.

(2) Let (X = {a, b, c}, e₂) denote a fuzzy poset as follows:

Since e₂(x, y) = e₂(f(y), f(x)),

e₂(x, f(f(x))) = e₂(f(f(x)), x) = 1,

then, (e₂, f, f) are both Galois and dual Galois connections. Since 0.7 = e₂(c, a) e₂(f(c), f(a)) = e₂(c, b) = 0.5, f is not an isotone map. Hence, (e₂, f, f) are neither residuated nor dual residuated connections.

Definition 2.5. Let R ∈ L^X×Y denote a fuzzy relation. For each A ∈ L^X and B ∈ L^Y, we define operations R⁻¹(y, x) = R(x, y) and : L^Y → L^X as follows:

Theorem 2.6. Let R ∈ L^X×Y denote a fuzzy relation. For each A ∈ L^X and B ∈ L^Y,

Proof. (1) From Lemma 1.3 (13,14), we have

(2)

(3) From Lemma 1.3 (7), we have

From Lemma 1.3 (8), we have

(4) From Lemma 1.3 (8), we have

(6)

(7)

(9) from:

(10) from:

Similarly, from:

Other cases are similarly proved.

Theorem 2.7. Let R ∈ L^X×Y denote a fuzzy relation, (L^X, e_Lx) and (L^Y, e_Lʏ) denote fuzzy posets. We have the following properties.

(1) and are residuated connections.

(2) and are dual residuated connections.

(3) and are Galois connections.

(4) and are dual Galois connections.

Proof. (1) For each C ∈ L^X, B ∈ L^Y,

(2) For each C ∈ L^X, B ∈ L^Y,

(3) For each C ∈ L^X, B ∈ L^Y,

(4) For each C ∈ L^X, B ∈ L^Y,

For each C ∈ L^X, B ∈ L^Y,

Other cases are similarly proved.

In this paper, we investigated the properties of fuzzy Galois (dual Galois, residuated, and dual residuated) connections in a complete residuated lattice L. In particular, we studied fuzzy Galois (dual Galois, residuated, and dual residuated) connections induced by L-fuzzy relations.

In the future, we will investigate the properties using fuzzy connections on algebraic structures and study the fuzzy concept lattices.

No potential conflict of interest relevant to this article was reported.