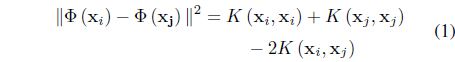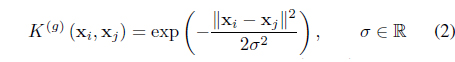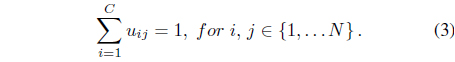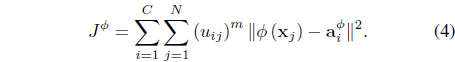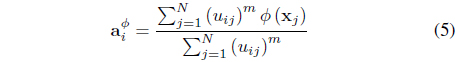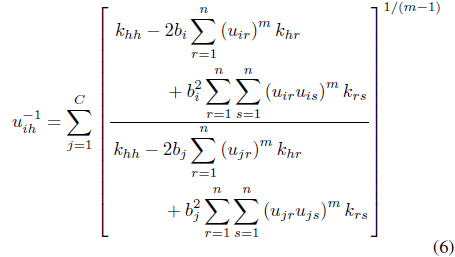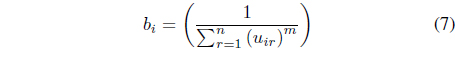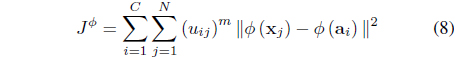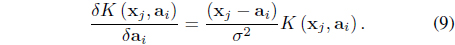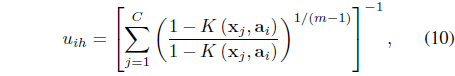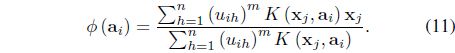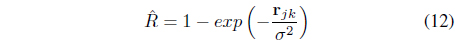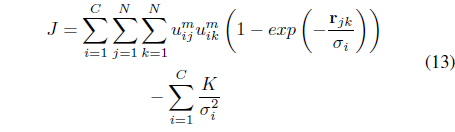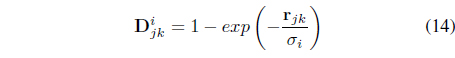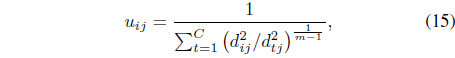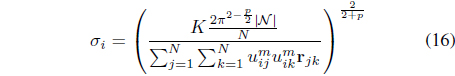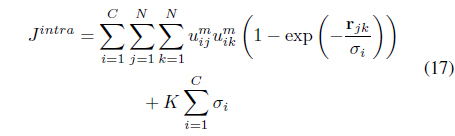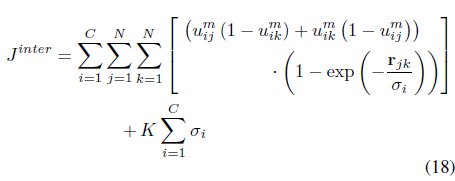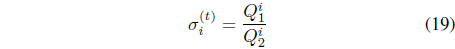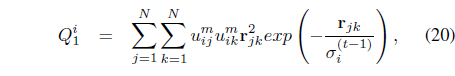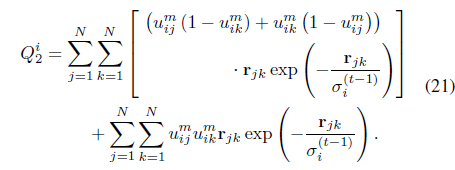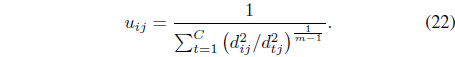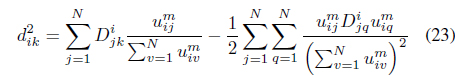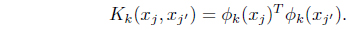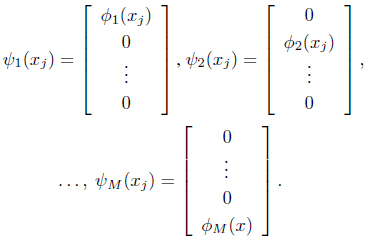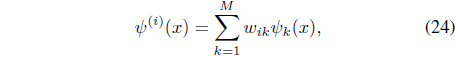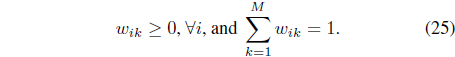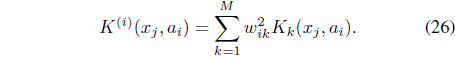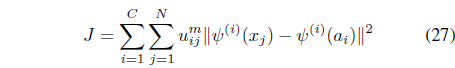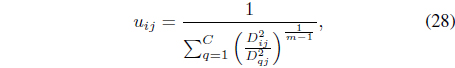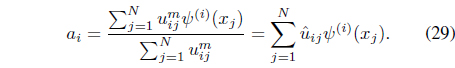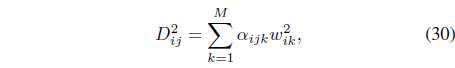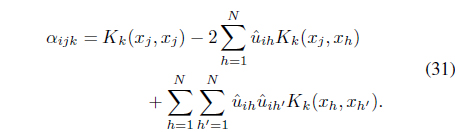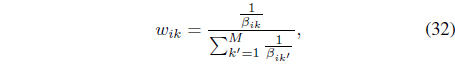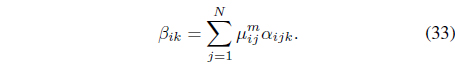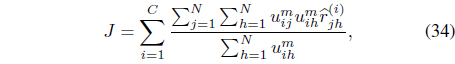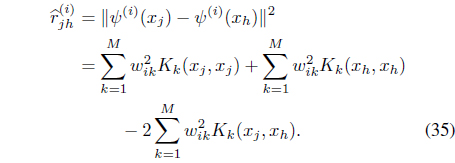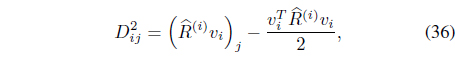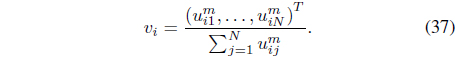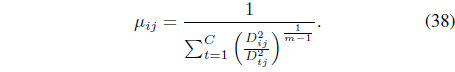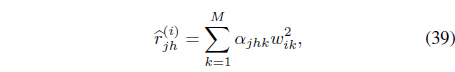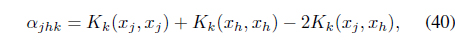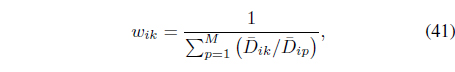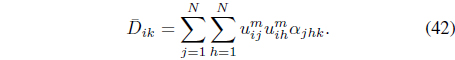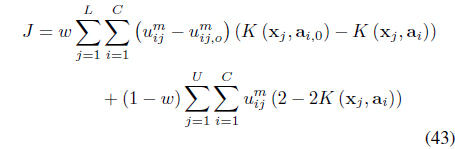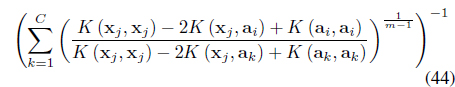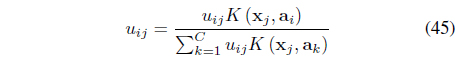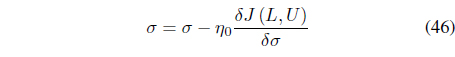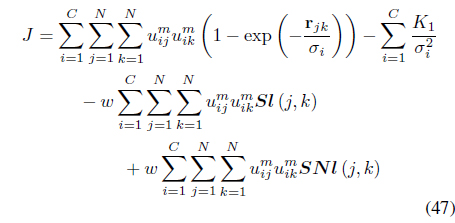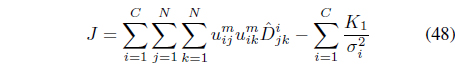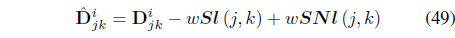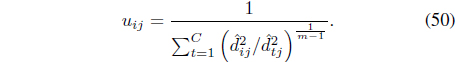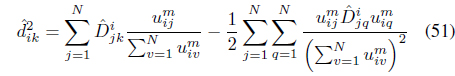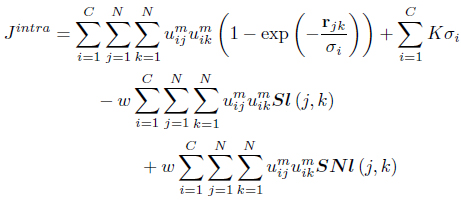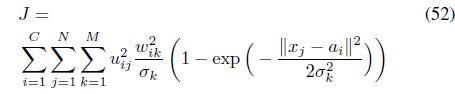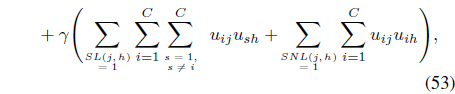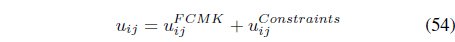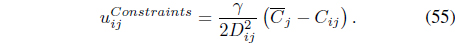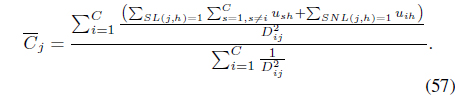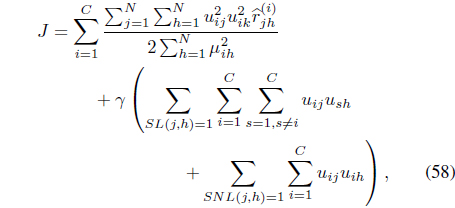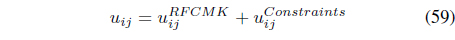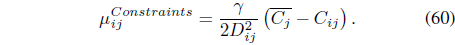Clustering is an essential and frequently performed task in pattern recognition and data mining. It aids in a variety of tasks related to understanding and exploring the structure of large and high dimensional data. The goal of cluster analysis is to find natural groupings in a set of objects such that objects in the same cluster are as similar as possible and objects in different clusters are as dissimilar as possible.

In most applications, categories are rarely well separated and boundaries are overlapping. Describing these real world situations by crisp sets does not allow the user to quantitatively distinguish between objects which are strongly associated with a particular category from those that have only a marginal association with multiple ones, particularly, along the overlapping boundaries. Fuzzy clustering methods are good at dealing with these situations. In fact, data elements can belong to more than one cluster with fuzzy membership degrees.

Fuzzy clustering is widely used in the machine learning field. Areas of application of fuzzy cluster analysis include data analysis [1, 2], information retrieval [3, 4], image segmentation [5], and robotics [6]. One of the most widely used fuzzy clustering algorithm is the fuzzy C-means (FCM) algorithm [7].

Typically, the data to be clustered could have an object based or a relational based representation. In object data representation, each object is represented by a feature vector, while for the relational representation only information about how two objects are related is available. Relational data representation is more general in the sense that it can be applied when only the degree of dissimilarity between objects is available, or when groups of similar objects cannot be represented efficiently by a single prototype.

Despite the large number of existing clustering methods, clustering remains a challenging task when the structure of the data does not correspond to easily separable categories, and when clusters vary in size, density, and shape. Kernel based approaches [8-14] can adapt a specific distance measure in order to make the problem easier. They have attracted great attention and have been applied in many fields such as fault diagnosis of marine diesel engine [12], bridge parameters estimation [13], watermarking [14], automatic classiffication fragments of ceramic cultural relics [15], image segmentation [16], model construction for an erythromycin fermentation process [17], oil-immersed transformer fault diagnosis [18], analyzing enterprises independent innovation capability in order to promote different strategies [19], segmentingmagnetic resonance imaging brain images [20, 21], and classification of audio signals [22].

Kernel clustering approaches rely on their ability to produce nonlinear separating hyper surfaces between clusters by performing a mapping ϕ from the input space X to a high dimensional feature space F. One of the most relevant aspects in kernel applications is that it is possible to compute Euclidean distances in F without knowing it explicitly. This can be done using the distance kernel trick [23]:

In Eq. (1), K (x_i, x_j) = Φ (x_i)^T Φ (x_j) is the Mercer Kernel [24]. Gaussian kernels,

are the most commonly used ones.

In this paper, we survey existing fuzzy kernel clustering algorithms. We provide an overview of unsupervised algorithms as well as semi-supervised algorithms that integrate partial supervision into the objective function to guide the optimization process. For most algorithms, we describe the objective function being optimized and the necessary conditions to optimize it. We also highlight the advantages and disadvantages of the different methods.

Let {x₁, ··· , x_N} be a set of N data points to be partitioned into C clusters, and R = [r_jk] is a relational matrix where r_jk represents the degree to which pairs of objects x_j and x_k are related. The matrix R could be given or it could be constructed from the features of the objects. Each object x_j belongs to every cluster i with a fuzzy membership u_ij that satisfies [7]:

0 ≤ u_ij ≤ 1,

and

The exponent m ∈ (1, ∞) is a constant that determines the level of cluster fuzziness.

The FSK-FCM algorithm [25] derives a kernel version of the FCM in the feature space by minimizing

subject to Eq. (3). In Eq. (4), is the center of cluster i, in the feature space, defined as:

Minimization of Eq. (4) with respect to u_ij yields [25]

where

The FSK-FCM algorithm is one of the early kernel versions of the FCM. It is simple and has the flexibility of incorporating different kernels. It achieves this by simply fixing the update equation for the centers in the feature space. Thus, since this equation is not derived to optimize the objective function, there is no guarantee that the obtained centers are optimal. Morevover, in [25] the authors use Gaussian kernels with one global scale (𝜎) for the entire data. The selection of this parameter is not discussed in [25].

The MK-FCM [26] is an extension of the FSK-FCM that allows the cluster centers to be optimized. It minimizes

subject to the constraint in Eq. (3). In Eq. (8), ϕ (a_i) is the center of cluster i in the feature space F. Minimization of Eq. (8) has been proposed only for the case of a Gaussian kernel using the fact that

In this case, it can be shown [26] that the update equations for the memberships and centers are

and

Unlike the FSK-FCM, the MK-FCM learns the optimal cluster centers in the feature space. However, the update equations have been derived only for the case of Gaussian kernels with one fixed global scale.

The FSK-FCM and MK-FCM are object based algorithms and require an explicit feature representation of the data to be clustered. The kNERF algorithm [27], on the other hand, is a kernelized version of the non-Euclidean relational FCM algorithm [28], and works on relational data. kKERF does not formulate a new objective function. It simply uses a Gaussian kernel to compute a relational similarity matrix R = [r_jk] using

Then, it uses the non-Euclidean relational fuzzy (NERF) C-means [28] to cluster .

kNERF is not a true kernel clustering algorithm. It simply uses kernels as a preprocessing step to create the similarity matrix. Since this step is not part of the optimization process, any kernel function can be used. However, this also prevents the kernel parameters from being optimized for the given data. Also, kNERF constructs a relational matrix with one global Gaussian parameter for the entire data. The selection of this parameter is discussed in [27] but there has been no attempt to devise methods to automatically select it.

Although good results were obtained using the Gaussian kernel function, its performance depends on the selection of the scale parameter. Moreover, since one global 𝜎 is used for the entire data set, it may not be possible to find one optimal parameter when there are large variations between the distributions of the different clusters in the feature space. One way to learn optimal Gaussian parameters is through an exhaustive search of one parameter for each cluster. However, this approach is not practical since it is computationally expensive especially when the data include a large number of clusters and when the dynamic range of possible values for these parameters is large. Moreover, it is not trivial to evaluate the resulting partition in order to select the optimal parameters. To overcome this limitation, the LSL algorithm [29] has been proposed. It minimizes one objective function for both the optimal partition and for cluster dependent Gaussian parameters that reflect the intra-cluster characteristics of the data. The LSL algorithm minimizes

subject to the membership constraint in Eq. (3). The first term in Eq. (13) seeks compact clusters using a local relational distance, , with respect to each cluster i. This distance is defined as

where the scaling 𝜎_i controls the rate of decay of as a function of the distance between x_j and x_k with respect to cluster i. The cluster dependent 𝜎_i allows LSL to deal with the large variations, in the feature space, between the distributions and the geometric characteristics of the different clusters. The second term in Eq. (13) is a regularization term to avoid the trivial solution where all the scaling parameters 𝜎_i are infinitely large.

Optimization of J with respect to u_ij and 𝜎_i yields the following update equations [29]:

and

where |𝒩| is the cardinality of the neighborhood of j.

In Eq. (16), 𝜎_i is inversely proportional to the intra-cluster distances with respect to cluster i. Thus, when the intra-cluster dissimilarity is small, 𝜎_i is large allowing the pairwise distances over the same cluster to be smaller and thus, obtain a more compact cluster. On the other hand, when the intra-cluster dissimilarity is high, 𝜎_i is small to prevent points which are not highly similar from being mapped to the same location. According to Eq. (16), 𝜎_i can also be seen as the average time to move between points in cluster i.

LSL has the advantages of learning cluster dependent resolution parameters and can be used to idenify clusters of various densities. However, this also makes the optimization process more complex and prone to local minima. Moreover, the partition generated by LSL depends on the choice of the constant K in Eq. (13).

FLeCK [30] is an extension of LSL that does not assume that K is fixed. It learns the scaling parameters and K by optimizing both the intra-cluster and the inter-cluster dissimilarities. Consequently, the learned scale parameters reflect the relative density, size, and position of each cluster with respect to the other clusters. In particular, FLeCK minimizes the intra-cluster distances

and maximizes the inter-cluster distances

The constant K provides a way of specifying the relative importance of the regularization term (second term in Eqs. (17) and 18)), compared to the sum of intra-cluster (first term in Eq. (17)) and inter-cluster distances (first term in Eq. (18)). The parameter, 𝜎_i, controls the rate of decay of . This approach learns a cluster dependent 𝜎_i in order to deal with the large variations between the distributions and the geometric characteristics of each cluster.

Using the Lagrange multiplier technique and assuming that the values of 𝜎_i do not change significantly from one iteration (t − 1) to the next one (t), it can be shown [30] that

where

and

The simultaneous optimization of Eqs. (17) and (18) with respect to u_ij yields [30]:

where

and is as defined in Eq. (14).

LSL [29] and FLeCK [30] have the advantage of learning cluster dependent scaling parameters. Thus, they can be used to identify clusters of different densities. However, these algorithms have two main limitations. First, learning 𝜎_i for each cluster involves complex optimization and is prone to local minima. Second, data points assigned to one cluster are constrained to have one common density. An alternative approach, that involves relatively simpler optimization, and overcomes the above limitations is based on multiple kernel learning (MKL) [31-34]. Instead of using one kernel (fixed or learned) per cluster, MKL uses multiple kernels for each cluster.

Most existing MKL methods assume that kernel weights remain constant for all data (i.e., space-level), while algorithms like Localized MKL [35] seek kernel weights that are data dependent and locally smooth (i.e., sample-level). Although sample-level non-uniform methods give the largest flexibility, in practice relaxations are typically introduced to enhance tractability. Most of the previous MKL approaches have focused on supervised [32, 33] and semi-supervised learning [35]. Recently, an extension of multiple kernels to unsupervised learning, based on maximum margin clustering, was proposed in [36]. However, this method is only designed for crisp clustering. In [37], Huang et al. designed a multiple kernel fuzzy clustering algorithm which uses one set of global kernel weights for all clusters. Therefore, their approach is not appropriate for clusters of various densities. To overcome these drawbacks, Baili and Frigui proposed the FCMK [38]. FCMK is based on the observation that data within the same cluster tend to manifest similar properties. Thus, the intra-cluster weights can be approximately uniform while kernel weights are allowed to vary across clusters.

Given a set of M embedding mappings that map the data to new feature spaces, Φ = {ϕ1, . . . , ϕ_M}. Each mapping ϕ_k maps the p-dimensional data x as a vector ϕ_k(x) in its feature space whose dimensionality is L_k. Let {K₁, . . . , K_M} be the kernels corresponding to these implicit mapping respectively,

Since these implicit mappings do not necessarily have the same dimensionality, the authors in [38] construct a new set of independent mappings, Ψ = ｛ψ₁; ψ₂; ... ; ψ_M｝, from the original mappings Φ as

Each of these constructed mappings converts x into an L- dimensional vector, where . The linear combination of the bases in Ψ within each cluster i is defined as

with

A new cluster-dependent kernel, K⁽ⁱ⁾, between object j and cluster i, is computed as a convex combination of M Gaussian kernels K₁, K₂, . . . , K_M with fixed scaling parameters 𝜎₁, 𝜎₂, . . . , 𝜎_M, respectively. That is,

In Eq. (26), W = [w_ik], where w_ik ∈ [0; 1] is a resolution weight for kernel K_k with respect to cluster i. A low value of w_ik indicates that kernel K_k is not relevant for the density estimation of cluster i (due to its scaling parameter), and that this kernel should not have a significant impact on the creation of this cluster. Similarly, a high value of w_ik indicates that the bandwidth of kernel K_k is highly relevant for the density estimation of cluster i, and that this kernel should be the main factor in the creation of this cluster.

The FCMK algorithm minimizes

subject to the constraints in Eqs. (3) and (25). It can be shown [38] that minimization of Eq. (27) with respect to u_ij yields

where D_ij denotes the distance between data x_j and cluster center a_i, i.e., . Similarly, minimization of Eq. (27) with respect to a_i yields

where is the normalized membership.

Using Eq. (29), the distance between data x_j and cluster center a_i can be written as

where the coefficients α_ijk are defined as

Replacing Eq. (30) back in Eq. (27) and introducing a Lagrange multiplier, the optimal kernel weights need to be updated using

where

The FCMK is based on the MK-FCM [26] and inherits the limitations of object-based clustering. First, multiple runs of the algorithm may be needed since it is susceptible to initialization problems. Second, FCMK is restricted to data for which there is a notion of center (centroid). Finally, FCMK is not suitable for all types of data. For instance, the density is estimated by counting the number of points within a specified radius, 𝜎_k, of the cluster center. However, for data with multiple resolutions within the same cluster, density should take into account variance between pairs of points and not points to center.

To overcome the limitations of FCMK, the RFCMK was proposed in [39]. The RFCMK involves dissimilarity between pairs of objects instead of dissimilarity of the objects to a cluster center. It minimizes

subject to the constraints in Eqs. (3) and (25). In Eq. (34), is the transformed relational data between feature points x_j and x_h, with respect to cluster i define using the implicit mapping ψ⁽ⁱ⁾:

The distance from feature vector x_j to the center of the i^th cluster, a_i, can be written in terms of the relational matrix using [40]

where υ_i is the membership vector defined by

It can be shown [39] that optimiation of Eq. (34) with respect to u_ij yields

Rewriting the relational data Eq. (35) as

where

it can be shown [39] that the kernel weights need to be updated using

where

In Eq. (41), the resolution weight w_ik is inversely proportional to α_jhk, which is the distance between objects x_j and x_h induced by kernel k. When, the objects are mapped close to each other, w_ik will be large indicating that kernel k is relevant. On the other hand, when, the objects are mapped far apart, the weight w_ik will be small indicating that kernel k is irrelevant.

Clustering is a difficult combinatorial problem that is susceptible to local minima, especially for high dimensional data. Incorporating prior knowledge in the unsupervised learning task, in order to guide the clustering process has attracted considerable interest among researchers in the data mining and machine learning communities. Some of these methods use available side-information to learn the parameters of the Mahalanobis distance (e.g. [41–43]). The Non-linear methods have focused on the kernelization of Mahalanobis metric learning methods (e.g. [44–46]). However, these approaches are computationally expensive or even infeasible for high dimensional data.

Another approach to guide the clustering process is to use available information in the form of hints, constraints, or labels. Supervision in the form of constraints is more practical than providing class labels. This is because in many real world applications, the true class labels may not be known, and it is much easier to specify whether pairs of points should belong to the same or to different clusters. In fact, pairwise constraints occur naturally in many domains.

The SS-KFCM [47] uses L labeled points and U unlabeld points. It assumes that fuzzy memberships can be assigned, using expert knowledge, to the subset of labeled data. Its objective function is defined by adding classification errors of both the labeled and the unlabeled data, i.e.,

The first term in Eq. (43) is the error between the fuzzy centers calculated based on the learned clusters and the labeled information. The second term minimizes the intra-cluster distances. The optimal solutions to Eq. (43) involves learning the fuzzy memberships and the kernel parameters. It can be shown [47] that for the labeled data, the memberships need to be updated using:

u_ij =

and for the unlabeled data, the fuzzy membership need to be updated using:

Optimization of Eq. (43) with respect to 𝜎 does not lead to a closed form expression. Instead, 𝜎 is updated iteratively using:

The SS-KFCM algorithm assumes that a subset of the data is labeled with fuzzy membership degrees. However, for real applications, this information may not be available and can be tedious to generate using expert knowledge. An alternative approach uses pairwise constraints. For the following semisupervised algorithms, we assume that pairwise “Should-Link” constraints (pairs of points that should belong to the same cluster) and “Should not-Link” constraints (pairs of points that should belong to different clusters) are provided with the input. let Sl be the indicator matrix for the set of “Should-Link” pairs of constraints such that Sl (j, k) = 1 means that x_j and x_k should be assigned to the same cluster and 0 otherwise. Similarly, let SNl be the indicator matrix for the set of “Should-Link” pairs such that SNl (j, k) = 1 means that x_j and x_k should not be assigned to the same cluster and 0 otherwise.

The semi-supervised local scaling learning (SS-LSL) [48] minimizes

subject to the constraint in Eq. (3). SS-LSL is an extension of the LSL algorithm [29] that incorporates partial supervision. The second term in Eq. (47), is a reward term for satisfying “Should-Link” constraints and a penalty term for violating “Should not-Link” constraints.

In Eq. (47), the weight w ∈ (0; 1) provides a way of specifying the relative importance of the “Should-Link” and “Should not-Link” constraints compared to the sum of inter-cluster distances. In [48], the authors recommend fixing it as the ratio of the number of constraints to the total number of points.

Setting the derivative of J with respect to 𝜎_i gives the same update equation for 𝜎_i as the LSL algorithm [29] (Refer to Eq. (16)).

The objective function in Eq. (47) can be rewritten as

where

can be regarded as the “effective distance” that takes into account the satisfaction and violation of the constraints.

It can be shown [48] that optimization of J with respect to u_ij yields

where

SS-FLeCK [49] is an extension of FLeCK [30] that incorporates partial supervision information. It attempts to satisfy a set of “Should-Link” and “Should not-Link” constraints by minimizing

The optimal K is determined by simultaneously minimizing the intra-cluster distances Eq. (52) and maximizing the inter-cluster distances in Eq. (18).

It can be shown [49] that optimization of Eq. (52) and Eq. (18) with respect to σ_i yields the same update equation for 𝜎_i as in FLeCK (i.e., Eq. (19)). Similarly, optimization of Eq. (52) with respect to the memberships yields the same update equation as SS-LSL (i.e. Eq. (50)).

The SS-FCMK [50] uses the same partial supervision information to extend FCMK [38] by minimizing:

subject to Eqs. (3) and (25).

In Eq. (53), the weight γ ∈ (0; 1) provides a way of specifying the relative importance of the should-link and should not-link constraints compared to the sum of inter-cluster distances. It can be shown [50] that the update equation for the membership of point x_j to cluster i is

where is given by Eq. (28), and

In Eq. (55), C_ij and are defined as

and

The first term in Eq. (54) is the membership term in the FCMK algorithm and only focuses on distances between feature points and prototypes. The second term takes into account the available supervision: memberships are reinforced or reduced according to the pairwise constraints provided by the user. C_ij is the constraint violation cost associated with feature point x_j if it is assigned to cluster i, while is the weighted average, over all the clusters, of the violation costs associated with feature point x_j . If the violated constraints do not involve feature point x_j , then

Since the constraints in Eq. (53) do not depend on W explicitly, optimization of Eq. (53) with respect to W yields the same update Eq. (32) as in FCMK.

The SS-RFCMK [50] used partial supervision to extend RFCMK [39]. It minimizes

subject to Eqs. (3) and (25).

Using the Lagrange multiplier technique, it can be shown [50] that the memberships need to be updated using

where is as defined in Eq. (38)

In Eq. (60), C_ij and are as defined in Eqs. (56) and (57).

Since the constraints in Eq. (58) do not depend on w_ik explicitly, optimization of Eq. (58) with respect toW yields the same update Eq. (41) as in RFCMK.

In this paper, we have focused on kernel clustering algorithms that are based on the FCM objective function. There are several other fuzzy kernel clustering approaches. For instance, the multisphere support vectors (MSV) clustering [51] extends the SV clustering approach [52]. It defines a cluster as a sphere in the feature space. This yields kernel-based mapping between the original space and the feature space. The kernel possibilistic C-means (KPCM) algorithm [53] applies the kernel approach to the possibilistic C-means (PCM) algorithm [54]. The weighted kernel fuzzy clustering algorithm (WKFCA) [55] is a kernelized version of the SCAD algorithm [56]. It performs feature weighting along with fuzzy kernel clustering. In [57], the authors propose a kernel fuzzy clustering model that extends the additive fuzzy clustering model to the case of a nonlinear model. More specifically, it has been shown that the additive clustering [58] is special case of fuzzy kernel clustering. The similarity structure is then captured and mapped to higher dimensional space by using kernel functions. The kernel fuzzy clustering methods based on local adaptive distances [59] performs feature weighting and fuzzy kernel clustering simultaneously. The sum of the weights of the variables with respect to each cluster is not equal to one as in [55]. However, the product of the weights of the variables for each cluster is constrained be equal to one. The genetic multiple kernel interval type 2 FCM clustering [60] combines heuristic method based on genetic algorithm (GA) and MK-FCM. It automatically determines the optimal number of clusters and the initial centroids in the first step. Then, it adjusts the coefficients of the kernels and combines them in the feature space to produce a new kernel. Other kernel clustering algorithms, based on type 2 fuzzy sets, include [61, 62]. A kernel intuitionistic FCM clustering algorithm (KIFCM) was proposed in [63]. EKIFCM has two main phases. The first one is KIFCM and the second phase is parameters selection of KIFCM with GA. KIFCM is a combination of Atanassov's intuitionistic fuzzy sets (IFSs) [64] with kernel-based FCM (KFCM) [47].

All of the kernel clustering algorithms that we have outlined do not scale to very large (VL) data sets. VL data or big data are any data that cannot be loaded into the computer's working memory. Since clustering is one of the primary tasks used in the pattern recognition and data mining communities to search VL databases in various applications, it is desirable to have clustering algorithms that scale well to VL data.

The scalability issue has been studied by many researchers. In general, there are three main approaches to clustering for VL data: sampling-based methods, incremental algorithms and data approximation algorithms. The sample and extend algorithms apply clustering to a sample of the dataset found by either progressive [65] or random sampling [66]. Then, the sample results are noniteratively extended to approximate the partition for the rest of the data. Representative algorithms include random sample and extend kernel FCM (rseKFCM) algorithm [67] and the random and extend RFCMK (rseRFCMK) [68]. The rseRFCMK is an extension of the RFCMK algorithm to VL data based on sampling followed by non-iterative extension. The main problem with sampling-based methods is the choice of the sample. For instance, if the sample is not representative of the full dataset, then sample and extend methods cannot accurately approximate the clustering solution.

On the other hand, the incremental algorithms are designed to operate on the full dataset by separating it into multiple chunks. First, these algorithms sequentially load manageable chunks of the data. Then, they cluster each chunk in a single pass. They construct the final partition as a combination of the results from each chunk. In [66, 67], a single pass kernel fuzzy C-means (spKFCM) algorithm was proposed. The spKFCM algorithm runs weighted KFCM (wKFCM) on sequential chunks of the data, passing the clustering solution from each chunk onto the next. spKFCM is scalable as its space complexity is only based on the size of the sample. The single pass RFCMK (spRFCMK) [68] is an extension of the RFCMK algorithm to VL data. The spRFCMK is an incremental technique that makes one sequential pass through subsets of the data.

In [66], an online algorithm for kernel FCM (oKFCM) was proposed in which data is assumed to arrive in chunks. Each chunk is clustered and the memory is freed by summarizing the clustering result by weighted centroids. In contrast to spKFCM, oKFCM is not truly scalable and is not recommended for VL data. This is because, rather than passing the clustering results from one chunk to the next, oKFCM clusters the weighted centroids in one final run to obtain the clustering for the entire stream.

Fuzzy kernel clustering has proven to be an effective approach to partition data when the clusters are not well-defined. Several algorithms have been proposed in the past few years and were described in this paper. Some algorithms, such as FSK-FCM, are simple and can incorporate any kernel function. However, these methods impose an intuitive equation to update the centers in the feature space. Thus, there is no guarantee that the optimized objective function of these algorithms correspond to the optimal partition.

Other kernel algorithms can solve for the optimal centers by restricting the kernel to be Gaussian. Some of these algorithms, such as FSK-FCM, use one global scale (𝜎) for all clusters. These are relatively simpler algorithms that are not very sensitive to the initialization. However, they require the user to specify the scale, and may not perform well when the data exhibit large variations between the distributions of the different clusters. Other algorithms, such as FLeCK, use more complex objective functions to learn cluster-dependent kernel resolution parameters. However, because the search space of these methods include many more parameters, they are more prone to local minima. Clustering with multiple kernels is a good compromize between methods that use one fixed global scale and methods that learn one scale for each cluster. These algorithms, such as FCMK, use a set of kernels with different, but fixed, scales. Then, they learn relevance weights for each kernel within each cluster.

Clustering, in general, is a difficult combinatorial problem that is susceptible to local minima. This problem is more acute in Kernel based clustering as they solve the partitioning problem in a much higher feature space. As a result, several semi-supervised kernel clustering methods have emerged. These algorithms incorporate prior knowledge in order to guide the optimization process. This prior knowledge is usually available in the form of a small set of constraints that specify which pairs of points should be assigned to the same cluster, and which ones should be assigned to different clusters.

Scalability to very large data is another desirable feature to have in a clustering algorithm. In fact, many applications involve very large data that cannot be loaded into the computer's memory. In this case, algorithm scalability becomes a necessary condition. We have outlined three main approaches that have been used with kernel clustering methods. These include sampling-based methods, incremental algorithms, and data approximation algorithms.

No potential conflict of interest relevant to this article was reported.