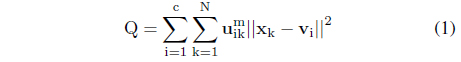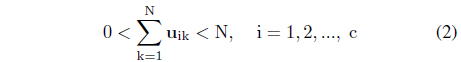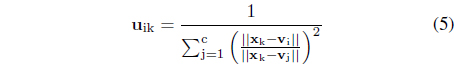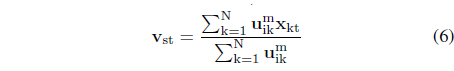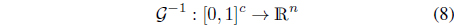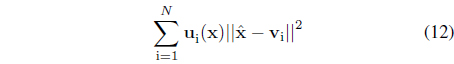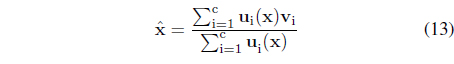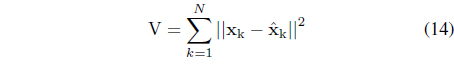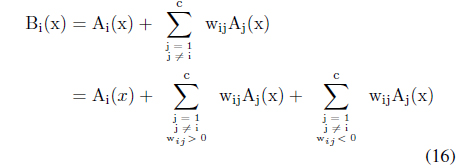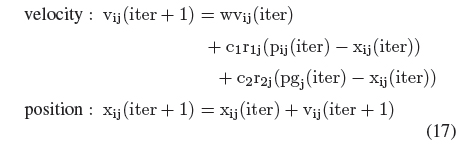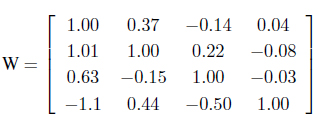Information granules being at the center of granular computing [1, 2] are fundamental concepts using which we perceive, structure and process knowledge in a human-centric fashion. With the ongoing progress witnessed in granular computing, it has become apparent that a number of central problems still deserve our attention including a way of constructing information granules and a process of communication with the external world of data when conveying information granules. The first group of tasks directly relates to clustering and fuzzy clustering. Clustering has been a central conceptual and algorithmic vehicle supporting a realization of information granules. We have witnessed a great deal of developments in this domain [3] including numerous generalizations of clustering methods yielding a formation of higher order granular constructs, see [4] and granular fuzzy clusters [1], in general. There has been a visible role of fuzzy clustering in system modeling [5, 6]. The second problem of communication between the world of numeric data and granular entities revolves around a fundamental concept of the granulation-degranulation mechanism, assessment of its results quantified in terms of so–called degranulation criterion. The quality of information granules is captured by looking in a way how numeric data are granulated and afterwards de-granulated and to which extent a tandem of these two processing phases distorts the data. The distortions are inevitable (with several exceptions which deal with one–dimensional data and engage triangular membership functions, see [1, 7]).

The objective of this study is to further improve the granulation-degranulation abilities by introducing and optimizing transformation of information granules so that the resulting degranulation error becomes minimized. We formulate an overall task as an optimization problem, introduce several categories of transformation functions (realizing suitable interactions/associations among information granules) and discuss the underlying optimization procedures.

The study is organized as follows. We start with a concise review of information granulation realized with the aid of fuzzy clustering (Section 2). The granulation-degranulation idea along with the formal formulation of the problem is presented in Section 3. Section 4 is devoted to the design of interactions among information granules while in Section 5 we provide a number of illustrative experimental studies.

Throughout this study, we consider information granules formed in the n-dimensional space of real numbers, .

Let us briefly recall the underlying concept and ensuing algorithmic aspects of the fuzzy C-means (FCM) algorithm [3, 8], which is one of the commonly used techniques of fuzzy clustering and a computational vehicle to build information granules.

Given is a collection of n-dimensional data (patterns) {x_k|k=1, 2,. . . ,N} where . Our objective is to determine its structure – a collection of “c” clusters (information granules). From the algorithmic perspective, the problem is posed as a minimization of the following objective function (performance index) Q

where v₁,v₂, . . . , v_c are n-dimensional prototypes of the clusters and U = [u_ik] stands for a partition matrix expressing a way of allocation of the data to the corresponding clusters; u_ik is the membership degree of data x_k in the i-th cluster. The distance between the data x_k and prototype v_i is denoted by ||.||. The fuzzification coefficient m (assuming values greater than 1) quantifies an impact of the membership grades on the individual clusters and implies a certain geometry of the ensuing information granules. Typically, the value of the fuzzification coefficient is set to 2. The partition matrix satisfies two essential and practically justifiable properties

The minimization of Q is completed with respect to U∈U and the prototypes v_i of V={v₁, v₂,...v_c} of the clusters, namely

Here U stands for a family of partition matrices, viz. the matrices satisfying conditions expressed by Eqs. (2) and (3).

From the optimization perspective, there are two individual optimization tasks to be carried out separately to determine the partition matrix and the prototypes. The results are welldocumented in the literature and thoroughly discussed and the method has been intensively experimented with. The optimization process is iterative and involves successive computing of the partition matrix and the prototypes

i = 1, 2, . . . , c; k = 1, 2, . . . , N.

s = 1, 2, . . . , c, t = 1, 2, . . . , n (in the above calculations of the prototypes it has been assumed that the distance function is Euclidean). We can look at the partition matrix by considering its individual rows – denoting them by A₁, A₂, .., A_c we emphasize that fuzzy clustering gives rise to a collection of information granules.

More formally, we can describe this knowledge representation in terms of information granules as a way of expressing any data point x in terms of the information granules and describe the result as a vector in the c-dimensional hypercube, namely [0,1]^c,

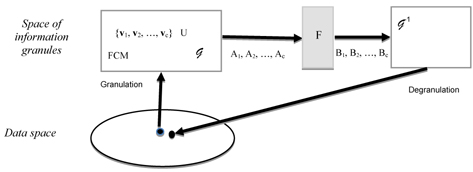
The degranulation step is about a reconstruction of x on a basis of the family of information granules (clusters). It can be treated as a certain mapping

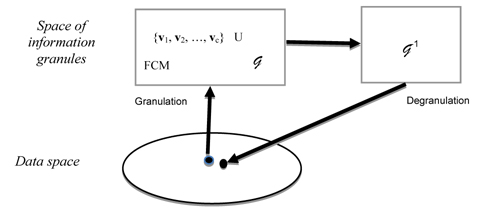
The capabilities of the information granules to reflect the structure of the original data can be conveniently expressed by comparing how much the result of degranulation, say x differs from the original pattern x, that is . More formally, where 𝒢 and 𝒢⁻¹ denote the corresponding phases of information granulation and de-granulation [9].

The crux of the granulation – degranulation principle is visualized in Figure 1 [1]. Note the transformations 𝒢 and 𝒢⁻¹ operate between the spaces of data and the abstract space of information granules.

Let us start with the granulation phase. More specifically, x is expressed in the form of the membership grades u_i of x to the individual granules A_i, which form a solution to the following optimization problem

subject to the usual constraints imposed on the degrees of membership

The solution to the problem (we use here Lagrange multipliers) comes in the form,

For the degranulation phase, given u_i(x) and the prototypes v_i, the vector is considered as a solution to the minimization problem in which we reconstruct (degranulate) original x when using the prototypes and the corresponding membership grades

Considering the use of the Euclidean distance in the above performance index, the subsequent calculations are straightforward yielding the result

It is important to note that the description of x in more abstract fashion realized by means of A_i and being followed by the consecutive degranulation brings about a certain granulation error (which is inevitable given a fact that we move back and forth between different levels of abstraction). While the above formulas pertain to the granulation realized by fuzzy sets, the granulation-degranulation error is also present when dealing with sets (intervals). In this case we are faced with a quantization error, which becomes inevitable when working with A/D (granulation) and D/A (degranulation) conversion mechanisms. The problem formulated above is also associated with vector quantization, which has been widely studied in the literature, cf. [10-14].

The quality of the granulation-degranulation scheme is quantified by means of the following performance index [9]

This performance index articulates how much the reconstruction error is related with the representation capabilities of information granules.

Denoting information granules formed thorough the process of clustering by A₁, A₂, ..A_c we consider a certain framework of interaction among them where such interaction gives rise to the enhancement of the degranulation features and subsequently a reduction of the degranulation error. To highlight the essence of the approach, we can refer to Figure 2.

The essence of this enhanced mechanism dwells on a mapping (transformation) F: {A₁, A₂,.., A_c}→ {B₁, B₂. ,. . . , B_c} where B_i= F(A₁, A₂, . . . , A_c). The original membership functions are affected by their interaction with other information granules. The newly formed granules are developed in a way it furnishes them with better degranulation capabilities (viz. lower degranulation error).

In general, the transformation F: [0,1]_c →[0,1]_c can be implemented in numerous ways. Several interesting and practically viable alternatives are summarized in Table 1. The same table includes some comments about the nature of the mapping.

The transformation F is typically endowed with some parameters (say a matrix of weights) and those imply the flexibility of the transformation. Both the type of the mapping as well as its parameters (their numeric values) are subject to the optimization guided by the degranulation error V. More formally, we can describe the result of this optimization as follows

where F_opt is an optimal transformation (coming out of a finite family of alternatives) whereas w_opt is an optimized vector of its parameters. The minimization shown in Eq. (15) is realized with regard to the type of the transformation F and its parameters w.

As to the development of interactions, a certain general tendency can be observed. Consider a linear combination of original information granules shown in Table 1. Let us rewrite it in the following form

We note that B_i is a distorted (transformed) version of A_i in which in an attempt to minimize the degranulation error the original information granule A_i is impacted by the membership grades of the remaining A_j s. Depending upon the sign of the weights, this process is of excitatory (w_ij >0) or inhibitory (w_ij <0) nature. In other words, those A_js associated with the negative weights w_ij form an inhibitory link while the excitatory link is realized by the A_jcoming with the positive entries of W. A lack of interaction is observed when w_ij are close to zero for all i ≠j or W = I where I is an identity matrix. While more sophisticated transformation may contribute to the lower degranulation error, the interpretability of the transformation itself could be more difficult because of the existence of more nonlinear and convoluted character of established interactions among information granules.

In all experiments, we consider the linear transformation of information granules (Table 1). Particle swarm optimization is used as an optimization vehicle [15]. We consider a generic version of this method where the dynamics (velocity and position) of each individual of the swarm of “M” particles is governed by the following expressions:

i = 1, 2, . . . , M and j = 1, 2, . . . , r. Here v_i is the velocity of the i-th particle in a given search space of dimensionality “r” and r₁ and r₂ are the vectors of random numbers drawn from the uniform distribution over the unit interval. p_i is the best position of the i-th particle observed so far and pg is the best particle in the entire swarm. The update of the particle is realized by adding the velocity v_i(iter+1) to the current position x_i(iter). The main parameters of this optimization environment is set as follows (these specific numeric values are those commonly encountered in the literature): c₁=c₂=1.49, w = 0.6. The range of the admissible values of the weights is set to [−4, 4].

The size of the population was set to 120 individuals whereas the number of generations was equal to 100. With regard to the use of the FCM algorithm, the fuzzification coefficient is set 2 and the method was run for 60 iterations (at which point no changes to the values of the objective function were reported). The initial point of optimization was set up randomly by choosing a partition matrix with random entries. The distance function used to run FCM as well as to compute the degranulation error Eq. (14), is the weighted Euclidean distance in the form where s_j stands for a standard deviation of the j-th variable.

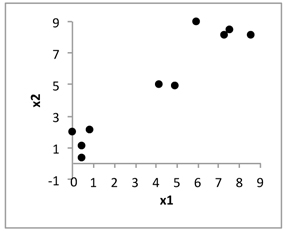
We start with a synthetic two-dimensional data with intent of gaining a better insight into the nature of the optimization process and the produced results. The data set exhibits three welldelineated and compact clusters (groups), Figure 3.

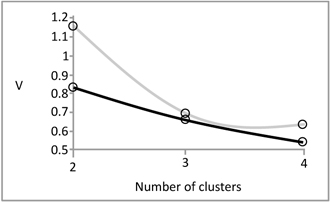
We formed c = 2, 3, and 4 information granules (fuzzy clusters) and determined the resulting degranulation error for all these situations, see Figure 4.

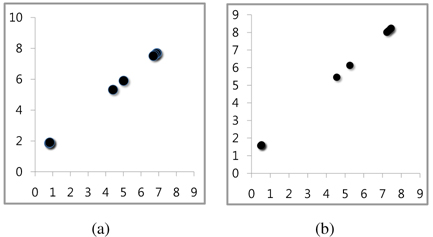
The most visible improvement is noted for c = 2. Just to observe in which way the reduced value of V translates into the character of the reconstructed data, Figure 5 contrasts the results obtained when no associations among information granules were considered. It is apparent that in this case a number of data were collapsed whereas the inclusion of the associations help retain the original data as it is visible in Figure 5(b), especially with regard to the cluster of data positioned close to the origin.

The matrix of the parameters W delivers a detailed insight into the relationships among information granules. Here we have

The relationships (associations) between information granules are more visible with the increase of the number of clusters with both inhibitory and excitatory linkages being present.

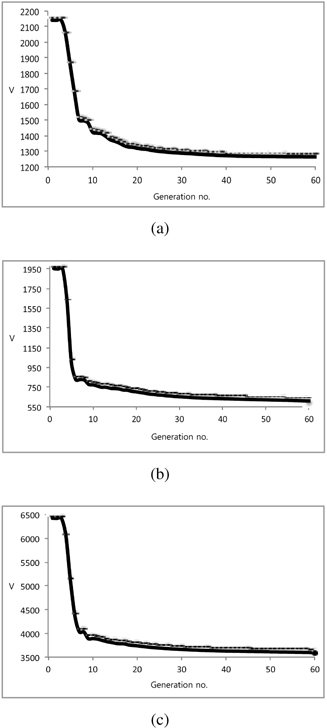
A collection of three data sets coming from the Machine Learning repository http://archive.ics.uci.edu/ml/ is considered, namely e-coli, auto, and housing. The snapshots of the progression of the optimization process where the fitness function (degranulation error) is reported in successive generations are presented in Figure 6.

The plots of V treated as a function of the number of clusters are displayed in a series of figures, Figure 7.

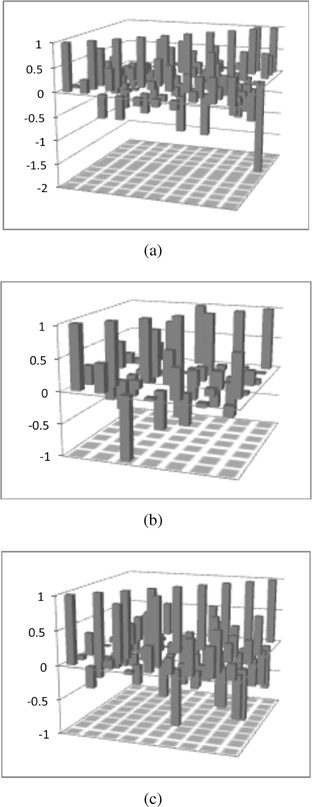
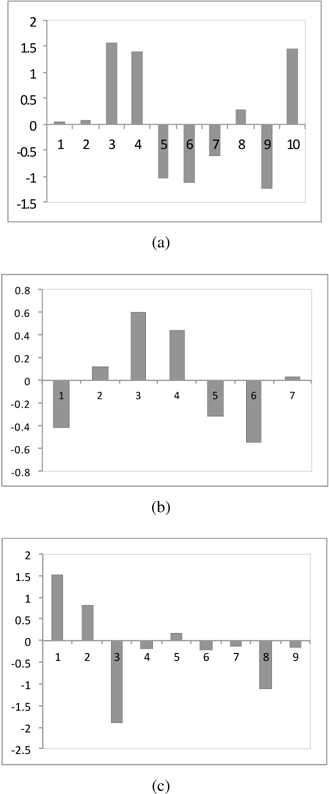
In all experiments, there is a visible improvement provided by invoking associations among information granules. This enhancement is quite steady irrespectively from the number of clusters used in the granulation process. We also witness a saturation effect meaning that the values of V tend to stabilize with the increase of the number of clusters. The plots displayed in Figure 8 deliver a certain look at the values of the weights; the diversity of the inhibitory and excitatory effects delivered by their combination is also apparent. A more global view can be formed by considering a sum of the weights reported in the individual rows of the weight matrix (not counting the entries positioned on a main diagonal) – these numbers tell us about an overall impact on the corresponding fuzzy set that arose as a result of the transformation. As illustrated in Figure 9, there is a visible diversity of excitatory and inhibitory influences among information granules.

Understanding and quantifying information granules in terms of their representation capabilities is essential to further advancements of granular computing and pursuing their role in reasoning and modeling schemes. The study covered here underlines a facet of degranulation aspects and its improvement by admitting and quantifying linkages existing among information granules. This helps gain a better insight into the nature and interaction among information granules built on a basis of numeric data. In the numeric studies reported in the paper, we stressed an important role of associations of fuzzy sets. While in this study we focused on the formalism of fuzzy sets (and fuzzy clustering), the developed framework is of general character and as such can be investigated in depth when dealing with other formalisms of information granules (sets, rough sets, shadowed sets and others).

No potential conflict of interest relevant to this article was reported.