The problem of wave scattering by particles is one of the fundamental subjects in physics, with a very long history, and we can find quite a long list of articles dealing with it [1-8]. The articles can be divided by subject into two classes: single scattering and multiple scattering. The criterion of this classification is not the number of scattering particles in the medium, but how close the particles are, and how strongly they scatter the wave. Even in the presence of many particles, if they are dispersed tenuously in space such that the wave scattered by one particle becomes very weak compared to the incident wave when it comes to other particles, multiple scattering effects can be safely ignored.

For problems of a single particle scattering, we have analytical solutions for particles whose shape is simple and symmetric: an infinite plane is a textbook example, as are a circular cylinder [9], a spherical particle [10 11], and a spheroid [12]. For problems of multiple particle scattering, analytic solutions are rare, except for very simple shapes: two parallel infinite planes (corresponding to the Fabry-Perot interferometer) is another textbook example, as are coaxial cylinders [13], concentric spheres [14], two parallel cylinders [15 16], and two spheres [17]. However, even the apparently simple problem of a plane wave scattered by a sphere or cylinder situated near a planar substrate has not yet been completely solved to give rigorous analytic solutions, and thus various approximation methods have been proposed [18-25].

Multiple scattering is in essence a succession of single scatterings in time: a wave scattered by a particle propagates to another particle and is scattered again, and this process can repeat indefinitely. Therefore, such a feature should be reflected in a properly developed theory of multiple scattering. However, we still do not yet have an appropriate general framework for an analytical theory of multiple scattering which reveals such a feature. In this article we would like to address the fundamentals of multiple scattering by considering the scattering of a wave by two particles. As we want to see the essential features of the theoretical framework of multiple scattering, emphasis will be put on the mathematical structure, rather than on getting the analytic solution to a specific scattering problem.

Considering the relative positions of two particles, there can be three configurations: 1) two particles are separated without any overlap, except for possible contact at a point or along a curve; 2) a composite particle, in which one particle is completely buried within the other particle; or 3) two particles partially overlap, in contact with each other over a surface of finite area. In this article we analyze the first configuration of two completely separated particles. The second configuration will be analyzed in the future. Analysis of the third configuration might be interesting and of practical importance [7] but seems to lead to excessively complicated results,so we do not attempt it.

For simplicity and clarity of mathematics, we analyze the problem of scalar wave scattering by two separated particles. Although it is necessary to use a full vector wave theory to analyze the problem of electromagnetic wave scattering, the result would be rather complicated, and we do not pursue it here. Furthermore, the essential features of the results should be similar for both scalar and vector waves, and the result obtained in this article could be extended to the scattering of a vector wave by two particles.

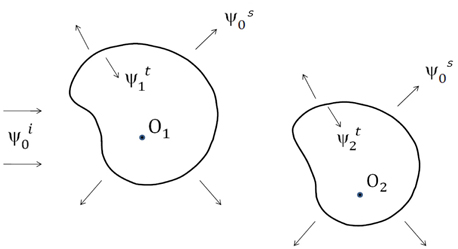
Figure 1 shows the general situation of the problem: two particles labeled 1 and 2, with refractive indices N₁ and N₂ respectively, are located with their centers at O₁ and O₂ within the background medium of refractive index N₀, the value of which is taken to be 1 for simplicity.

In this situation a monochromatic scalar wave of angular frequency ω is incident on and scattered by the two particles. Suppressing the common time harmonic factor e^-iωt, we can express the spatially dependent part of the wave function in the background medium and within the two particles in the following way:

Here is the incident wave, is the wave scattered by the two particles, and and are the waves transmitted into particles 1 and 2 respectively. These wave functions satisfy the following Helmholtz equations:

where K₀ is the propagation constant of the wave in the background medium and is related to the velocity c and the angular frequency ω of the wave in the following way: K₀ = ω/c . The wave function should also satisfy the boundary condition that demands continuity of as well as its normal derivative at the surfaces 𝜕₁ and 𝜕₂ of particles 1 and 2.

The problem at hand is to find the wave function that satisfies Eqs. (1) and (2) with appropriate boundary conditions when the wave function of the incident wave is specified.

The first step is to expand the wave function in terms of the eigenmodes of the two particles. Suppose the eigenmode solutions of the Helmholtz equations in the background medium and within particle 1, in the coordinate system with its origin at O₁, are and . Similarly, and are the eigenmode solutions of the Helmholtz equations in the background medium and within particle 2 in the coordinate system with its origin at O₂. The subscripts n and v denote the mode indices. The possible value of a mode index depends on the shape of the particle. For example, for a sphere the index would be a pair of integers {l, m}. However, to avoid notational complexity, a single character is used for designating the mode index here. These eigenmodes form complete orthogonal bases where they are defined:

The wave function of the incident wave can be expanded either in terms of the eigenmodes {} of particle 1 or the eigenmodes {} of particle 2 in the following form:

The wave function of the scattered wave can also be expanded in a similar way, but as we have two independent particles 1 and 2, the form is somewhat different:

Here {} and {} are the eigenmodes of particles 1 and 2 whose asymptotic forms are outgoing waves.

Since {} and {} are complete orthogonal bases, each can be expressed as a linear combination of the other in the following way:

where and are eigenmodes of particles 1 and 2 whose asymptotic forms are incoming waves converging respectively to particles 1 and 2.

We can rewrite Eq. (1) by using the bases in the following way:

Here s_n and t_n are the scattering and transmission coefficients of the nth eigenmode of particle 1, which are defined as the expansion coefficients of the scattered and transmitted waves, when the eigenmode is incident. and are similarly defined, but for particle 2.

Now convert the boundary conditions demanding that wave function and its normal derivative be continuous on the surfaces of particles 1 and 2 into the equations of s_n and t_n, and of and .

The equations of continuity for and on the surface of particle 1 are the following:

Here (1) denotes a position on the surface of particle 1. Using Eq. (6b), Eqs. (8a) and (8b) can be rewritten in the following form:

Since is the normal derivative of , its angular function remains the same. As the orthogonality relation, Eq. (3a) comes from angular integration, and if we apply it to Eqs. (9a) and (9b) we get the following equations:

s_n and t_n can be obtained by solving these coupled linear equations:

Here and are the scattering and transmission coefficients of particle 1 when it is alone in the background medium and receives eigenmode as the incident wave:

Similarly, and are the scattering and transmission coefficients of particle 1 when it is alone in the background medium in the absence of particle 2 and receives eigenmode as the incident wave:

On the surface of particle 2 the continuity equations for and are the following:

Here (2) denotes a position on the surface of particle 2. By using Eq. (6a), Eqs. (14a) and (14b) can be rewritten in the following form:

As in the previous case, if we apply the orthogonality relations Eq. (3b) to Eqs. (15a) and (15b) we get the following equations:

and can be obtained by solving these coupled linear equations:

Here, and are the scattering and transmission coefficients of particle 2 when it is alone in the background medium and receives eigenmode as the incident wave:

Similarly, and are the scattering and transmission coefficients of particle 2 when it is alone in the background medium and receives eigenmode as the incident wave:

Eqs. (11a-b) and (17a-b) are the expressions for the scattering and transmission coefficients s_n and t_n of particle 1 and and of particle 2. However, as the two sets of expressions are coupled, we have to go one step further to separate them. For the scattering coefficient s_n, we substitute Eq. (17a) for in Eq. (11a), and after rearranging the expression, we get the following recurrence formula:

On the right-hand side, the first term is the wave directly scattered by particle 1. In the second term, the first term in the square brackets is, among the wave scattered by particle 2 ( α_ν), an eigenmode that comes to particle 1and is then scattered by it (). The second term is the component that is converted into the outgoing wave from particle 1 as the mode (). The third term comes from the wave of mth mode scattered by particle 1 (a_ms_m), and it breaks into two terms in the square bracket The first is a part converted into the mode convergent to particle 2 and then scattered by it (), and after that a part of it is converted into , a mode converging to particle 1, and then scattered again (), and the other part is converted into , a diverging mode from particle 1. The second is a part converted into mode diverging from particle 2, which is then decomposed into the two components as explained above.

For the transmission coefficient t_n, we substitute Eq. (17a) for in Eq. (11b), and we get the following recurrence formula:

The first term on the right-hand side is the transmission coefficient of particle 1 when it is alone. The second term comes from the part of the wave scattered by particle 2, converted into , a mode converging to particle 1, and then transmitted into it (). The third term comes from the mode scattered by particle 1 at first (s_ma_m), after which a part of it is converted into a mode converging to particle 2 and then scattered and coming to particle 1 again. The other part is converted into a mode diverging from the particle and also coming to particle 1 again. Both components are decomposed as various modes converging to particle 1 () and then parts of them are transmitted ().

Similarly substituting Eq. (11a) for s_n in Eqs. (17a) and (17b), we get the following recurrence formulae for and :

Interpretation of the terms in the formulae above is quite similar to that of Eqs. (20a) and (20b).

We have derived a general form of the analytical solution of the problem of scalar wave scattering by two separated particles. The scattered and transmitted waves are expressed as a linear combination of eigenmodes of the two particles. The strength of each eigenmode is determined by the coefficients of scattering and transmission of the eigenmode by each particle. Formulae for these coefficients are expressed in the form of linear recurrence relations. Iterative application of the recurrent formulae gives the coefficients in power-series form, in which each term can be interpreted as successive repetition of scattering by the two particles, with appropriate phase delay and reduction in amplitude for each scattering event.

The solution obtained can be applied to some simple problems which were already solvedapproximately [17-25], to provide more detailed and accurate solutions. Although the theory we have developed here deals with the problem of scattering by two particles, it can be extended to the situation of more particles [26-30].