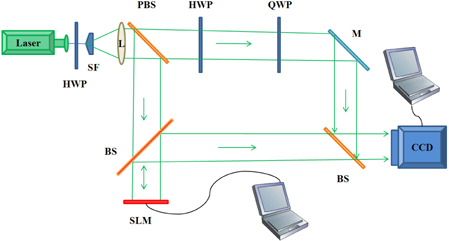
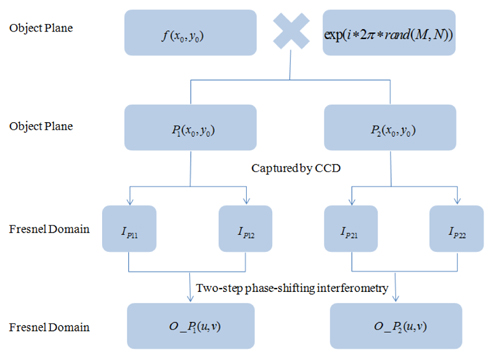
We propose a split-encryption scheme on converting original images to multiple ciphertexts. This conversion introduces one random phase-only function (POF) to influence phase distribution of the preliminary ciphertexts. In the encryption process, the original image is mathematically split into two POFs. Then, they are modulated on a spatial light modulator one after another. And subsequently two final ciphertexts are generated by utilizing two-step phase-shifting interferometry. In the decryption process, a high-quality reconstructed image with relative error RE = 7.6061-31 can be achieved only when the summation of the two ciphertexts is Fresnel-transformed to the reconstructed plane. During the verification process, any silhouette information was invisible in the two reconstructed images from different single ciphertexts. Both of the two single REs are more than 0.6, which is better than in previous research. Moreover, this proposed scheme works well with gray images.
With the development of computer calculations and network connections, more and more threats and attacks are generated in information communication systems. Optical information security has attracted a lot of attention, which offers primarily two types of benefits; the first is an inherent capability for parallel and rapid processing, and the second is a concealment in any of several dimensions, such as phase or spatial frequency [1]. Optical systems have an excellent capability to encode information. In general, there are three main classes of cryptography for implementing optical image encryption. The first is encrypting an image to one stationary white noise-like ciphertext utilizing an encryption key. The second is multiple-image encryption (MIE) which encrypts multiple images to one ciphertext by taking advantage of different encryption keys. The double random phase encoding (DRPE) method and the iterative phase-retrieval algorithm are extensively utilized in both of those encryption methods. In this paper we call the third one (encrypting one image into multiple ciphertexts) splitencryption (SE) for simplicity.
Encryption utilizing the DRPE method includes both symmetric and asymmetric cryptographic algorithms because the decryption key could be identical to or the conjugate with the encryption key. Two random phase-only functions (POFs) are utilized in this method. The first POF improves the signal of a charge-coupled device (CCD), and the second POF is the encryption key in the system [2]. However, when the complex conjugate of the information obtained in the frequency domain is considered as the ciphertext, the decryption key must be identical to the second random POF so-called symmetric cryptography. When the information obtained in the frequency domain is considered as the ciphertext, the decryption key has to be the conjugate of the second random POF-asymmetric cryptography. Indeed, the DRPE method is used in different interferometries and transforms to implement optical information security. Refregier and Javidi first suggested the DRPE method [3] that has been exhaustively developed in recent decades. As phase-shifting interferometry is developed, Lee and Gil applied the DRPE method to four-step phaseshifting interferometry for implementing optical encryption [4]. Shen
MIE encrypts several images into one single ciphertext. This encryption technique can hide more information, so it is more complicated. Meanwhile, most algorithms are timeconsuming. The biggest problem is crosstalk, which means how to reconstruct every single image in high quality from the only one single ciphertext. Because of this, MIE is more suitable for binary images than gray images. Shi
Optical image split-encryption has been growing rapidly since Zhang and Wang suggested it for the first time [15]. The authors modulated the optical field in the Fresnel domain to two phase-only masks (POMs) to be allocated to two authorized users. In the decryption processing, if and only if the authorized users get together, the reconstructed image can be obtained by an inverse Fresnel transform. Unlike DRPE, the SE scheme does not need an explicit key for the ciphertext. In the SE scheme, one ciphertext also plays a role of the key of another ciphertext. Similarly, unlike MIE, the SE scheme does not introduce any time-consuming iterative phase-retrieval methods. Therefore, the SE scheme is more efficient and more convenient to manipulate. But there is a serious silhouette problem in the SE scheme. The silhouette information of the original image is visible (when reconstructed) in both of the two POMs. Addressing this issue, Wang and Zhao introduced a third random POM for effectively eliminating the silhouette problem [16], but this scheme only focused on removing the silhouette problem when reconstructing a single POM. If the product of two specific POMs is reconstructed, the silhouette information will become visible. Kumar
In this paper, we propose an optical image split-encryption scheme to overcome the flaws enumerated in all the papers above. During the encryption process, the original image uses a random phase-only function introduced to influence phase distribution of the preliminary ciphertexts. Then we obtain a new complex original image and convert it to two phase-only functions that are the preliminary ciphertexts. Next, the optical fields of these two phaseonly functions can be obtained by taking advantage of a two-step phase-shifting method. These two encrypted optical fields cooperate with each other to reconstruct the original image. This proposed scheme requires no extra iterative algorithms, chaotic algorithms and random POMs in the Fresnel domain. It can be applied not only to a binary image but also to a gray image. The most important characteristic is utilizing only two ciphertexts to completely eliminate the silhouette problem.
The principles of the proposed optical image splitencryption are introduced in Section 2. In Section 3, computer simulation is described to demonstrate the feasibility of the proposed SE scheme. Error analysis is described in Section 4. Concluding comments are shown in Section 5.
II. PRINCIPLES OF THE PROPOSED OPTICAL IMAGE SPLIT-ENCRYPTION
Fresnel transforms are based on Fourier transforms, and Fourier transforms obey the distributive law, so Fresnel transforms also obey the distributive law. This induces the proposed encryption scheme, whereby
where
where
The ideal encryption system can approach both encryption and decryption manipulations in an optical manner, but just one process could be implemented optically. Most researchers investigate decryption optically owing to restrictions such as component limitations and difficulty in optical setup configuration, etc. We adopt optical encryption to obtain the final ciphertexts
The mathematical expressions of the encryption process are described as follows:
where
Here, the optical fields
where
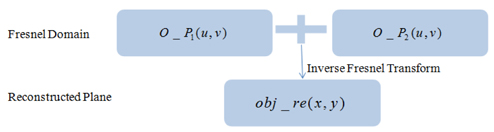
The decryption flow chart represented in Eq. (15) is depicted in Fig. 3.
The feasibility of the proposed scheme was verified with a 256× 256 grayscale Baboon image (Fig. 4). The phase portions of the two POFs are depicted in Fig. 5(a) and Fig. 6(a), respectively.
No silhouette information of the original image can be seen in Fig. 5(c), which is the reconstructed image generated from
Relative error (
where
The
For comparison, the method of Wang and Zhao [16] was simulated again for this paper. Some of the results are shown in Fig. 8.
They introduced a random POF to split the complex amplitude of the optical field into POF1, POF2 and POF3; the
A digital hologram recorded on a CCD is quantized with 256 levels. So a gray-level error on CCD camera pixels can be generated due to a small intensity variation, which is the so-called quantization error [2]. If there is no error, the decryption equation expression should be like Eq. (7), Eq. (11) and Eq. (15). However, the error appears when the CCD camera captures the optical field
Where
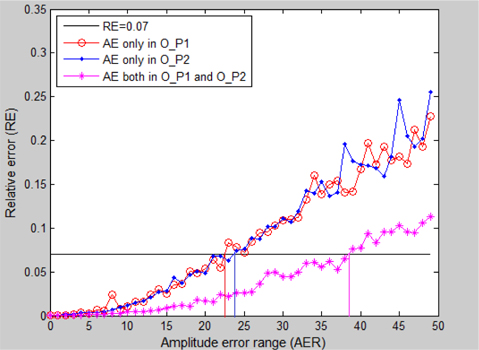
The purpose of the error analysis is to calculate what amplitude error range (AER) and phase error range (PER) the reconstructed image can tolerate for the naked eye. First, a toleration criterion should be determined. The different
All of the images depicted in Fig. 9 are the reconstructed images from the optical fields with amplitude errors or phase errors, or both. For example, the
The results in Fig. 10 are similar to those in Fig. 9. The noise is acceptable to the naked eye from Fig. 10(a) to (f). However, the noise increases suddenly between Fig. 10(g) and (h), as seen in the nose of the Baboon images. Therefore,
Here, the Lena and Baboon images are both utilized to analyze the AER and PER with
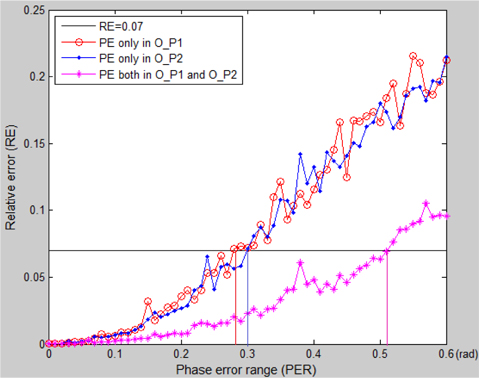
In Fig. 11, the full black line represents the threshold line
In Fig. 12, the full black line represents the threshold line
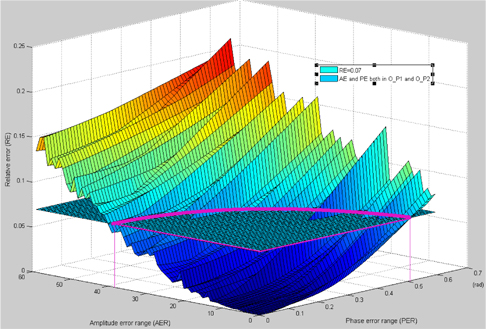
In Fig. 13, the plane represents the threshold plane
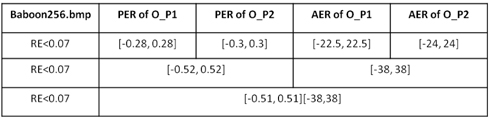
The data in Table 1 illustrate Fig. 11, Fig. 12, and Fig. 13. It is worthwhile to note that the maximum AER and PER are taken from Fig. 13, assuming there is no influence from other different categories of errors. In these three figures, the last point not exceeding the black line is taken into account. In addition, although the RE curves increase tortuously as AER or PER expands, the shapes of the curves rise steadily in the long term.
[TABLE 1.] Tolerated AER and PER of the 256×256 grayscale Baboon image
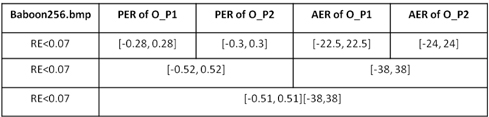
Tolerated AER and PER of the 256×256 grayscale Baboon image
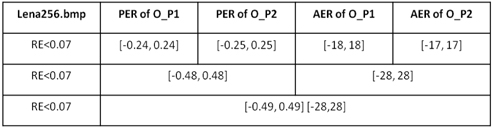
We conducted the same process with the Lena image, and the results are depicted in Table 2. According to Table 1, Table 2 and other data not listed in this paper, different images have different tolerated PERs and AERs. However, if both of the phase errors of the optical field work together, the tolerated PER will increase to almost twice that seen when PE happens in a single optical field. If both of the amplitude errors (AEs) of the optical field work together, the tolerated AER will increase to almost twice when AE happens in single ciphertext. It means the PE in
[TABLE 2.] Tolerated PER and AER of the 256× 256 grayscale image of Lena
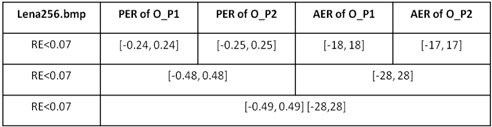
Tolerated PER and AER of the 256× 256 grayscale image of Lena
The proposed optical image split-encryption scheme focuses on the optical information encryption for converting original plaintext to multiple ciphertexts. It requires no complicated iterative algorithms or chaotic transforms. Moreover, fewer phase-only functions need to be split. It can be applied to gray images, and introduces only one random POF for influencing subsequent encryption. The encryption procedure is to split the original image into two POFs mathematically, subsequently obtain two authorized ciphertexts generated from those two POFs by taking advantage of a two-step phase-shifting method. The original image can be reconstructed with an extremely small relative error